人工磁導體結構組成間隙波導的理論仿真研究
方超,逯貴禎
(中國傳媒大學 信息工程學院,北京 100024)
1 引言
在毫米波傳輸技術的研究中,為了降低電磁波在傳統波導中傳播時的損耗,一種基于超材料人工磁導體結構的新型波導傳輸結構被提出。這種新型的波導傳輸結構如圖1所示。
該結構的英文名字為“gap waveguide”,中文名字多稱為“縫隙波導”,為了與“波導縫隙天線”區分,建議命名為“間隙波導”。
間隙波導的下層由兩邊的周期金屬針床結構和中間的金屬脊組成,間隙波導的上層是金屬板。間隙波導的橫截面示意圖如圖2所示。
電磁波被束縛在PEC-PEC(理想電導體)的區域中向前傳播,而在PEC-HIS(高阻表面)區域中電磁波被抑制。與傳統的矩形波導相比,間隙波導中傳播的是TEM波,沒有截止頻率,并且由于少了側面的兩個金屬表面,理論上間隙波導應該比傳統金屬矩形波導的傳輸損耗小。圖2中形成HIS的周期金屬針床結構又被稱為AMC(人工磁導體),可以用來替代間隙波導理論模型中的PMC結構[1],當金屬導體和人工磁導體表面間距小于1/4波長時,電磁波無法傳播。

圖2 間隙波導橫截面示意圖
國內對間隙波導結構的研究相對較少,國外研究間隙波導結構的主要有Chalmers University of Technology的Per-Simon Kildal教授團隊。該團隊在2009年提出了一種寬帶,低損耗,能夠傳輸TEM模式電磁波的間隙波導[2] [3],隨后對間隙波導的研究主要集中在結構改進的方面。文獻[4]提出了一種基于蘑菇形狀周期結構的間隙波導,文獻[5] [6]將金屬針變成了彈簧和兩個對接的到梯形,主要目的就是為了縮短金屬針的長度,減小間隙波導的體積。文獻[7]還在間隙波導結構的基礎上提出了對應的諧振器結構。
2 平行周期金屬線結構的色散方程
間隙波導傳輸線結構最核心、最基本的組成部分就是平行金屬線組成的周期結構,如圖3所示:

圖3 平行周期金屬線結構
這種結構在宏觀上構成的媒質就屬于電磁超材料的一種,也是最早被提出的一種電磁超材料形式。該結構在微波領域的應用有很多,例如天線的反射器、人工阻抗表面等。對于平行周期金屬線結構的電磁特性理論研究有很多數值方法。但是在精確建模上進展甚微。基于傳輸線理論的方法只有在金屬線間隔足夠大的情況下才有準確結果[8],直到2002年,P.A.Belov提出了一種簡便又能準確描述平行周期金屬線結構色散特性的方法[9],并且給出了色散方程:
(1)
該色散方程在金屬線半徑遠小于周期間隔尺寸和工作波長時非常準確。這個色散方程的數值結果表明電磁波在所有垂直于金屬線表面的傳播方向上都存在一個低頻的禁帶。當a?π/k時,用泰勒級數展開和sin(x),色cos(x)散方程可以簡化為:
(2)
其中,
(3)
公式2中的kp表示等離子頻率對應的波數,更準確的說,它代表禁帶的上邊界。公式2可以類比于傳統等離子頻率的表達式,對于平行周期金屬線結構該表達式更加準確,并且表明結果更依賴于平行周期金屬線結構的物理尺寸。
3 人工磁導體中的傳播模式
組成間隙波導傳輸線結構的第一步是將平行周期金屬線固定在金屬平板上形成人工磁導體結構(AMC),如圖4所示:
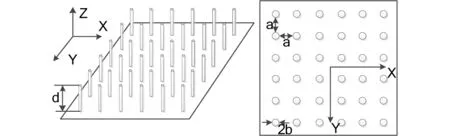
圖4 人工磁導體結構
金屬線高為d,半徑為b,橫向和縱向的周期間隔為a。則結構的介電常數為張量,可以用公式4表示:
(4)
其中,
(5)
而k代表主媒質中的波數,
(6)
kp是上一節提到的等離子體波數,只依賴于結構的尺寸,即周期間隔和金屬絲半徑。
在AMC結構中TM波的反射系數為:
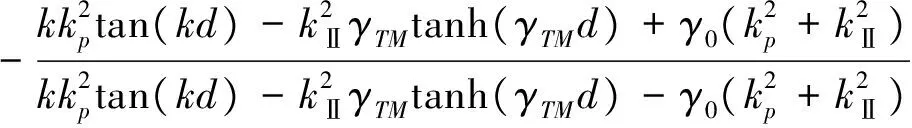
(7)

公式7中的反射系數是通過主媒質中TM波的衰減系數γTM來表示的,當平行金屬線足夠密集時,即當a/b?1,b/a為常數時,γTM→kp→1/a→∞。kz是由平面波的入射方向決定的。對于TE波,反射系數只和平面金屬板有關,因為TE波垂直于金屬線,所以平行金屬線結構對TE波沒有影響,則TE波的反射系數為:
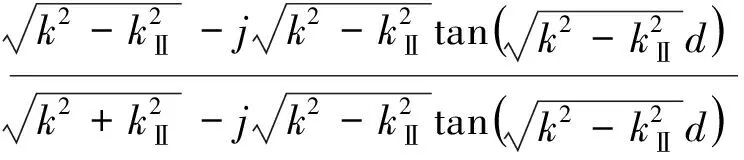
(8)
當金屬線足夠密集時,

(9)
當只考慮TEM模式時,反射系數也可以用公式9來表示。
因此,當平行金屬線足夠密集時,媒質為各項異性材料,εxx=εyy=1,εzz=∞,媒質的等效阻抗為:
Zs=jξtan(kd)
(10)
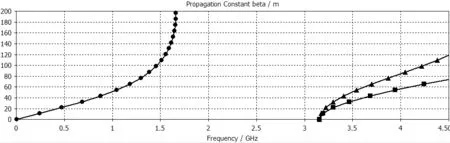
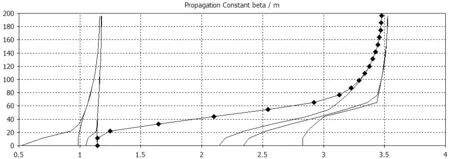
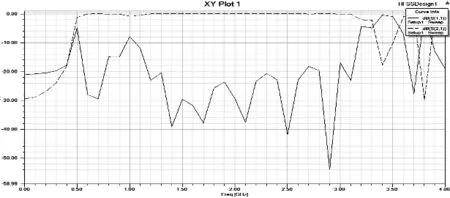
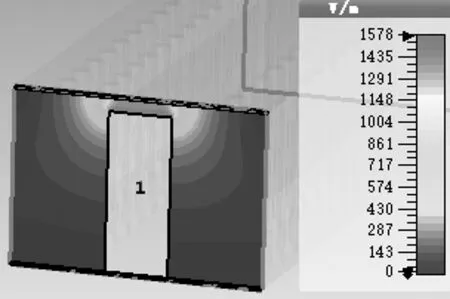
當d≤λ/4時,媒質的阻抗為感性;當λ/4 在上一節所介紹的人工磁導體上間隔一段距離覆蓋與之平行的金屬板如圖5: 圖5 AMC-PEC結構 金屬線的高度為d,周期金屬柱的上方覆蓋金屬板,與金屬柱結構相距h。覆蓋金屬板后的形成的AMC-PEC結構中的場分布比沒有覆蓋金屬板的結構要更加復雜,電磁波在限定空間內傳播特性也可以用ΓTM(kz)和ΓTE(kz)來描述。由結構可知,上邊界為PEC,切向電場為0,即: [ejkzz+ΓTM,TE(kz)e-jkzz]z=h=0 (11) 對于TE波而言,波的傳播模式只取決于上下金屬板,即上下兩個PEC邊界條件,故: kz=π/(h+d) (12) 對于TM波而言,由公式7和11可得: (13) 將公式13類比于電路諧振方程: (14) 由此可以得出AMC-PEC結構的等效電路圖如圖6所示[10]: 圖6 AMC-PEC結構等效電路圖 (15) 即: (16) 其中虛線表示TM模式的波,實線表示TE模式的波,結果都能夠看出在1.2GHz-2.3GHz有一個明顯的禁帶,表明這個頻段內的電磁波不能在該結構中傳播,給利用AMC-PEC結構制作間隙波導提供了理論基礎。 圖7 AMC-PEC結構色散曲線 首先對AMC-PEC結構的色散曲線進行仿真,建立如圖8所示的一個周期結構,h=5mm,a=8mm,b=4mm: 圖8 AMC-PEC結構單個周期仿真模型 可以得到AMC-PEC結構的色散曲線。 由圖9-圖11可以看出d取不同的值,直接影響禁帶的帶寬,而且禁帶的下限滿足d=λ/4的關系。當h=60mm時,仿真結果和數值計算結果匹配得很好。 然后,對間隙波導結構的散射曲線進行仿真,可以利用周期結構仿真模塊對如圖12所示的一個周期進行仿真,參數設為h=5mm,d=60mm,a=8mm,b=4mm: 得到色散曲線如圖13所示。 可以看出在AMC-PEC結構1.2-2.2GHz的禁帶中出現了一個新的傳播模式,是間隙波導中的準TEM波。 最后,為了證明間隙波導的可行性,分別用了CST和HFSS對間隙波導的S參數和電磁場分布進行了仿真,得到的結果如圖14-16所示。 圖9 d=40mm時 圖10 d=60mm時 圖11 d=80mm時 圖12 間隙波導單個周期仿真模型 圖13 間隙波導色散曲線 圖14 CST仿真S參數(實線S11、虛線S21) 圖15 HFSS仿真S參數(實線S11、虛線S21) 圖16 電場分布示意圖 圖14和圖15分別用HFSS和CST對間隙波導的S參數進行了仿真,可以看出兩個結果在1G-3G頻段有相同的趨勢,S11和S21滿足波導傳輸的要求,兩種軟件的結果相互驗證,證明了間隙波導的可行性。需要強調的是,由于CST采用的是時域的方法,能夠迅速得到結果,而用HFSS仿真的過程則非常緩慢。圖16是間隙波導的電場分布示意圖,可以明顯看出間隙波導中的電場被束縛在中間的脊區域,這也和理論相符。 [1]逯貴禎,洪楚雨,方超.金屬條帶縫隙波導結構特性研究[J].微波學報,2014(2):184-186. [2]Kildal P S,et al.Wideband,Low loss,Low-cost,Quasi-TEM Metamaterial-based Local Waveguides in Air Gaps Between Parallel Metal Plates[C].International Conference on Electromagnetics in Advanced Applications,Torino,Italy,2009:588-591. [3]Kildal P S,et al.Local Metamaterial Based Waveguides in Gaps Between Parallel Metal Plates[J].IEEE Antennas and Wireless Propagation Letters,2009,8(4):84-87. [4]Pucci E,Kildal P S,et al.New Microstrip Gap Waveguide on Mushroom Type EBG for Packaging of Microwave Components[J].IEEE Microwave and Wireless Components Letters,2012,22(3):129-131. [5]Iglesias E R,Kildal P S,et al.Bed of Springs for Packaging of Microstrip Circuits in the Microwave Frequency Range[J].IEEE Transactions on Components,Packaging and Manufacturing Technology,2012,2(10):1623- 1628. [6]Shams S I,Kishk A A,et al.Double Cone Ultra Wide band Unit Cell in Ridge Gap Waveguides[C].Antennas & Propagation Society International Symposium,Memphis,Tennessee,USA,2014:1768- 1769. [7]Pucci E,Zaman A U,et al.Study of Q-factors of ridge and groove gap waveguide resonators[J].IET Microwaves,Antennas& Propagation,2013,7(11):900-908. [8]Nicorovichi N A,McPhedran R C,et al,Photonic band gaps for arrays of perfectly conducting cylinders[J].Physical Review E,1995,52(1):1135-1145. [9]Belov P A,Marques R,et al.Strong spatial dispersion in wire media in the very large wavelength limit[J].Physical Review B,2003,67(11):621-623. [10]Polemi A,Maci S,et al.Dispersion Characteristics of a Metamaterial-Based Parallel-Plate Ridge Gap Waveguide Realized by Bed of Nails[J].IEEE Transactions on Antennas and Propagation,2011,59(3):904- 913.4 AMC-PEC結構的色散分析

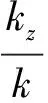


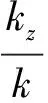


5 間隙波導結構的仿真分析