立體幾何解題策略的再探究
朱小扣 周 園
(1.安徽省無為縣牛埠中學 238351;2.安徽省舒城縣萬佛湖鎮中心學校 231360)
立體幾何題是高考的重要考點之一,每年高考題中都會出現,約為20分左右.而學生在解答中,容易失誤失分,經常會出現“會兒不對,對而不全”的現象,為此筆者現對其答題策略做如下探討.
一、補形法
補形法雖類似于三視圖中的模型法,但用法有區別,補形法更注重局部和整體的聯系,特別是在做立體幾何的大題時,不補形的話,猶如在“云里霧里”,有時補形后,答案一目了然.

(Ⅰ)試確定點M的位置,使AC∥平面MDF,并說明理由;
(Ⅱ)在(Ⅰ)的條件下,求平面MDF將幾何體ADE—BCF分成的較小部分與較大部
分的體積比.

圖1
解析(Ⅰ)當M是線段AE的中點時,AC∥平面MDF,證明如下:
連結CE交DF于N,連結MN.由于M、N分別是AE、CE的中點,所以MN∥AC.
所以AC∥平面MDF.

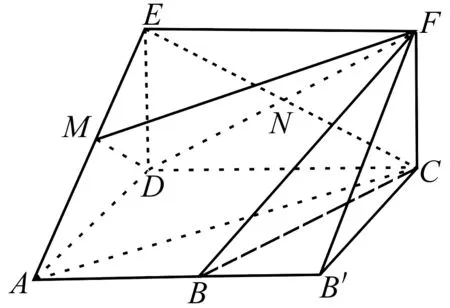
圖2
二、顛倒法
在數學解題中經常會要求變換角度,顛倒法就是其中一種,通過顛倒可以將不熟悉的圖形轉化成熟悉的圖形,這是對知識能力的深度考察.雖然顛倒法簡單,但絕不應被忽視.
例2 (2016山東理17改編)在如圖3所示的圓臺中,AC是下底面圓O的直徑,EF是上底面圓O′的直徑,FB是圓臺的一條母線.

解析可以將圖3顛倒成圖4.
(1)證明:設FC的中點為I,連接GI,HI,在△CEF中,因為G是CE的中點,所以GI∥EF.又EF∥OB,所以GI∥OB.在△CFB中,因為H是FB的中點,所以HI∥BC.又HI∩GI=I,OB∩BC=B,所以平面GHI∥平面ABC.因為GH?平面GHI,所以GH∥平面ABC.

圖3 圖4



上述兩大策略是對文[1]的策略的應用舉隅,除此之外,還有如下策略:
三、分割法
分割法是一種求體積的方法,往往是把一個不規則的幾何體通過分割,劃分成錐體與柱體的組合體.實際上命題者想通過分割,對學生掌握體積公式知識的考查,以及對化歸能力的一種提升.

圖5
例3 (景德鎮市2017屆高三上學期期末考試)斧頭的形狀叫楔形,在《算數書》中又稱之為“鄆都”或“壍堵”:其上底是一矩形,下底是一線段.有一斧頭:上厚為三,下厚為六,高為五及袤為二,問此斧頭的體積為幾何?意思就是說有一斧頭形的幾何體,上底為矩形,下底為一線段,上底的長為3,下底線段長為6,上下底間的距離(高)為5,上底矩形的寬為2,則此幾何體的體積是( )
A.6 B.10 C.16 D.20
解析如圖6所示,過點A作AM⊥EF,垂足為M,連接MD.
過點B作BN⊥EF,垂足為N,連接NC.
則三棱柱ADM-BCN為直三棱柱,三棱錐E-ADM與三棱錐F-BCN全等.
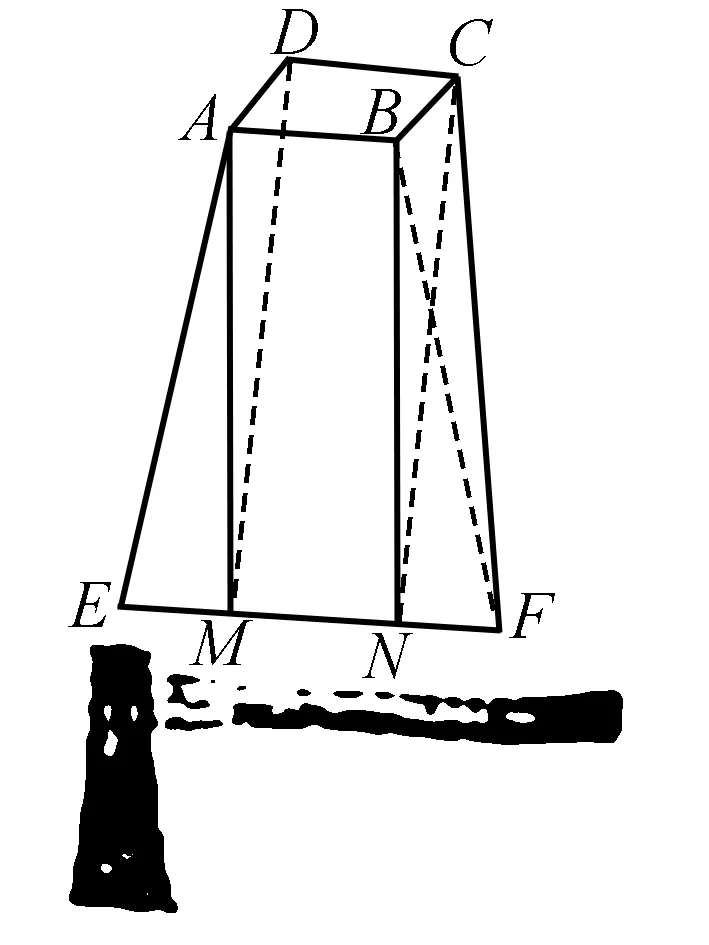
圖6
點評像例3中,不僅對中國古代數學文化考察,又考察了分割法,要在短時間內準確地對圖形做出分割,實屬不易.“分割路不易,且行且謹慎”.
四、模型法
模型法一直是三視圖中的一種重要的方法,可以彌補部分同學的空間想象能力的不足,利用模型可以解決線段,角度,體積等問題.



圖7

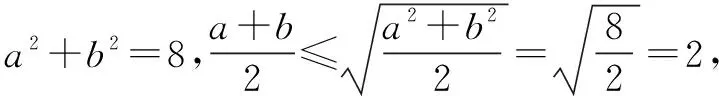
點評像例4,不用長方體模型的話,幾乎很難做出來,有人形容三視圖問題是“橫看成嶺側成峰”,但我們只要站在長方體的“肩膀”上,就會“一覽眾山小”.
總結遇到立體幾何問題時,原則上可以用上面的策略解決.五種策略的運用能很好地鍛煉學生的思維.立體幾何題目千變萬化,但只要掌握其本質,就能一招制敵.同樣學生在做題時,必須具有一題多解,多題一解的能力,這樣才能在做題時,多角度,多思維的去考慮,才能在做題中達到自身水平的提高.
參考文獻:
[1]朱小扣.解決立體幾何的三種方法[J].數理化解題研究,2016(28).

