圓錐曲線的解題方法探析
徐 博
(吉林省德惠市實驗高中二年七班 130300)
由于圓錐曲線解題過程比較復雜,許多同學對此感到解題困難,這主要是由于沒有掌握圓錐曲線的解題方法策略與技巧.圓錐曲線的解題方法技巧不少,需要掌握多種方法策略,這樣才能在解題時靈活運用,從而提高解題效率.
一、運用化歸方法解題,能夠降低解題難度
在遇到復雜的圓錐曲線問題時,可以運用化歸的思想方法,把所求的問題轉化成簡單的問題,這樣就能有效降低解題難度.雖然圓錐曲線具有復雜性和綜合性特點,但是圓錐曲線解題本質是用代數方法來解決幾何問題,實際上是把幾何問題與代數問題進行了相互轉化.運用化歸的數學思想方法,就能容易解決復雜的圓錐曲線問題.
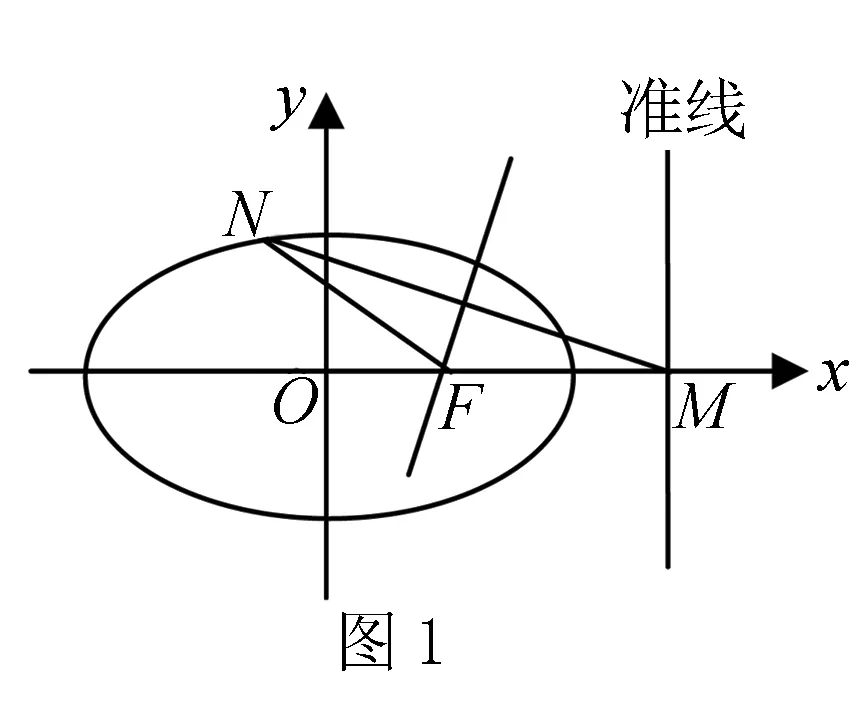
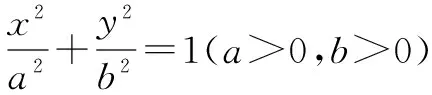
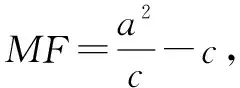
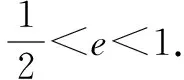
點評在求解此題時許多同學對此沒有思路,是因為對題目中的條件:“在橢圓上存在一個點N,能使MN線段的垂直平分線經過點F.”不能進行有效的轉化,造成解題困難.如果能把上述條件轉化成:“在橢圓上存在一點N,使得MF=NF.”這樣就能使題目容易解決.
二、運用分類討論方法,能夠全面綜合解題
在解題時遇到多種情況,需要對題目進行分類討論,對每一種情況進行逐個求解,然而進行綜合歸納,就能提高解題的全面性和綜合性,使解題的過程既不遺漏也不重復.
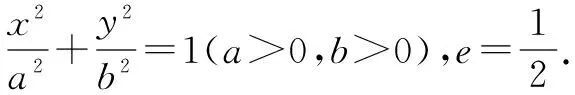
(1)求出橢圓的方程.
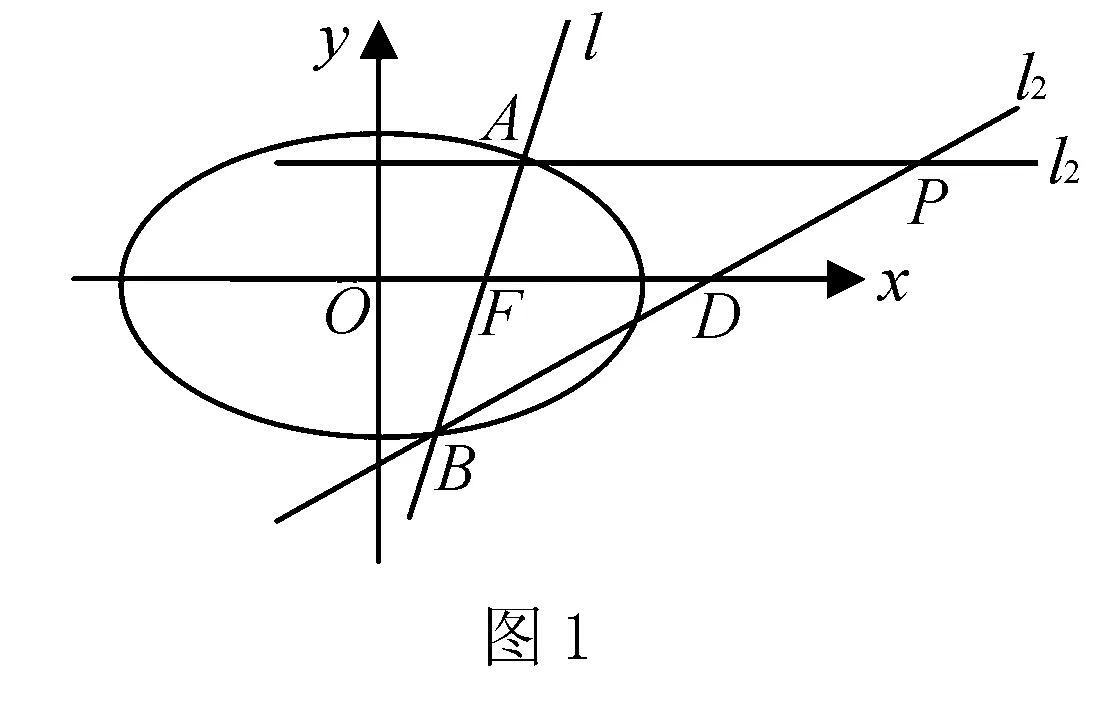
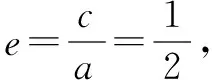
(2)本問可用多種方法求解.
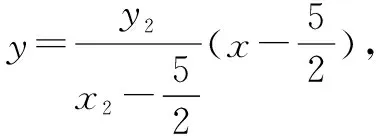
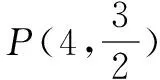
點評本題雖然假設了A、B兩點的坐標,但是并不求解,而是運用韋達定理進行求解,這樣能簡化計算過程.由于題目中所給的直線方程l中含有參數m,直線方程不確定,一般情況下需要分情況進行討論,而直線l與x軸垂直是一種特殊情況,假如垂直時l2直線存在,它肯定符合上述情況,可通過特殊情況找出該直線,然后再驗證該直線是否符合題意.
三、運用向量方法解題,創新解題方法技巧
運用向量的方法解決圓錐曲線問題非常方便快捷,解題時應遵循三個步驟:先將圓錐曲線問題轉化成向量問題,利用向量進行計算,最后再把向量計算的結果轉化成圓錐曲線問題.其中的把圓錐曲線問題轉化成向量問題是該方法應用的關鍵.
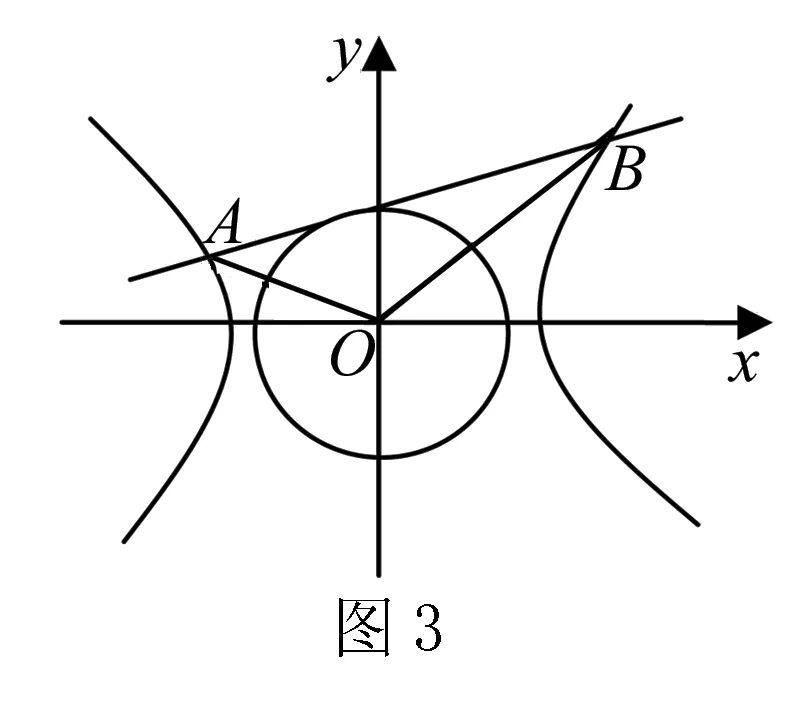
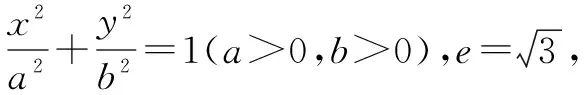
(1)求雙曲線方程.
(2)已知圓O方程是:x2+y2=2,在其上有一個動點P(x0,y0),(x0y0≠0),過P點的切線l與雙曲線相交于A、B兩點,求證:∠AOB的大小為定值.
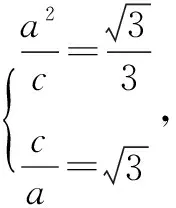
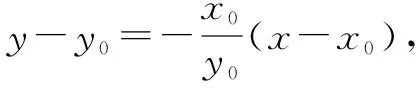
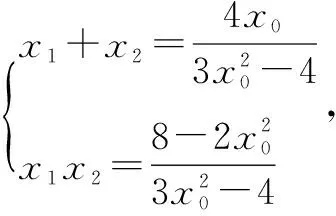
∴可證明兩向量垂直,即∠AOB=90°.
點評運用向量的加法、減法及其幾何意義、平面向量的數量積及其幾何意義來解決圓錐曲線問題非常方便快捷,因此,應注重發揮向量在圓錐曲線解題中的應用,從而提高解題效率.
總之,要提高圓錐曲線的解題效率,就要掌握解題的多種方法和技巧并加以靈活運用,才能高效解題,由于圓錐曲線解題的方法較多,本文只選取了三種,希望能起到拋磚引玉的作用.
參考文獻:
[1] 賴春葵.高中數學圓錐曲線教學及在解題中的應用探析[J].數學學習與研究, 2015(3).
[2] 戴錦權.從考題探析圓錐曲線題解題策略[J].理科考試研究,2013(13).

