基于多元概化理論的中小學教師資格考試數學學科試卷質量分析

趙 軒

?

基于多元概化理論的中小學教師資格考試數學學科試卷質量分析

趙 軒

（教育部考試中心，北京 100084）

中小學教師資格考試《數學學科知識與教學能力》科目，考查新入職中學數學教師所必需的學科知識與教育教學能力．應用多元概化理論對中小學教師資格考試中學數學學科試卷進行質量分析，以期為優化試卷結構、修訂考試大綱提供參考依據，進而促進中學數學教師資格考試質量的提升．

中小學教師資格考試；多元概化理論；測量信度

概化理論（GT，Generalizability Theory）是在經典測量理論（CTT，Classical Test Theory）的基礎之上，通過方差分析的技術研究測驗信度的測驗理論，可針對不同情境估計測量誤差的多種來源．多元概化理論（MGT，Multivariate Generalizability Theory）在概化理論的基礎之上，進一步研究測量目標在某個特定的全域之上具有多個全域分數的相關問題．這一理論被廣泛應用于考試、表現性評價等諸多方面，對教師的教學評價等也有直接的幫助[1]．

中小學教師資格考試是檢測申請人是否具備從事教師職業所必需的教育與教學能力的水平考試[2]．《中小學教師資格考試大綱（試行）》規定中學數學學科的考查內容包括學科知識、課程知識、教學知識和教學技能[3]．應用多元概化理論模型對該科目試卷的測試結果進行分析，可定量比較各考查內容模塊的區分度與內部一致性，并為試卷結構、各模塊分數比例分配、信度等方面的研究提供理論框架．

應用多元概化理論對中小學教師資格考試中學數學學科試卷進行分析，以期為改進試卷結構、修訂考試大綱，進而提高命題質量提供參考依據．

1 研究工具與研究樣本

1.1 概化理論簡介

概化理論是一種能夠達到區分考生、評估應考者真實水平的目的，并較好地控制測評誤差的現代測量理論．該理論采取數學建模和統計調整的方法，重點討論考生能力水平與考試題目之間的實質性關系；其基本原理是運用實驗設計的思想，分析與測驗分數差異相關的各項因素（如考生個體水平差異、題目難度差異等），并運用方差分析的技術，以方差分量作為指標分別估計各項因素對分數總變異的影響．概化理論的一個主要功能是可以在各種限定條件下估計測驗信度，并給出各因素與信度的相關性．在該理論中，測量信度的概念用概化系數或可靠性系數來代替[1]．

概化理論用方差分析的方法估計各種方差成分的相對大小，并可對其大小進行直接比較；不僅能估計出主效應，也能對交互效應進行估計和直接比較．在概化理論中，通過理論計算估計各方差成分相對大小的過程，稱為概化理論的G研究．

概化理論還要通過實驗性研究，進一步考察不同測驗設計條件下概化系數的變化狀況，如試題容量變化對于概化系數的影響．從而尋找最佳的誤差控制方法，作出最佳的設計決策，為改進測驗的內容、方式方法等提供有價值的信息．這一階段稱為概化理論的D研究[4]．D研究的研究對象和樣本可設定為G研究的子集．G研究確定測量對象、測量模式并對各項因素的變異數進行總體估計，D研究建立在G研究的基礎上，根據研究目的的需要，對測量對象樣本容量、測量模式等進行調整，進而在調整后的特定條件下估計各種測量誤差與指標，為改進測量提供信息參考．

多元概化理論在概化理論的基礎上，深入研究測量目標具有多個全域分數等方面的問題（如總測驗可以分解為多個不同維度的分測驗）．主要可應用于測試多門學科或多種能力的綜合測驗[1]．近年來，這一理論被廣泛應用于高考、研究生考試等大規模教育考試中，拓展了傳統測試的信度檢驗方式[5-6]．

1.2 研究樣本說明

從參加2017年上半年中小學教師資格考試《數學學科知識與教學能力（高級中學）》科目的全部19?359名考生中隨機抽取1?000名考生作為樣本，有效試卷為1?000份．該科目為考查考生多種能力的綜合性測試，因此對其測驗信度進行研究適宜采用多元概化理論的原理和方法．多元概化理論模型相關參數的計算采用mGENOVA程序（Brennan，2001）[7]．

2 研究方法

2.1 G研究設計

按照考試大綱的試卷結構，將全部試題劃分為“學科知識”、“課程知識”、“教學知識”和“教學技能”4個分測驗（下文中分別以V1、V2、V3、V4表示，其中V1為學科知識，V2為課程知識，V3為教學知識，V4為教學技能）．全卷共17道題目，滿分150分．V1包含10道題目，共61分；V2包含3道題目，共27分；V3包含2道題目，共12分；V4包含2道題目，共50分．

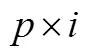
2.2 D研究設計

為了探討各個分測驗對于估計測驗總分可靠性的貢獻程度，考察了各模塊樣本容量變化對于各自測量信度及總分測量信度的影響情況，為優化試卷內容和結構提供了建議和參考．

3 研究結果與分析

3.1 4因子概化模型的G研究

根據G研究設計，使用mGENOVA軟件計算得到考生（）、試題（）以及考生和試題之間的交互效應（）在4因子上的方差與協方差分量的估計矩陣．如表1所示．

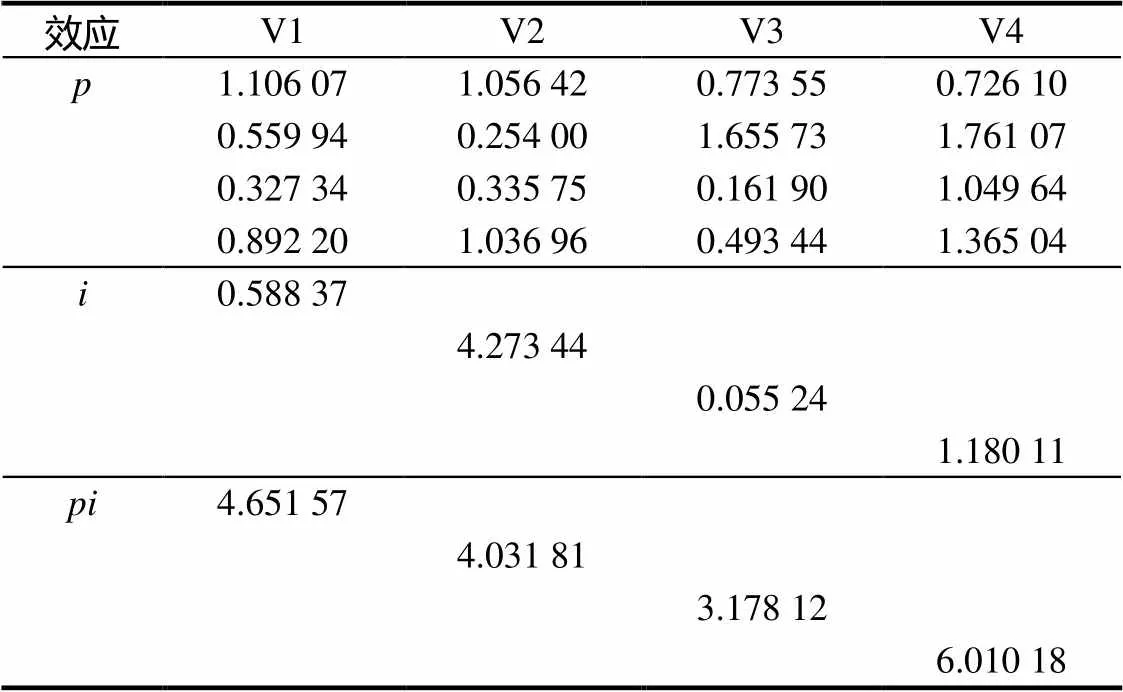
表1 G研究中各效應在4因子上的方差與協方差分量估計

注：主對角線上的元素為各效應在相應因子上的方差分量估計，主對角線以下元素為各效應在不同因子間協方差分量的估計，主對角線以上元素為因子間相關系數的估計．

從中可見，4因子中考生效應（）方差分量最小的因子為教學知識模塊（0.161?90），其次是課程知識模塊（0.254?00）；方差分量最大的是教學技能模塊（1.365?04），其次是學科知識模塊（1.106?07）．這說明在此次考試中，教學知識和課程知識模塊的區分作用較小，教學技能和學科知識模塊的區分作用較大；其中一個原因是教學知識和課程知識模塊總分值較低，教學技能和學科知識模塊總分值較高．此外教學技能模塊所含各小題分值較高，因此其總分值雖低于學科知識模塊，但方差分量卻大于學科知識模塊．

此外，根據協方差分量的估計值，4因子之間的協方差分量均大于0.3，這說明不同考生在各模塊中的得分順序較一致，即整卷內部一致性與各模塊題目的區分度均良好．

考生效應（）反映了考生水平差異造成的成績變異大小，試題效應（）反映試題難度差異造成的成績變異大小，而交互效應（）反映考生和試題因素交互影響產生的誤差，不同效應之間方差分量值不可直接比較．從表1試題效應（）部分中還可看出課程知識模塊由試題難度差異造成的成績變異最大，說明該模塊所含試題難度跨度相對較大．

3.2 4因子概化模型的D研究

（1）各因子全域分數估計的測量精度研究．

使用mGENOVA軟件可計算考生在4個因子上全域分數與相應誤差估計的方差分量，以及概化系數、可靠性系數和信噪比，結果如表2所示．

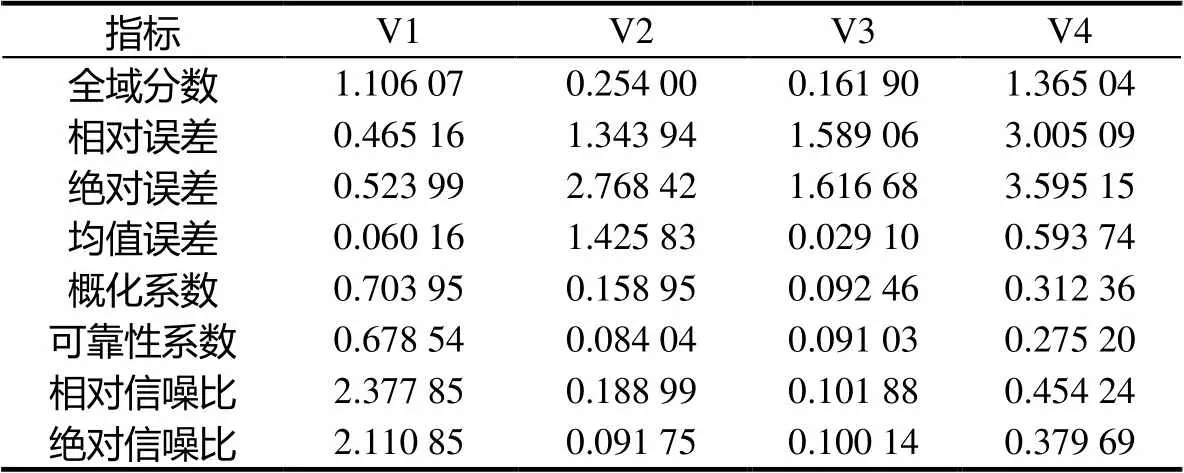
表2 全域分與相應誤差在4因子上的方差分量等指標估計

從表2中可見，考慮到誤差因素，概化系數（信度）最高的是學科知識部分（0.703?95），其次是教學技能部分（0.312?36），課程知識（0.158?95）和教學知識（0.092?46）部分較低．這說明此次考試對學科知識模塊的測量精度較高，教學技能模塊的測量精度可以接受；而課程知識和教學知識模塊的測量誤差較大，一個可能的原因是在這兩個模塊中，考生各題目得分之間的內部一致性較低．

（2）全域總分的測量精度研究．

按照各模塊題量所占比重來決定權系數（見表3），對4因子全域分數進行合成，可得到全域總分與其相應誤差估計的方差分量，以及全域總分的概化系數、可靠性系數和信噪比，結果見表4．

表3 D研究中4因子合成全域總分的權系數

表4 D研究合成全域總分與相應誤差方差分量等指標估計

從表4中可見，全域總分的概化系數為中等水平（0.742?33）；相對誤差不大（0.266?39），因此相對信噪比較高（2.880?97）．這說明此次考試的總體測量信度是可以接受的．

（3）各因子對總方差貢獻度的研究．

用各模塊全域分數與相應誤差估計的方差分量，可計算出各模塊對總方差的貢獻度，見表5．

由表5可見，各模塊對全域分數方差的貢獻比例與考試大綱規定的賦分比例存在一定差距，特別是在學科知識和教學技能兩個模塊表現得較為突出．學科知識部分賦分比例為40.67%，方差貢獻率為68.44%；教學技能部分賦分比例為33.33%，方差貢獻率為14.20%．其可能原因在于學科知識部分題目容量大，且一半是客觀題（6題，30分），成績分布分散；而教學技能部分只包含兩個題目，分值較大，且均為主觀題，成績分布較集中．這說明整套試卷中，學科知識部分的題目在區分考生能力上的功能最好，即試題區分度最高．因此增加這部分試題的比重，或在其它部分試題中加強對學科知識的考察，都能夠提高試卷對于考生的區分能力，進而提高考試信度與區分效果．

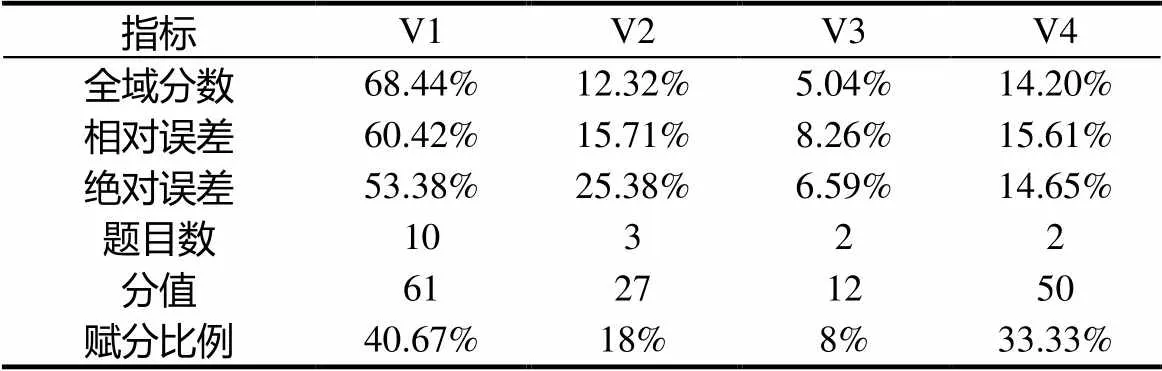
表5 各模塊方差分量對總方差貢獻度與試卷賦分比例比較

（4）各因子題目容量對測量精度的影響研究．

為研究進一步提高考試測量精度的方法，研究者改變各因子所含題目數量，并觀察測驗信度隨之產生的變化，具體結果見表6．

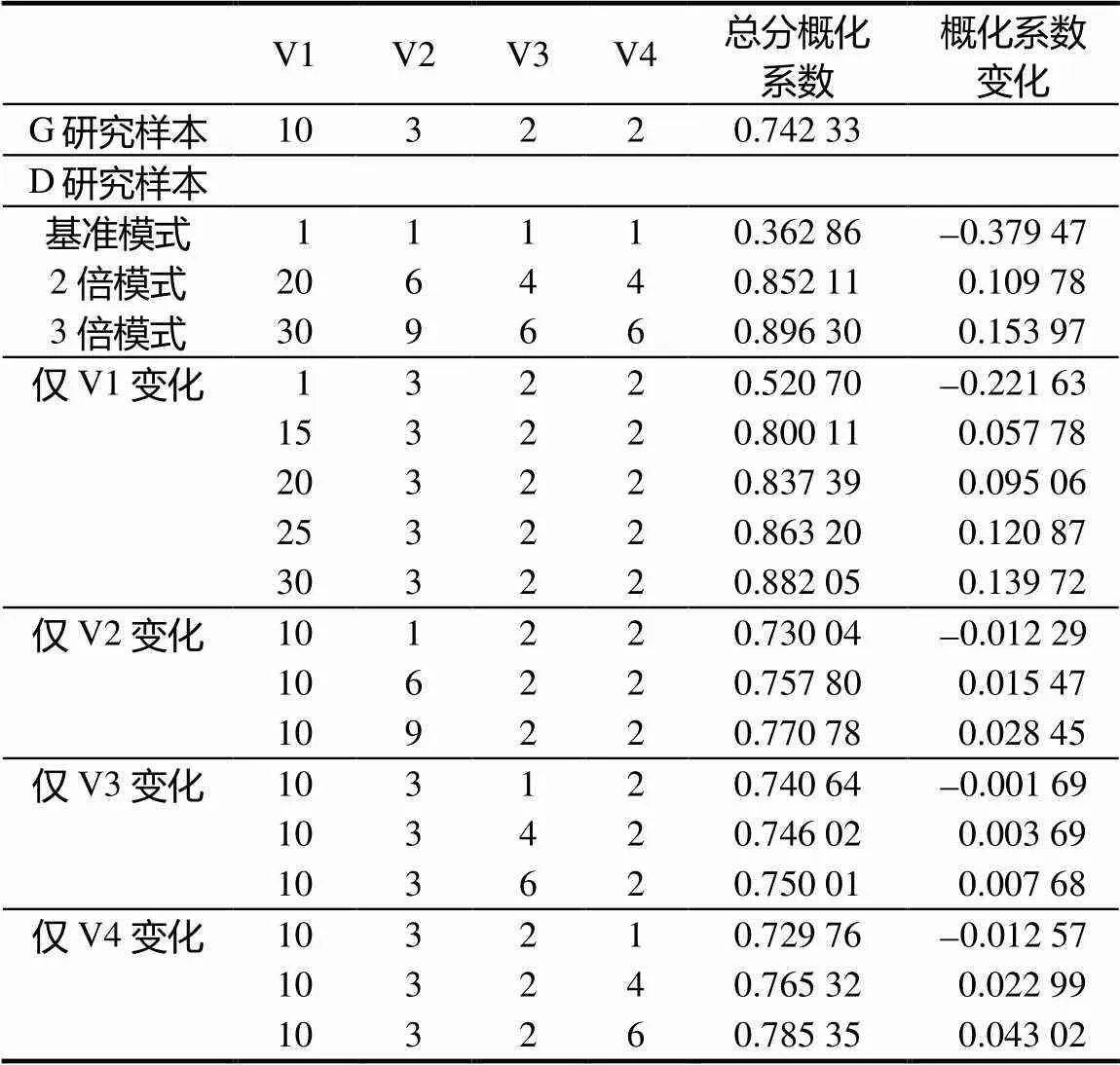
表6 D研究中各因子題目容量對總分概化系數的影響

從中可見，各因子樣本容量增加為2倍和3倍時，測量信度將大幅提升，這說明增加考試題量可以提高考試信度，這一結論和CTT的結論是一致的．分別固定4個因子中3個因子的樣本容量，變化其中一個因子的樣本容量時發現，單獨增加每個因子的樣本容量，都會提高測量信度，但提升的幅度不同．4因子對應的提升幅度從大到小分別為：學科知識、教學技能、課程知識和教學知識，這與前文的分析是一致的．

由于受到考試時間的限制，大幅度增加題量是不現實的，不具可操作性．但仍可通過其他技術手段達到同樣效果，如適當增加題量，小題增加中間分，大題拆分題目分數、增加得分點等方式．可以此來增加整卷的分數檔，從而提高試卷的信度與區分效果．

4 研究結論與思考

應用多元概化理論對中小學教師資格考試《數學學科知識與教學能力》科目試卷進行分析，得到如下結論：

（1）試卷全域概化系數為0.742?33，屬于中等水平，相對誤差不大，各部分試題區分度良好，試題試卷整體質量較高．

（2）各部分試題的方差貢獻度與考試大綱賦分比例基本相符，說明現有試卷結構較合理，考試基本達到了大綱設計的考查目的．

（3）學科知識、課程知識、教學知識和教學技能4個模塊中，學科知識模塊對于總方差的貢獻度最高，且增加學科知識模塊的題目容量對于測量信度的提升最大．因此，在考試時間和總題量不變的前提下，可通過適當增加學科知識部分考核比重的方式來實現進一步提高考試測量信度的目的．

（4）各模塊題量均與測驗信度正相關，因此可采取適當增加題量，小題增加中間分，大題拆分題目分數、增加得分點等技術手段提高試卷的信度與區分效果．

多元概化理論的引入，為探索教師資格考試的質量評價方式提供了更多的可能性．從研究結果來看，一方面，對于試卷結構的調整，雖受限于考試時間、考試大綱對試題分數分布等確定性要求，但多元概化理論對試卷的質量分析結果提供了在現有結構下的精細化調整方案．另一方面，運用多元概化理論進行試卷結構分析，在統一題型和各模塊分值的前提情況下，其結論更有針對性．因此，多元概化理論對于研究中小學教師資格考試的質量評價有重要的意義，與經典測量理論的評價結果相結合，可以得到更為準確的試題單題質量和試卷整體質量改進方案．

總之，通過引入多元概化理論對教師資格考試的試卷質量進行分析和評測，可以為今后完善考核內容，調整試卷結構，修訂考試大綱提供參考，為改進試題試卷質量提供依據．進一步加強概化理論等基于真實數據的實證性研究，對于提升考試的科學化水平，支撐考試的可持續化發展具有重要意義．

[1] 楊志明，張雷．測評的概化理論及其應用[M]．北京：教育科學出版社，2003．

[2] 余仁勝，趙軒．中小學教師資格考試測試結果的統計分析研究[J]．中國考試，2015（1）：32-39．

[3] 中華人民共和國教育部．中小學教師資格考試筆試大綱（試行）[EB/OL]．（2017-05-18）[2017-06-20]．http://ntce. neea.edu.cn/html1/report/1508/369-1.htm.

[4] 劉遠我，張厚粲．概化理論在作文評分中的應用研究[J]．心理學報，1998，30（2）：211-218．

[5] 關丹丹，任子朝．應用概化理論評價課標后高考數學試卷[J]．數學通報，2009，48（11）：18-24．

[6] 白娟．基于多元概化理論的全國碩士研究生中醫綜合考試質量分析[J]．天津中醫藥大學學報，2014（2）：44-46．

[7] BRENNAN R L. Generalizability theory [M]. New York: Springer-Verlag, 2001: 55.

[8] 趙軒．注重能力考查，推動專業化建設——中學數學教師資格考試目標要求和試題特點及測評情況分析[J]．數學教育學報，2016，25（6）：7-9．

Quality Analysis in Math Subject of National Teacher Certification Examination Based on Multivariate Generalizability Theory

ZHAO Xuan

(National Education Examinations Authority, Beijing 100084, China)

“Subject knowledge and teaching ability of Math”, which was one subject of National Teacher Certification Examination, mainly focused on the basic quality of subject knowledge, and education and teaching ability of new middle school Math teachers. This manuscript applied the Multivariate Generalizability Theory to Math subject of National Teacher Certification Examination for quality analysis, aimed to provide the reference quantified data to improve the structure of examination and modify the examination syllabus, and then promote the quality of middle school Math Teacher Certification Examination.

national teacher certification examination; multivariate generalizability theory; test reliability

[責任編校：周學智]

2017–10–28

趙軒（1983—），男，北京人，助理研究員，主要從事考試研究與數學教育測量研究．

G424.74

A

1004–9894（2018）02–0038–03

趙軒．基于多元概化理論的中小學教師資格考試數學學科試卷質量分析[J]．數學教育學報，2018，27（2）：38-40．