公交停靠站區域長度優化研究

宮克，羅鈿

（1.長安大學汽車學院，陜西 西安 710064；2.蘭州工業學院汽車工程學院，甘肅 蘭州 730050）

引言

公交停靠站的區域長度是衡量公交停靠站通行能力的重要指標。公交停靠站的區域長度對停靠站的通行能力和泊位的有效利用率都具有重要的影響。

對于公交停靠站區域長度的取值，若公交停靠站的區域長度過短，則到達停靠站的公交車輛必須在站外等候排隊進站。尤其在距離信號交叉口較近的停靠站，還會降低交叉口通行能力及公交停靠站的通行能力。在這種情況下，不僅會造成乘客等待公交出行的時間成本增加，還會降低社會車輛和與之受影響的其他交通工具的運行效率；反之，若公交停靠站區域設計長度過長，雖然從理論上提高了公交停靠站的通行能力，但造成公交車輛無序進站停靠，停靠站的實際通行能力并不隨停靠區域長度的增加而增加，公交停靠站的有效使用效率降低，浪費用地，增加停靠站成本，無形中造成不必要的浪費。

1 公交停靠站區域長度分析基本思路

確定公交停靠站區域長度時，通常有以下兩種思路：

第一種思路：公交停靠站區域長度直接影響公交停靠站通行能力，對于需要新建的停靠站，可以先計算或預測出站點的通行能力，根據通行能力，確定滿足需求的公交停靠站泊位數，以確定停靠站的區域長度[1]；對于需要改建的站點，先計算現有公交停靠站泊位數所能提供的通行能力，將其與此站點實際公交流量比較，從而可知現有站點公交停靠的區域長度能否滿足需求。

第二種思路：公交車到站規律近似服從何種分布，服務時間的規律，研究公交車輛在某時間段內的排隊長度和滿足停靠需求的緩沖空間。這兩個參數作為確定停靠站的區域長度的重要依據。

2 基于車輛到達的停靠站區域長度模型

2.1 平均排隊長度

步驟1：每輛車到達時的排隊車輛數確定

根據馬爾可夫理論，定義泊位上的公交車輛離開的瞬時時刻作為一個再生點，兩個連續再生點間的時間間隔為一個周期[2]。

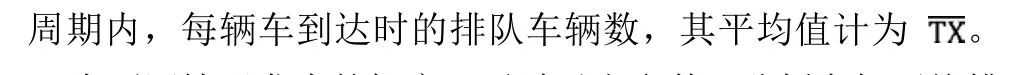
對以下五種情況進行分析：

情形1：第n個周期之初和之末，停靠站區域內無排隊車輛。在該種情況下，第 n個周期內無車輛排隊，即i=j=0,TX=0。

情形2：第n個周期之初，有i輛車排隊等候，且排隊車輛不超過泊位數。但在該周期末，系統內車輛全部清空，即 i≤c，TX=0。

情形3：在第n個周期之初無排隊車輛，但在該周期末，進入系統的車輛未清空，有 j輛車排隊等候出站，即i=0,j>0,TX=j。

情形4：第n個周期之初，i輛車排隊等候，等待車輛數不超過泊位數；該周期末排隊車輛未清空，仍有j輛車排隊。在該種情況下，整個周期內，停靠站滿負荷；當c-i車輛到達時，所有未滿泊位占滿，第c-i+1輛車等待服務。j-1輛車依次排隊形成從1到j-1的長隊列，即：

情形5：第n個周期之初，i輛車排隊等候，且排隊車輛數大于泊位數；該周期末，仍有j輛車排隊且j≥i-c＞0。在這種情況下，第 i-c輛車仍然滯留在隊列進口處，后續到達車輛依次形成i-c，i-c+1，…，j-1的序列，即：

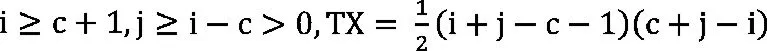
步驟2：轉移概率Pij的確定

理想狀態下，不考慮城市道路的交通情況、信號交叉路口等因素的影響，按照發車時刻表，公交車輛會以確定的時間間隔均勻到達每個公交停靠站。高峰時段，到達時刻處于不可接受間隙期間。該情況下，到達車輛必須等待可接受間隙之間的車輛通過后，可接受間隙出現時方可通過。此時，車輛間相互影響比較微弱時，因而路段交通流可以近似采用泊松分布加以描述[3][4]。

根據假設條件，車輛的到達過程滿足泊松過程，在停靠站內的停留時間滿足定長分布，五種不同情形的概率為：

當泊位數C一定，則取決于五種情形的i、j、TXn。因此，通過加權平均的方法獲得：

步驟3：平均排隊長度的確定

c—泊位數(個)；

dv—公交車輛長度(m)；

ds—停靠站內公交車輛的安全距離 (m)，為了保證公交車輛在站內停靠的安全性，站內公交車輛之間的安全距離通常為3米[5]。

對于港灣式停靠站，要考慮加速漸變段與減速漸變段長度。由運動學知識，漸變加速段和漸變減速段的計算公式為

[6]：

漸變加速段長度為：

d—公交車輛進出站的減速度(m/s2)；

VT—公交車輛通過速度（m/s）；

VT—公交車輛站內速度（m/s）。

步驟5：參數的標定

（1）λT的確定

λ為高峰時段公交車輛的到達率，輛/秒；T為確定的單位時間，s。λT—T時間內，到達的平均車輛數。

將在目標停靠站采集到的實際數據進行換算，可通過以下公式計算：

Q為實際調查每小時車流量，pcu/h。

（2）最大到達車輛數Qn的確定

設車輛到達過程服從泊松過程，設Tn為第n個周期的時間，KTn為第n個周期內到達的車輛數。因此，

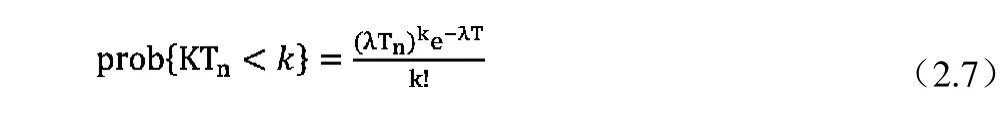
其中，λ-高峰時段車輛的到達率，輛/秒；λT—第n個周期內到達的平均車輛數。

假設置信概率為α，則在車輛在 Tn內的最大車輛數為Qn。由此可知：

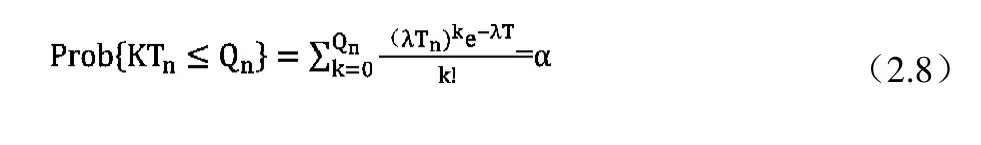
3 實例分析

車輛到達服從泊松到達過程，取置信概率為α=0.997，則在車輛時間T內的最大車輛數為Qn。由公式2.8知，在周期內最大到達車輛數Qn=5。通過公式2.1得：

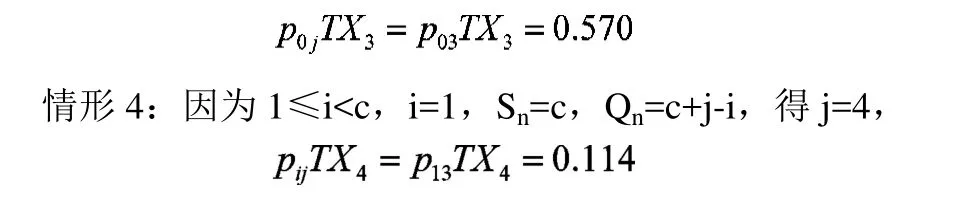
（3）情形 5：i≥c，即 i≥c 且 j≥i-c＞0。

i為周期之初排隊的車輛數，此時可通過第n-1個周期末滯留的車輛數得出。

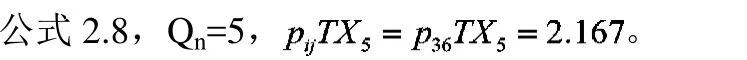
為了滿足公交停靠站線路容量和停靠要求，根據高峰時段確定的平均排隊車輛數，翠華路公交停靠站的區域長度至少要滿足三輛車同時在站時的長度。

對于直線式公交停靠站的區域長度為車輛平均排隊長度與停靠站內公交車輛間的安全距離相加。為了研究的統一性和合理性，以便在VISSIM仿真過程中參數的標定和統計結果的分析。因此，取VISSIM仿真軟件公交車輛的長度默認值11.54m，停靠站內公交車輛之間的安全距離通常取為3米。因此，VISSIM 仿真軟件，該公交停靠站的區域長度應該設置為43.62m。

4 VISSIM仿真分析

4.1 基本參數的確定

4.1.1 基本交通狀況

陜西省西安市雁塔區小寨東路連接小寨商圈與大雁塔旅游區，小寨東路的翠華路站位于翠華路與小寨東路交叉口上游55m處，北臨陜西省歷史博物館。小寨東路與翠華路交叉口所在道路情況：北進口道路為雙向四車道，單車道寬度為3.5m；東、西、南進口道路均為雙向六車道，單車道寬度為3.5m。

小寨東路翠華路公交停靠站距離下行方向的人行橫道35.6m。在調查區域內和時間內，無社會車輛停靠和非機動車停靠。路面平整、坡度符合設計要求[10]。停靠站形式為直線式，區域長度24m，設計泊位2個。

4.1.2 公交車高峰時段的發車間隔及清空時間

通過對小寨東路翠華路公交站的實際調查情況可知，高峰時段車輛的到達密度較大。因此，考慮到數據的準確性，調查該停靠站所在的上游交叉口的信號周期為120s。因此，在車輛時間間隔的調查過程中，以120s作為一個時間單位，記錄相繼到達停靠站公交車輛的時間。記錄早高峰（7：30-8：30）和晚高峰（18:0 0-19:00）這兩個高峰時段的同線路公交車的到達時間，然后計算相繼到達的同線路公交到達時間的間隔，求多組數據的平均值。通過對翠華路停靠站的實際調查，12條公交線路的公交車輛在高峰時段公交車輛的平均到達間隔為△T=17s。

清空時間由公交車輛啟動和行駛出停靠泊位的時間和公交車輛重新匯入車道的等候時間之和確定。通過實際的觀測值，該值在9s-20s之間[2]。對于直線式停靠站，不計入公交車輛重新匯入車流的等待時間。因此，在翠華路站的仿真參數的設定中，清空時間TC=15s。

通過實際情況的調查，翠華路站現有區域長度設置為24m。在線路容量、車流量、公交車發車間隔、公交車站內清空時間等參數不變的情況下，將直線式停靠站改建為港灣式停靠站。VISSIM軟件中默認車輛速度分布為30-35km/h，市內公交停靠站內的速度為 13-23km/h[10]。因此，確定停靠站停靠區域長度為36m。

4.2 仿真結果分析

4.2.1 排隊長度對比分析

模型結果的仿真結果：隨著仿真時間的增加，數據穩定性會更好；對于上游排隊檢測器，1800-4800s仿真時間內，平均排隊長度為僅為 2m。公交車輛對于整個停靠站系統的負荷較小；對于下游排隊檢測器，1800-4800s仿真時間內，平均排隊長度為27m。通過馬爾可夫模型的計算結果，該停靠站的設計泊位數為3個。

針對實際情況，通過VISSIM仿真，可得到以下結論：實際情況的仿真結果，上游排隊檢測器，2400-4200s仿真時間內，平均排隊長度為66m，最大排隊長度為97m。因此，車輛在停靠站區域進口處會出現排隊現象；對于下游排隊檢測器，3000-4800s仿真時間內，平均排隊長度為48m，最大排隊長度53m。實際情況下，該停靠站的設計泊位數為2個。因此，該停靠站的設計通行能力不能滿足高峰時段的車流量需求。

針對改建方案的仿真結果：對于上游排隊檢測器，1200-4800s仿真時間內，最大排隊長度為 98m。因此，車輛在區域進口處會出現排隊現象；對于下游排隊檢測器，3000-4800s仿真時間內，平均排隊長度為44m，最大排隊長度55m。改建方案，該停靠站的設計泊位數為2個。因此，該停靠站的設計通行能力不能滿足高峰時段的車流量需求。

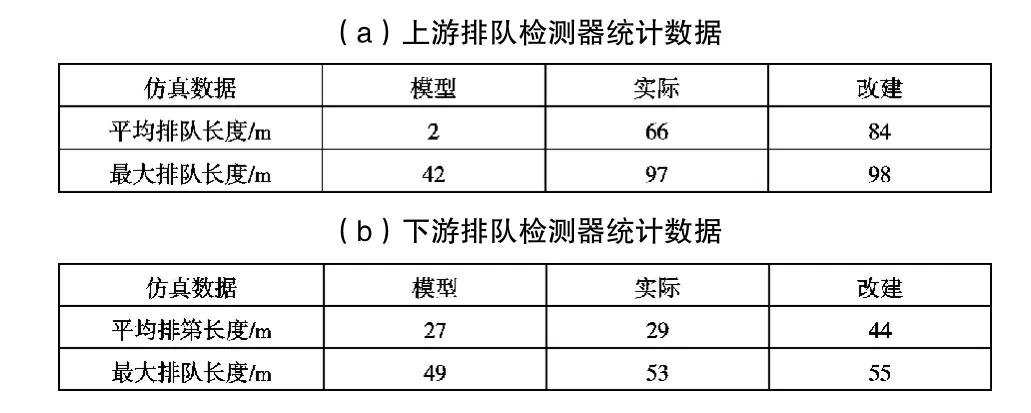
表 1 3600s仿真時間長度對比分析

3600s的仿真數據較為平穩。因此，取3600s仿真時間，分析三個仿真結果由圖1所示。

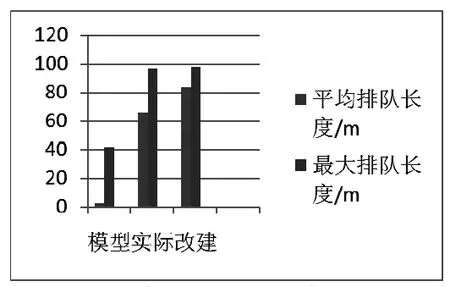
圖1 3600s仿真時間內上游檢測器排隊長度對比

如圖1上游排隊檢測器的檢測數據中，平均排隊長度和最大排隊長度反映了該公交停靠站區域進口處車輛的排隊情況和通行能力。基于馬爾可夫區域長度的模型優勢最為明顯。相比于其他兩個方案，平均排隊長度和最大排隊長度最小。

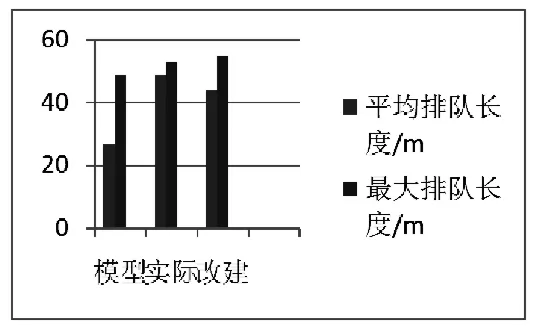
圖2 3600s仿真時間內下游檢測器排隊長度對比圖

如圖 2，下游排隊計數器采集到的數據中，平均排隊長度和最大排隊長度反映了停靠站區域內的車輛排隊情況和通行能力。基于馬爾可夫區域長度的模型優勢最為明顯。相比于其他兩個方案，平均排隊長度和最大排隊長度最小。

4.2.2 公交車延誤分析

隨仿真時間的增加，公交車延誤、平均停車時間和停車次數的數據穩定性愈好。根據調查，公交車的清空時間通常為9-20s，模型仿真結果得出的公交車的平均停車時間小于清空時間。

根據延誤最小原則，隨仿真時間的變化，基于馬爾可夫的停靠站區域長度模型的公交車總延誤最小。若將目前的直線式停靠站改為港灣式停靠站，公交總延誤較大。因此，就縮短延誤時間而言，基于馬爾可夫的停靠站區域長度模型有較大的優越性，如圖3。

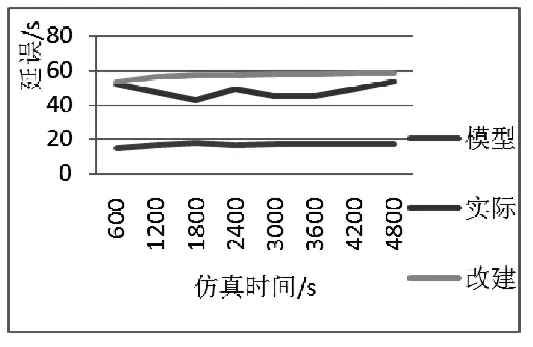
圖3 公交車輛延誤時間對比

同樣的，仿真時間3600s的數據穩定性較好，公交車延誤、平均停車時間、平均停車次數以及行程時間內的通過車輛數對比分析。

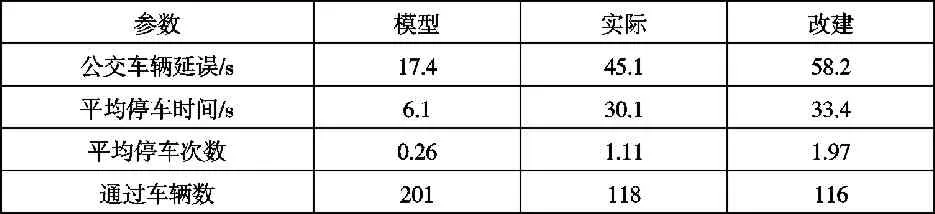
表2 3600s仿真時間內的延誤對比

從表2可知，在3600s仿真時間內，對應的停靠站區域長度，基于馬爾可夫的停靠站區域長度模型得出的仿真結果中，公交車延誤與平均停車時間最短，平均停車次數最少，相同時間內通過的車輛數最多。

4.3 優化方案的選擇

通過對馬爾可夫模型、實際情況和改建模型的仿真結果，馬爾可夫模型得出的結果相比于其他兩個方案，平均排隊長度和最大排隊長度較低小，延誤時間的值都較低。所以，基于馬爾可夫的停靠站區域長度模型的對于確定停靠站的區域長度有明顯的優越性。

將24m直線式停靠站改建為36m港灣式停靠站是不合理的，排隊長度增加，且延誤也隨之增加，用地面積增加，對路段通行能力造成較大的負荷。

對于翠華路停靠站，最優的選擇方案為將現有區域長度增加為43.62m，不需要改變現有的設施，只需劃定該區域范圍，通過道路標志標牌明確在高峰時段，該區域內，不允許社會車輛停靠；在平峰時段，則不做限制。因此，該種方案是具有較強的可行性，且最大程度上節約用地，改建成本較低。

5 結語

運用VISSIM仿真軟件，對典型的公交停靠站進行改造方案仿真分析，通過平均排隊長度、最大排隊長度以及公交車輛的延誤等統計結果，確定合理的改造方案，優化現有的停靠站區域長度。驗證馬爾可夫模型在確定停靠站區域長度的可行性及合理性。

參考文獻

[1] 何赟.多線路公交停靠站站址與站位問題研究[D] .成都:西南交通大學,2011

[2] Sheldon M .ROSS. Introduction to Probability Models[M]. 2010

[3] Akcelik R, Chung E.Calibration of the bunched exponential distribu-tion of arrival headways[J]. Transport Research,1994, （3）: 42-59.

[4] 肖和華,張顯尊等.公交停靠站設置形優化選擇研究[J]交通工程2011.9(18):45-50

[5] 建設部.中華人民共和國行業標準—城市道路設計規范CJJ37-90.北京:中國建筑工業出版社,1991

[6] 呂林.城市公交停靠站優化設計方法研究[D].南京:東南大學,2006.

[7] Fernández, R., 2007. Passion 5.0-a model for microscopic simulation of multiple-berth bus stops. Traf fi c Engineering and Control 48 (7),324-328.

[8] Basso, L. J. and H. E. Silva (2010). A microeconomic analysis of congestion management policies. 5th Kuhmo Nectar Conference in Transport Economics Valencia, Spain, July 8-9.

[9] Alejandro Tirachini. The economics and engineering of bus stops:Spacing, design and congestion[R]. The University of Sydney ,May 2012.

[10] 王煒,楊新苗,陳學武.城市公共交通系統規劃方法與管理技術.北京:科學出版社,2002.

[11] 李靜濤.基于 VISSIM 仿真的公交港灣式車站設置條件研究[D].石家莊:石家莊鐵道學院,2010.