中考題中的統計與概率

沈良琴

統計與概率知識在中考的選擇、填空、解答題中都會經常出現.結合條形統計圖、扇形統計圖和折線統計圖，利用平均數、眾數、中位數、方差等對數據進行分析，從而得出相應的結論；利用樹狀圖或列表的方法計算一些簡單事件發生的概率常以解答題形式出現.一般統計與概率在中考試題中占總分值的12%～15%.下面通過一些實例加以說明：

一、數據的收集、整理、分析

例1（2017·懷化）下列說法中，正確的是（ ）.

A.要了解某大洋的海水污染情況，宜采用全面調查方式；

B.如果有一組數據為5，3，6，4，2，那么它的中位數是6；

C.為了解懷化市6月15日到19日的氣溫變化情況，應制作折線統計圖；

D.“打開電視，正在播放懷化新聞節目”是必然事件.

【分析】本題考查了數據的收集與整理、數據的分析.解題關鍵是掌握全面調查和抽查的不同情況，掌握中位數的確定方法，知道什么情況下使用折線統計圖以及必然事件的概念.

【解答】選項A中某大洋中的海水面積非常廣闊，并且量特別大，因此不能采用全面調查，而應該抽樣調查；選項B中將這組數據從小到大排列為2，3，4，5，6，所以中位數是4；選項C中要反映溫度變化情況，最合適的統計圖是折線統計圖；選項D中隨機打開電視可能是懷化新聞節目，也可能是其他節目，所以“打開電視，正在播放懷化新聞節目”不是必然事件.故選C.

【點評】本題易錯點是在找中位數的時候，沒有把所有數據按照一定順序排列，就去找位于中間的數.

【變式練習1】（2017·烏魯木齊）下列說法中，正確的是（ ）.

A.“經過有交通信號燈的路口，遇到紅燈”是必然事件

B.已知某籃球運動員投籃投中的概率是0.6，則他投10次一定可投中6次

C.處于中間位置的數一定是中位數

D.方差越大數據的波動越大，方差越小數據的波動越小

【答案】D.

二、三數兩差

例2（2017·棗莊）下表記錄了甲、乙、丙、丁四名跳高運動員最近幾次選拔賽成績的平均數與方差：________________________

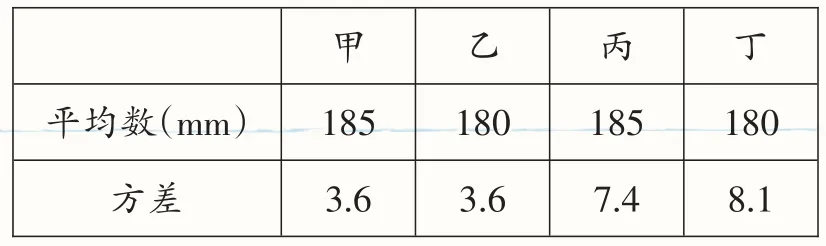
180 8.1_________________甲乙_____丙_____丁__平均數（mm）__方差_______185___3.6____180____3.6____185 7.4

根據表中數據，要從中選擇一名成績好且發揮穩定的運動員參加比賽，應該選擇（ ）.

A.甲 B.乙 C.丙 D.丁

【分析】首先比較平均數，平均數相同時選擇方差較小的運動員參加.

【解答】∵甲、丙的平均數大于乙、丁的平均數，又∵甲的方差小于丙的方差，∴甲的成績更穩定，應選擇甲參賽.故選A.

【點評】此題考查了平均數和方差，正確理解方差與平均數的意義是解題關鍵.

【變式練習2】（2017·青島）小明家1至6月份的用水量統計如圖所示，關于這組數據，下列說法中錯誤的是（ ）.

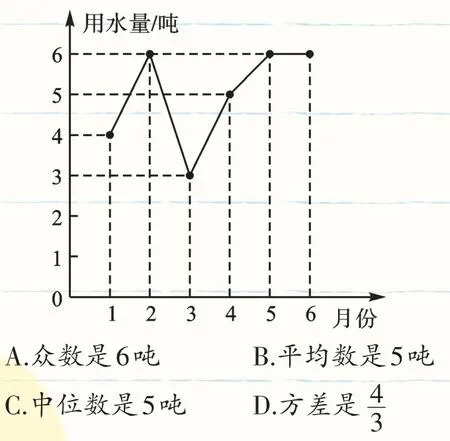
【答案】C.

三、統計圖表

例3（2017·大連）某校為了了解全校學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況，隨機選取該校部分學生進行調查，要求每名學生從中只選一類最喜愛的電視節目.以下是根據調查結果繪制的統計圖表的一部分.________________________________

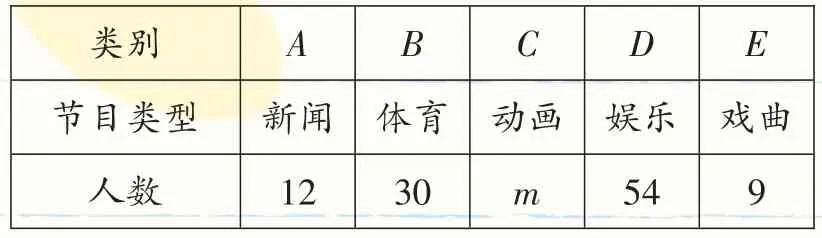
____類別__節目類型____人數A____B____C____D____E__新聞__12體育__30動畫_m娛樂__54____戲曲9__

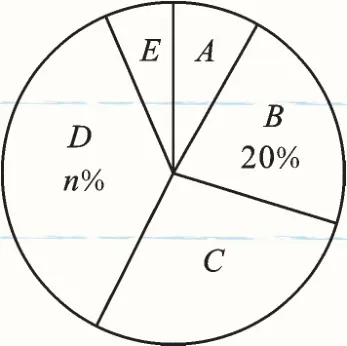
根據以上信息解答下列問題：

（1）被調查的學生中，最喜愛體育節目的有_______人，這些學生數占被調查總人數的百分比為_______%；

（2）被調查學生的總數為_______人，統計表中m的值為________，統計圖中n的值為_______；

（3）在統計圖中，E類所對應扇形圓心角的度數為_______°；

（4）該校共有2000名學生，根據調查結果，估計該校最喜愛新聞節目的學生數.

【分析】（1）直接通過表格讀取最喜愛體育節目的人數，通過扇形統計圖讀取喜愛體育的人數占被調查總人數的百分比；（2）通過喜愛體育的人數和占被調查總人數的百分比求出被調查學生的總數，用總數減去A、B、D、E項目的人數求出m值，用D項目的人數除以被調查學生的總數即可得到n的值；（3）求出E類學生數占被調查總人數的百分比，用這個百分比乘360°即可；（4）求出喜愛新聞節目的人數占被調查總人數的百分比，進而乘該校總人數求得結果.

【解答】（1）30，20；（2）150，45，36；（3）21.6；（4）解：，答：估計該校最喜愛新聞節目的學生數是160人.

【點評】本題考查了統計表和扇形統計圖，解題的關鍵是綜合運用統計表和統計圖給出的信息求出被抽查的總人數.

【變式練習3】（2017·泰州）“泰微課”是學生自主學習的平臺.某初級中學共有1200名學生，每人每周學習的數學泰微課都在6至30個之間（含6和30）.為進一步了解該校學生每周學習數學泰微課的情況，從三個年級隨機抽取了部分學生的相關學習數據，并整理、繪制成統計圖如下：

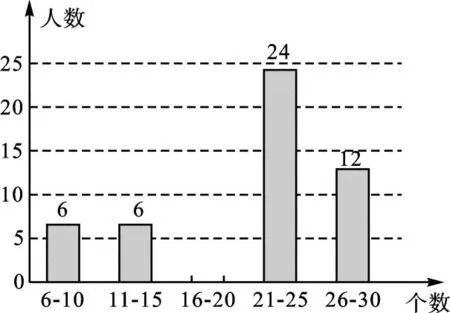
每周學習數學泰微課人數的條形統計圖

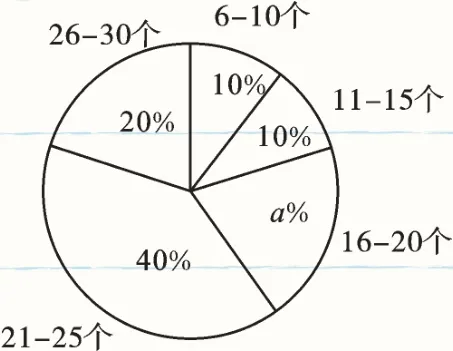
每周學習數學泰微課人數的扇形統計圖

根據以上信息完成下列問題：

（1）補全條形統計圖；

（2）估計該校全體學生中每周學習數學泰微課在16至30個之間（含16和30）的人數.

【答案】（1）a%=1-10%-10%-20%-40%=20%，6÷10%×20%=12（人）.

補全條形統計圖如下：

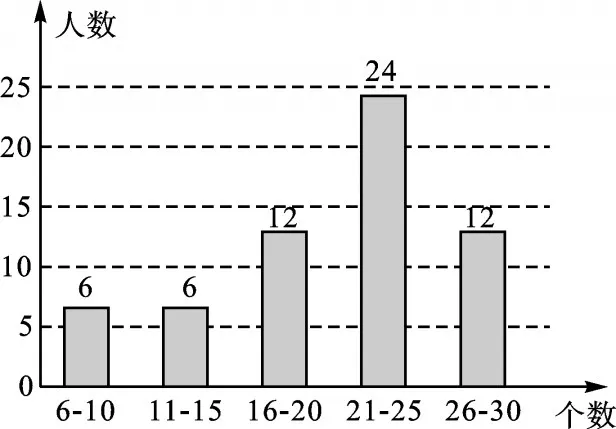
每周學習數學泰微課人數的條形統計圖

（2）解：1200×（20%+40%+20%）=960（人）.

答：該校全體學生中每周學習數學泰微課在16至30個之間的約有960人.

四、概率

例4（2017·連云港）為落實“垃圾分類”，環衛部門要求垃圾要按A，B，C三類分別裝袋，投放，其中A類指廢電池，過期藥品等有毒垃圾，B類指剩余食品等廚余垃圾，C類指塑料，廢紙等可回收垃圾.甲投放了一袋垃圾，乙投放了兩袋垃圾，這兩袋垃圾不同類.

（1）直接寫出甲投放的垃圾恰好是A類的概率；

（2）求乙投放的垃圾恰有一袋與甲投放的垃圾是同類的概率.

【分析】（1）所有等可能的結果有三個，即：A類、B類、C類，A類只有一種，根據概率公式即可求出概率；（2）列出樹狀圖，先求出所有等可能的結果，再找出符合條件的可能數，然后根據概率公式求出概率.

【解析】（1）甲投放的垃圾恰好是A類的概率是

（2）列出樹狀圖如圖所示：

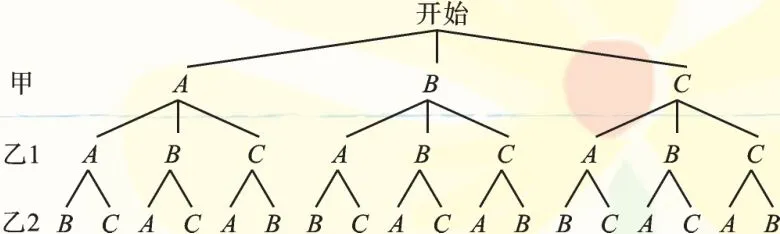
由圖可知，共有18種等可能結果，其中乙投放的垃圾恰有一袋與甲投放的垃圾是同類的結果有12種.

所以，P（乙投放的垃圾恰有一袋與甲投放的垃圾是同類）

即乙投放的垃圾恰有一袋與甲投放的垃圾是同類的概率是

【點評】一步試驗概率直接根據計算；兩步試驗概率可以用樹狀圖來解答，也可以用列表法來解答；三步或三步以上試驗概率只能用樹狀圖來解答.另外要注意是放回事件還是不放回事件，列表法或畫樹狀圖法可以不重復不遺漏地列出所有可能的結果.

【變式練習4】（2017·南京）全面兩孩政策實施后，甲、乙兩個家庭有了各自的規劃.假定生男生女的概率相同，回答下列問題：

（1）甲家庭已有一個男孩，準備再生一個孩子，則這個孩子是女孩的概率是_______；

（2）乙家庭沒有孩子，準備生兩個孩子，求至少一個女孩的概率.

【答案】（1）.（2）乙家庭沒有孩子，準備生兩個孩子，所有可能出現的結果有：（男，男）、（男，女）、（女，男）、（女，女），共有4種，它們出現的可能性相同.所有的結果中，滿足“至少有一個孩子是女孩”（記為事件A）的結果有3種，∴