秩和比法在真空濕熱定型機性能評價中的應用

舒服華

（武漢理工大學職業技術學院，湖北武漢430070）

真空濕熱定型機是生產高檔運動鞋、皮鞋所必不可少的先進設備，是冷粘鞋成型新工藝的生產設備。它采用“真空熨燙，蒸汽霧化，活化干燥，強力鼓風”等技術對繃幫后的鞋子進行時效處理，以使結幫膠干燥固化，幫面飽滿，清除繃幫過程中所產生的內應力，提高冷粘鞋的綜合性能，使鞋不易變形。真空濕熱定型機的性能和質量對制鞋生產效率和產品質量至關重要，科學評價其性能和質量對設備的設計、制造、選擇、使用具有重要的現實意義。

秩和比法 (Rank Sum Ratio，RSR)是一個內涵極為豐富的統計分析方法，它融古典的參數統計與近代的非參數統計于一體，兼及描述性與推斷性。針對性強，操作簡便，使用效果明顯[1-2]。本文利用秩和比法評價真空濕熱定型機的綜合性能，以利于提高評價的準確性和可靠性。

1 評價指標體系

XDXZ-6型真空濕熱定型機主要由箱殼部分、傳動部分、氣動部分、真空部分、加濕、加熱、置鞋箱、電器控制等主要部件組成。傳動通過電磁制動、電機、減速機、鏈輪、鏈條帶動六個內箱運轉，內箱中裝有托桿，可把鞋置于托桿上，氣動部分通過氣缸輸入壓縮空氣帶動箱蓋開合。真空部分通過真空泵，真空管，電磁閥，濾清器，抽出內箱中氣體，形成負壓，加濕是利用壓縮空氣通過電磁閥吹入箱內形成霧。加熱是在箱蓋中裝有加熱棒，兩蓋合并后對鞋加熱。根據XDXZ-6型真空濕熱定型機的結構特點，其綜合質量評價指標體系可分為以下8個部分。

1.1 箱殼部分

要求材料性能優良，尺寸符合要求，有足夠的強度和剛度，成型工藝良好，聯接牢固可靠，外表平整，無凸起、凹陷、毛刺等缺陷，涂裝精細，顏色均勻、材料環保。

1.2 傳遞部分

要求傳動部件運動靈活，無咔阻、磕碰、發熱、冒煙等現象。傳動效率高，傳動比精確。齒輪、鏈、V帶、軸承、聯軸器等運動部件材質優良，加工精度高，潤滑性能好，耐磨損、抗腐蝕，維護維修性好，使用壽命長。

1.3 氣動部分

要求空壓機與生產工藝匹配，供氣量充足，產氣效率高，能耗少，輕量化，防爆措施完善。電磁閥、調壓閥、過濾器、油水分離器等氣動元件性能優良，工作可靠，工位轉換準確到位，氣動管線能承壓額定壓力，安全系數高，密封性能好泄漏損失少，氣動部分工作噪聲小。

1.4 真空部分

要求真空泵性能優良，抽氣能力強，抽氣效率高，冷卻循環系統運轉正常，泵體工作時溫升小，運動部件潤滑優良，磨損小真空管材質量優良，耐高壓，耐高溫、耐腐蝕、耐磨損，真空儀表,真空閥門等控制元件工作可靠，真空度控制精確。真空部分密封性能好，噪音小。

1.5 置鞋箱

設計合理，有充足的承載能力，內部無塌陷、彎曲、扭曲變形，無剝落、斑禿、飛邊等缺陷，箱門開關靈活，密封性好，單位容積鞋容量大，材料耐高溫、耐高壓、耐腐蝕、耐磨損。

1.6 加濕部分

加濕元件工作可靠，加濕迅速，濕度分布均勻，濕度控制精度高，節水，加濕動作精準，關停自如，管線密封性好，無滲漏開裂現象，材料耐腐蝕、防潮防銹。

1.7 加熱部分

加熱元件質量優良，升溫迅速，溫度分布均勻，熱傳播效率高，節能，溫度控制精準，系統安全可靠，耐高溫、無燙傷、火災、觸電等隱患。

1.8 電氣控制系統

電機功率因素高，防潮防爆，接地保護和漏電保護好，電氣控制箱穩固結實，操作方便，絕緣性能好，線路布置符合規范，導線容量足夠，繼電器、接觸器，斷路器等電氣元件性能優良，工作可靠，安全系數高。

2 秩和比評價方法

2.1 基本原理

RSR法是一種有效的多指標評價方法。秩和比法的基本思想是在一個n行(n評價對象)m列(m個評價指標)矩陣中，通過秩轉換，獲得無量綱的統計量RSR，以RSR對評價對象的優劣進行排序或分檔。評價對象的RSR越大，則越優。該評價方法計算簡單，對數據信息要求低，抗干擾能力強，并可與其他許多數理統計方法互相溝通、移植和嫁接[3、4]。

2.2 評價步驟

2.2.1 數據規范化處理

對于傳統的秩和比，不需要對數據進行規范化，不論何種量綱和數量級的數據，只需按數值的大小編秩即可，但對于加權秩和比，由于屬性之間的量綱和數量級不同，對求權有一定的影響，因此需要對原始數據進行規范化處理。屬性指標一般分為二類：效益型指標、成本指標。所謂“效益型指標”就是指標值越大越好；“成本型指標”則是指標值越小越好[5]。對于不同類型的指標，數據規范化方式不同。

當xij為效益型數據時，數據規范化方法為：

當xij為成本型數據時，數據規范化方法為：

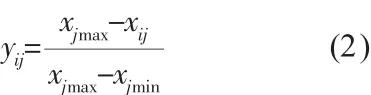
式中，xij為原始數據，yij為規范化數據；xjmin=min{xj1，xj2，…，xjn}；xjmax=max{xj1，xj2，…，xjn}。(j=1,2，…，m)。

2.2.2 確定指標的權重

評價對象綜合性能為各評價指標性能的線性組合。由于各指標對其綜合性能的重要程度不同，因此需要以權重的形式體現。文中以客觀的熵值法確定權重。在信息論中，熵是對不確定性的一種度量。信息量越大，不確定性就越小，熵也就越小；反之，不確定性就越大，熵也就越大。這樣可以通過計算熵值來判斷某個指標的離散程度，指標的離散程度越大，該指標對綜合評價的影響越大，所賦予的權重就越大。熵值法確定權重的具體步驟如下[6、7]：

(1)計算指標的比重

(2)計算指標的熵值

式中，k=1/lnn對于特殊情況當Pij=0時，取 lnPij=0。

(3)計算指標的差異系數

(4)計算指標的權重

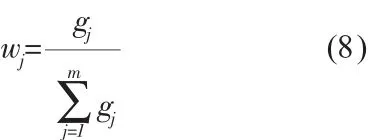
式中，Pij第 i評價單元第j指標的比重；ej第j個指標的熵值；gj第 j個指標的差異系數；wj第j個指標的權重(i=1，2，…，n；j=1，2，…，m)。

2.2.3 編秩[8]

編秩就是對每個評價對象的每個指標在同類中的優劣程度進行排序，即根據評價值對評價矩陣X=(xij)的每一列元素進行比較排出優劣次序。對于效益型指標從小到大編秩，成本型指標從大到小編秩，同一指標數據相同者編平均秩，秩越大表明屬性值越優。對于數據已經規范化處理的評價矩陣Y=(yij)，直接按第一種情況編秩，由此將評價矩陣轉化為秩矩陣，記為R=(rij)。

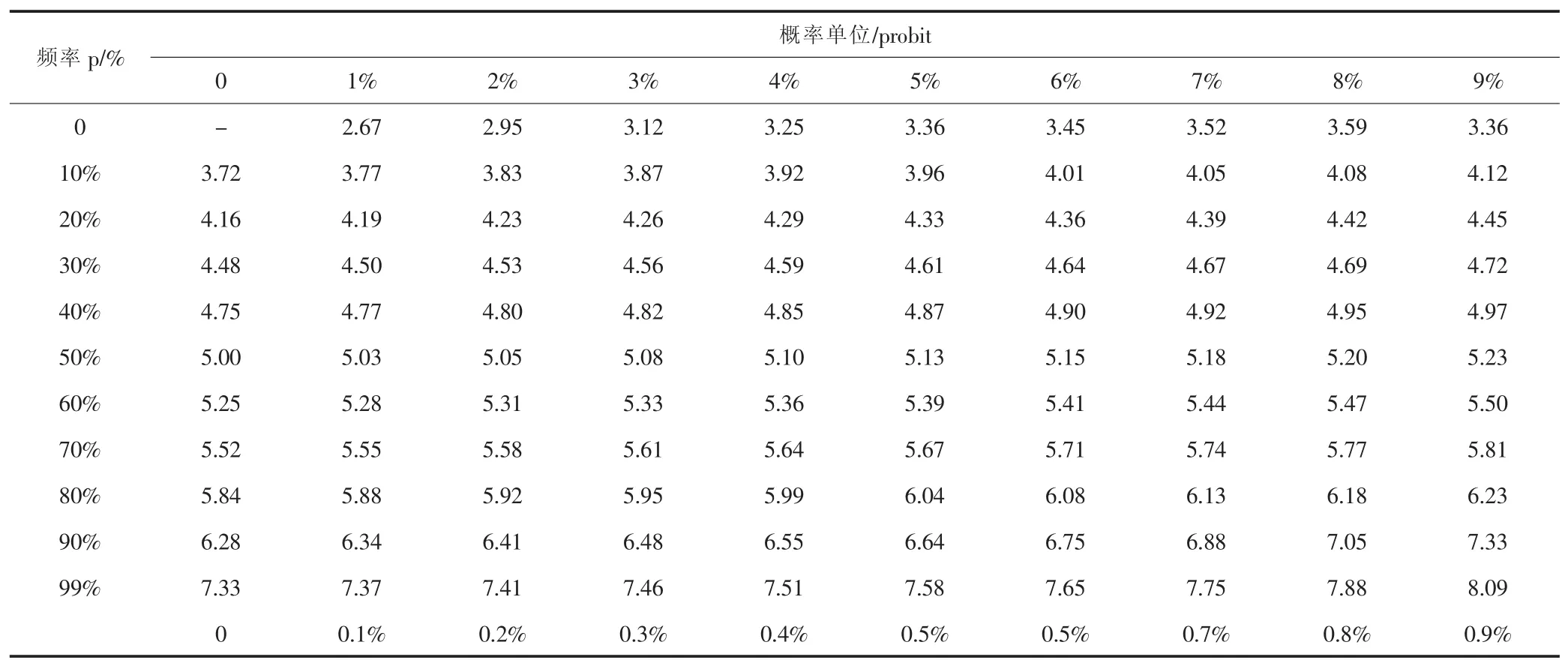
表1 p(百分率)與概率單位(probit)對照值

2.2.4 計算秩和比

秩和比指的是矩陣中行(或列)秩次的平均值，是一個非參數計量，具有0-1區間連續變量的特征。計算公式為

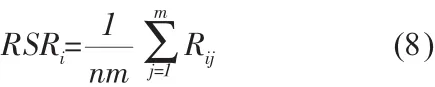
式中，RSRi為第i個評價對象的秩和比；Rij第i個評價對象的第j指標的秩，(i=1，2，…，n；j=1，2，…，m)。

當各評價指標的權重不同時，評價對象的秩和比為各指標秩的加權和。計算公式為：

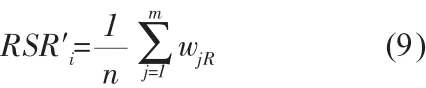
式中，RSR’i為第i個評價對象的加權秩和比；wj為第j個評價指標的權重，∑wj=1，(i=1，2，…，n；j=1，2，…，m)。

2.2.5 確定R SR的分布

雖然通過秩和比可以對評價對象進行排序，但這種排序是否有效或者可靠，是否有其他干擾因素影響了評價的結果，還需要進一步分析。分析的基本方法是進行統計回歸。確定RSR的分布是重要的一步，其的任務是計算評價對象的概率單位值(probit)。首先編制RSR頻率分布表；列出各組頻數fi；計算各組累計頻數∑fi；然后確定各組RSR的平均秩次R；最后計算向下累計頻率pi(以百分率計)；最后一個累計頻率按1-1/(4n)估計，將pi轉化為評價對象的概率單位probit。計算公式為

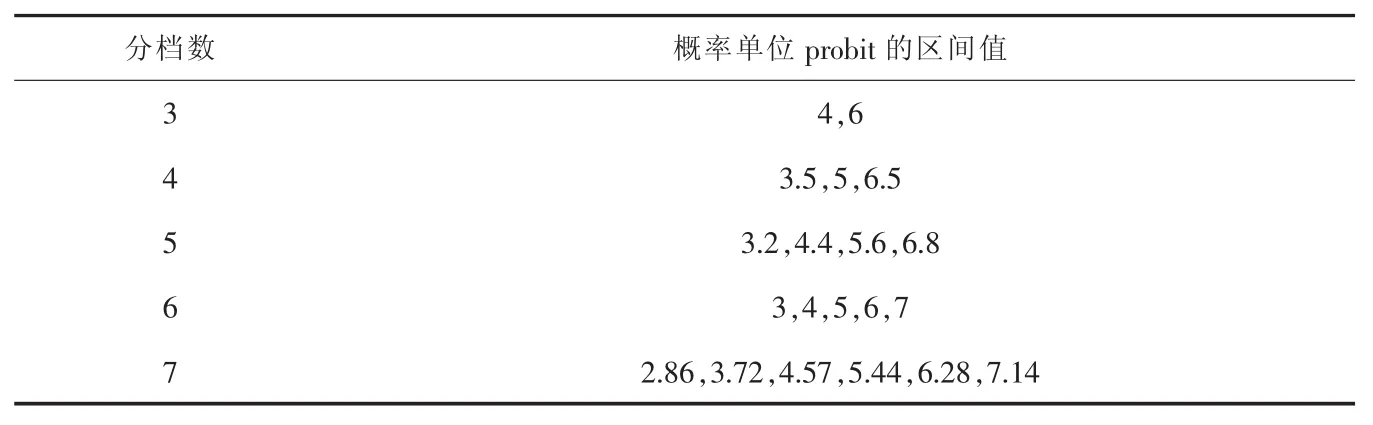
表2 常用的分檔類型與概率單位值

表3 待評價真空濕熱定型機的性能指標值

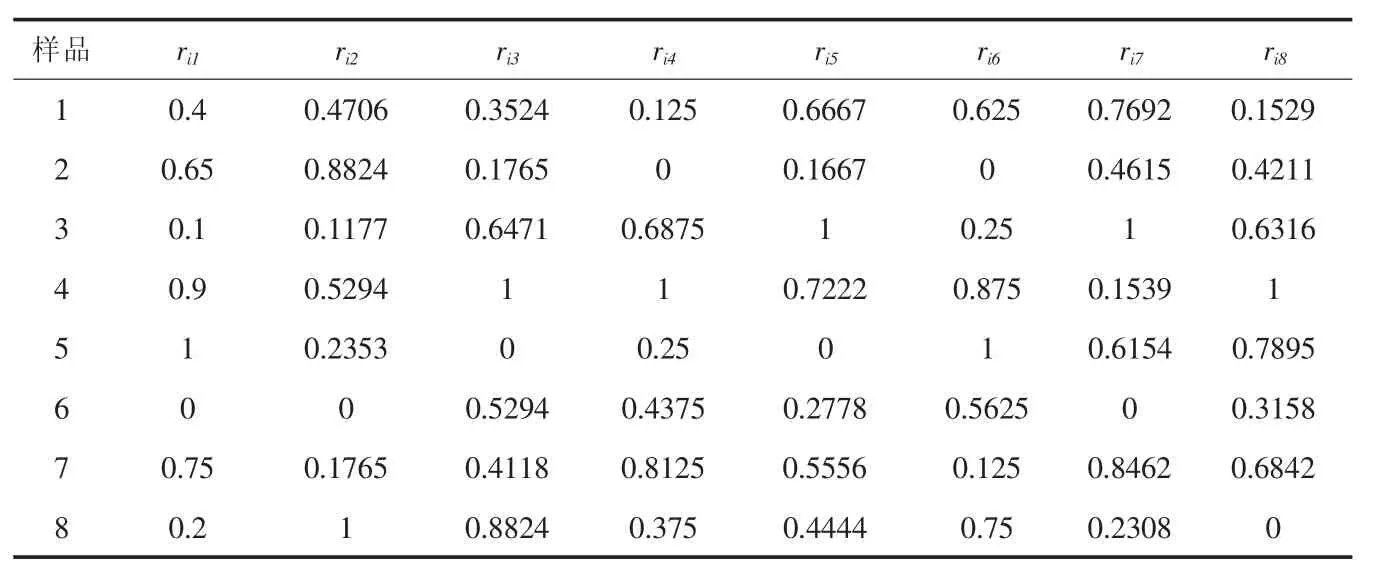
表4 數據規范化結果

式中，pi為第i評價對象向下累計頻率；probiti為第i評價對象的概率單位值；u(·)表示pi的標準正態離差函數。

常用的p與probit值的對照表如表1所示，表中第1行和第1列對應值的和為百分率值pi，交叉處為相應的概率單位probit值，最后第1行和最后第1列對應值的和為99%以上百分率值pi，表中probit值以通過公式(11)的轉化，可以直接通過pi查找對應的probit值。

2.2.6 計算回歸方程

以累計頻率pi對應的概率單位probiti值為自變量，秩和比RSRi為因變量，構造一元線性回歸方程，目的是檢驗RSR法排序可信度，設一元直線方程為[8]

式中，a、b為回歸方程的系數。

求出a、b和其他參數，據此對模型進行分析。

2.2.7 分檔排序

根據回歸方程計算得到的秩和比值，對評價對象進行分檔排序。分檔的依據是標準正態離均差u，常用的分檔數為3～7檔，其分別對應的概率單位probit值如表2。確定分檔數量后，依據其對應的概率單位Probit臨界值，根據評價對象的秩和比值進行分檔。

2.2.8 模型的檢驗

(1)擬合優度檢驗(R2檢驗)

它是檢驗模型對樣本觀測值的擬合程度，指標為關聯系數R2，R2越接近于1，說明實際值與預測值越接近，擬合優度越高，一般 R2＞0.7。

(2)顯著性檢驗

它是檢驗自變量是否對因變量有顯著線性影響。分為F檢驗、t檢驗、P檢驗，當要求 F＞F0.025(1，n-2)；t＞t0.95(n-2)，P＜P(0.25)=0.05時顯著線性姣好。模型的顯著性越高，評價的可靠性越大，評價模型越有效。

3 應用實例

以8臺XDXZ-6型真空濕熱定型機為研究對象。分別記為 S1、S2、S3、S4、S5、S6、S7、S8，選取箱殼部分、傳統部分、氣動部分、真空部分、加濕系統、加熱系統、置鞋箱、電氣部分8項性能參數作為評價指標，分別記為 C1、C2、C3、C4、C5、C6、C7、C8。8 臺真空濕熱定型機的8項性能指標檢查結果如表3所示。

對真空濕熱定型機屬性指標數據進行規范化處理，其中，真空濕熱定型機技術性能的8個指標全部為效益型數據，按式(1)進行規范化處理，結果見表4。

計算每個屬性指標的權重。首先按式(5)計算各個指標的比重，結果如表5所示，然后按式(5)～(6)計算每個指標屬性的熵值、差異系數，最后按式(7)計算每個屬性指標的權重，結果見表5。

真空濕熱定型機8個性能指標的權重分別為:

wj=(0.12918，0.12987，0.12147，0.12 562，0.12191，0.12530，0.12439，0.12224)

根據表5中數據，對每臺真空濕熱定型每個性能指標進行編秩，8臺真空濕熱定型機8個屬性的秩次如表6。然后按式(9)計算加權秩和比，結果如表6。

此時，可以按照秩和比對8臺真空濕熱定型機的綜合質量進行排序(結果見表7中的第一列)，根據秩和比大小8臺真空濕熱定型機綜合質量由優到差的次序為：S4、S7、S3、S5、S8、S1、S2、S6。S4綜合質量最好，S6綜合質量最差。秩和比評價結果見圖1。

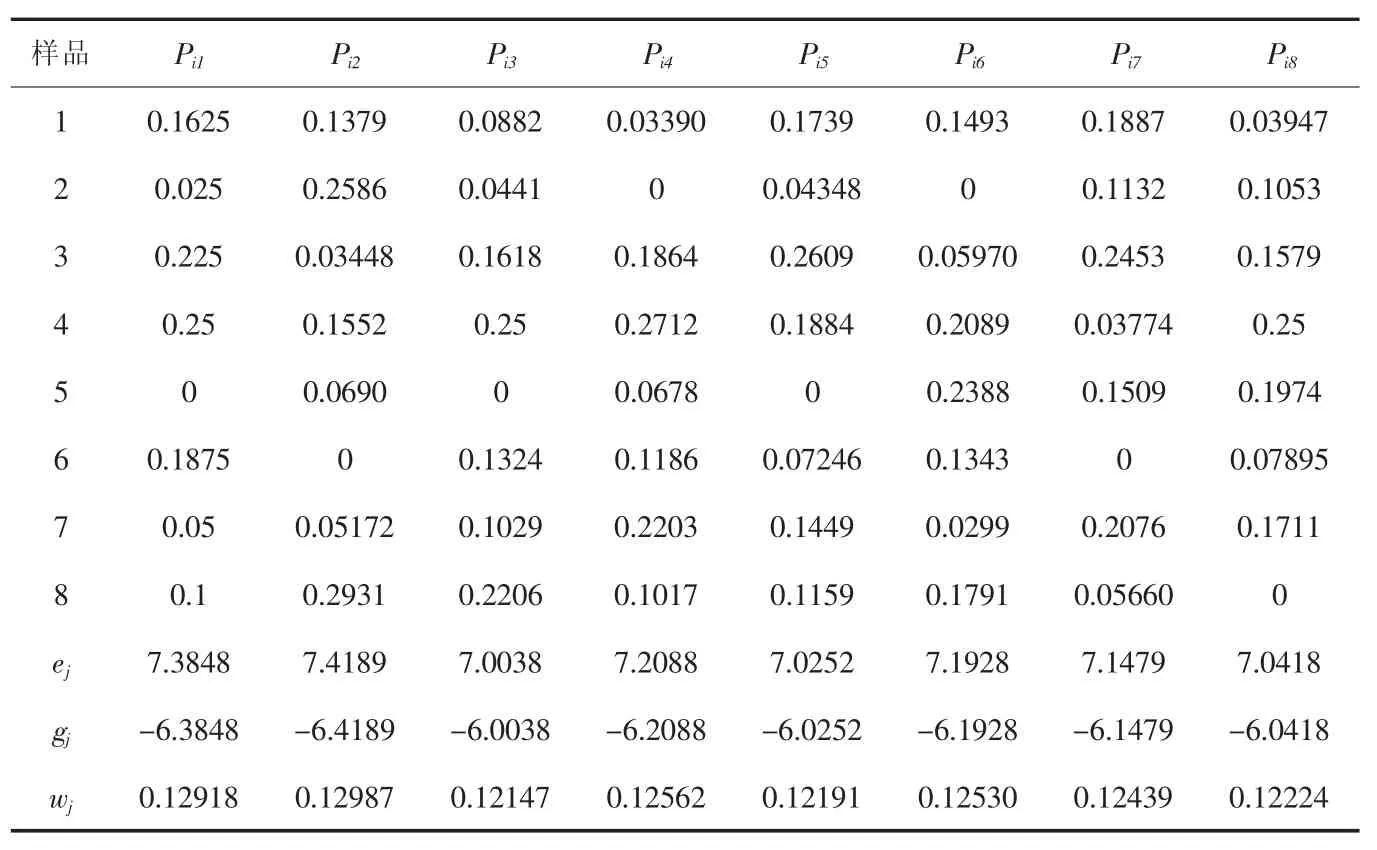
表5 評價真空濕熱定型機性能指標的權重數據

雖然這8臺真空濕熱定型機的RSR值不同，但并不意味這些不同是有顯著性的，或許因其他噪聲因素的加入影響了RSR值，證明評價的真實性度也就不能令人信服，所以應該進行假設檢驗。此外，我們不僅希望要獲得真空濕熱定型機質量直觀的印象，還希望知道它們更為詳細的信息，因此對模型進行回歸分析。首先按式(7)計算每個評價對象向下累計頻率pi；然后按表1轉化為概率單位，結果如表7。

以表7中的概率單位為自變量，秩和比為因變量，建立如式(12)的一元線性方程，求得系數如表8所示。即a=-0.18158，b=0.14224。

一元線性方程為：

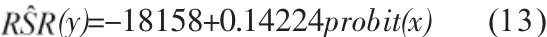
對回歸方程進行檢驗，求出得R2、F、t、p及誤差的方差σ，結果如表8。

從表8知，R2=0.93654，說明模型的相關 性 很 大 ，F=88.545＞F0.025(1，6)=8.81；t=9.409＞t0.95(6)=1.943、p=0.00008＜P(0.25)=0.05、σ=0.0015，很小，這些數據說明了模型具有極高的顯著性，該秩和比模型對評價真空濕熱定型機的性能有效，結果可靠。

一元線性回歸模型的預測值如表7。一元線性回歸方程見圖2。

根據一元線回歸方程計算得到的秩和比值，對評價8臺真空濕熱定型機進行分檔。由于8臺真空濕熱定型機的最大小于 9，最小大于3，根據分檔法則，分為3檔比較合適，可將三個擋次的級別定義為“優秀”，合格”，“不合格”。分檔結果為：S3、S7、S4屬于“優秀”等級；S2、S1、S8、S5屬于“合格”等級；S2屬于“不合格”等級。根據不同檔次概率單位probit值范圍，按式(13)求出相應的RSR的范圍結果見表9。

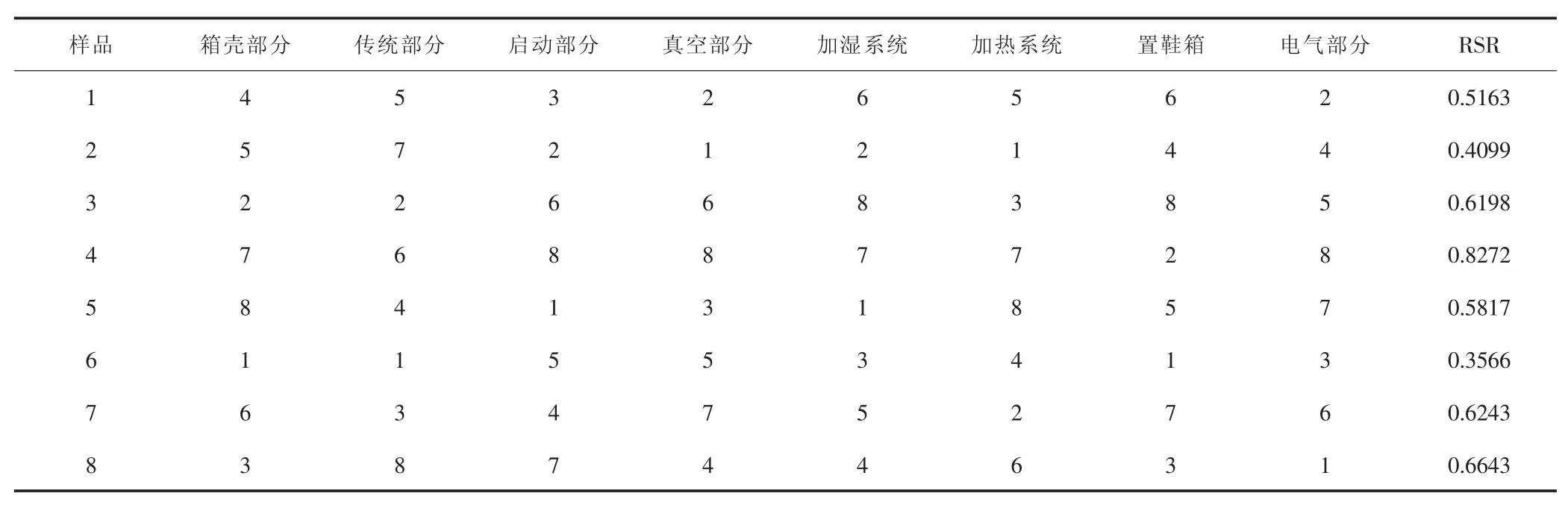
表6 評價真空濕熱定型機屬性的分布及秩和比

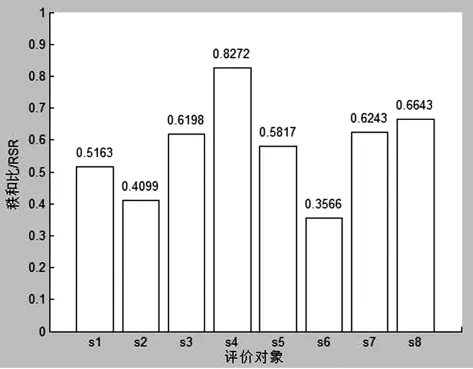
圖1 真空濕熱定型機評價結果

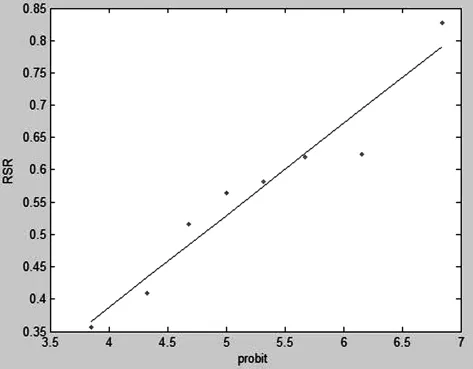
圖2 一元線回歸方程圖

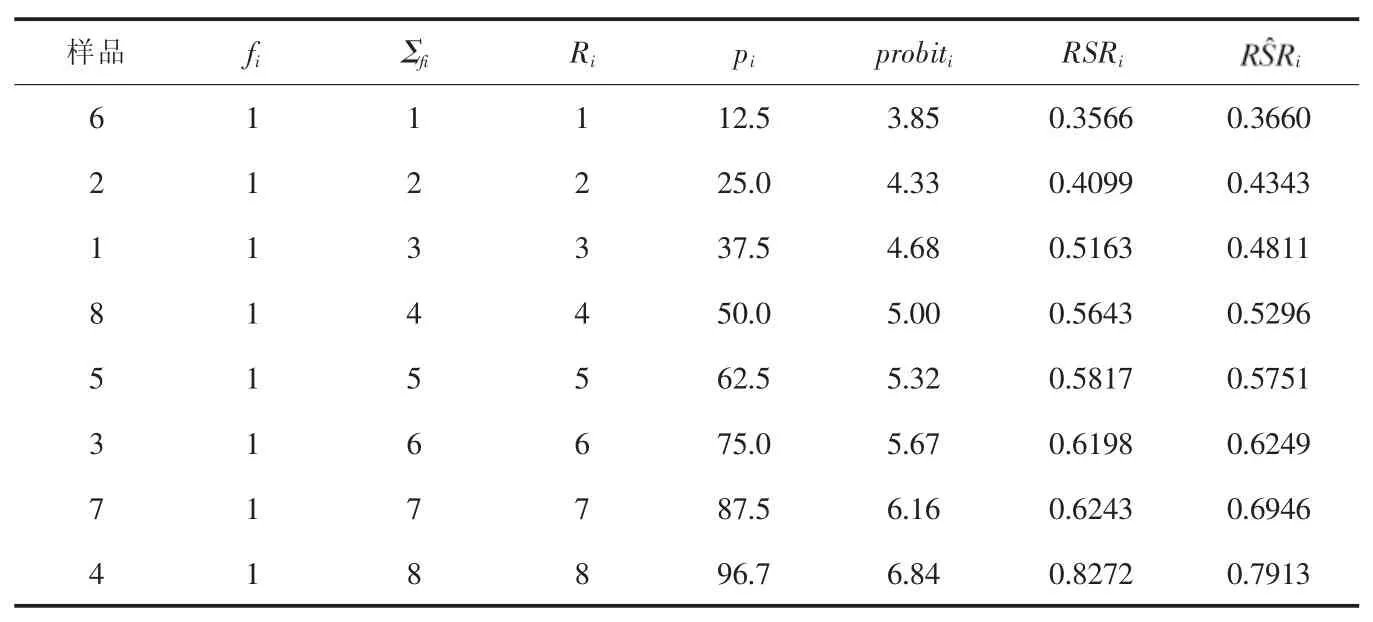
表7 評價的秩和比分布數據

表8 秩和比一元回歸方程參數

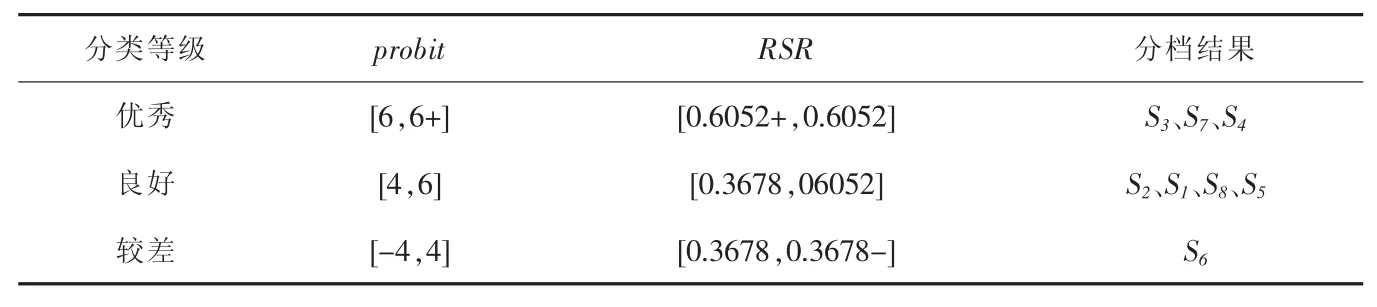
表9 真空濕熱定型機分檔情況

4 結語

真空濕熱定型機是皮鞋生產的重要設備，它的性能和質量關系到制鞋工藝的成敗和質量的優劣，客觀評價真空濕熱定型機的性能和質量，是保證選擇優良設備和維持生產順利進行的基礎。秩和比法是一組全新的統計信息分析方法，是數量方法中一種廣譜的方法，被廣泛用于各領域的質量綜合評價。秩和比法操作簡便，對數據信息要求不高，既可以對評價對象進行排序，還可以對評價對進行分檔，豐富了評價的內容，不僅能讓人感受到直觀的印象，還能讓人挖掘出更多隱藏的深層信息，是多屬性問題決策的有效工具。文中運用秩和比法對真空濕熱定型機綜合性能進行了評價，取得了良好的效果，模型有較高的相關性和顯著性，能有效提高評價結果的可靠性。

[1]朱干江,王桂芝,趙靖.科技進步綜合評價中秩和比法的運用[J].科技進步與對策,2007,24(6):51-54.

[2]付維華,付堯,李文帥.秩和比法(RSR 法)在環境污染健康損害中的應用 [J].廣州化工,2012,40(3):101-103.

[3]陶莊.經典秩和比法詳解[J].數理醫藥學雜志,2007,20(2):122-125.

[4]顧潔,王春義,牟宏.秩和比法在高壓配電網項目評價中的應用 [J].電力科學與技術學報,2015,30(1):80-86.

[5]付學謙,陳皓勇.基于加權秩和比法的電能質量綜合評價[J].電力自動化設備,2015,35(1):128-132.

[6]金晶,張研,劉文俊.基于加權秩和比法的麻城市鄉鎮衛生院服務能力綜合評價[J].中國衛生事業管理,2016,(4):246-249.

[7]王天營.一元線性回歸分析中三種檢驗的等價性研究[J].統計與決策,2011,(3):8-11.

[8]張敏靜,劉雅娜,薛志群.一元線性回歸方程有關檢驗問題的研究[J].價值工程,2012,(2):1-2.