初中學生在不等式部分的學習問題探究

汪秀云

(福建省南平市浦城縣仙陽中學 353409)

不等式部分內容是初中數學教學的重要組成部分，也是初中數學的教學難點，很多學生在學習中存在諸多問題，一是因為該部分知識本身難度所致，還有一方面是學生首次接觸不等式，在解題方法和知識理解上有所欠缺，這些都導致了初中生在不等式部分學習困難的情況.

一、初中生不等式部分知識學習維度

1.記憶學習維度

記憶是學生學生學習的基礎，通過該維度的學習，學生能夠對不等式的概念、不等式的關系和不等式的性質進行記憶，能夠知道不等式符號的改變條件.能夠達到這一學習維度的學生，一部分學生能夠解決一些不需要推理的問題，能夠借助不等式的定義來求解問題，如例1之類的問題.還有一部分學生能夠解決一些關于不等式程序性記憶要求較高的問題，這類問題不需要過多的推理，只要通過去分母、移項就可以完成求解，如例2之類的問題.

例1：從下列式子中挑選出不等式：-5x<0;5x+5>0;x=-8;y≠8;x-7≥0.

對于這樣的問題只需要根據不等式的定義，一個一個往里套就可以，只要不符合條件要求的都可以舍去.

例2 解不等式：2x-2≥4x.

2.解釋學習維度

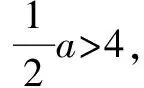
3.探究學習維度

探究性學習是學生學習達到一定高度，能夠解決一些非常規的問題，能夠對某一數學問題進行創造和改造，創造性的解決某一數學問題.首先，能夠從問題背景中找出蘊含的數學不等式關系，找出解題的突破口.其次，能夠根據題目信息，建立不等式模型.例如，某服裝廠有甲布料38米、乙布料26米，打算用這些布料制作A、B兩款衣服，其中A款衣服需要甲布料0.5米，乙布料1米，可以產生45元的利潤；B款衣服需要甲布料0.9米，乙布料0.2米，可以產生30元的利潤；其中生產A款衣服的數量為x，兩種款式獲得的總利潤為y.

(1)寫出x、y的關系方程，并寫出x的取值范圍.

(2)該批次需要生產多少A款的衣服才能夠使的服裝廠的利潤最大化？最大利潤是多少？

干預前兩組心理狀態評分均差異無統計學意義（P>0.05），干預后觀察組的HAMA與HAMD評分均顯著低于對照組（P＜0.05），見表 2。

這個問題從本質上來說就是一個建立函數模型、解決函數模型的過程.

二、初中生不等式部分學習存在的問題

1.不等式關系方面

2.不等式性質方面

不等式的性質主要包括三個方面，第一，在不等式兩側都加上或者減去同一個整式，不等式的不等號方向不變；第二，在不等式兩側同時乘以或者除以一個正數，不等式的不等號方向不變；第三，在不等式兩側同時乘以或者除以一個負數，不等式的不等號方向改變.通過學生在平時的練習發現，學生對于該部分知識的掌握相對較好，僅有極少數學生對該部分知識掌握存在問題，由此可見，該部分知識難度相對較低.從存在的問題來看，這極少數的學生對不等式性質的理解不夠透徹，僅僅停留在不等式的基本性質的記憶上，對于等式的性質和不等式之間的性質不能夠靈活轉化，知識的遷移能力較差.例如下列練習題：

下列不等式變形的依據是：

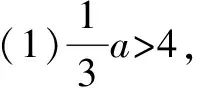
(2)a-9>0,得出a>9

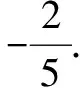
例：如果a

在證明B不等式的時候，學生往往只顧著兩側乘以b去約分，忘了b<0這一先決條件，導致出錯，證明C存在的問題和B一樣，都忽視了字母中隱含的符號關系.

3.不等式解集方面

在這一方面，學生存在的主要問題就是對“一個解”、“唯一解”、“解集”、“解”的把握不準確.尤其是在“解”和“解集”的概念上，沒有把握好.造成這一因素的主要原因就是學生對這些概念把握不到位，另外，不等式的解與方程的解相類似，學生沒有準確的把握兩者之間的區別，這才導致了錯誤的產生.

4.不等式組方面

涉及到該部分知識的問題，一般情況下對學生的計算能力要求較高，在平時的練習中，出現問題的學生主要是計算錯誤.有的學生在移項的時候沒有改變不等號的方向，還有些學生就是對不等式性質把握不當，應用過程中出現問題.

例如：解下列不等式組，并在數軸上表示出來.

5.一元一次不等式和一次函數方面

通過對學生平時的練習可以看出，學生對于該部分不等式的求解更偏向于運用代數的思維來做，盡管有些問題只需要通過函數圖像就可以明顯的看出，學生依然選擇復雜的代數法.如果學生采用函數圖像的方法來求解，就需要仔細認真，尤其是在符號變化上要注意.相比較于函數圖像法來求解，代數法不涉及到不等號的變換問題，學生出錯的幾率更低一些.

例1 一次函數y=2x-4交x軸與(2，0)一點，那么一元一次不等式y≤0的解集是？

A.x≤2 B.x<2

C.x≥2 D.x>2

在利用函數圖像法解這一題的時候，部分學生在將坐標系中y<0時，x的取值范圍轉化為代數時出現錯誤，圖像中的解集是x≤2,當換成代數時不等號的方向卻反了.

初中學生對于不等式部分知識的學習可以分為三個理解水平，學生的記憶和解釋學習水平較高，但是探究性學習水平較低，導致學生在解決常規性問題的時候能夠游刃有余，一旦涉及到創新性問題就不知從何下手.另外，學生在不等式部分的學習中經常存在遷移錯誤、表征錯誤和取之錯誤的問題，這些問題涵蓋了不等式部分的所有內容，需要教師在教學中加以重視.

參考文獻：

[1]彭明菊.關注過程·豐富經驗·提升品質——以“不等式的概念”教學為例[J].新教育,2014(02):51-52.

[2]閆建明.淺談關于方程(組)、不等式(組)、函數等初中數學模型的教學及應用[J].新課程學習(中),2013(04):46-47.