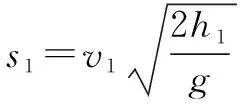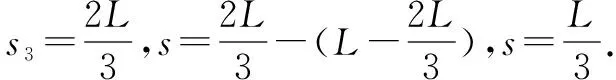由一道錯誤的平拋運動習題引起的思考
楊紫涵
(江蘇省溧陽中學高一14班 213300)
在學完平拋運動以后,我們的作業中有這樣一道題:某學生做飛鏢游戲,前后將兩只一樣的飛鏢a、b由相同的位置水平扔出,飛鏢水平投擲的初速率va>vb,不考慮空氣阻力影響,則a,b兩飛鏢打在豎直靶上的情形(側視圖)可能是圖1中的 ( ).

圖1
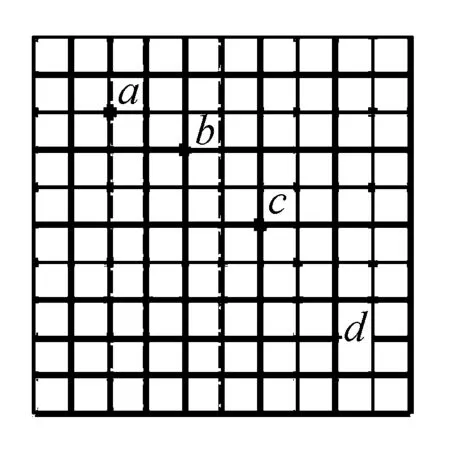
分析思路因為兩只飛鏢運動的水平位移是相同的,根據x=v0t,又因為va>vb,所以ta 解題感受初看起來上面的分析完全符合一般同學的想法,但仔細一想本題存在一問題,因為飛鏢是水平投出的,同時又不考慮空氣阻力的影響,所以飛鏢只能水平打在靶上,也就是題目中的側視圖是錯誤的.由此,我們在學習平拋運動時,必須注意這么幾個問題. 我聯想到上課學案中有一道題: 圖2 在探究平拋運動規律的實驗中,用印有小方格的紙來記錄實驗中小球的軌跡,邊長l=1.25cm的小方格記錄了小球在平拋運動過程中的若干個位置,如圖2a、b、c、d所示,根據題目所給條件,則可知小球作平拋的初速度的表達式為v0=____(用l、g表示),其數值是____.(g=9.8m/s2) 分析思路許多同學錯誤認為這一題是有問題的,因為作平拋運動的物體在豎直方向作初速度為零的勻加速運動即自由落體運動,那么在連續相等時間內位移大小之比應該是1:3:5:7…,而題目中在豎直方向的位移之比則為1:2:3,從而認為題目有問題.實際上只要在豎直方向相臨相等時間位移之差是一個定值,就說明豎直方向是加速度是恒定的,那么為什么兩個位移大小之比的結果不一樣呢?其實這個問題很好解釋,主要是后面的位移大小之比不是從開始比的,也就是說a點并不是平拋運動真正的起點.本題有兩種解法. 方法一:利用Δy=gt2,即l=gt2, 解題感受從上面分析不難看出,善于抓住平拋運動水平和豎直方向的運動特點,不僅能正確快速解題,而且能夠解釋看似矛盾的問題. 我平時喜歡打乒乓球,其實這里面也包含了平拋運動的知識. 已知乒乓球的球臺長2L、球網的高度為h,乒乓球與球臺碰撞前后水平方向速度大小不變,豎直方向的速度大小不發生變化、但方向變為相反,假設不計乒乓球的轉動和空氣的阻力影響.求: (1)若乒乓球在臺子的邊緣O點高度為h1的正上方處以水平速度v1發出,乒乓球掉在球臺的P1(如圖所示實線),求P1點距O點的距離s1; 圖3 圖4 (2)若乒乓球在O點的正上方以水平速度v2發出,球剛剛好在運動的最高位置點時擦過球網掉在球臺的P2點(如圖3所示虛線),求v2的大小; (3)若球在O點正上方某點水平發出后,球經球臺反彈后正好擦過球網且恰好落在對方球臺的邊緣P3位置處,求發球點距O點的高度h3. 解(1)如圖3所示,發球后乒乓球飛行時間t1落到球臺,根據公式 s1=v1t1② 解題感受通過第(3)問的兩種解法,很明顯直接利用自由落體運動在豎直方向的運動特點,通過推理很快就能得出結論,避免了復雜的計算. 關注斜面上的平拋運動 平時做的平拋運動的題目與斜面有關的也不少,先來做一個歸納總結. 圖5 從運動學層面上看平拋運動是在我們學習了勻速直線、勻變速直線運動之后所學的第一種曲線運動,平拋運動的處理方法并不是從數學上研究軌跡方程,而是采用化繁為簡,化曲為直,即分解運動的辦法.從這個層面上看又和前面所學的力的分解有聯系,實際上是對描述運動的位移、速度的分解.當然矢量的分解都遵循平行四邊形定則.對于斜面上的平拋運動,我們更要熟練運用相關的公式、推論靈活解決這類問題. 最后,本人在撰寫論文過程中,江蘇省溧陽中學史文杰老師給予了充分的指導,在此表示感謝! 參考文獻: [1]人民教育出版社,課程教材研究所,物理課程教材研究開發中心.普通高中課程標準實驗教科書物理2必修[M].北京:人民教育出版社,2010. [2]莫洪祥.淺談平拋運動的規律及應用[J].中學物理教學參考,2010(5). [3]李燕燕.關于平拋運動的研究[A]. 《現代教育教學探索》組委會.2013年4月現代教育教學探索學術交流會論文集[C].《現代教育教學探索》組委會,2013(2).