在線視覺測量系統的刀具圖像去抖動方法研究*

杜文華 楊 芳 曾志強 王俊元 段能全 王瑞倩 楊 揚

(①中北大學機械與動力工程學院，山西 太原 030051；②繁峙縣環保局，山西 繁峙 034302)

在現代制造業中，產品的外觀設計和質量同等重要，機器視覺技術因具有非接觸、動態測量、高精度等特點，廠家在產品包裝中的視覺檢測應用日益廣泛。在復雜工業環境中，生產過程中如產品噴碼等操作、生產線機械傳動引起的傳送帶抖動等干擾因素導致圖像抖動問題，而機器視覺檢測系統的圖像質量直接關系到檢測精度和該系統的價值，因此解決動態高精度視覺系統中圖像抖動問題具有重要的理論意義和工程實用價值。

視覺檢測系統是在外設硬件的基礎上兼顧算法來實現圖像數據信息的采集和處理的。國內外科研實驗室和制造企業已經對圖像消抖和圖像去模糊問題進行了相關的研究，王智峰等人提出一種各向異性非線性擴散的圖像消抖算法。他們對圖像內部點和邊界點進行并行處理，利用抖動誤差值達到最小的方法去估計抖動偏差[1]。接著，錢翔等人采用自組織映射網格分類圖像的色彩空間，分割提取每一幀的圖像結構，利用連續兩幀的分割結果的二維相關函數去計算幀間的偏移，消除整個圖像序列的抖動[2]。隨后，馮澤、周圓圓等人分析了圖像去抖動模型存在的問題，對抖動模糊核進行估計，對金字塔模型結構進行布局，實現了R-L反卷積算法改進的圖像去抖動模糊處理研究[1，3]。現有圖像復原算法多數是在R-L反卷積算法的基礎上進行改進，目前存在以下4個問題：(1)存在振鈴效應；(2)耗時性；(3)圖像的質量復原的評價方案有待進一步改良；(4)實驗驗證效果不佳。

針對以上問題，本文從圖像消抖算法出發，對比分析現有圖像復原方法，在自適應R-L算法的基礎上，結合金字塔模型，研究一種兩者相結合的去抖動方法，同時在現有質量評價方法的基礎上增加圖像復原相關測度和效應時間兩個參數對復原圖像進行評價，最后以實驗室的視覺測量系統平臺對算法的實現進行實驗驗證，實現抑制振鈴效應、縮短計算時間、完善圖像質量評價方法和實驗驗證效果的多重目標。

1 圖像消抖模型

R-L算法及其改進的一系列算法均是基于貝葉斯概率框架下的描述，在圖像去模糊研究中廣泛應用。其中圖像抖動模糊模型可以表達為：

B=I?K+n

(1)

式中：?為卷積操作符；B為模糊圖像；I為潛在的原始圖像；K為模糊核；n為噪聲。

在這個框架下，對PSF核進行估計，利用圖像復原方法對模糊圖像進行復原，生成高質量的重建圖像。為了更好地提高去抖效果的基礎框架和減少應用時間，使用改進R-L算法兼顧金字塔布局的方法，對采集到的圖像利用核估計和去模糊過程。圖像消抖模型的總體框架如圖1。

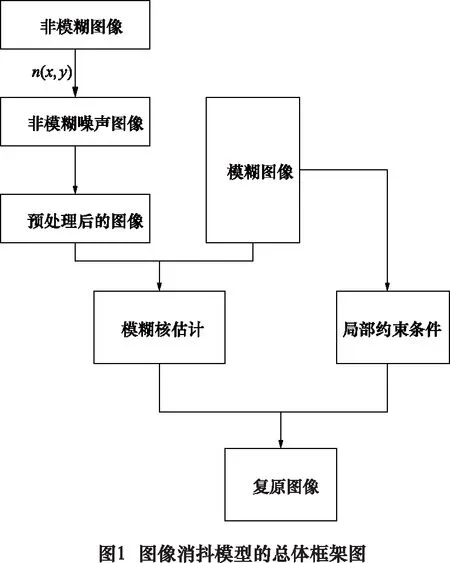
2 算法理論及方法構造

根據貝葉斯理論，推導出L-R算法的迭代復原圖像公式：

(2)

式中：It+1、It分別是第t+1次迭代和第t次迭代的復原圖像的估計值；K表示模糊核；B表示模糊圖像。

由式(1)可知復原算法兩次迭代之間存在殘差：

ΔIt=I×K-K×IT+n

(3)

式中：ΔIt為每次迭代的殘差；n為噪聲。

由式(3)可知，當噪聲影響無法忽略不計時，此算法每次迭代存在噪聲放大和振鈴效應的現象。為了避免每次迭代過程中的噪聲放大現象和減小振鈴效應，我們采用新的數學模型代替算法式(2)：

(4)

式中：q(x,y)=λEσ×I0,I0為迭代的初始圖像；Eσ為高斯濾波器；為梯度；λ為相關系數。

金字塔思想：圖像金字塔是一種分辨率逐層減小的形狀排列布局，一副圖像金字塔是利用分辨率詮釋圖像的一系列圖像集合[12]。塔的底部是用要處理圖像的高分率表示，頂部是低分率近似。圖像金字塔結構是一種與降采樣和平滑操作相結合的圖像表示方法，其優點是每層的像素數量從底部到頂部逐層減少，從而使計算量驟減。

算法式(4)解決每次迭代存在的噪聲放大和振鈴效應現象；但反復迭代導致計算時間增加。為了解決振鈴效應、噪聲放大和計算時間的多重問題，將此算法結合金字塔思想，對同一幅圖像分區分頻處理。基本思想：將一個模糊圖像分出高低頻的邊緣區域和平滑區域，金字塔的低端為高頻邊緣區域，逐漸過渡到金字塔的頂端低頻平滑區域；在圖像邊緣區域，用算法式(4)，因為此區域是灰度劇烈化的區域，此時Eσ×I0→0，用算法式(4)的作用相當于對It進行復原算法后再使用一次低通濾波，以減弱高頻部分，進而使圖像在高低頻間平滑渡過；在圖像平滑區域，用算法式(4)，此區域灰度變化平緩，Eσ×I→0，此時算法式(4)和算法式(2)兩式相同，相當于對于低頻平滑區域用算法式(2)。

3 圖像去抖動處理仿真實驗結果分析方法

逆反卷積法、維納去卷積、R-L算法和本文方法這4種圖像去抖動的效果好壞需要一種評判標準。下面闡述圖像去抖動的圖像質量評判方法，通過這幾種評判標準分別對這4種去抖動方法進行性能參數比較，評估不同的處理結果。

3.1 圖像去抖動的質量評判方法

算法實現的效果是通過主觀觀察評價和客觀參數評價兩方面進行評價的。主觀評價圖像質量分五類：特別好、比較好、一般、比較差和特別差，對應分值分別是5、4、3、2、1。客觀參數評價主要有：均方誤差(MSE)、峰值性噪比(PSNR)、灰度平均梯度法(GMG)、拉普拉斯算子和法(LS)、圖像復原相關測度(K)和計算時間(T)等[15-16]，其中MSE越小、PSNR、GMG和LS越大、K值越接近1，圖像越清晰，輪廓越鮮明，圖像質量越好，復原結果越接近退化原始圖像，T值越小，算法效果越好。

3.2 實驗結果對比及分析

在不含噪聲的情況下，本文選取標準圖像庫中的圖像，對原始清晰圖像經過同一模糊尺度和模糊角度的運動模糊，分別使用逆反卷積、維納去卷積、R-L算法和本文的復原方法對計算機仿真運動模糊圖像進行復原，復原結果如圖2所示。

選用主觀評價方法和客觀參數評價對Lena圖像復原效果進行評價，結果如表1所示。

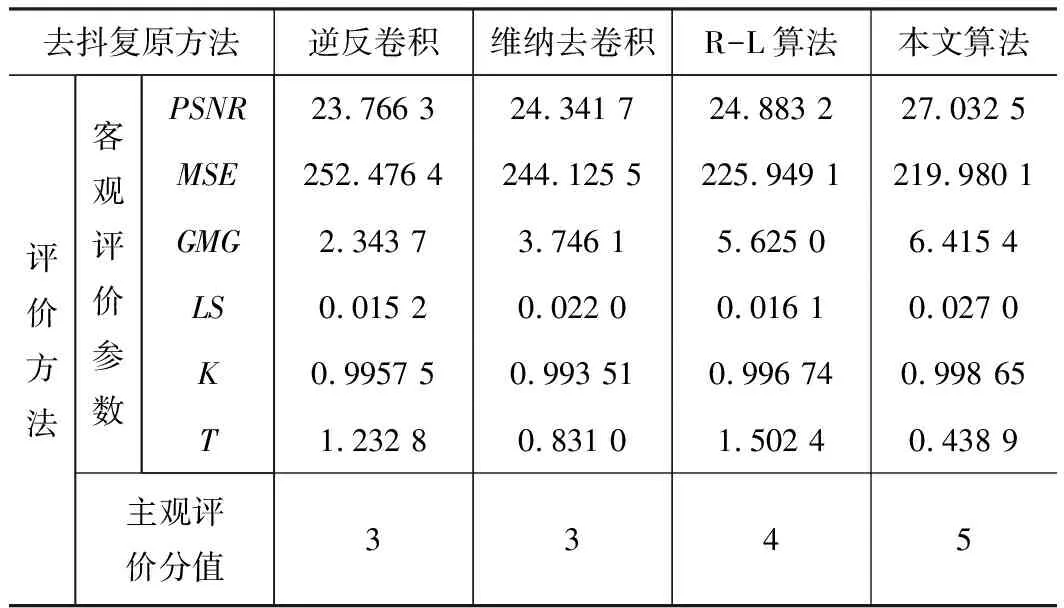
表1 4種圖像復原方法評價參數對比

根據復原結果圖以及復原圖像質量評價結果得到如下結論：

(1)逆反卷積和維納濾波對無噪聲的運動模糊圖像的去抖效果較差，復原后圖像的清晰度較低，輪廓不是很鮮明。

(2)R-L方法對圖像的清晰度和輪廓的復原效果較好，但是圖像的信噪比PSNR不高，而且由于算法的運算量增大，計算時間變慢。

(3)通過客觀和主觀評價的結合，而且客觀參數的增加，使得評價效果更好。本文方法的復原圖像具有較高的PSNR值、較小的MSE值，圖像清晰，輪廓鮮明，且計算時間較小。這種方法可以同時實現多參數客觀評價、抑制振鈴效應和縮短計算時間的多重目標。

4 算法的實際應用效果驗證

4.1 實驗平臺搭建

本文采用自行研發的高精度視覺測量系統實驗平臺來采集圖像數據。實驗平臺如圖3，其主要性能參數如下：圖像采集系統采用CGimagetech相機，相機傳感器尺寸2/3英寸，分辨率1392×1040 pixel；光路系統采用艾菲特 BT-2316遠心鏡頭，采用平行背光源照明。測試條件如下，CPU：Intel Core(TM)i3-2330M@2.20 GHz，內存：4 GB；軟件采用C++編程實現。

4.2 實驗結果分析

啟動數控機床和視覺測量系統，在線采集刀具圖像，采集結果如圖4a所示。由于此處在線采集環境的機床振動和其他隨機振動引起的圖像抖動實際是空間性，但本實驗中所用鏡頭是BT-2316景深鏡頭，所以景深方向的抖動可忽略，即空間問題轉化為平面問題，可用本文去抖動方法復原，復原結果如圖4b所示。

同樣采用4種復原方法對實拍圖像進行復原，并對比分析多參數評價方案對實拍刀具復原圖像的評價如表2所示。

表2 實拍刀具圖像復原方法對比

實驗驗證結果分析：

(1)從圖4可以看出，復原后的刀具圖像輪廓變得明顯，但靠主觀觀察評判并不鮮明。

(2)從表2可以看出，本文方法具有較低的均值方差值和較高的拉普拉斯算子和值，而且圖像復原相關測度k值十分接近1，說明本文方法具有較好的復原效果。

5 結語

(1)自適應L-R算法和金字塔相結合的方法不僅很好的抑制了振鈴效應，還大大縮短了計算時間。

(2)圖像復原相關測度K和響應時間T兩個參數的增加使得圖像質量評價方案更客觀、更完善。

(3)本文方法不僅對圖庫Lena圖像的復原效果佳，實拍刀具圖像的復原效果也較好。

[1]王智峰, 唐延東.基于各向異性非線性擴散的圖像消抖算法[J].儀器儀表學報, 2008, 29(S):553-556.

[2]錢翔, 孔藝穎, 葉大田.甲皺微循環顯微圖像去抖動方法的研究[J].北京生物醫學工程, 2011, 30(4):363-367.

[3]馮澤.基于STM32的圖像采集與去抖動模糊的研究[D].上海：上海師范大學, 2015.

[4]周同同.基于相機抖動的模糊圖像的盲復原實現[D].南京：南京理工大學, 2013.

[5]Vorontsov S V, Jefferies S M.A New Approach to blind deconvolution of astronomical images[J].Inverse Problems, 2017,33(5):055004.

[6]Sperl J I, Sprenger T, Tan E T, et al.Model-based denoising in diffusion-weighted imaging using generalized spherical deconvolution.[J].Magnetic Resonance in Medicine, 2017,78(6):2428-2438.

[7]Jiang J, Huang J, Zhang G.An accelerated motion blurred star restoration based on single image[J].IEEE Sensors Journal, 2016,17(5):1306-1315.

[8]王鵬飛.運動模糊圖像復原算法研究[D].重慶：重慶大學, 2013.

[9]胡玲玲.單幅自然圖像復原算法研究[D].杭州：浙江大學, 2013.

[10]Perez V, Chang B J, Stelzer E H.Optimal 2D-SIM reconstruction by two filtering steps with richardson-lucy deconvolution[J].Scientific Reports, 2016, 6:37149.

[11]Bonettini S, Comelio A, Prato M.A new semiblind deconvolution approach for fourier-based image restoration: an application in astronomy[J].Siam Journal on Imaging Sciences, 2013, 6(3):1736-1757.

[12]Yamauchi H, Somha W.A phase shifting multiple filter design methodology for lucy-richardson deconvolution of log-mixtures complex RTN tail distribution[C]// Integrated Circuits and Systems Design.IEEE, 2015:20.

[13]Yamauchi H, Somha W.A filter design for blind deconvolution to decouple unknown RDF/RTN factors from complexly coupled SRAM margin variations[C]//Circuits & Systems.IEEE, 2016:247-250.

[14]Snow N J, Sue P, Borich M R, et al.A reliability assessment of constrained spherical deconvolution-Based diffusion-weighted magnetic resonance imaging in individuals with chronic stroke[J].Journal of Neuroscience Methods, 2016, 257:109-120.

[15]Ingaramo M, York A G, Hoogendoom E, et al.Richardson-lucy deconvolution as a general tool for combining images with complementary strengths[J].Chemphyschem A European Journal of Chemical Physics & Physical Chemistry, 2014, 15(4):794.

[16]Yang H L, Chiao Y H, Huang P H, et al.Blind image deblurring with modified richardson-lucy deconvolution for ringing artifact suppression[M]//Advances in Image and Video Technology.Springer Berlin Heidelberg, 2012:240-251.