例舉用坐標法解反比例函數的中考題

陸漢俊

(江蘇省邗江中學(集團)北區校維揚中學 225100)

反比例函數是初中數學的重要內容之一，更是歷年中考的熱點.近年來各省市中考都有考查反比例函數的難題.由于此類型的題目不僅要考察反比例函數的相關性質，而且常與其它幾何圖形相互結合考察幾何圖形特征，因此考察面較廣又比較復雜.解決此類問題最常用的方法是根據“k”的幾何意義，即模型法.而反比例函數具有兩重性：代數表達式和幾何圖象，因此解決相關問題時，往往可以通過設出點的坐標，建立方程來求解，即坐標法(也稱解析法). 筆者歸納出有以下三種題型可以使用坐標法來解決.

一、面積問題

圖1

解析本題紛繁復雜.雖有面積特征，但與基本三角形轉化聯系不大，所以考慮用坐標法：設點坐標，建方程.

特征1：S△BCE=2S△ADE,E是中點.

而S△BCE=S△ACE,S△ADE=S△BDE，則S△ABC=2S△ABD.

因兩三角形等高(均與CD相等)，

所以，AC=2BD.

特征2：CD=k.

CD=CO+DO=3x0?3x0=k=x0y0，則AC=y0=3.

特征3：AB=2AC.由兩點間的距離公式，

評注通過設點的坐標，結合兩點間的距離公式，可以解決很多關于線段關系問題，包括面積問題.

二、與幾何圖形相結合題

圖2

(1)k的值為____；

(2)在點A運動過程中，當BP平分∠ABC時，點C的坐標是____.

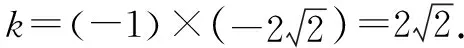
如圖2，過點A作AM⊥x軸于點M,過點C,作CN⊥x軸于點N.

評注大凡涉及到函數的動點問題，應該首先想到設點的坐標，建立方程，可以揭示問題的實質，更易于解決問題.

三、與一次函數相結合題

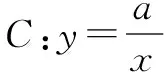
(1)求雙曲線C及直線l2的解析式；

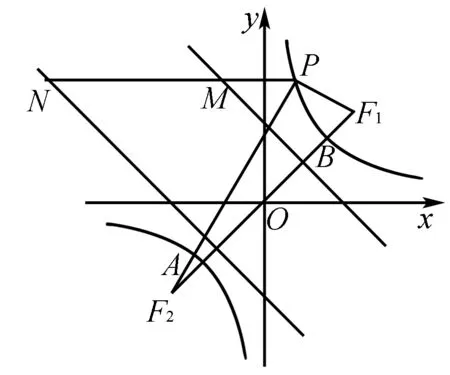
圖3

(2)求證：PF2-PF1=MN=4.

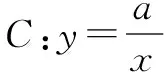
(2)此問至少涉及五個點，其中三個動點.而三個動點P、M、N所在直線垂直于y軸，也就是說縱坐標相等.

綜合分析，設點坐標，建方程.

但PF2-PF1如何表示呢？只要用兩點間距離公式，但心中要有信念：最終未知數必然能抵消掉.

到了這一步，感覺進展下去有點難.怎么辦呢？最終未知數必然能抵消掉.說明這個表達式很有可能是完全平方式.

綜上，PF2-PF1=MN=4.

評注題目若涉及到多個動點問題，則要設主動點的坐標，從而根據動點之間的關系，得出其他從動點的坐標，問題就會迎刃而解.

從以上三例可以看出，抓住反比例函數的雙重性，只要能設出點的坐標，通過列方程或關系式，很多反比例函數難題就會比較容易地得到解決.

參考文獻：

[1]許磊.“反比例函數的圖象與性質”教學設計[J].中國數學教育，2011(1-2)：32-34.

[2]楊晨光.“反比例函數的圖象與性質”聽課思考[J].中國數學教育，2012(6)：23-24.