基于小波變換的采樣問題研究

王銀花 孫 濤

（銅陵學院電氣工程學院 安徽銅陵 244000）

香農采樣定理的內容表述為：一個頻譜有限的信號，當對其用采樣頻率大于信號最高頻率的2倍進行采樣得到樣本數據，則原來的模擬信號可以從樣本數據中完全重建。原始模擬信號的帶寬決定采樣間隔大小，當采樣間隔大小滿足香農采樣定理時，采樣得到的序列不丟失原始模擬信號的全部信息。在通信領域中，由于任何通信設備都有其截止頻率，因此要求原始信號是頻譜有限信號的條件是適合通信系統的實際情況的。但是在其他很多領域如電磁場、地球物理學等，由于所涉及到的信號函數很多是緊支集的，且信號函數本身或者其導數不連續，其傅里葉變換得到的頻域函數的頻譜不可能是有限的，因此香農采樣定理不再能適用。

小波分析是20世紀80年代中后期發展起來的，它是結合泛函分析、應用數學、逼近論、調和分析、廣義函數論等數學知識的結晶。作為一種全新的分析信號的工具，克服了傅里葉分析的只是反映信號的整體特征，而非局部特征的不足，又克服了Gabor提出的窗口傅里葉變換中時—頻窗寬度固定，無法隨意更改窗結構的不足。目前，小波分析在圖像處理、模式識別、數值分析、地震數據勘探和大氣科學等眾多非線性領域越來越發揮出創造性的作用，其潛在的應用領域極其廣泛。

無線電通信是20世紀90年代初發展起來的。由天線感應的射頻模擬信號盡可能直接進行數字化，將其轉化為適合信號處理器或者計算機處理的數據形式，然后可以通過算法來實現各種功能，這樣的做法使數據流具有更好的適應性和可擴展性[1]。因此完成模擬信號的數字化就是極其重要的。信號可以通過采樣方式把模擬信號轉化為離散數值，再通過重構公式和離散點的組合表示出原始信號，香農等人在提出時域采樣定理后，后繼發展了頻域信號的采樣定理，多維信號的采樣定理，廣義平穩信號的采樣定理以及非均勻采樣定理。本文是在非均勻采樣定理的思想下，利用小波變換理論，建立新的基于小波分析的采樣定理，它可以滿足不同領域的各種實際問題的需要。體現出小波分析這一新型工具用于采樣定理的優越性。

一、采樣理論

（一）時域采樣定理。計算機處理信號需要將模擬信號轉換成數字信號，其第一步就是采樣。將連續信號采樣成離散信號，再經過量化，編碼等處理成數字信號。以此得到的數字信號可以通過衛星通道、微波干線、電纜、光纖等數字線路傳輸。

教材中對于滿足頻帶范圍有限的這一限定條件的信號，令其最高頻率為fm，用理想單位沖激響應串δ(t-nT)與模擬信號f(t)相乘，得到離散信號fs(t)，其頻譜結構是原模擬信號的頻譜沿頻率軸，以采樣角頻率ωs為周期的延拓函數[2]。滿足奈奎斯特采樣頻率即（Fs≥2fm(Fs=1/T)）時，用低通濾波器從采樣信號中能不失真的提取原信號。

利用傅里葉反變換求出時域插值公式。即：

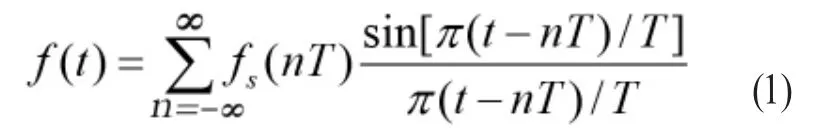
由插值公式與采樣離散點線性組合重構出原始信號。

（1）式右邊用 S△f(t)表示，即：

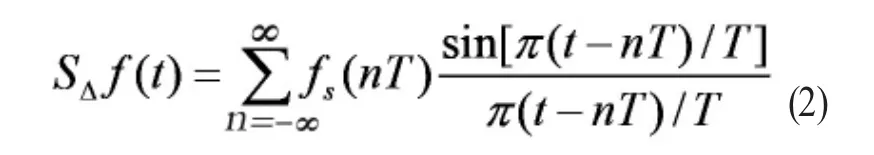
當香農采樣定理的限定條件不滿足時，對于任意取樣間隔，式（1）是不能成立的。即S△f(t)與f(t)會有較大偏差。

采樣問題研究以下兩個問題，第一，用什么樣的采樣方式可以使信號無損失。第二，插值函數的選取并用線性組合無失真的還原出原始模擬信號。

（二）非均勻采樣定理。香農等人曾經指出:當帶限信號f(t)在(-T,T)外，其采樣值準確為零時，則f(t)可以僅由2BT個采樣值來重構，B指的是帶寬。同時，這2BT個采樣值不必是等間隔的采樣值[3]。

非均勻采樣定理可表述為：設f(t)為一帶限信號，其最高頻率為w,則f(t)可以由其某一組在周期非均勻采樣點t=τpm=tp+(mN/2w)，p=1,2......N，m=...-1,0,1...上的采樣值唯一確定。其重構公式為：

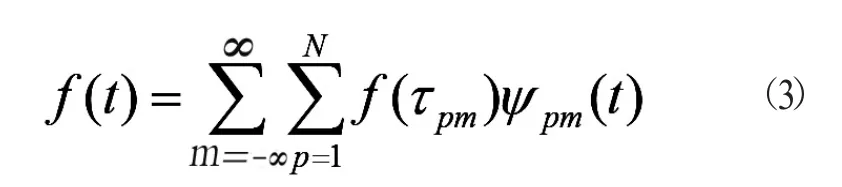
式中

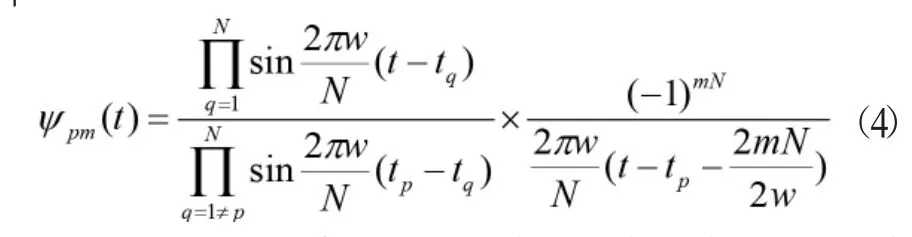
正是基于非均勻采樣的思想，本文研究討論基于小波變換的非均勻采樣定理特性。

二、小波變換與采樣

小波分析是克服傅里葉分析缺陷的一種新型研究信號的工具，傅里葉變換的基函數不是屬于平方可積的信號空間即，而小波函數滿足[4]。令小波函數的傅里葉變換為ψ(ω)，若其滿足條件：

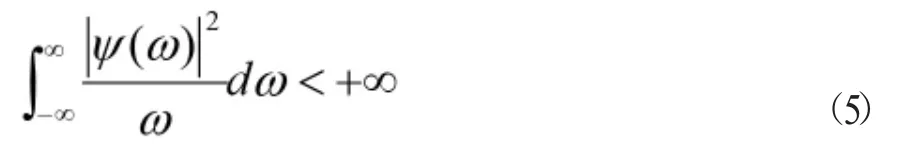
則稱ψ(t)是一個小波母函數。小波函數具有衰減性和正負交替的波動性。由小波母函數經過尺度變換和位移變換可以得到小波基函數。圖1所示就是一種小波基函數。

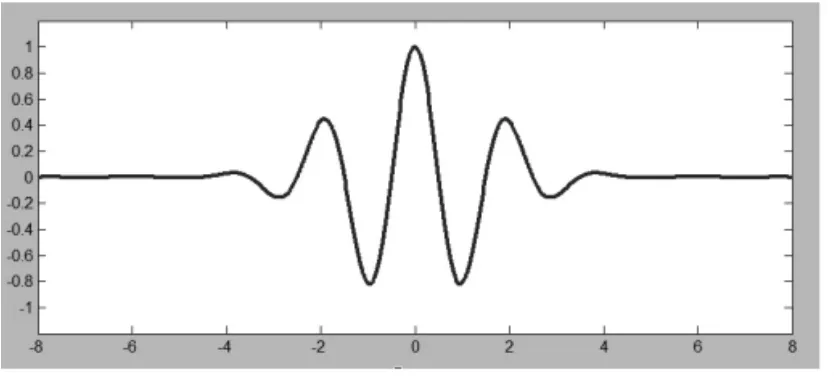
圖1 小波基函數

連續小波基函數的數學公式可表示為：

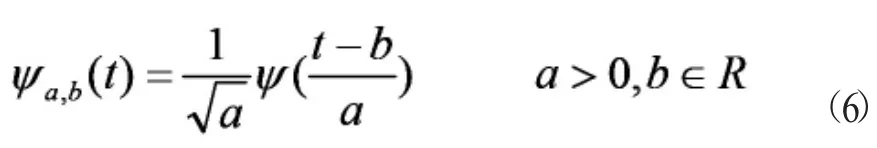
式（6）中為尺度參數，b為位移參數。

信號f(t)的連續小波變換的定義式為：

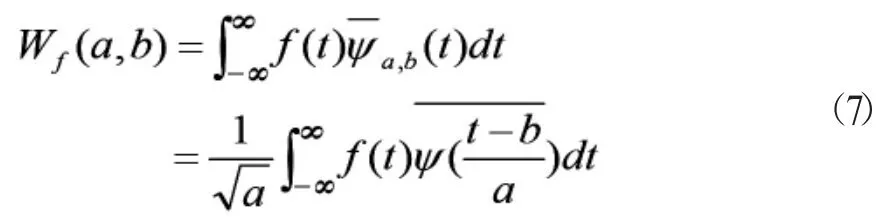
可見小波變換將一維的信號變換成依賴于參數的二維分析，故小波變換實際上是一種升維分析。任何變換必須有其逆變換才有意義。小波變換的逆變換是存在的。根據小波變換系數可以精確的恢復原信號。小波逆變換公式為：

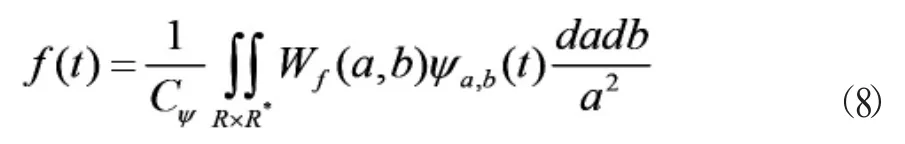
式（8）說明對連續小波變換系數與小波基函數的乘積再做二重積可確定信號f(t)的重構。

信號f(t)的連續小波變換系數信息是冗余的，在許多情況下，需要考慮數據壓縮和存儲計算，如圖像數據壓縮、語音數據壓縮、數值計算等領域。希望在不丟失原始信號f(t)的情況下，盡可能地減小小波變換系數的冗余度。非正交離散小波變換能夠滿足這方面的要求。

式（7）中，當ψ(t)是正交小波時，應滿足以下條件：

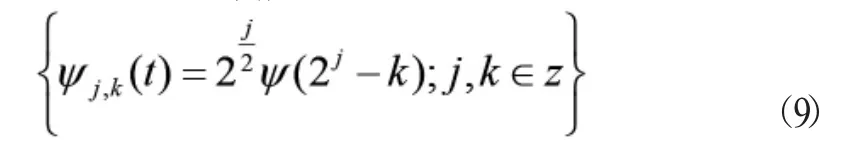
按照尺度參數=2-j，位移參數b=2-jk將小波離散化處理，降低了連續小波變換的冗余性。

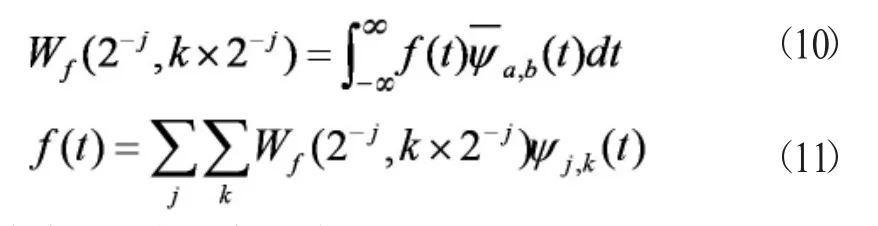
將式（10）帶入式（7）得

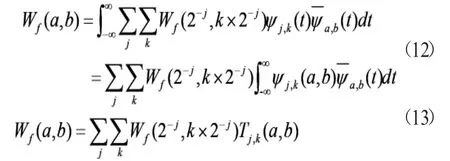
其中。

式（13）就是小波采樣定理。對于任意f(t)∈L2(R)，連續小波變換系數Wf(a,b)把尺度參數和位移參數離散化后的Wf(2-j,k×2-j)與插值基函數Tj,k(a,b)相乘，二重求和就可以重構原始信號。

三、Harr小波

以Harr小波為例，它是最早用到的，最簡單的具有緊支集的正交小波。

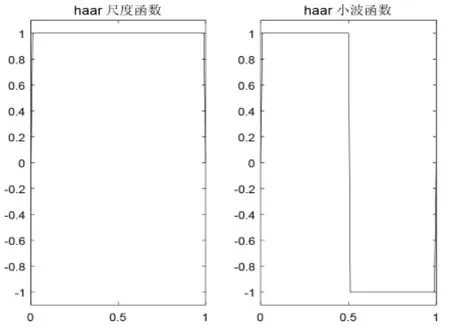
圖2 Harr尺度函數和Har小波函數

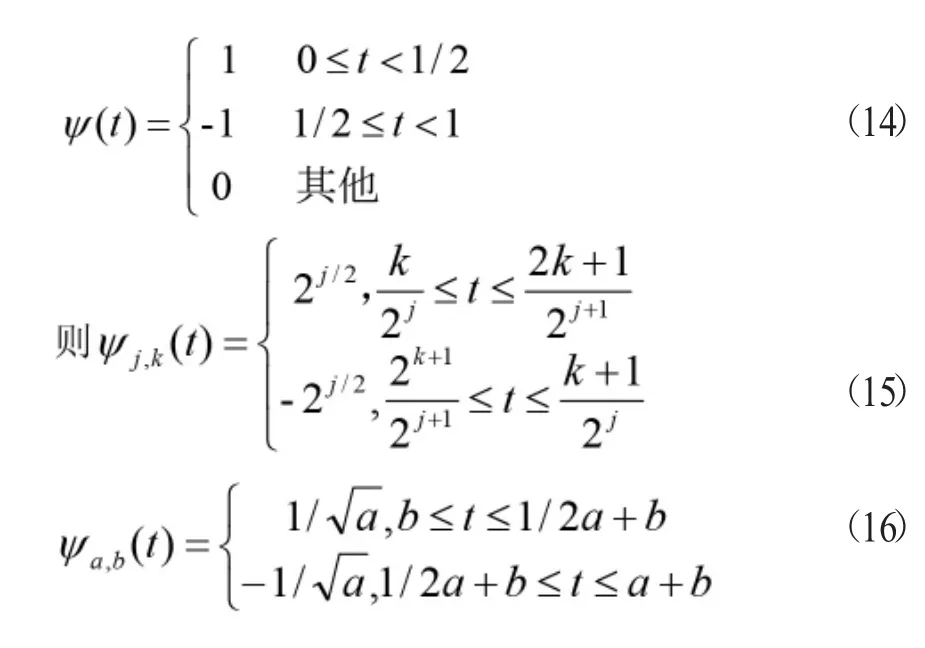
由式（13）得。

下面分情況討論，由此得出了中的表達式和圖像。

情況①：當，即

則由式（16）得

同理，情況②：當

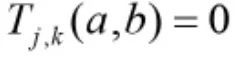
情況③：當

利用MATLAB畫出情況③的Tj,k(a,b)圖像如圖3。

圖3 情況③的圖像

情況④：當

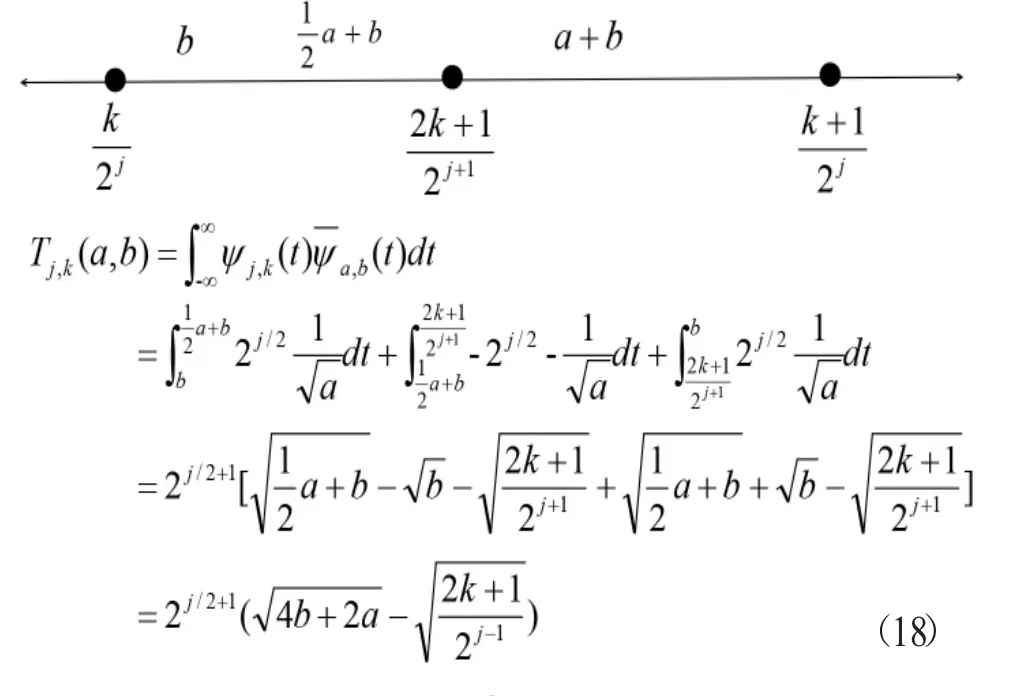
利用MATLAB畫出情況④的Tj,k(a,b)圖像如圖4。

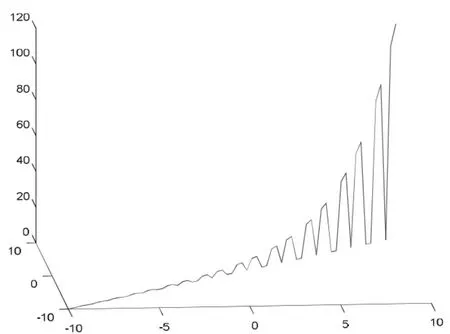
圖4 情況④的圖像

四、結束語

隨著科學技術的飛速發展，計算機和數字化處理得的實際運用越來越多，采樣理論已經成為現代信號處理領域的重要基礎和關鍵技術。經典采樣定理僅對帶限信號成立[5]。實踐中在處理頻域非緊支集和非均勻采樣信號時，香農定理很難保證信號的無失真傳輸，為解決這一問題，廣義采樣理論得到了迅速發展，廣義采樣研究的一個重要方向即是小波采樣理論[6]。本文以Harr小波為基礎，詳細逐步推論出小波采樣定理的優越性。在香農采樣定理當中，單位理想沖激串是等間隔采樣的，而小波采樣定理卻不要求等間隔采樣，而是以2-j整數倍為采樣間隔。同時在香農采樣定理當中，要求原始模擬信號f(t)是頻帶有限的連續信號。而利用小波采樣理論卻只要求信f(t)∈L2(R)，也即。這顯然降低了帶限信號的要求。由此看出小波升維分析的優越性。

[1]王志田.軍用軟件無線電通信技術發展分析[J].中國新通信，2016(24)：23-24.

[2]燕慶明.信號與系統教程（第二版）[M].北京：高等教育出版社，2010：139.

[3]李秋生，也麗華.帶通信號采樣理論中的若干問題研究[J].井岡山大學學報（自然科學版），2017(2)：61-65.

[4]王經民.小波分析[M].陜西：西北農林科技大學出版社，2004：190.

[5]周盼盼,付應雄.一類非帶限信號的采樣定理[J].湖北大學學報（自然科學版），2017(5)：542-545.

[6]張治國,黃建國,劉震.小波采樣的濾波算法研究[J].湖北大學學報（自然科學版）電子科技大學學報，2010(6)：900-905.

[責任編輯 鄭麗娟]