淺析高中數學教學中如何培養學生的創新思維能力

◎霍峰

對一個人來說，具備創新思維的能力是非常重要的。在高中階段，數學屬于非常重要的一門課程，培養學生的創新思維對教師來說具有非常重要的現實意義。高中數學知識比較抽象難懂，在教學過程中，教師要注意引導學生積極動腦，讓學生在不斷解決數學問題的過程中理解數學知識的本質。

一、教學中存在的問題

1.缺少互動交流 在傳統的高中數學教學過程中，老師與學生之間缺少互動交流，學生很難在課堂上發揮作用，學生只是在被動地接受一些理論知識，而絲毫對數學學習產生不了興趣，這就導致了教學有名無實，效率低下。尤其是在高中數學這樣理論性特別強的學科，如果只是老師在上面講解，而調動不了學生的學習積極性，那么就只能是學生的學習效率不高，不能達到一種理想的教學效果。

2.教學模式單一 由于受到傳統教學模式的影響，在高中數學教學過程中出現了教學模式單一的現象。就是老師在教學過程中用單一的教學模式進行教學，老師一心只想將所有知識傳授給學生，卻忽視了學生的承受能力。老師在教導學生的時候，往往在單一地強調考試分數的重要性，卻忽視了對學生各方面能力的培養，學生的各個方面的能力都得不到提高和發展。

二、培養創新思維能力方式

1.培養學生的質疑能力 學生的質疑來自于學生對問題的思考，高中學生對數學知識的獲得主要表現在記憶和解題上，缺乏對知識間的聯系和分析，被動接受的多、主動反思的少。如在講數學歸納法時，為了說明完全歸納法和不完全歸納法的區別，特別設計了兩個問題：（1）你們班1號同學是戴眼鏡，2號同學戴眼鏡，3號同學戴眼鏡，結論是：全班同都戴眼鏡（哄堂大笑）；（2）全班45位同學，給每位同學量身高，最小1.45m，最大1.83m，結論是：全體同學身高都在lm以上。這樣的設計，使許多同學在思考為什么第一個問題得到的結論是錯誤的，第二個問題得到的結論是正確的。同時，使學生理解了兩種歸納法的區別。

2.師生密切溝通 在高中數學的教學過程中，教師要注重和學生的有效溝通，對學生數學思維能力進行有效提升，與教師的努力也是不可分害分割的。那么教師要想解決傳統的數學課堂教學中的灌輸式教學方式，就需要加強和學生的溝通，充分了解學生的真實情況，掌握學生不理解的知識點或問題，并根據學生的實際情況制定有效的應對方案，幫助學生開展更有效的指導和幫助，滿足學生的心理，讓學生在不斷探索的過程中積極尋求答案。在師生溝通的過程中，教師還需要關注學生的心理變化，以便在發現問題的時候及時解決，為學生數學思維能力的提升和完善提供更有效的幫助。

3.創新思維品質的培養 傳統的數學教學側重于傳授，使學生在學習過程中只能被動地接受書本知識，這種教學活動極大地限制了學生創新思維的發展，也從一定程度上扼殺了學生的想象力和創造力。前蘇聯著名數學教育家斯托利亞爾指出：數學教學應按數學思維的規律進行。因此，在數學教學中，應采用多種手段通過對基礎知識的認識，熟練掌握和成功運用，通過對圖形的觀察分析，對數學符號的應用與思考，使學生在邏輯理解，抽象概括，變化聯想等方面，得到數學思維的訓練，從而培養學生思維的敏捷性，變通性，直覺性和獨創性等創新思維的優良品質。以余弦定理為教學案例，設計時為了充分發揮學生的自主創新意識，則以問題為中心，解決問題為主線，讓學生通過不斷地探究，達到深刻領會概念、自覺運用知識、完善知識結構的教學目標。

問題1：（如圖1）在直角三角形中，∠A=90o，a2=？

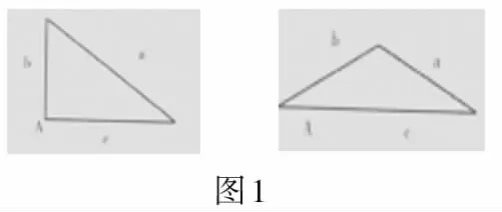
問題2：當∠A≠90o時，a2與b2+c2的大小關系如何？（CAI演示）

問題3：如∠A＞90o（或∠A＜90o），a2與 b2+c2的差值是什么？如何找出這個差值？（可用b，c及∠A的式子表示）

問題4：推導方法除添垂線外，還可用哪些簡捷方法？（如坐標法等）

問題5：如何建立坐標系，可使推導過程簡潔一些？

問題6：此結論與勾股定理的關系如何？

問題7：（開放性）應用此結論（余弦定理）可解決哪幾類解三角形中的問題？

問題8：（開放性）請你編擬幾個簡單的計算問題

以上的問題系列設計，突破了傳統的教學模式，激勵了學生的創新思維。

三、結束語

綜上所述，在進行數學教學的過程中，想要使學生的創新思維能力得到培養，是非常復雜的事情。而想要使學生的創新思維能力得到培養，老師就應當在日常的教學過程中加強與學生的交流，按照實際情況進行數學教學。將培養學生的創新思維能力作為主要教學任務來抓，達到培養學生創新思維能力的目的。

［1］楊開昌.高中數學教學創新能力的研究.新課程2015（08）.

［2］劉勝廣.高中數學教學創新能力的研究.吉林教育201（13）.