淺析對稱思維法在高中物理解題中的應用

□盧翔遠

對稱現象普遍存在于物理現象和規律中，借助對稱思想解題，就是建立更加有效且簡便的方式進行物理推導，從而減少復雜的驗算過程。

一、電學試題中應用對稱思維法

1.電路對稱。在有關電路題的解答過程中，教師要引導學生有效尋找對稱點，并且判定相應的關系，從而有效分析題目。

例題1：圖1為相同材料金屬棒構成的四面體，若將小件金屬棒的實際電阻設定為r，求解從點A到點B之間的電阻。

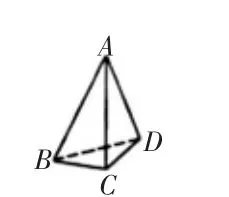
圖1

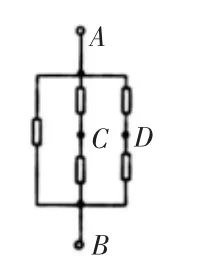
圖2

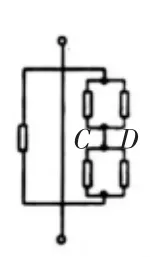
圖3

例題解析：結合題目中的相關信息，教師可以引導學生將立體圖形轉化為平面圖形，從而更便于尋找對稱結構。將圖1轉化為圖2，正是由于C點和D點本身就是對稱點，因此，兩者形成了等電勢關系，為等勢點。通過相關知識可以了解到，等勢點之間沒有電流通過，將兩者斷開即可，保證等勢點得以重合（如圖3）。因此，就得出最終的結論，電阻是r/2。

2.電荷分布對稱。在電學考察項目中，電荷問題成了近幾年高考中較為常見的考點。

例題2：均勻帶電的球殼，在球體的外部空間會產生電場，其產生的等效電荷主要集中在球心位置，其產生的電場為圖4。并且，在半球面AB上是均勻分布的正電荷，總體電荷量為Q，球面半徑為R，且CD是通過半球頂部和中心O相連的軸線，若是在軸線上標定點M和點N，則相關距離滿足OM=ON=2R，結合已知條件，若是M點的場強為E，求解N的場強。

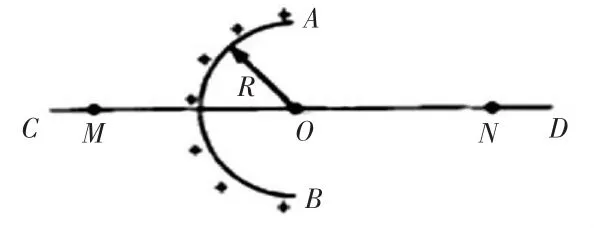
圖4

例題解析：這是較為常見的場強分布判定問題，學生要在仔細閱讀題目中已知條件的基礎上，有效整合相關數據。在半球面AB之間分布的是正電荷，其產生的電場設定為K，正電荷處于均勻分布狀態，另一側則為充滿負電荷的球面，形成電場的矢量合為E=這就說明帶有負電荷的另一側球面在M位置的實際電場參數和AB電場中N電的大小相等。

通過解析不難發現，在電荷分析和討論的題目中，對稱性較為關鍵，要結合已有知識和對稱一側的數據進行分析，并且建構有效的對稱圖形，簡化計算過程，有效提出合理的假設和變換問題，一定程度上簡化問題的難度。

二、力學中應用對稱思維法

1.運動過程對稱問題。在力學應用體系中，對稱現象也較為常見，尤其是對運動過程中的時間進行對稱分析，能建立兩個不同的運動系，從而判定運動過程中存在的問題。

例題3：若是一個人在距離地面H的高度位置，以初速度υ0同時拋出小球A和小球B，其中，小球A是向上豎直拋出，而小球B則是向下豎直拋出，結合實際運行軌跡可判定，兩者的落地時間差為△t，求解初始速度υ0。

例題解析：在對不同情況進行分析的過程中，要建立兩個運動系統。首先是小球A，由于是豎直向上拋出，因此，在其回落到拋出點時，運動狀態呈現出對稱形式，尤其是速度，那么，小球A向下的速度也是υ0，這就使得小球A在拋出點以下的運動和小球B的運動屬于一種運動形式，且落地時間也是相同的。因此，得出最終的結論，△t其實就是小球A向上的運動時間，按照公式計算得出

通過解析不難發現，在對運動學中對稱問題進行思考的過程中，教師要引導學生對整個過程和最終形成的狀態予以判定，從而建構有效的運動系。

2.簡諧運動對稱。簡諧運動是最簡單、最基本的機械振動。簡諧運動本身就具備對稱性，學生在做相關題目時，要在判斷運動形式后，應用運動的特性進行分析。

例題4：圖5中質量為m1的框架上懸掛了兩個物體，質量分別為m2和m3，且m2＞m3。在初始狀態，三者均呈現靜止態，然后剪斷兩個物體之間的連線，拿走質量為m3的物體，在物體m2向上運動后，達到最高點，此時，彈簧會對框架結構產生作用，試問大小為多少？而框架此時對地面產生了多少壓力？

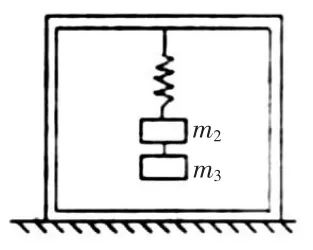
圖5

例題解析：結合圖中的相關已知條件進行分析，在剪斷繩子后，整個系統中m2會做豎直向上的運動，為簡諧運動形式，就為整個題目的解答奠定了對稱分析的基礎。在剪斷的瞬間，質量為m2的物體會直接以加速度豎直向上，且加速度要大于重力加速度。在質量為m2的物體上升到最高點后，結合簡諧運動的對稱特性，就能對物體向下加速度大小進行判定，和上升加速度一致，為。除此之外，在該點還能保證狀態和最低點相對稱，也就能有效分析并且描述簡諧運動的矢量參數，存在大小相等方向相反的特性，若是彈簧被拉伸，若設彈力為F，就說明m2g-F=m2a'。綜上所述，能對最終得出的結論進行判定，F是質量為m2和m3物體重力的差值，彈簧框架的作用力就是質量為m1物體的重力和F的和，也就是F壓=（m1+m2-m3） g。

3.碰撞運動對稱。在對運動進行分析的過程中，也要結合公式對具體問題進行具體解讀，尤其是碰撞問題，要對碰撞前、碰撞后等運動結構展開系統化分析，才能有效判定相關參數之間的關系。

例題5：圖6中沿著水平方向拋出小球，拋出點和地面之間高度差為h，距離墻壁的水平距離為s，若是小球和墻壁發生彈性碰撞，則能直接落在水平地面位置，落地點和墻壁之間的距離記為2s，求解小球的實際初速度υ0。

圖6

例題解析：小球和墻壁出現了彈性碰撞，此時小球會以初速度υ0垂直于墻壁向上運動，形成彈回的趨勢和運動軌跡，而在碰撞前后小球得到實際速率均相等。由于平行墻壁的方向較為光滑，導致速率也不會發生變化，另外，碰撞結束后小球的軌跡和沒有墻阻擋的小球呈現出對稱軌跡，結合小球進行的平拋運動機理，對其進行分析，得出

總而言之，教師要培養學生的物理素養，建立健全有效的教學框架體系，引導學生解答疑難問題，從而提高物理解題水平，優化教學效果。

參考文獻：

[1]高耀東.例談對稱法在高中物理解題中的應用[J].理科考試研究(高中版),2013,(10):41-42.

[2]王家山.對稱法在中學物理解題中的應用[J].物理教師,2014,(10):64-66.

[3]施劍峰.關注物理過程中的“偽對稱”[J].中學物理（高中版）,2013,(9):77.