城市環境下GPS/BDS融合偽距定位性能分析

王 翀,王振杰

(中國石油大學(華東)，山東 青島 266580)

GPS能為全球用戶提供高精度的導航定位服務，但在觀測條件較差時，其可見衛星數、定位精度和可用性都有所下降[1-2]。隨著全球導航定位服務需求量的增大，保障定位連續性和可靠性成為首要任務。理想觀測條件下，GPS差分定位誤差的標準差在0.3 m左右[3]。然而，在高樓密集的城市環境下，受衛星信號遮擋和多路徑效應的影響，可見衛星數少、衛星星座結構不理想，導致GPS定位連續性下降[4-5]。多路徑效應和非視距信號誤差對定位精度的影響可達100 m[6]，無法滿足行人和車輛導航定位的精度要求，限制了GPS的應用領域。近年來，多模多頻的導航衛星系統使得用戶在復雜的觀測環境下也能夠獲得較多的觀測值和較好的衛星空間幾何結構[7]，從而有助于改善城市環境下的定位精度。

中國的北斗衛星導航系統BDS(Beidou Navigation System)集導航定位、授時、用戶監測、短報文通信于一體，技術體制上有創新[8]。BDS已于2012年開始向亞太地區提供導航、定位和授時服務，目前已有23顆在軌衛星，2020年左右將建成覆蓋全球的衛星導航系統。隨著BDS的快速發展，融合BDS的多模GNSS數據統一處理已經成為衛星導航定位領域的主要發展趨勢之一，多余觀測量的增加能夠提高單點定位和差分定位的成功率，大幅度提高定位精度，增強單一GPS的定位可靠性和穩定性[9-12]。

本文將研究GPS/BDS時空統一的轉換模型及偽距定位的數學模型，基于自主編寫的GNSS數據處理程序解算城市環境實測數據，并對城市環境下GPS/BDS融合定位與單系統定位的連續性和可靠性進行比較分析。

1 GPS/BDS時空系統的統一

時間系統和坐標系統是導航定位的參考基準，任何形式的導航定位都是在一定的時間和坐標框架內進行[13-14]。北斗采用的是CGCS2000國家大地坐標系統和北斗時間系統；GPS采用的是WGS-84坐標系統和GPS時間系統[15-16]。多系統融合解算前需將時間系統和坐標系統進行統一。

1.1 時間系統統一

GPS時間系統屬于原子時系統，時間起算原點為1980-01-06 UTC 0時0分0秒，秒長與原子時相同。GPST不存在跳秒，與UTC的關系為

GPST=UTC+1 s×n.

(1)

式中n是UTC跳秒次數。

BDS時間系統同樣屬于原子時系統，時間起算原點為2006-01-01 UTC 0時0分0秒，秒長與原子時相同。BDT同樣不存在跳秒，由于UTC閏秒，從1980-01-06—2006-01-01，GPST與UTC存在14 s的系統偏差，因此，BDT和GPST之間相差14 s，兩者的關系為

BDT=GPST-14 s.

(2)

在GNSS融合定位中，所有衛星的觀測數據都記錄在一個觀測文件中，時間系統采用GPST。

1.2 坐標系統統一

WGS-84坐標系統與CGCS2000國家大地坐標系在原點、尺度等方面都是相同的，參考橢球也很相近。在4個橢球常數a，GM，f，ω中，只有扁率f有微小差異。在坐標系的實現精度范圍內，可以認為CGCS2000與WGS-84是一致的[17]。WGS-84、CGCS2000坐標系統參考橢球定義的大地參數見表1。

表1 WGS-84，CGCS2000坐標系統橢球參數

2 GPS/BDS偽距定位數學模型

2.1 單點定位模型

以GPS為例，偽距測量的觀測方程為

(3)

(4)

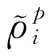
將GPS,BDS雙系統觀測方程在測站近似位置(X0,Y0,Z0)處泰勒展開至一次項，得到誤差方程為

(5)

(6)

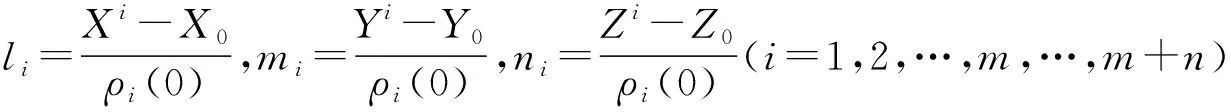
(7)

本文中電離層延遲改正使用Klobuchar模型，對流層延遲改正使用HopField模型，觀測值采用衛星高度角定權方式，為了分析單系統與多系統模式的定位差異，GPS與BDS系統間觀測值等權處理。

2.2 差分定位模型

設接收機i，j在同一觀測時刻對衛星p進行觀測，可得偽距觀測方程：

(8)

將上式中兩式相減可得：

(9)

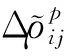
類似式(9)可寫出接收機i，j同一時刻觀測衛星q的單差觀測方程

(10)

將式(9)與式(10)相減，在衛星p與衛星q的單差觀測方程基礎上求二次差為

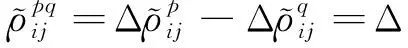
(11)

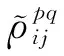
(12)

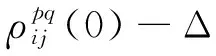
(13)

由最小二乘估計可以求解未知參數陣中的3個坐標差參數。

3 實測數據分析

本文數據源自香港地區車載實測數據，數據采集采用Trimble R10接收機。香港地區具有信號遮擋強、多路徑效應明顯等典型城市環境特點，數據概況見表2。數據處理基于Visual C+平臺編寫GNSS多系統融合偽距定位程序，對實測數據分別以GPS單系統、BDS單系統、GPS/BDS雙系統融合3種模式進行單點、差分定位解算，基準站為HKST站，衛星截止高度角為10°。實驗路線見圖1。

表2 實測數據概況

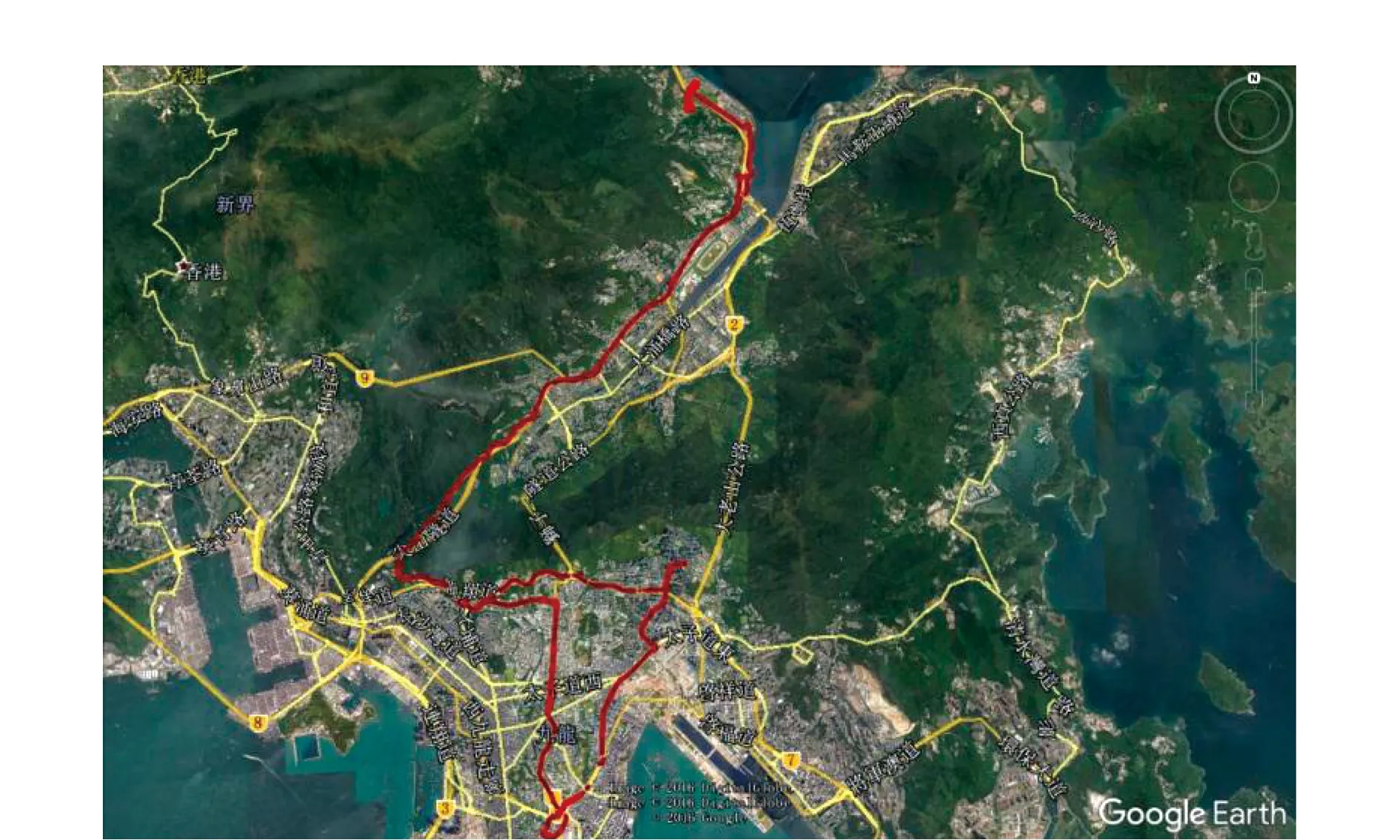
圖1 實驗路線

3.1 可見衛星數和PDOP值

根據原始數據得到觀測時段內GPS，BDS和雙系統融合3種模式的可見衛星數信息，如圖2(COM代表雙系統融合模式)，雙系統融合可見衛星數相比單系統有顯著增加，受城市復雜觀測環境的影響，呈現出一定的波動性。圖3給出空間位置精度因子PDOP值，雙系統融合的PDOP值均小于單系統，可見PDOP值和衛星數呈反相關關系，PDOP值越小，對應的可見衛星數越多，星座結構越合理。因此，多系統較單系統有著更合理的衛星分布和更高的定位精度。觀測時段內可見衛星數、PDOP值的平均值如表3所示。3種模式PDOP值均值均大于3，可見在城市復雜環境下定位精度低于開闊環境。

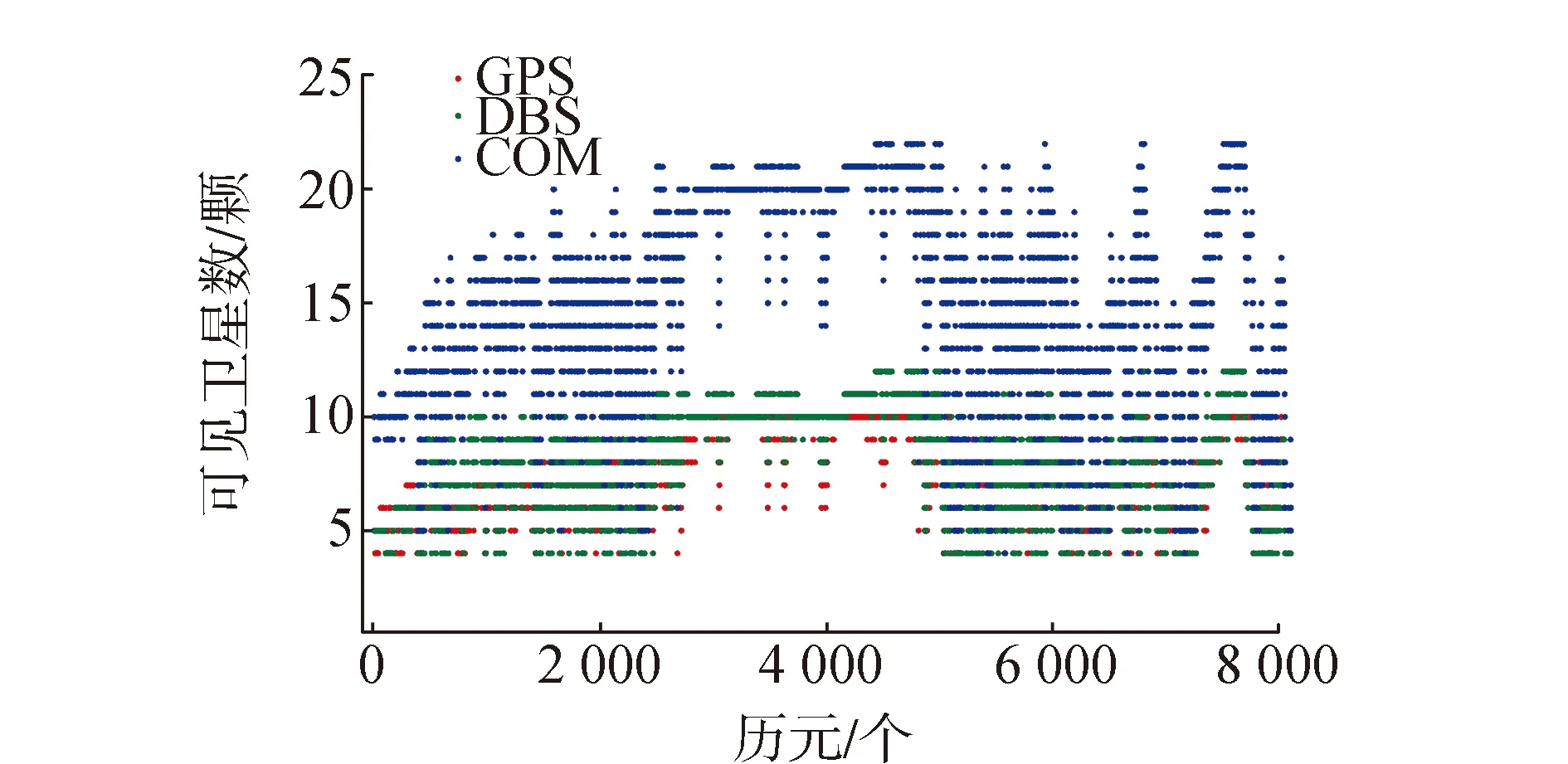
圖2 GPS/BDS/系統融合可見衛星數

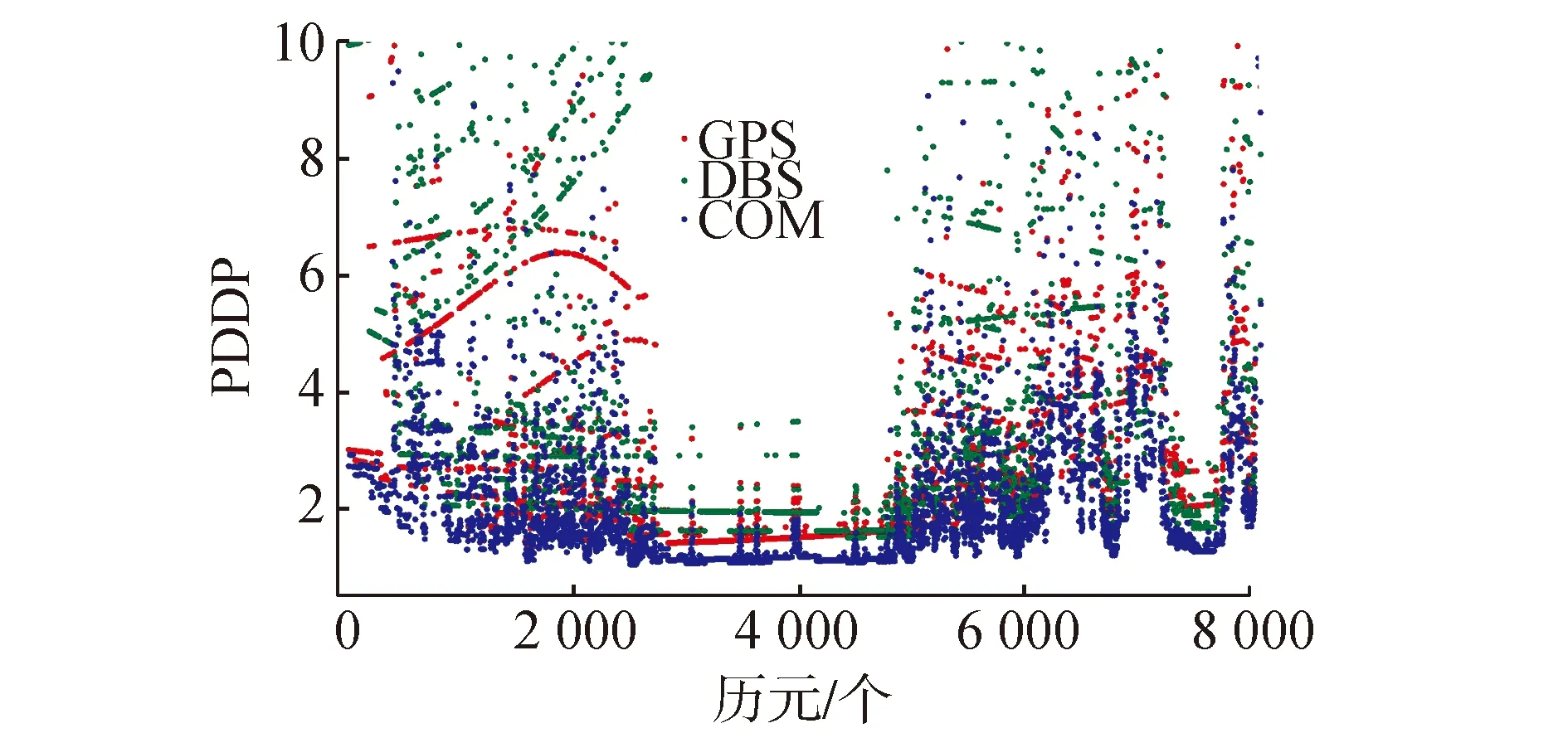
圖3 GPS/BDS/系統融合PDOP值

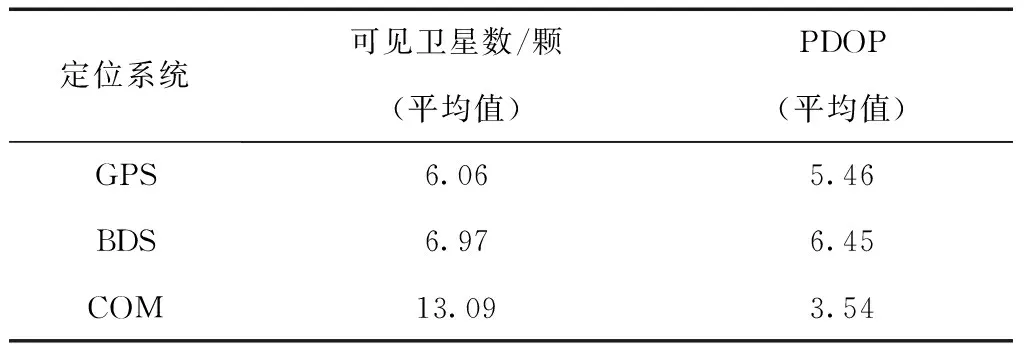
定位系統可見衛星數/顆PDOP(平均值)(平均值)GPS6.065.46BDS6.976.45COM13.093.54

3.2 定位連續性和可靠性

經計算統計，觀測時段內3種模式單點、差分定位的連續性指標如表4所示，本文統計的定位連續性即能夠解得定位結果的歷元數占全部觀測歷元的百分比。可見，GPS定位連續性高于BDS，兩者均小于雙系統融合模式。造成此現象的原因為：雖然整體上BDS可見衛星數多于GPS，但BDS星座結構比GPS略差，在城市復雜環境中無法保證足夠可見衛星數，導致BDS定位連續性低于GPS；差分定位連續性低于單點定位的原因為：選取單基準站，無法保證同步觀測流動站所有可視衛星，導致公共衛星少于流動站可見衛星。受城市復雜觀測環境的影響，雙系統融合模式定位連續性也無法達到100%。

單系統和雙系統組合模式單點、差分定位的RMS值如圖4、圖5，其中3種模式在第2500—5000歷元內的RMS值均較穩定，在其它歷元內波動明顯，結合圖2、圖3可以明顯看出在可見衛星數多，PDOP值較小的城市開闊環境中，定位可靠性較高，而在城市復雜環境中， 定位精度存在明顯波動， 導致定位可靠性大幅度降低。結合表5可以看出雙系統融合定位精度相比于單系統有小幅度提高，主要是由于多系統融合增加了空間可見衛星數，改善衛星空間幾何結構，降低PDOP值。但城市環境中多路徑效應等誤差明顯，僅通過多系統融合無法明顯提高定位精度。

表4 定位連續性統計

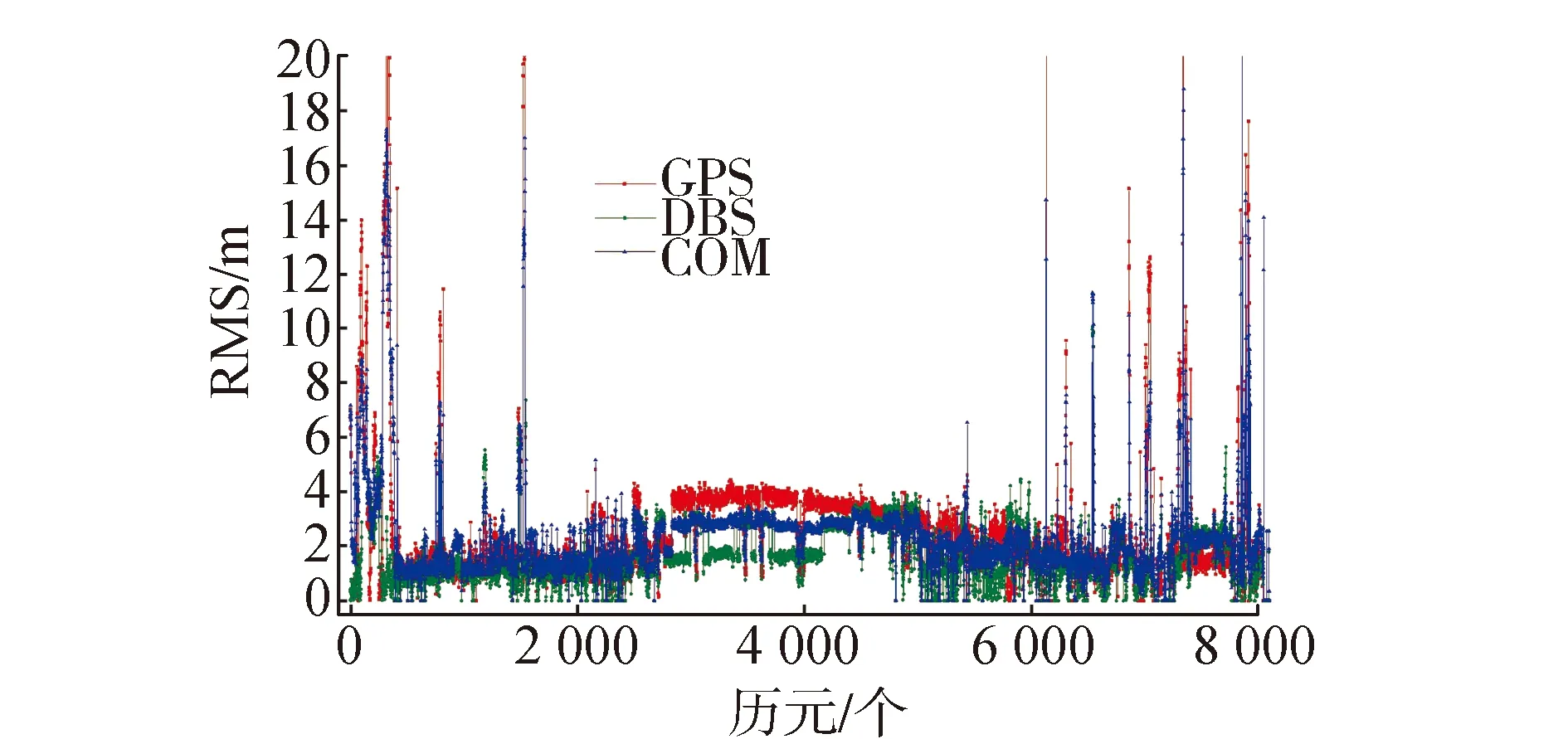
圖4 GPS/BDS/系統融合單點定位RMS

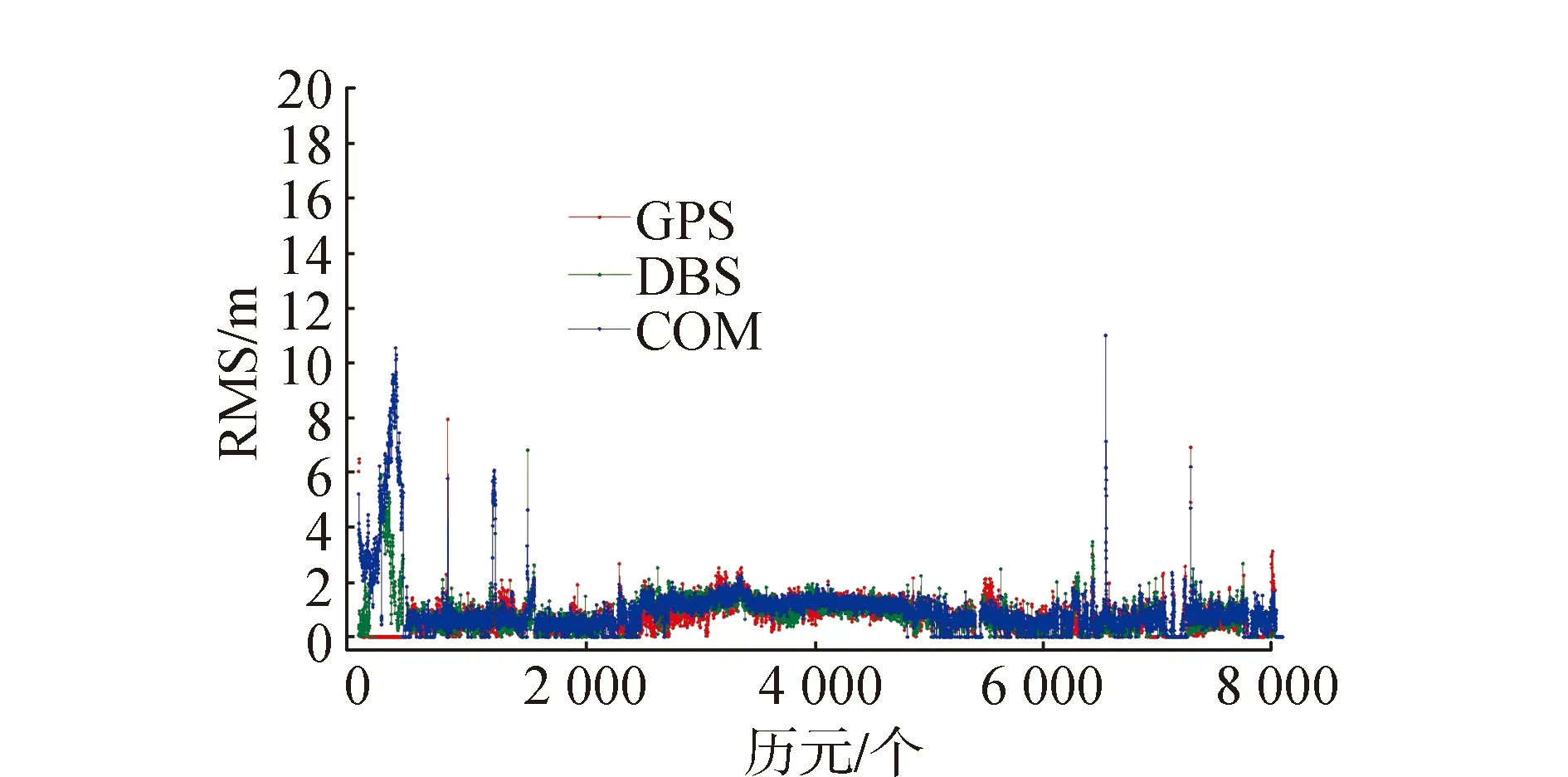
圖5 GPS/BDS/系統融合差分定位RMS

定位方式單點定位差分定位衛星系統GPSBDSCOMGPSBDSCOMRMS均值/m2.681.982.421.231.361.01RMS最大值/m28.3310.0624.057.936.819.65

4 結束語

觀測環境的優劣對衛星定位結果有著顯著影響。本文利用香港地區城市環境實測數據對BDS/GPS雙系統融合偽距定位結果與GPS、BDS單系統在可見衛星數、PDOP值、定位連續性、可靠性等方面進行比較分析，得到以下結論：

1)城市環境建筑物數量多、密度大、信號遮擋強、多路徑效應明顯等特點導致定位結果誤差大，定位連續性差、可靠性低。

2)多系統融合增加單一系統的觀測衛星數，改善衛星相對于測站的空間幾何分布，有效減小PDOP值，提高系統冗余性。

3)多系統融合明顯改善城市環境下定位的連續性，單點定位連續性提升至97.77%，差分定位連續性提升至92.52%，說明多系統融合定位在城市環境下的優越性。

相比于單系統，多系統融合小幅度提高城市環境定位精度，綜合考慮城市環境中多路徑效應等誤差將進一步提高定位精度。下一步工作將針對城市環境多路徑效應展開研究。

[1] 王澤民,孟泱,伍岳,等. GPS、Galileo及其組合系統導航定位的DOP值分析[J]. 武漢大學學報(信息科學版), 2006, 31(1):9-11.

[2] 唐衛明,徐坤,金蕾,等. 北斗/GPS組合偽距單點定位性能測試和分析[J]. 武漢大學學報(信息科學版), 2015, 40(4):529-533.

[3] REZAEI S, SENGUPTA R. Kalman Filter-Based Integration of DGPS and Vehicle Sensors for Localization[J]. IEEE Transactions on Control Systems Technology, 2007, 15(6):1080-1088.

[4] HSU L T, CHEN F, KAMIJO S. Evaluation of Multi-GNSSs and GPS with 3D Map Methods for Pedestrian Positioning in an Urban Canyon Environment[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2015, E98.A (1):284-293.

[5] YANLEI G, LI-TA H, SHUNSUKE K. Passive Sensor Integration for Vehicle Self-Localization in Urban Traffic Environment[J]. Sensors, 2015, 15(12):30199-220.

[6] MACGOUGAN G, LACHAPELLE G, KLUKAS R, et al. Performance analysis of a stand-alone high-sensitivity receiver[J]. GPS Solutions, 2002, 6(3):179-195.

[7] 張麗. GNSS接收機多系統兼容定位算法研究與實現[D]. 北京：北京理工大學, 2014.

[8] 楊元喜. 北斗衛星導航系統的進展、貢獻與挑戰[J]. 測繪學報,2010(1):1-6.

[9] 寧津生,姚宜斌,張小紅. 全球導航衛星系統發展綜述[J]. 導航定位學報, 2013,1(1)：1-6.

[10] 李鶴峰,秘金鐘,黨亞民,等. 基于CORS的多基準站BDS/GPS融合差分網定位性能分析[J]. 大地測量與地球動力學, 2014(6):81-85.

[11] 周萬振,秘金鐘,李得海,等. BDS/GPS/GLONASS融合網格偽距差分定位性能分析[J]. 測繪科學, 2016, (12):5-9.

[12] 李敏. 多模GNSS融合精密定軌理論及其應用研究[D]. 武漢: 武漢大學, 2011.

[13] 高星偉,過靜珺,程鵬飛,等. 基于時空系統統一的北斗與GPS融合定位[J]. 測繪學報, 2012, 41(5):743-748.

[14] 李鶴峰,黨亞民,秘金鐘,等. BDS與GPS、GLONASS多模融合導航定位時空統一[J]. 大地測量與地球動力學, 2013, 33(4):73-78.

[15] 陳俊勇,楊元喜,王敏,等. 2000國家大地控制網的構建和它的技術進步[J]. 測繪學報, 2007, 36(1):1-8.

[16] 程鵬飛,文漢江,成英燕,等. 2000國家大地坐標系的橢球參數及其與GRS80和WGS84的比較[J]. 測繪學報, 2009, 38(3):189-194.

[17] 魏子卿. 2000中國大地坐標系及其與WGS84的比較[J]. 大地測量與地球動力學, 2008, 28(5):1-5.

[18] 李征航，黃勁松．GPS測量與數據處理[M]．武漢：武漢大學出版社， 2005.