面向資源使用的TTL緩存服務 計費機制與存儲策略

褚偉波,王麗芳,蔣澤軍,范剛龍

(1.西北工業大學計算機學院,710072,西安; 2.洛陽師范學院電子商務學院,471934,河南洛陽;3.洛陽師范學院河南省電子商務大數據處理與分析重點實驗室,471934,河南洛陽)

隨著各類社交網絡以及在線視頻網站等應用的流行,網絡流量呈現出爆炸式增長趨勢[1-2]。未來幾年內,以圖片、視頻、音頻等為代表的多媒體內容傳輸引起的流量還將持續快速增長[3],從而給現有互聯網帶來前所未有的壓力。

網絡緩存是解決大規模內容傳輸性能瓶頸的重要手段。當前普遍采用的內容分發網絡(CDN)[4-5]通過在網絡邊緣部署大量內容緩存服務器把內容就近推送給用戶,避開影響數據傳輸速度和穩定性的瓶頸。近些年提出的內容中心網絡(ICN)[6-8]更是將緩存作為網絡基礎設施的一部分,通過在路由器、交換機上直接部署大容量高速緩存來減輕網絡負載和內容服務器的壓力,提高終端用戶體驗。

作為一種重要的基礎資源,網絡緩存在提升網絡性能方面發揮著重要作用。如同IP網絡中針對用戶的帶寬資源分配和管理對于現有互聯網的基礎作用一樣,網絡緩存資源的分配與管理是未來網絡研究中的一個基礎問題。本文對網絡邊緣TTL(time-to-live)緩存的計費模型與存儲策略進行了研究,提出了基于內容文件緩存命中速率以及內容文件緩存逗留時間的2種TTL緩存計費模型。將TTL緩存的定價與存儲策略問題建模成一個2層的Stackelberg博弈模型[9],并在文件請求到達過程為泊松過程的情況下,分別求解在均一定價和差異定價策略下系統的最優緩存價格以及對應的內容文件緩存時間。利用仿真實驗進一步對比了在不同定價策略和計費模型下緩存服務提供商獲得的投資回報以及內容提供商產生的收益,得到了一些重要結論。提出的模型和得到的結果對于規范網絡緩存市場、激勵緩存服務提供商、提升網絡服務質量以及確保用戶和應用的公平性等多方面具有重要意義。

1 TTL緩存性能分析

網絡緩存通常可以分為內容替換型(replacement-based)緩存和基于TTL緩存2種。內容替換型緩存在一個新的文件到達而又無空余空間時,依據一定的策略(例如LRU、FIFO、RANDOM等)將現有緩存中的文件替換出去;TTL緩存則為每個新到達的內容文件設定一個緩存時間,當緩存時間用完再將內容替換出去。與內容替換型緩存比較,TTL緩存通過對單個內容文件的緩存時間進行設置,不僅可以更加細粒度地控制內容的訪問行為,同時也極大地方便了對緩存性能進行數學分析。

TTL緩存在實現時又可以分成2類。一類是Non-reset TTL緩存,如圖1所示。在這類緩存中,每個內容文件的TTL值在緩存期間保持不變。任何在文件緩存期間到達的請求都會產生一次緩存命中(cache hit),否則產生一次緩存命中失敗(cache miss)。另外一類是Reset TTL緩存,這類緩存中每個文件Fi的TTL值Ti會在每次緩存命中時被重新設置,如圖2所示。對于TTL緩存,通常關注任意文件Fi的如下性能指標:①緩存命中概率(hit probability),表示每一次Fi的請求到來時文件Fi正好存在于緩存中的概率,記為Hi;②文件緩存概率(file occupancy),表示任意時刻Fi存在于緩存中的概率,記為Oi;③緩存逗留時間(sojourn time),表示每一次文件Fi被緩存后存在于緩存中的時間,記為Qi。在Reset TTL緩存中,Qi為一隨機變量,用E[Qi]表示平均逗留時間。

圖1 Non-reset TTL緩存示意圖(單個文件Fi緩存過程)

圖2 Reset TTL緩存示意圖(單個文件Fi緩存過程)

對于TTL緩存,若文件之間相互獨立且每個文件的請求到達過程為泊松過程,有如下關系成立[10-12]

Hi=Oi

(1)

(2)

式中:Ti表示文件Fi的TTL值;λi為Fi請求到達速率。以上公式表明,若已知文件Fi的緩存命中概率Hi,則可以根據式(2)求得Fi在不同類型緩存中的TTL值Ti,本文就是通過求取文件的緩存命中概率來設置它們對應的緩存時間。

2 問題描述和系統建模

2.1 問題描述

考慮一個在網絡邊緣部署了容量為C(可容納內容文件數)的TTL高速緩存的自治系統,該緩存被系統中所有用戶共享。記用戶訪問的內容文件集合為F={F1,F2,…,FN},Fi代表一個內容文件。用戶對于單個文件的請求會先到達TTL高速緩存,若請求文件在緩存中,則產生一次緩存命中,這時目標文件直接從緩存返回給用戶;否則,產生一次緩存命中失敗,目標文件從遠端內容服務器取回,然后再返回給用戶。為了使用緩存服務來提高內容傳輸性能,視頻、社交網絡等內容提供商需要向緩存服務提供商支付一定的緩存使用費用。一般情況下,緩存服務提供商可以向內容提供商發布其緩存服務的價格,由內容提供商決定每個內容文件的緩存時間,緩存服務提供商按照一定標準向內容提供商收取費用。在這樣的模型下,需要解決以下3個問題:①計費機制,即緩存服務提供商對其緩存服務計費的標準或依據是什么?②定價問題,即緩存服務的價格是多少?③存儲策略,即內容提供商每個內容文件的緩存時間是多少?

針對上述問題中的第1個問題,本文提出基于內容文件緩存命中速率和內容文件緩存逗留時間的緩存服務計費機制。內容文件緩存命中速率刻畫了單位時間內用戶訪問一個內容文件產生的緩存命中次數,它從流量(或帶寬)的角度刻畫了資源占用情況;內容文件緩存逗留時間刻畫了一個內容文件在緩存中存在時間的長短,它從存儲空間利用的角度描述了資源占用情況。顯然,這是2種基于實際資源使用的計費標準。對于包括互聯網帶寬在內的多項經濟學研究[13-15]表明,對于服務提供商來說,基于實際資源使用狀況的計費策略往往能夠達到更高的資源利用效率以及投資回報。

2.2 系統建模

為簡化分析,作如下假設:每個內容文件的大小相同,實際中若內容文件大小不一,則可將其分割成多個固定大小的基本文件塊,把每個文件塊當作一個內容文件;與內容文件的緩存時間相比,目標文件從遠端內容服務器下載所需時間可忽略不計;用戶訪問每個內容文件的請求過程為一泊松過程。

由于請求過程為泊松過程,可知Hi=Oi。λiHi為文件Fi的緩存命中速率。此外,假定內容提供商關于每個文件Fi的效益函數是一個關于其緩存命中速率λiHi的連續凹增長函數Ui(λiHi)=wiln(1+λiHi),其中wi為權重系數,反映文件Fi的重要性。在資源分配和管理中,廣泛使用log函數表示效用[16]。

將TTL緩存服務計費與存儲策略問題建模成一個2層的Stackelberg博弈模型[9]:在高層,緩存服務提供商設定一定的緩存價格,使其回報最大;在底層,假定內容提供商是理性的,其根據緩存服務提供商設定的價格設置相應的文件緩存時間,使得自己的收益最大。在Stackelberg博弈模型中,上層參與者具有領導權,因此整個博弈的目標就是使得緩存服務提供商的回報最大化。下面,分別對2種緩存服務計費機制和存儲策略在差異定價和均一定價的情況下進行討論。差異定價指緩存服務提供商可以對不同文件發布不同的緩存價格,而均一定價指所有文件具有相同的緩存價格。

3 TTL緩存服務計費機制與存儲策略

3.1 基于內容文件緩存命中速率的計費機制和存儲策略

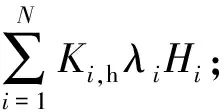
(3)

緩存服務提供商獲得的回報是內容提供商使用緩存的費用,因此它的決策問題可建模成以下優化問題②

(4)

定理1給定緩存價格,內容提供商的決策問題具有唯一的全局最優解。

證明顯然,問題①的目標函數是其決策變量Hi的凹函數。由于Oi=Hi,問題①的約束表明其決策變量空間是一凸集。因此,問題①是一個凸優化問題,存在唯一的全局最優解。

以上結論在泊松請求到達過程的假設下,對于基于緩存命中速率的均一定價策略以及基于緩存逗留時間的均一定價和差異定價策略下均成立,后面將不再贅述。

采用文獻[17]中Stackelberg模型的求解方法,可以得到如下定理。

(5)

(6)

內容提供商關于文件Fi的最優緩存命中概率為

(7)

定理2揭示了以下物理意義:在基于緩存命中速率的差異定價策略下,若文件Fi的請求速率λi越大,則其最優緩存命中概率也越大(見式(7)),對應需要的緩存時間也越多。這意味著TTL緩存傾向于存儲那些熱度比較大的文件。若文件的請求速率一定,Fi的最優緩存價格與其權重系數wi成正比(見式(5),即緩存服務提供商應該對重要的文件收取較高的費用。

3.1.2 均一定價 在均一定價策略下,所有文件具有相同的單位緩存命中速率價格,用Kh表示。內容提供商的決策問題可描述為如下優化問題③

(8)

緩存服務提供商的決策問題④描述如下

(9)

考察內容提供商關于任意文件Fi的收益函數wiln(1+λiHi)-KhλiHi。該函數為凹函數,令Hi(Kh)為使該函數最大化時Hi的取值,得到以下結果

(10)

步驟1將區間(0,wmax]等分成M份,由此得到一系列Kh可能的取值區間,其中M為一較大正整數;

步驟2對于第i個區間[xi,xi+1],計算緩存服務提供商獲得的回報Rh,u(xi)和Rh,u(xi+1);

步驟4比較所有區間上下界,選擇最大回報可能位于的區間,再將這些選擇的區間進行細分;

對比基于緩存命中速率的2種定價策略,發現在差異定價策略下,內容提供商關于文件Fi的最優緩存命中概率只與文件請求速率相關(見式(7)),而在均一定價策略下權重系數wi會影響到文件Fi的最優緩存命中速率。此外,由于實際應用中文件的緩存逗留時間只能在緩存端進行測量,而緩存命中速率可以在用戶端直接測量,因此在相同或相近投資回報的情況下,緩存服務提供商應優先采用基于內容文件緩存命中速率的計費機制。

3.2 基于緩存逗留時間的計費機制和存儲策略

3.2.1 差異定價 假定Ki,s為緩存服務提供商發布的關于文件Fi的單位緩存逗留時間價格。由于只有當請求命中失敗時,文件才會被重新緩存(見圖1和圖2),因此,文件Fi的緩存費用為Ki,sλi(1-Hi)E[Qi]。根據律特法則(Little’s law)[6]可知,Oi=λi(1-Hi)E[Qi]。內容提供商的決策問題⑤可描述如下

(11)

緩存服務提供商決策問題變為以下優化問題⑥

(12)

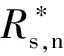
證明已知Oi=Hi。對比問題①②和問題⑤⑥,若再令Ki,s=Ki,hλi,則2個問題完全重合。因此,它們具有相同的最優解。

定理3揭示了如下物理意義:在泊松請求到達的情況下,對于緩存服務提供商來說,基于緩存逗留時間的差異定價策略與基于緩存命中速率的差異定價策略兩者在投資回報和存儲策略方面沒有任何差別,因此考慮緩存命中速率在用戶端容易測量的原因,緩存服務提供商在差異定價策略下,應優先采用基于緩存命中速率的計費機制。

3.2.2 均一定價 假定Ks為緩存服務提供商發布的關于內容文件的單位緩存逗留時間價格。內容提供商的決策問題⑦可描述如下

(13)

緩存服務提供商的決策問題⑧描述如下

(14)

采用與基于內容文件緩存命中速率的均一定價策略相同的分析方法和類似求解方法,可以求解內容文件的最優單位緩存逗留時間價格和緩存服務提供商獲得的最優投資回報,具體分析過程和算法不再贅述。

4 實驗驗證

利用計算機仿真方法對本文模型和策略的有效性進行驗證,并對不同模型和策略進行對比。采用Mosek優化軟件求解在均一定價策略下內容提供商的決策問題③和⑦,并根據求解結果設置不同文件需要的緩存時間。采用定理2中的解析結果選取差異定價策略下的緩存價格和對應的文件緩存時間。實驗過程中假定內容提供商可供訪問的文件數為1 000個,用戶對于這些文件的訪問請求為一速率為105s-1的泊松過程,文件熱度服從參數為0.8的Zipf分布。此外,設置網絡邊緣TTL緩存大小為50(即可容納5%的文件數)。實驗過程中同時記錄緩存服務提供商得到的回報以及內容提供商獲得的收益。

表1給出了緩存系統在文件權重系數相同的條件下(w1=w2=…=wN=1),不同策略的實驗結果,從中可以看出:①在權重系數相同的條件下,基于緩存命中速率、緩存逗留時間的差異定價策略性能優于基于緩存命中速率、緩存逗留時間的均一定價策略,反映出差異定價策略能更好地利用文件在訪問請求熱度方面的差異來提升系統性能;②在基于緩存命中速率、緩存逗留時間的差異定價策略以及基于緩存逗留時間均一定價策略下,內容提供商獲得的收益顯著大于緩存服務提供商得到的回報,而在基于緩存命中速率的均一定價策略下,緩存服務提供商得到的回報高于內容提供商獲得的收益;③對于緩存服務提供商來說,基于緩存命中速率的均一定價策略相比較基于緩存逗留時間均一定價策略能帶來更多的回報,而對于內容提供商來說,基于緩存逗留時間的均一定價策略則比基于緩存命中速率均一定價策略能帶來更多的收益;④由于獲得的收益和回報均為正值,在實際應用中內容提供商和緩存服務提供商都會有采納這些策略的動機和意愿。考慮到緩存命中速率能夠在用戶端進行測量而緩存逗留時間只能在緩存中測量,緩存服務提供商和內容提供商應優先采用基于緩存命中速率的差異定價策略。

實驗中同時考察了文件權重系數不同情況下的系統性能。為此,假定內容提供商的文件按照其重要性隨機分成重要、一般、不重要3類,相應權重賦值為3、2、1,實驗結果見表2。從表2中可以得到和表1一致的結論。此外,對比表1和表2還可以發現,在文件權重系數不同的情況下,差異定價策略相比均一定價策略對于系統性能的提升更為明顯。這也間接反映出差異定價策略能夠非常好地體現文件之間的重要性區別,并更好地利用文件異構性來提升系統性能。在實驗過程中發現,緩存類型對于系統性能幾乎沒有影響。

表1 文件權重相同情況下緩存服務提供商得到的回報和內容提供商獲得的收益

表2 文件權重不同情況下緩存服務提供商得到的回報和內容提供商獲得的收益

5 結 論

緩存是解決互聯網大數據傳輸性能瓶頸的重要技術。本文研究了網絡邊緣TTL高速緩存的計費機制與存儲策略,提出了基于內容文件緩存命中速率以及內容文件緩存逗留時間的兩種計費模型。采用Stackelberg博弈模型對研究問題進行建模,求解了其在均一定價和差異定價策略下緩存服務提供商的最優價格和對應文件的TTL值。仿真實驗進一步對比了在不同定價策略下緩存服務提供商得到的回報和內容提供商獲得的收益,結果表明,本文的模型和策略能夠有效激勵緩存服務提供商和內容提供商,在現實中具有很強的操作性。

參考文獻:

[1] Sandvine. Global internet phenomena report 2H 2012 [EB/OL]. (2012-11-22)[2017-09-26]. https: //www.sandvine.com/hubfs/downloads/archive/2012-2h-global-internet-phenomena-report.pdf.

[2] SHAMMA D A,FRIEDLAND G,ELIZALDE B,et al. YFCC100M: the new data in multimedia research [J]. Communications of the ACM,2016,59(2): 64-73.

[3] Cisco. Cisco visual networking index: forecast and methodology,2014-2019 [EB/OL]. (2015-05-27)[2017-09-26]. http: //s2.q4cdn.com/230918913/files /doc_downloads/report_2014/white_paper_c11-481360.pdf.

[4] Wikipedia. Content delivery network [EB/OL]. (2017 -09-01)[2017-09-26]. https: //en.wikipedia.org/wiki/Content_delivery_network.

[5] PALLIS G,VAKALI A. Insight and perspectives for content delivery networks [J]. Communications of the ACM,2006,49(1): 101-106.

[6] JACOBSON V,SMETTERS D K,THORNTON J D,et al. Networking named content [C]//Proceedings of the International Conference on Emerging Networking Experiments and Technologies. New York,USA: ACM,2009: 1-12.

[7] CHOI J,HAN J,CHO E,et al. A survey on content-oriented networking for efficient content delivery [J]. Communications Magazine IEEE,2011,49(3): 121-127.

[8] 吳超,張堯學,周悅芝,等. 信息中心網絡發展研究綜述 [J]. 計算機學報,2015,38(3): 455-471.

WU Chao,ZHANG Yaoxue,ZHOU Yuezhi,et al. A survey for the development of information-centric networking [J]. Chinese Journal of Computers,2015,38(3): 455-471.

[9] Wikipedia. Stackelberg competition. [EB/OL]. (2017 -01-23)[2017-09-26]. https: //en.wikipedia. org/wiki/Stackelberg_competition.

[10] BERGER D S,GLAND P,SINGLA S,et al. Exact analysis of TTL cache networks [J]. Performance Evaluation,2014,79: 2-23.

[11] FOFACK N C,DEHGHAN M,TOWSLEY D,et al. On the performance of general cache networks [C]//Proceedings of the 8th International Conference on Performance Evaluation Methodologies and Tools. New York,USA: ACM,2014: 106-113.

[12] DEHGHAN M,MASSOULIE L,TOWSLEY D,et al. A utility optimization approach to network cache design [C]//Proceedings of the 2016 IEEE INFOCOM. Piscataway,NJ,USA: IEEE,2016: 1-9.

[13] HONIG M L,STEIGLITZ K. Usage-based pricing of packet data generated by a heterogeneous user population [C]// Proceedings of the 14th Joint Conference of the IEEE Computer and Communication Societies. Piscataway,NJ,USA: IEEE,1995: 867-874.

[14] NEVO A,TURNER J L,WILLIAMS J W,et al. Usage-based pricing and demand for residential broadband [J]. Econometrica,2016,84(2): 411-443.

[15] MA R T. Usage-based pricing and competition in congestible network service markets [J]. IEEE ACM Transactions on Networking,2016,24(5): 3084-3097.

[16] SHEN H,BASAR T. Optimal nonlinear pricing for a monopolistic network service provider with complete and incomplete information [J]. IEEE Journal on Selected Areas in Communications,2007,25(6): 1216-1223.

[17] ZEKRI M,HADJI M,JOUABER B,et al. A Nash Stackelberg approach for network pricing,revenue maximization and vertical handover decision making [C]//Proceedings of the 36th IEEE Conference on Local Computer Networks. Piscataway,NJ,USA: IEEE,2011: 622-629.