沉割槽對滑閥閥芯徑向卡緊力的影響

陸倩倩,阮健,李勝,魯鵬勇

(1.浙江工業大學特種裝備制造與先進加工技術教育部重點實驗室,310014,杭州; 2.浙江大學城市學院,310015,杭州)

閥芯作為液壓滑閥的運動部件,其上所受的液動力、摩擦力等是制約滑閥特性的一個重要的因素,而其所受的徑向不平衡力會產生閥芯卡緊,是影響運動特性關鍵因素之一。近10年來,Amirante[1]運用計算機仿真技術研究了開中心滑閥閥芯上液動力與開口的變化關系并進行了實驗驗證[2];設計了一種閥桿中部增加補償輪廓的比例換向閥閥芯,能夠平衡閥芯上液動力[3]并進行了實驗驗證[4]。王安麟等運用CFD技術研究了滑閥開啟關閉過程中瞬態液動力的影響,并運用參數化建模優化閥芯中部補償輪廓尺寸,為滑閥多學科結構優化奠定了基礎[5];吳小峰等利用計算機流體動力學方法研究了液壓換向閥軸向瞬態液動力的影響因素,同時提供了滑閥內部流道結構參數的優化設計方法[6],但文獻[5-6]方法需要大量的試驗數據,很難從理論上得到結構的最優設計。Lisowski等運用CFD和實驗結合的方法,研究了在閥體上增加內流道的方式,可以在不改閥芯驅動力的情況下提高45%的額定流量[7]。Lisowski等通過設計合理的閥芯幾何結構,運用液動力在比例換向閥中進行壓力補償[8-9],使得閥口射流角僅與閥芯位置相關,與壓力無關,但并未明確油液流動形式、閥芯尺寸及其對閥性能參數的影響。Posa等運用邊界層結合直接數字仿真技術分析了閥的開口量和閥口壓差對流量系數和液動力的影響[10],然而此研究難以通過實驗進行驗證。Guo等研究了大流量閥芯上不平衡力產生滑閥的液動力和閥芯振動,并提出每對閥口結構相同且初始開口或者遮蓋量相等的條件下,可以確保作用在各閥口上液動力平衡[11],但尚未進行實驗驗證。冀宏等研制了非全周開口滑閥壓力分布及噪聲測量實驗裝置[12],通過閥套平移和轉動依次測量不同開度閥口下閥腔壁面壓力分布,并為研究節流槽結構、壓力分布和噪聲間的關系提供實驗平臺,為解決閥口局部壓力測量提供一種有效的方法。以上學者均針對滑閥閥芯運動所受液動力對閥芯軸向受力的影響因素及改進措施。針對徑向卡緊力研究,Hong等設計了一種螺旋槽的滑閥閥芯臺肩[13],用以改善潤滑效果及壓力分布。其他學者[14]也多關注于閥芯臺肩形狀、平衡槽的形狀尺寸及偏心等方面的研究。為了進一步提高液壓閥的功率重量比,減小閥芯運動所需的驅動力,除了上述學者研究方向外,陸倩倩等首次提出在液壓滑閥內部沉割槽由伯努利效應引起的液壓卡緊亦存在,并通過仿真進行系統分析[15],但尚無理論和實驗支撐。因此,為降低傳統滑閥和2D伺服閥[16-17]閥芯啟動時需要克服的卡緊力,研究滑閥閥芯徑向壓力分布及卡緊力的影響因素非常重要。

本文首先通過可視化手段對某滑閥的出口處沉割槽內的流場進行建模和仿真分析,討論沉割槽內流場作用在閥芯臺肩上徑向壓力分布及其影響因素;然后,根據連續性原理和理想的伯努利方程建立了出口截面沉割槽處閥芯臺肩上徑向壓力分布的理論公式,并通過實驗對閥芯臺肩上壓力進行測量,驗證了仿真和理論分析結果,其次,通過徑向壓力分布進行了徑向卡緊力的計算,最后提出一種偏心形式的沉割槽結構并進行了數值仿真驗證。

1 模型建立

1.1 仿真模型

圖1 兩位兩通滑閥結構示意圖

本文以某六通徑兩位兩通滑閥為研究對象,額定流量為60 L/min,結構如圖1所示,其中沉割槽寬度L1為7 mm,槽深e為4 mm,活塞直徑dh為11 mm,活塞環長度Lh為7 mm,活塞桿直徑dg為6 mm,出、入口直徑do、di均為6 mm,工作方式為出口節流。考慮閥腔內結構的對稱性,建立圖1虛線框內閥腔流體域的半剖模型。將三維模型進行四面體網格劃分,同時定義進口、出口、對稱面和壁面,如圖2a所示。將網格導入到Fluent16.0中,定義流動介質為ISO VG 32液壓油,密度為873 kg/m3,黏度為0.027 9 kg/(m·s),選用穩態模擬,及標準的k-ε模型,定義入口形式為流量入口,出口為壓力出口,并且選用SIMPLE算法設置仿真補償和時間。圖2b為出口壓力5 MPa,入口流量為40 L/min的壓力云圖。

(a)模型網格 (b)壓力云圖圖2 仿真模型網格及壓力云圖

1.2 仿真條件及結果

仿真條件設置如下:入口流量Q分別為10 L/min、40 L/min;閥口開度x分別為0.5 mm、2 mm;沉割槽深徑比e/dh分別為0.18和0.36。

在通過出口軸線與閥芯軸線相垂直的截面上,每隔π/6選取閥芯臺肩表面上6個關鍵點,提取不同仿真條件下關鍵點的壓力值,壓力分布曲線如圖3所示,其中右側縱坐標適用于流量為10 L/min的情況。

圖3 理論和仿真結果曲線匯總

由圖3中仿真曲線變化趨勢知閥芯凸肩上關鍵點的壓力值隨流體流向出口的方向遞減。流量越大,壓力遞減的幅度越大。出口壓力為5 MPa,e/dh為0.36,當入口流量為10 L/min和40 L/min時,壓力降低幅值分別為0.010 MPa和0.150 MPa;e/dh越大,壓力遞減幅度越小,入口流量為40 L/min,出口壓力為5 MPa時,e/dh分別為0.18和0.36時,壓力遞減幅值為0.616 MPa和0.150 MPa;且根據文獻[15]中研究可知,壓力變化幅值與出口壓力無關。

2 理論分析

2.1 理論推導

為研究出口節流環槽處閥芯臺肩上壓力分布情況,假設以下5種情況:

(1)忽略圖1模型中入口油液流入滑閥閥桿與閥體區域的影響;

(2)靜態仿真,無壁面滑移;

(3)油液不可壓縮且特性穩定;

(4)忽略壁面上粗糙度及縫隙泄漏;

(5)忽略流動過程的粘性摩擦損失。

流體從滑閥閥桿與閥體構成的同心圓環流入,經節流閥口至沉割槽區域,再匯流至出口流出,如圖4a中箭頭方向所示。為得出沉割槽處閥芯凸肩上壓力分布的理論表達式,選取夾角為dθ的微元為研究對象,如圖4b所示,dθ微元中油液從區域①流入,經過閥口②,到達區域③。

(a)液流方向 (b)微元圖4 模型中液流方向及微元

因滑閥閥口屬于異型流道,其臨界雷諾數為280[18],認為滑閥正常工作均屬于紊流狀態。根據薄壁小孔節流公式,微元中經區域①流經閥口②的流量表達式為

(1)

式中:Cd為流量系數;x為閥口開度,mm;δ為閥芯與閥體間隙,mm;ρ為流體密度,kg/m3。每個dθ對應的區域均有dQ流量流入沉割槽區域③。且在沉割槽壁面的限制下形成漩渦,如圖5所示。根據假設,沉割槽處閥芯臺肩上由漩渦產生的軸向速度相等且會產生能量耗散,當能量耗盡后,沉割槽區域內的油液沿著圖5a中虛線箭頭方向從0經π/2向π方向匯總至出口流出,因此沉割槽內任意θ位置對應的流量為

圖5 沉割槽截面內的漩渦

(2)

理論上,當θ=0時,Q0=0。故沉割槽內任意θ位置的平均流速vθ等于Qθ與該位置沉割槽內通流截面面積Aθ的比值

(3)

根據入口流量Q等于通過節流口的流量

(4)

且理想伯努利方程為

(5)

由式(2)～式(5)可得沉割槽內壓力pθ分布

(6)

由式(6)可以看出,沉割槽內壓力分布與壓力點位置θ、入口流量Q、沉割槽截面尺寸L1和e有密切關系。

2.2 理論解析和仿真對比

圖3為閥口開度x分別在0.5 mm和2 mm、入口流量Q為10 L/min和40 L/min、沉割槽深徑比e/dh等于0.18和0.36情況下關鍵點的壓力分布理論和仿真曲線,曲線隨壓力點位置成拋物線下降的趨勢,壓力值也十分吻合。驗證了式(6)的壓力值隨位置點關系是正確的。

圖6表示出口壓力為5 MPa、e/dh為0.36的情況下,壓力點分別在π/6、π/2和5π/6位置的壓力值隨入口流量變化的仿真曲線。由圖6可見,仿真曲線呈拋物線上升關系,與式(6)中壓力分布隨流量變化趨勢一致。因式(6)中的中括號項在θ∈[0～5π/6]區間,恒大于0,故在理論上關鍵點壓力值隨流量增加呈拋物線上升,且壓力幅值隨著壓力點位置靠近出口而逐漸減小。

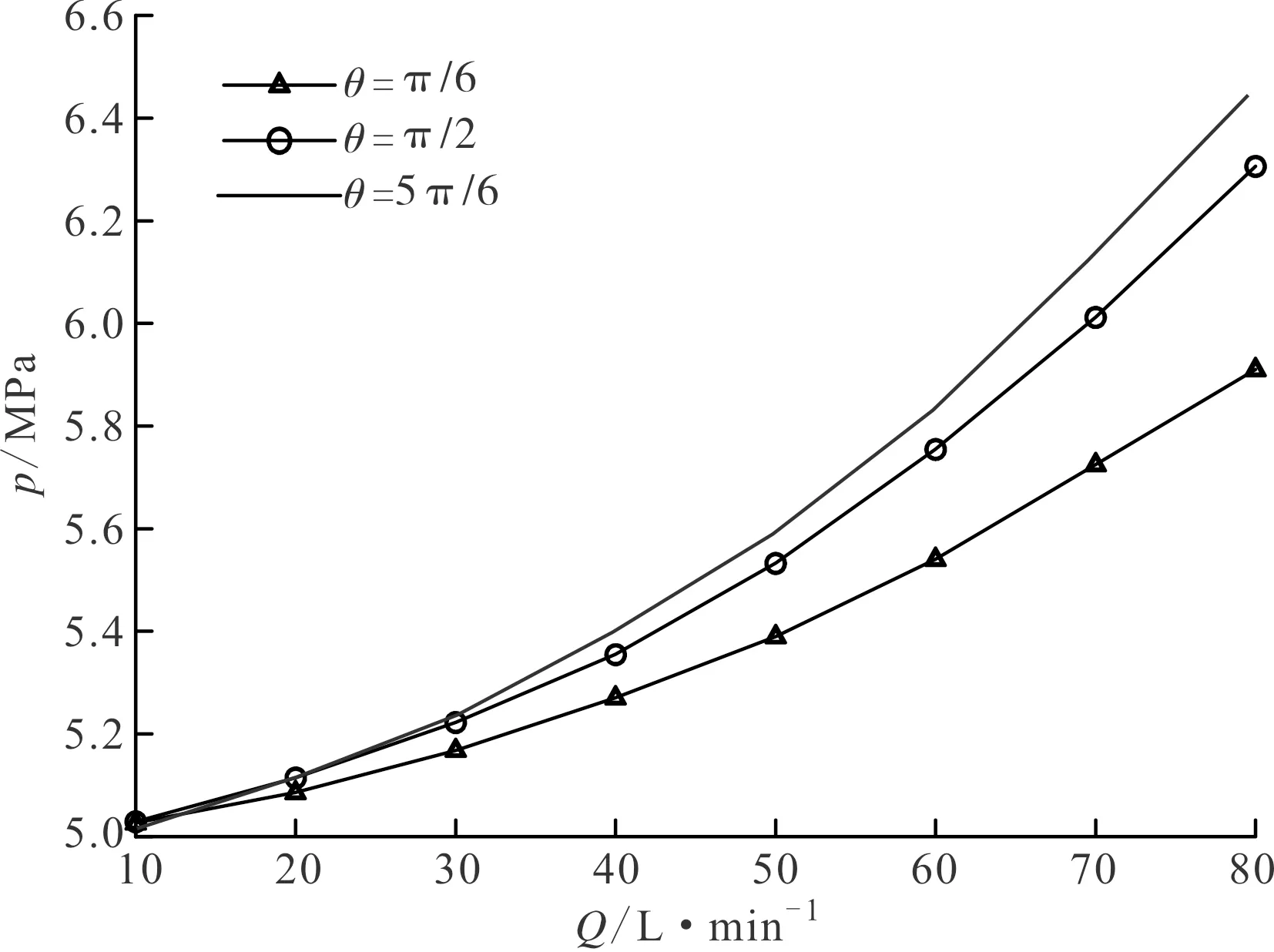
圖6 不同流量下同一位置點的壓力分布曲線

圖7 40 L/min時沉割槽不同深度同一位置的壓力分布曲線

圖8 10 L/min時沉割槽不同寬度同一位置的壓力分布曲線

圖7和圖8為相同入口流量和閥口開度下,不同沉割槽尺寸的壓力分布仿真曲線。圖7是在入口流量為40 L/min,沉割槽寬度為7 mm的情況下,深度為4、5、6、7和8 mm這5種情況下,關鍵點位置在0、π/2、2π/3和5π/6下的壓力分布仿真曲線;圖8是入口流量為10 L/min,沉割槽深度為4 mm情況下,寬度為7、8、9和10 mm這4種情況下,閥芯臺肩關鍵壓力點位置在π/6、π/2、2π/3和5π/6時的壓力分布仿真曲線。由圖7、圖8可見,壓力分布隨沉割槽深度和寬度近似成二次冪函數分布,與理論公式中的關系吻合。

綜上,通過理論和仿真結果對比得出,關鍵點的壓力值與壓力點位置呈二次多項式函數下降關系,與入口流量、沉割槽寬度和深度均呈二次多項式函數上升。由圖5～圖8可以得出,入口流量、關鍵點位置及沉割槽尺寸對壓力分布影響與式(6)中各參數之間影響關系在理想情況下非常吻合,故式(6)在理想情況下可作為計算沉割槽處閥芯臺肩徑向壓力的參考公式。

3 實驗驗證

3.1 實驗臺架

圖9 實驗臺原理示意圖

圖10 實驗測試現場圖

為了驗證沉割槽內關鍵點的壓力分布,搭建原理如圖9所示的實驗系統。系統主要由液壓泵站、傳感器、采集卡和計算機等組成,測試現場如圖10所示。被測試的對象使用3D成型技術制作出固定開口(x=0.5 mm)的6個被試閥,被試閥內部尺寸與仿真模型尺寸相同,每個被試閥引出一個位置的測壓油道,即6個被測閥的測壓油道分別對應θ=0、θ=π/6、θ=π/3、θ=π/2、θ=2π/3和θ=5π/6,且測壓油道尺寸相同。圖11是測壓油道位置在θ=0位置時的剖分圖。測壓油道通過轉接閥塊引出測壓口,連接壓力傳感器(Huba 511.940003142,0～6 MPa),如圖10。通過NI 6361采集卡將壓力信號傳至計算機,上位機使用LabVIEW2014編寫的通用采集程序,以單通道1 kHz的采樣頻率,并將各通道信號濾波、平均及量綱轉換后作為被測點的壓力值。

圖11 3D成型閥剖面圖

3.2 實驗結果

圖12 0位置壓力隨流量變化的仿真和實驗曲線

實驗過程中,被試閥的入口流量從19 L/min逐漸增加至40 L/min,記錄關鍵點隨流量變化的壓力值。圖12為測壓點在0位置時的壓力分布與入口流量的關系,實驗和仿真壓力隨流量變化趨勢一致性很好。圖13是入口流量在40 L/min下,關鍵點位置從0到5π/6變化時的壓力分布實驗和仿真結果,驗證了壓力值隨測壓點從遠離出口到靠近出口附近逐漸下降。

圖13 40 L/min時閥芯臺肩周向壓力分布仿真和實驗曲線

4 閥芯臺肩徑向卡緊力分析

忽略閥芯臺肩上軸向壓力分布不均,且模型關于對稱面(X=0)對稱,僅討論Y方向徑向力。根據式(5),將臺肩徑向壓力與其所在微元弧面積相乘后沿Y軸方向進行投影,得到微元上閥芯臺肩所受的徑向力沿Y軸的分力為

dFy=0.5Pθ(L1-x)dhcosθdθ

(7)

將dFy在θ∈[0～5π/6]范圍內進行積分,得Y軸方向上徑向卡緊力

(8)

由式(6)可得:當入口流量為10 L/min和40 L/min時,開口量為0.5 mm,L1=7 mm,e=4 mm的情況下Y方向的徑向合力分別為0.26 N和4.2 N;當沉割槽深度e=2 mm時,入口流量為40 L/min時,Fy=14.47 N。由此可知,閥芯臺肩上因伯努利效應產生的徑向壓力不均會產生徑向卡緊力,且流量越大,徑向卡緊力越大;沉割槽深度越淺,徑向卡緊力急劇增加。

5 沉槽結構優化分析

5.1 駐點及臺肩徑向壓力分布

(a)測壓點及駐點位置 (b)閥芯臺肩徑向壓力分布圖14 閥芯臺肩測壓點駐點位置及徑向壓力分布

由上文知沉割槽處閥芯臺肩在關鍵點上的壓力從0到5π/6處逐漸下降,如圖14a中的1區,且在0位置,因流速接近為零,故壓力達到最大,為駐點。但是,閥芯臺肩正對出口處的壓力因對流和流速方向變化會產生駐點2,故此位置的壓力也會急劇增加到最大值。圖14b表示入口流量為40 L/min,出口壓力為5 MPa,0.5 mm開口的仿真結果的壓力分布趨勢。因閥腔結構關于X=0對稱,故X軸方向的壓力對稱分布,即徑向壓力不平衡主要分布在Y軸方向。

將各位置壓力值沿Y軸方向投影的代數和Δpy與此情況下徑向壓力最大值pmax的比值作為衡量壓力沿Y軸分布的不均勻度ε,計算公式如下

(9)

式中:ε=0,表示壓力沿Y軸徑向力平衡。在圖14b的仿真條件下,根據式(7)計算可得ε=0.13,正值表示壓力合成沿Y軸正方向。

5.2 沉割槽外壁輪廓優化及分析

由式(6)知,沉割槽處閥芯臺肩上的壓力分布與沉割槽截尺寸有關,當沉割槽寬度L1固定,假設關鍵點壓力pθ相等,可反推出任意位置沉割槽深度eθ的變化方程。并得出無徑向壓力不均勻沉割槽壁面理論輪廓的極徑r表達式

(10)

取原同心圓環與無徑向壓力不均勻的理論輪廓軌跡所對應的閥腔體積相等,且活塞直徑相同,當入口流量為40 L/min時,根據下式確定0位置的最小深度e0

(11)

根據式(11)可得e0=2.89 mm。無徑向壓力不均理論輪廓如圖15a所示,這種阿基米德螺線輪廓加工困難,故嘗試采用偏心圓進行輪廓逼近,如圖15b,沉割槽(偏心圓)內徑19 mm,偏心3.5 mm。

(a)A沉割槽 (b)B沉割槽圖15 兩種沉割槽的輪廓

將偏心圓模型進行流體動力學仿真,在出口壓力為5 MPa、入口流量分別為40 L/min和60 L/min、開口0.5 mm情況下得到壓力分布曲線如圖16所示。

圖16 同心和偏心沉割槽結構閥芯上壓力分布曲線

圖16中偏心形式沉割槽內的閥芯表面壓力分布近似關于Y=0對稱,將4組曲線對應的壓力值代入式(7)中,得到不均勻度ε如表1所示。顯然,偏心沉割槽內的閥芯臺肩上壓力不均勻度在40 L/min和60 L/min情況下,相對同心形式分別提高了64%和87%,故徑向卡緊力亦相應減小。且偏心結構并未改變閥芯凸肩與閥體配合長度,故泄漏量不會因沉割槽結構變化增加;同時,閥芯凸肩尺寸未變,流經閥口產生的壓力損失也不會改變。

表1 同心和偏心沉割槽處閥芯臺肩的壓力不均勻度

6 結 論

(1)運用流體仿真軟件對出口處沉割槽內閥芯臺肩上的壓力分布進行分析,研究了徑向壓力分布不均勻程度的影響因素,并通過解析和實驗的方法進行驗證;

(2)出口沉割槽處閥芯臺肩上的徑向壓力值隨壓力點位置靠近出口呈平方關系下降;且壓力不均分布會產生徑向卡緊力,卡緊力值與流量的平方呈正比;沉割槽深度越淺,卡緊力越大。

(3)理論和仿真分析結果表明,在沉割槽內外壁直徑相同的情況下,采用偏心形式可以有效的降低沉割槽處閥芯臺肩上的壓力分布不均勻度,為減小閥芯卡緊力提供了新型閥腔結構的設計思路。

參考文獻:

[1] AMIRANTE R,VESCOVO G D,LIPPOLIS A. Evaluation of the flow forces on an open centre directional control valve by means of a computational fluid dynamic analysis [J]. Energy Conversion and Management,2006,147: 1748-1760.

[2] AMIRANTE R,VESCOVO G D,LIPPOLIS A. Flow forces Analysis of an open center hydraulic directional control valve sliding spool [J]. Energy Conversion and Management,2006,47: 114-131.

[3] AMIRANTE R,MOSCATELLI P G,CATALANO L A. Evaluation of the flow forces on a direct proportional valve by means of a computational fluid dynamic analysis [J]. Energy Conversion and Management,2007,48: 942-953.

[4] AMIRANTE R,DISTASO E,TAMBURRAN P. Sliding spool design for reducing the actuation forces in direct operated proportional directional valves: Experimental validation [J]. Energy Conversion and Management,2016,119: 399-410.

[5] 王安麟,吳小鋒,周成林,等. 基于CFD的液壓滑閥多學科優化設計 [J]. 上海交通大學學報,2010,44(12): 1767-1772.

WANG Anlin,WU Xiaofeng,ZHOU Chenglin,et al. Multidisciplinary optimization of a hydraulic slide valve based on CFD [J]. Journal of Shanghai Jiaotong University,2010,44(12): 1767-1772.

[6] 吳小鋒,干為民,劉春節,等. 液壓換向滑閥內部結構的健壯性設計 [J]. 中國機械工程,2015,26(15): 2030-2040.

WU Xiaofeng,GANG Weimin,LIU Chunjie,et al. Robust design of hydraulic slide valve internal structure [J]. China Mechanical Engineering,2015,26(15): 2030-2040.

[7] LISOWSKI E,CZYZYCKI W,RAJDA J. Three dimensional CFD analysis and experimental test of flow force acting on the spool of solenoid operated directional control valve [J]. Energy Conversion and Management,2013,70: 220-229

[8] LISOWSKI E,FILO G,RAJDA J. Pressure compensation using flow forces in a multi-section proportional directional control valve [J]. Energy Conversion and Management,2015,103: 1052-1064.

[9] LISOWSKI E,FILO G. CFD analysis of the characteristics of a proportional flow control valve with an innovative opening shape [J]. Energy Conversion and Management,2016,123: 15-28.

[10] POSA A,ORESTA P,LIPPOLIS A. Analysis of a directional hydraulic valve by a Direct Numerical Simulation using an immersed-boundary method [J]. Energy Conversion and Management,2013,65: 497-506.

[11] GUO Haiping,LI Baoren,YANG Gang. Study on the influence of flow force on a large flowrate directional control valve [C]// 6th IFAC Symposium on Mechatronic Systems. Laxenburg,Austria: The International Federation of Automatic Control Secretariat,2013: 469-477.

[12] 冀宏,傅新,楊華勇,等. 非全周開口滑閥壓力分布測量研究 [J]. 機械工程學報,2004,40(4): 99-102.

JI Hong,FU Xin,YANG Huayong,et al. Measurement on pressure distribution of Non-circular opening spool valve [J]. Chinese Journal of Mechanical Engineering,2004,40(4): 99-102.

[13] HONG S H,KIM K W. A new type groove for hydraulic spool valve [J]. Tribology International,2016,103: 629-640.

[14] 羅艷蕾,吳健興,陳倫軍,等. 基于CFD的液壓滑閥閥芯均壓槽的研究 [J]. 液壓氣動與密封,2013(1): 13-15.

LUO Yanlei,WU Jianxing,CHEN Lunjun,et al. The research of the Pressure-equalizing grove for hydraulic slide valve based on CFD [J]. Hydraulics Pneumatics & Seals,2013(1): 13-15.

[15] 陸倩倩,阮健,李勝. 伯努利效應引起滑閥閥芯徑向力的研究 [J]. 中國機械工程,2017,28(19): 2332-2338.

LU Qianqian,RUAN Jian,LI Sheng. Research of the radial pressure for hydraulic slide valve caused by Bernoulli effect [J]. China Mechanical Engineering,2017,28(19): 2332-2338.

[16] 童成偉,阮健,孔晨菁,等. 2D電液轉閥式換向閥閥芯卡緊力分析 [J]. 液壓氣動與密封,2016(4): 5-8.

TONG Chengwe,RUAN Jian,KONG Chenjing,et al. Analysis of the clamping force for 2D electro-hydraulic rotary valve [J]. Hydraulics Pneumatics & Seal,2016(4): 5-8.

[17] 劉國文,阮健,李勝,等. 2D電液比例換向閥閥芯卡緊力分析 [J]. 中國機械工程,2015,26(15): 1995-1999.

LIU Guowen,RUAN Jian,LI Sheng,et al. Analysis of spool clipping force for 2D electro-hydraulic proportional directional valve [J]. China Mechanical Engineering,2015,26(15): 1995-1999.

[18] 盛敬超. 液壓流體力學 [M]. 北京: 機械工業出版社,1980: 120.