改進加權SVC的雷達信號分選新方法*

袁澤恒，田潤瀾,張旭洲

(空軍航空大學 航空作戰勤務學院，吉林 長春 130022)

0 引言

雷達輻射源信號分選是將雷達偵察接收機截獲的多部雷達信號，分成單部雷達信號的過程，是電子偵察系統和電子支援系統中的核心與關鍵[1]。傳統的雷達輻射源信號分選主要基于脈沖重復間隔(PRI)以及其改進算法[2-3],當前也有利用脈沖到達時間差TDOA的分選方法[4]，隨著雷達體制和電磁環境的日益復雜，基于PRI和TDOA的雷達信號分選正確率低。利用脈沖參數如載頻(CF)、脈寬(PW)、脈幅(PA)、到達方向(DOA)[5-6],預先設定好一定的容差，經過多層次的相關處理，完成信號分選的結果可靠性差，而且產生增批的問題嚴重[7]。

為了克服上述方法的問題，基于多參數的雷達信號聚類分選得到廣泛應用[8]，聚類是一種無監督的分類，不需要先驗知識，有利于對未知雷達信號進行分選，彌補了現有雷達庫數據不全的短板。常用的聚類方法有K-means方法[9]、模糊聚類方法[10]等，這些方法普遍存在復雜度高、類內耦合度和類間分離度低，導致分選結果準確率不高。

支持向量聚類(support vector clustering,SVC)是一種最為有效的無監督非參數型聚類方法[11-12]，但其算法的復雜度高，控制其聚類邊界的參數懲罰因子C和高斯核寬度q的最優選取存在人為因素的影響。文獻[11]采用支持向量聚類和分層互耦的算法，并結合熵的特征進行信號分選，但是熵的特征不是穩定的物理量，尤其是在識別聚類結果復雜度的時候，閾值的設置存在人為因素的影響。本文在文獻[11]方法的基礎上對數據樣本和核函數內積進行加權，建立聚類結果有效評價模型，采用穩定的物理量作為聚類結果的度量值，提高分選的準確率。

1 支持向量聚類算法

支持向量聚類算法的基本原理是[13]：利用Gaussian核函數，將數據樣本映射到一個高維特征空間中，并在這個高維特征空間中尋找一個能包圍所有樣本數據映射點的最優超球面，將這個超球面反映射回數據空間，最終得到包含所有數據點的等值線集。支持向量聚類(SVC)通過基于核函數的非線性映射，能夠較好的分辨、提取并放大有用特征，融入松弛量后能有效排除孤立點和離群值，實現更為準確的聚類。

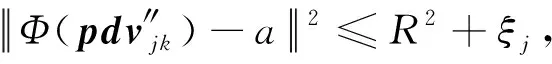
(1)

式(1)的Lagrangian函數為

(2)

式中:βj和μj均大于0，為Lagrangian乘子；常數C稱為懲罰因子。

結合KKT條件，得出式(2)的Wolfe對偶形式：

(3)

引入Gaussian核函數：

(4)

式中：q為Gaussian核的寬度參數。

將核函數帶入式(3)中得

(5)

對于每一個標準化的脈沖描述數據向量pdv″，其映射到特征空間中的像到球心的距離表示為

(6)

式中:當{pdv″|R(pdv″)=R}時，這時的標準化脈沖描述向量稱為支持向量(SV)。由SV組成的等高面，能確定屬于同一雷達輻射源參數的聚類邊界。此后建立聚類標識關聯矩陣，通過深度最優搜索(DFS)算法根據關聯矩陣進行聚類分配。

在高脈沖密度的環境下，采用支持向量聚類進行分選，就會造成進行運算時關聯矩陣規模龐大的問題，極大程度地降低其運算速度。文獻[11]采用基于支持向量機的分層互耦聚類方法，對數據樣本進行分層處理，很好地解決了上述問題。由于熵是不穩定的物理量，所以文獻[11]采用類型熵調整聚類分選參數，會影響最優分選參數的選取，而且當雷達信號嚴重交疊時，采用文獻[11]的方法進行分選的正確率顯著下降。針對上述方法的不足，對其進行改進。

2 改進支持向量聚類

首先采用極值標準化對雷達信號數據進行預處理，將待聚參數標準化到同一維度上形成數據樣本；然后利用變精度粗糙集計算數據樣本的權重，對數據樣本和支持向量機的核函數內積進行加權，穩定數據樣本之間的平衡，從而避免聚類分選結果被參數的弱相關特征影響；最后對聚類結果進行分析，構建有效地評價模型，引入穩定的物理量來調整聚類分選參數，選取最優的聚類分選參數，提高分選的正確率。

2.1 參數標準化

DOA取值相對穩定，在分選時間內不會發生突變。因此通過已知雷達參數匹配后的數據進一步得到稀釋。在脈沖描述字PDW中，CF和PW也相對穩定可以作為聚類參數。本文將雷達信號的到達角、載頻和脈寬構成一個具有三維信息的雷達脈沖描述向量PDVi，i=1,2,…,n(n為總脈沖個數)。

原始的PDVi比較復雜，為排除原始PDVi中變量之間的量度不同對聚類效果的影響，需要對原始的PDVi進行標準化處理，使不同的參數分布在相同的區間[0,1]內，以相同的量級參與聚類。

對于n個脈沖信號，有m維特征參數，此時樣本數據可以用如下表達式表示，脈沖描述向量PDVi=(pdvi1,pdvi2,…,pdvim)，這里m=3，PDVi=(DOAi,CFi,PWi)。先求出n個樣本數據的第k維數據的均值和標準差為

(7)

(8)

其中，1≤k≤m，由此可得樣本脈沖向量的標準化值

(9)

此時脈沖描述向量的標準化值不一定在區間[0,1]內，采用極值標準化公式：

(10)

2.2 加權處理支持向量聚類

針對不同類型的裝備，測向精度和測頻精度存在很大差異，不同類參數之間差異比較明顯。同一類參數也存在類似問題，比如脈寬過窄，參數測量往往不準確，寬脈沖的區分度好，應當加大權重。對于上述問題，在SVC算法過程中為了降低弱相關對聚類結果準確性的影響，采用變精粗糙集對標準化后的樣本數據進行處理，然后對核函數的內積進行加權[14]。

粗糙集理論中依賴度的定義：

(11)

式中：ci為屬性參數；U為樣本集序號;d為條件屬性;β為誤差參數。

將上述依賴度作為信號參數的重要度，即

(12)

該信號參數的權重為

(13)

在本文中只研究雷達信號輻射源的3個參數，即到達角、載頻、脈寬。所以得到最優特征加權矩陣即

(14)

式中：aDOA，aCF，aPW分別為對應參數重要程度的加權系數。

SVC算法的加權計算公式如下：

(15)

考慮到雷達各輻射源屬性，提高聚類結果的準確率，消除人為設置權重的影響，本文利用變精度粗糙集獲取雷達輻射源各屬性特征參數權重[15]，構成最優特征加權矩陣，該加權矩陣通過輻射源數據確定，完全利用了輻射源數據自身的特征，因此更加適用實際中雷達信號的聚類分選。

將式(14)中上述參量帶入式(15)中可得

(16)

2.3 改進的支持向量聚類分選流程

在雷達輻射源信號分選中，所需處理的數據量很大，極大的影響其運算速度。文獻[11]采用了支持向量機的分層互耦聚類方法，來解決此類問題。本文在文獻[11]方法的基礎上進行改進，具體步驟如圖1所示。

從圖1中可以看出，采用變精度粗糙集從已知雷達知識庫中提取的樣本信息進行分析，得到{DOA,CF,PW}各屬性參數的最優特征加權矩陣，運用到支持向量機的核函數內積上，對其進行加權。此方法不會增加算法的時間復雜度，因為得到最優特征加權矩陣的步驟是事先完成的，所以不會延長聚類分選的時間。

2.4 聚類分選參數調節

本文將標準化處理的樣本數據，脈沖描述向量pdv″作為研究對象，從類內耦合度和類間分離度出發，建立聚類結果有效評價模型，對聚類結果進行分析，從而確定最佳的聚類分選參數q和C。

類內耦合度通過聚類分選后樣本的方差反映，方差越小，樣本間波動就越小，即類內之間樣本緊密程度就越高。

類內耦合度定義為

(17)

式中：ni為樣本數，i為樣本脈沖描述向量的維數。

對應的聚類分選后的樣本中心為

(18)

分離度反映了不同類之間的差異性，定義為

(19)

(20)

分別將類內耦合度和類間分離度除以相應的權值，然后將兩參數進行比較分析，建立對聚類分選結果的有效性評價模型：

(21)

式中：Cλ為對應閾值λ的類數。

G值越大，說明類與類之間的差異越大，聚類分選的結果也就越好。支持向量的聚類分選過程中，其聚類的邊界受Gaussian核的寬度參數q和Lagrangian函數的懲罰因子C的控制。隨著參數q的增加，聚類邊界表現出更緊的特性。通過參數C的減少可以平滑聚類邊界。采用文獻[13]的分裂聚類方法，首先確定參數q的初始值為

(22)

在q的初始值下，會使Gaussian核函數的值偏大，導致聚類分選結果產生單一的聚類。在這種情況下取參數C=1，然后增大參數q的值，這樣，單一的聚類開始分裂。隨著q值增大到一定程度，聚類邊界會變得粗糙，這時通過減少C值，用來平滑聚類邊界。

文獻[13]的方法面臨的問題是如何確定最終的聚類分選結果，確定什么時候停止對聚類的分裂。文獻[11]中利用類型熵隨著信號復雜度的增加而增加的特點，進而對聚類結果分析，來確定最佳的聚類分選參數q和C的值，但是類型熵不是很穩定的物理量，所以采用類型熵調整聚類分選參數誤差較大。為了解決上述問題，本文采用構建的有效性評價模型的參數G來保證門限確定的合理性，通過對多組聚類分選結果G值的計算，識別出較好的聚類分選結果，從而對其進行分析判斷，來確定最佳的聚類分選參數q和C。

3 仿真實驗結果及分析

為了驗證本文方法的優勢和有效性，對上述改進的多參數聚類分選系統進行了仿真實驗。雷達參數的仿真數據如表1所示。

從表1中可以看出，4部雷達在不同屬性的維度上均有重疊或部分重疊，而且雷達樣本2和雷達樣本3在到達角和脈寬參數上重疊比較嚴重，運用常規的分選方法，不僅不能使各雷達輻射源信號完全分開，還會產生信號大量增批和漏批的問題，從仿真數據中隨機抽取400個樣本，分別采用文獻[11]的方法和本文上述方法進行聚類分選，實驗仿真得出三維屬性的雷達樣本信號聚類結果分布圖，如圖2,3所示。

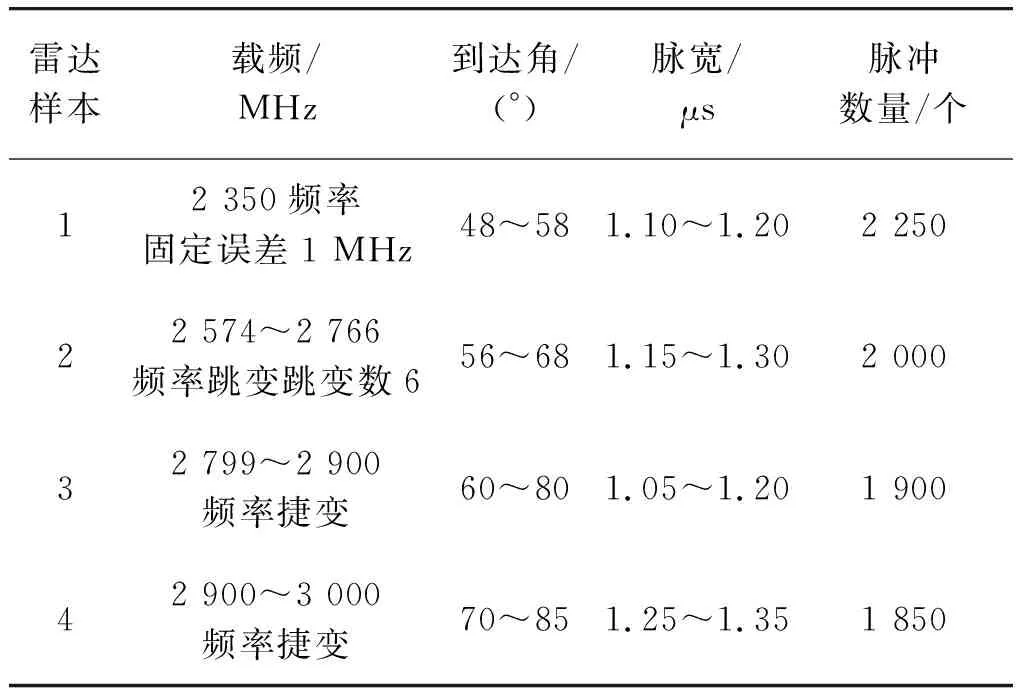
表1 雷達樣本參數信息

可以從圖2中直觀地看出，在雷達樣本2和雷達樣本3的到達角和脈寬樣本數據存在嚴重交疊的時，采用文獻[11]的方法進行聚類分選的結果不夠理想。

文獻[11]是基于支持向量聚類和分層互耦的算法，并引入類型熵來調整聚類分選參數。從表2可以看出，這種方法對不交疊的或者部分交疊的信號，分選正確率高，當信號參數存在嚴重交疊的情況時，分選正確率會明顯降低，而且引入的類型熵不是很穩定的物理量，用來調整分選參數存在一定的偏差。所以采用文獻[11]的算法對仿真數據進行處理時，正確率只有96.8%。本文對上述方法進行了改進，首先對樣本數據進行標準化，采用變精度粗糙集得出各屬性參數的權值，對數據樣本和支持向量的核函數內積進行加權，提高算法的魯棒性，雖然這些都是預先完成的，不會增加算法的完成時間，但是增加了算法的計算量；然后建立對聚類結果的評價模型，引入穩定的參數G，調整最佳的聚類分選參數，提高分選的正確率，從表2中可以看出，本文方法對仿真數據進行處理時，正確率達到99.5%，可以驗證改進算法的有效性。

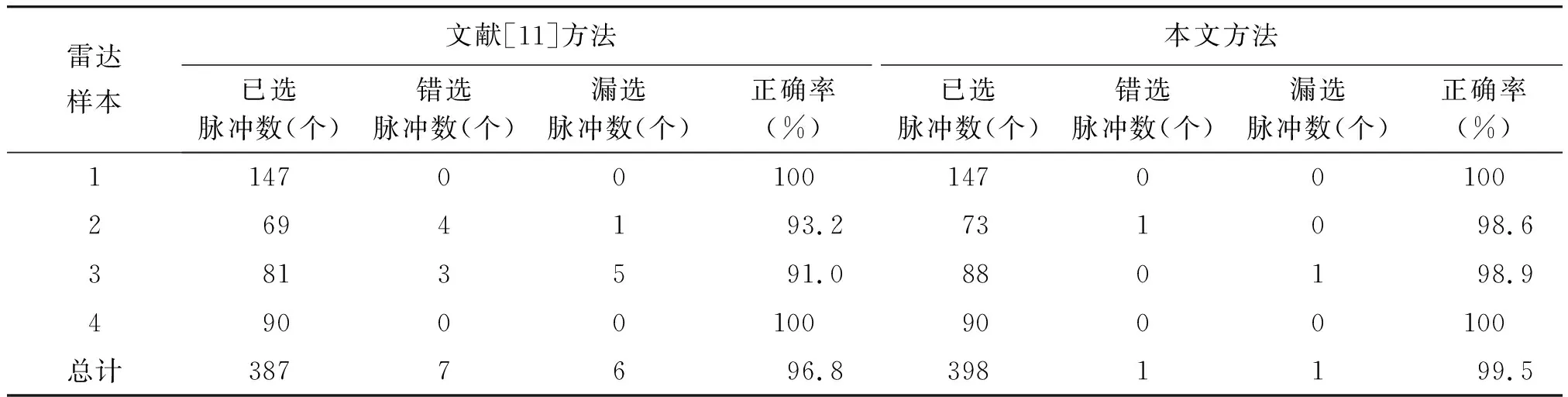
表2 2種方法的分選結果

4 結束語

本文通過采用變精度粗糙集，充分利用各屬性參數自身的特點，獲取各屬性參數的權重，由其構成加權矩陣對雷達樣本和SVC算法中的核函數內積進行加權，解決了數據之間存在不平衡和離群點的問題，從而避免被參數的弱相關特征影響其聚類分選結果。這個過程需要依賴數據庫提前進行，雖然不增加算法的時間復雜度，但是算法的實時性不強。其次本文還通過構建有效評價模型，建立穩定的物理量調整聚類參數。仿真實驗的結果驗證了，當雷達信號嚴重交疊時，采用本文方法進行聚類分選時的正確率高，但是本文算法還存在很多不足，比如算法的復雜度高、時效性差、對數據庫依賴性強等，下一步還需提高算法的時效性。

參考文獻：

[1] 李合生,韓宇,蔡英武,等.雷達信號分選關鍵技術研究綜述[J].系統工程與電子技術,2005,27(12):2036-2039.

LI He-sheng,HAN Yu,CAI Ying-wu,et al.Overview of the Crucial Technology Research for Radar Signal Sorting[J].Systems Engineering and Electronics,2005,27(12):2036-2039.

[2] NISHIGUCHI K ,KOBAYASHI M．Improved Algorithm for Estimating Pulse Repetition Intervals[J].IEEE Trans on AES,2000,36(2):407-421．

[3] 劉旭波,司錫才.雷達信號分選實現的新方法[J].系統工程與電子技術,2010，32(1):53-56.

LIU Xu-bo,SI Xi-cai.New Method for Sorting Radar Signals[J].Systems Engineering and Electronics,2010,32(1):53-56.

[4] 鄭惠文,黃建沖.利用脈沖TDOA的雷達信號分選方法[J].現代防御技術,2017,45(2):217-222.

ZHENG Hui-wen,HUANG Jian-chong.Radar Signal Sorting Method Utilising Pulse TDOA[J].Modern Defence Technology,2017,45(2):217-222.

[5] 何明浩.雷達對抗信息處理[M].北京:清華大學出版社,2010.

HE Ming-hao.Radar Countermeasure Information Processing[M].Beijing:Tsinghua University Press,2010.

[6] 王宇.未知雷達信號PRI的快速分選識別算法研究[D].西安:西安電子科技大學,2010.

WANG Yu.Fast Sorting and Recognition Algorithm of Unknown Radar Signal PRI [D].Xi’an:Xidian University,2010.

[7] 趙葆昶,彭世蕤,郁春來,等.基于相參特性的雷達信號分選中“增批”問題研究[J].現代防御技術,2011,39(4):70-74.

ZHAO Bao-chang,PENG Shi-rui,YU Chun-lai,et al.Research on Increasing-Batch Problem in the Progress of Sorting of Signals Based on Coherency[J].Modern Defence Technology,2011,39(4):70-74.

[8] 郭杰,陳軍文.一種處理未知雷達信號的聚類分選方法[J].系統工程與電子技術,2006,28(6):853-856.

GUO Jie,CHEN Jun-wen.Clustering Approach for Deinterleaving Unknown Radar Signals[J].Systems Engineering and Electronics,2006,28(6):853-856.

[9] 聶曉偉.基于K-Means算法的雷達信號預分選方法[J].電子科技,2013,26(11):55-58.

NIE Xiao-wei.Radar Signal Pre-Sorting Based on K-Means Algorithm[J].Electronic Science and Technology,2013,26(11):55-58.

[10] 尹亮,潘繼飛,姜秋喜.基于模糊聚類的雷達信號分選[J].火力與指揮控制,2014,39(2):52-57.

YIN Liang,PAN Ji-fei,JIANG Qiu-xi.A Study on Sorting of Radar Signals Based on Fuzzy Clustering[J].Fire Control & Command Control,2014,39(2):52-57.

[11] 國強,王常虹,李崢.支持向量聚類聯合類型熵識別的雷達信號分選方法[J].西安交通大學學報,2010,44(8):63-67.

GUO Qiang,WANG Chang-hong,LI Zheng.Support Vector Clustering and Type-Entropy Based Radar Signal Sorting Method[J].Journal of Xi′an Jiaotong University,2010,44(8):63-67.

[12] 王世強,張登福,畢篤彥,等.基于快速支持向量聚類和相似熵的多參數雷達信號分選方法[J].電子與信息學報,2011,33(11):2735-2741.

WANG Shi-qiang,ZHANG Deng-fu,BI Du-yan,et al.Multi-Parameter Radar Signal Sorting Method Based on Fast Support Vector Clustering and Similitude Entropy[J].Journal of Electronics and Information Technology,2011,33(11):2735-2741.

[13] BEN-HUR A,HORN D,SIEGELMANN H T,et al.Support Vector Clusteing[J].Journal of Machine Learning Research,2001,2(2):125-137.

[14] 吳連慧,秦長海,宋新超.基于加權SVC和K-Mediods聯合聚類的雷達信號分選方法[J].艦船電子對抗,2017,40(1):13-17.

WU Lian-hui,QIN Chang-hai,SONG Xin-chao.Radar Signal Sorting Method Based on Weighting SVC and K-Mediods Combined Clustering[J].Shipboard Electronic Countermeasure,2017,40(1):13-17.

[15] 孫士保.變精度粗糙集模型及其應用研究[D].成都:西南交通大學,2005.

SUN Shi-bao.Study on Variable Precision Rough Set Model and Its Application[D].Chengdu:Southwest Jiaotong University,2005.