考慮邊界條件不確定性的地下水污染風險分析

李久輝,盧文喜*,辛 欣,羅建男, 常振波 (1.吉林大學地下水資源與環境教育部重點實驗室,吉林長春 130021；2.吉林大學環境與資源學院,吉林 長春 130021)

早期研究中,確定性污染質運移數值模擬模型通常用來預測地下水污染質運移情況,確定性模擬模型未考慮輸入模擬模型參數和邊界條件的不確定性,輸入模型參數及邊界條件均為定值,其輸出結果與輸入對應且確定唯一,依靠其確定結果難以評估模擬模型輸出結果的可靠程度,致使決策者面臨決策失敗的風險[1].故將輸入模型參數和邊界條件的不確定性引入研究,對于預測地下水污染質運移有重要意義[2].

地下水污染風險分析研究層見疊出,但諸多研究將數學模型處理為確定性模型,忽略了輸入數值模擬模型參數、邊界條件的不確定性.尤其,對于考慮邊界條件不確定性的研究更是寥寥無幾.近些年來,不確定性分析的發展可謂方興未艾.吳吉春等[3]分析了地下水模型不確定性的來源和分類,并且,對不確定性的來源和模型輸出的不確定性進行了討論,提出了地下水模擬不確定性分析的發展前景. Guillaume等[4]將地下水經濟管理與地下水模擬模型結合,運用動態耦合經濟-地下水模型對地下水開采規律進行不確定性分析.Arnold等[5]將模型參數不確定性考慮到核素運移模擬中,對核素運移及吸附時間進行預報.歐陽琦等[6],常振波等[7]考慮污染質運移數值模擬模型中水文地質參數的不確定性,通過分析其不確定性對污染質運移的影響,對研究區遭受污染風險進行分析與預報.Hauser等[8]將潛水含水層地質結構和水文地質參數的不確定性因素考慮到數值模擬模型中,發現兩者共同作用導致了地下水位的不確定性.多數研究均將模型參數不確定性做為研究核心,忽略了邊界條件不確定性的影響.

然而在地下水運移數值模擬的過程中,模擬預報結果的正確與否和邊界條件處理得是否恰當密切相關.在人類活動影響強度日益增大的今天,處理邊界條件時,往往會面臨一些復雜的問題.原因在于邊界處的水流狀況,不僅受到自然因素的影響,而且還受到人類活動的影響,由于這種耦合效應影響,在模擬預測階段,邊界條件具有很大不確定性.所以在建立研究區的數學模擬模型之前,根據研究區水資源開采計劃、補徑排關系等相關資料,對邊界條件做出合理預報,輔助研究者進行更符合實際的地下水污染質運移預測.

針對于地下水溶質運移的不確定性分析,前人多研究參數的不確定性對模擬模型影響,對于邊界條件的不確定并未多加考慮,本文主要研究第一類邊界條件—已知水頭邊界不確定性對污染質運移結果影響.在對已知水頭邊界預報后,將其不確定性與地下水污染質運移預測相結合,運用Monte Carlo方法針對具體算例進行闡明與分析.首先將模擬預報得到的已知水頭邊界(第一類邊界),做為輸入模擬模型的隨機變量,其它參數作為定值,建立模擬模型的替代模型完成Monte Carlo過程,最后將污染風險評估與不確定性分析結果相結合,完成污染風險預警與分析.運用模擬模型的替代模型完成Monte Carlo模擬過程,不但可以克服反復調用模擬模型產生大量計算負荷的弊端,而且能夠以較高的精度刻畫模擬模型的輸出結果.在大量節約計算成本的同時減少研究耗時.

1 研究方法

1.1 研究區概況

本文用一假想例子對此問題進行研究.建立一個東西長 800m,南北寬 600m,含水層厚度為35m 的不規則研究區域,含水層為均質各向同性潛水非穩定流,含水層巖性I區主要為粗砂,II區為粗砂夾中砂.初始水位為26m,水流方向由西北流向東南,在垂向上接受大氣降水補給,多年平均降水量為 616mm,忽略蒸發騰散消耗量.區域內地表平坦,西北側邊界 Г2有一河流,切穿潛水含水層且與其具有較好的水力聯系.東南側邊界 Г4有一湖泊,切穿潛水含水層且與其具有較好的水力聯系.西北側邊界Г2及東南側邊界Г4均可視為給定水頭邊界,與含水層有較好的水力聯系.東北側邊界 Г1,及西南側邊界 Г3均為微透水介質,可視為隔水邊界.研究區可以劃分為兩個參數分區,其相關參數取值見表1:

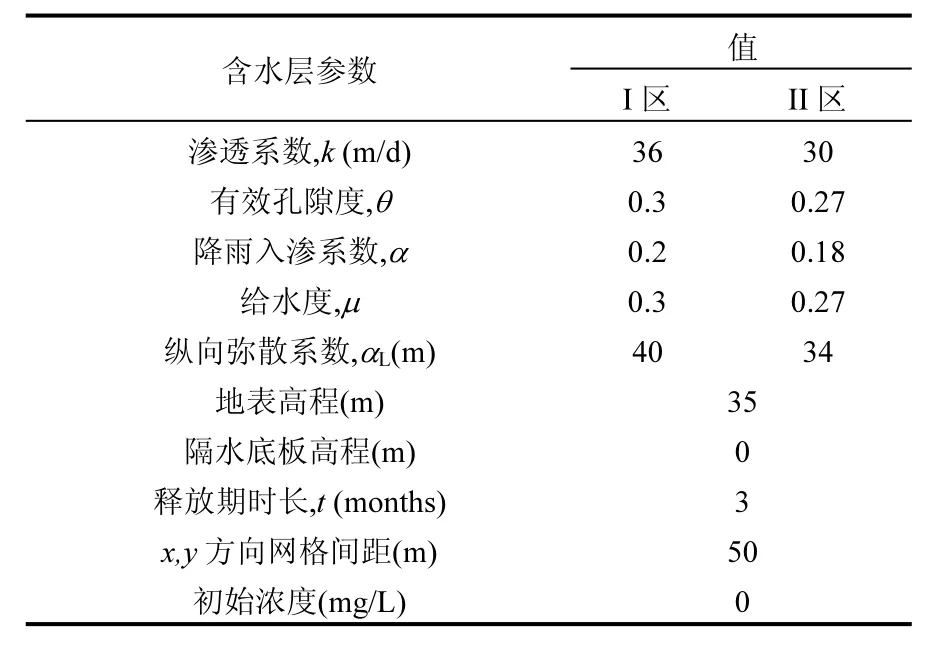
表1 水文地質參數取值Table 1 hydrogeological parameters

研究區內有3口觀測井,編號分別為井1,2,3.區內有一化工廠,因污水池防滲工作出現疏漏,致使污水泄漏到潛水含水層.為預測污染泄露對研究區的影響,建立污染質運移數值模擬模型模擬預測污染質運移,模擬年限為1.5年,每3個月為一個時段,共計 6個模擬時段.污水泄露發生在前 3個釋放時段,污染物釋放強度為1500mg/L,污水泄漏量為 600m3/d.將污染物視為不會發生化學變化及生物轉化與遷移的氯化物.潛水含水層污染物的初始濃度為零,給定水頭邊界 Г2,Г4,隔水邊界 Г1,Г3分別視為零濃度邊界和零通量邊界.研究區污染源觀測井布設位置見圖1.

研究區已知水頭邊界 Г4受人工開采影響比較嚴重,湖泊東南側開采地下水量逐年增長,導致湖泊水位逐年下降.汛期與平枯水期降雨量對湖泊水位也有影響,考慮人工開采影響及降雨徑流影響是十分必要的.所以在預測污染質運移之前,需要對邊界水頭進行預報.

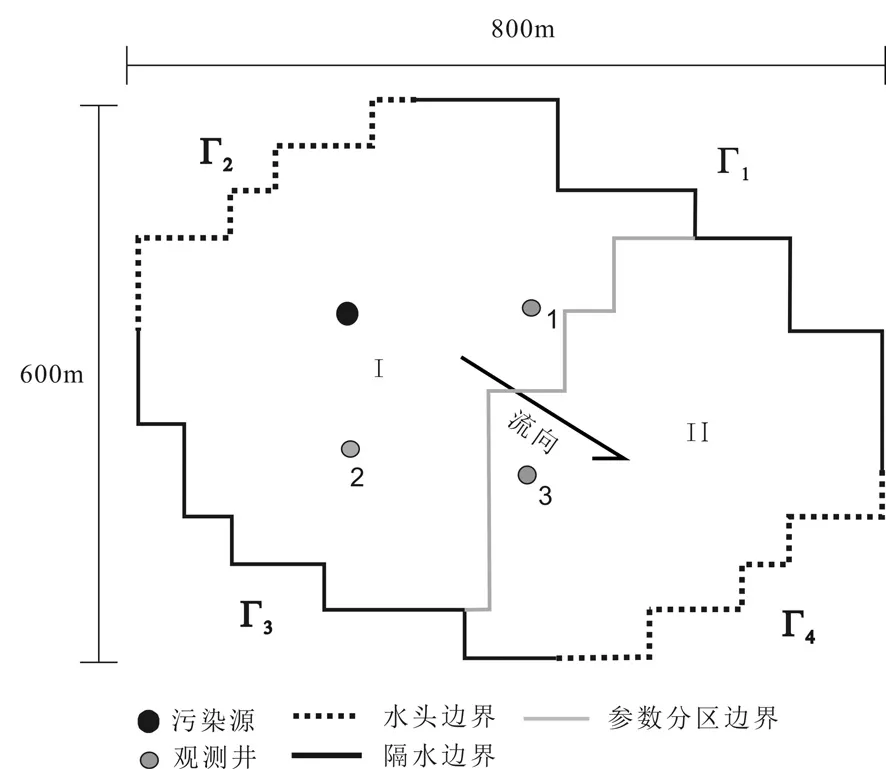
圖1 污染源、觀測井布設位置Fig.1 location of pollution source and observation well

1.2 邊界條件的預報

研究區東南側已知水頭邊界 Г4的東南部約300m 的區域內,建有 5口開采井,開采井的開采量逐年增大(各時段開采量波動范圍見圖2),對研究區東南側邊界的水頭值影響明顯.觀測井各時段的開采量見圖 2,研究區各時段降雨量見圖 3.根據源匯項特征和研究區水文地質條件,運用數值法預報各時段邊界水頭值.各時段預報的邊界水頭值見表2.

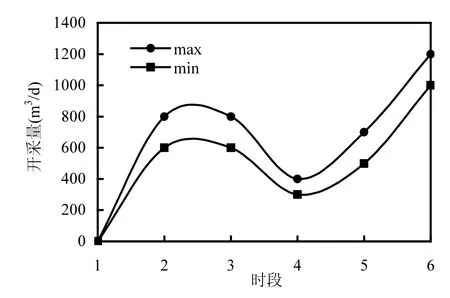
圖2 各時段人工開采量(m3/d)Fig.2 artificial exploitation in different periods (m3/d)

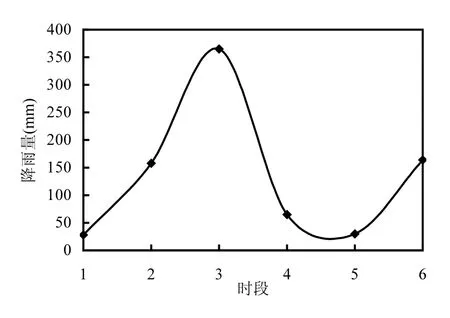
圖3 各時段降雨量(mm)Fig.3 rainfall in different periods (mm)

各時段邊界的水頭值在一定范圍內波動,水頭值在人工開采及自然條件的耦合作用下,呈現出降低的趨勢.

表2 各時段水頭取值范圍Table 2 fluctuation of head value at different periods

下面研究邊界條件-水頭值的大小對于研究區污染質運移的影響.

1.3 污染質運移數值模擬模型的建立

為了對研究區地下水污染質運移進行研究,需要建立地下水污染質運移數值模擬模型,對污染質的運移進行模擬.根據研究區的初始條件與邊界條件,建立地下水水流數值模擬模型:

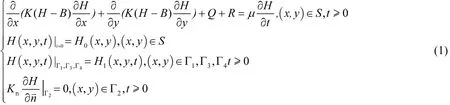
式中:K是含水層滲透系數, m/d;H是潛水水位,m;B是潛水含水層底板高程, m;Q是人工開采強度, m/d;R是降水入滲補給量, m/d;μ是含水層給水度,無量綱;S是模擬區范圍;Г2是定水頭邊界;Г1,Г3,Г4是零流量邊界;Kn是邊界法向量上的滲透系數, m.污染質隨水流運移,在建立好水流數值模型基礎之上,建立地下水污染質運移數值模擬模型:

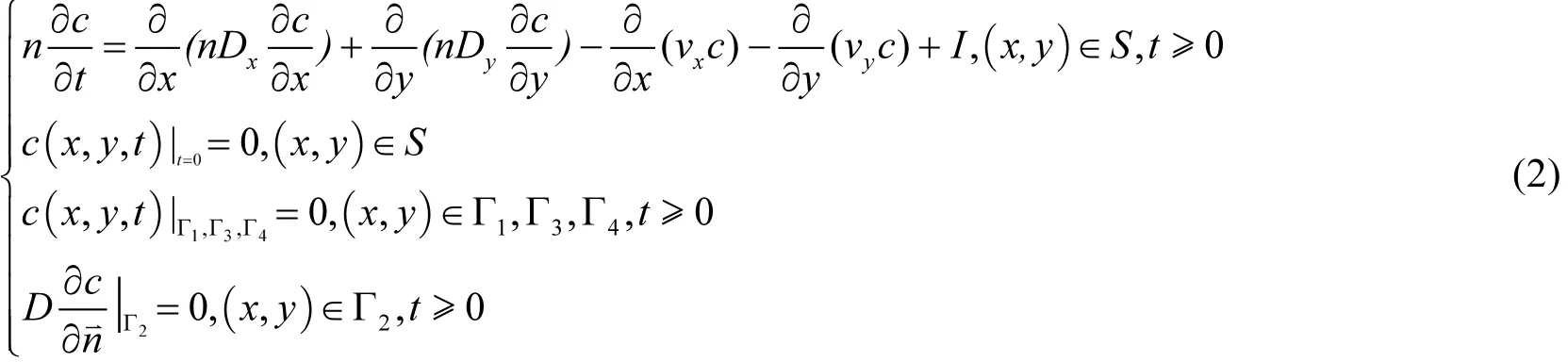
式(2)中:S是模擬區范圍;Г2是定濃度邊界;Г1,Г3,Г4是零彌散通量邊界;n是含水層介質的孔隙度,無量綱;c是污染質濃度,單位 mg/L;Dx,Dy是水動力彌散系數在 x、y方向的分量,單位m2/d;vx,vy為滲透流速v在x、y方向上的分量,單位 m/d. I為單位時間單位液相體積內溶質質量的增減量,mg/(d.m3).

建立的地下水污染質運移模擬模型運用GMS軟件中的Modelflow與MT3D工具箱進行模擬計算.

1.4 替代模型的建立

替代模型是模擬模型輸入輸出響應關系的代替,它不但可以大幅度減少多次調用模擬模型產生的計算負荷,且能夠以較高的精度刻畫出模擬模型輸入輸出數據.本研究中的輸入即是通過邊界條件預報得到的各時段的水頭的取值,輸出則是模型在水頭不同取值情況下運行各時段各觀測井氯化物的濃度值.

本文運用 Kriging方法建立替代模型.Kriging方法是一種基于最小估計方差的無偏估計法,是由南非地質學家Krige[9]提出的一種應用于地質領域的預測方法.目前 Kriging方法廣泛的應用于建立替代模型,運用其原理建立的替代模型不但功能上逼近模擬模型,且調用過程相對簡單,大幅度減少了解決復雜問題的工作量,節省了大量計算成本[10],本文參照替代模型構建的原理與步驟[11-15],運用 MATLAB軟件編寫并調試程序,完成替代模型構建.

首先利用拉丁超立方抽樣方法(LHS)在隨機變量(水頭值)的取值范圍內(表 2)對各時段的水頭值進行抽樣,共抽樣兩大組,第一大組抽樣 45組,第二大組抽樣 10組.將兩大組參數作為輸入值,分別輸入到污染質運移數值模擬模型中,獲得兩大組中各個輸入參數樣本對應的輸出值,兩大組的輸入與輸出值分別構成訓練樣本,檢驗樣本.運用 Kriging方法應用第一大組的訓練樣本建立替代模型.然后應用第二大組的 10 組檢驗樣本對建立的替代模型的精度進行檢驗.替代模型精度檢驗情況見圖 4.由圖 4可知,替代模型運算結果與模擬模型輸出結果,相對誤差均未超過0.01,精度很高,可以代替模擬模型求解.

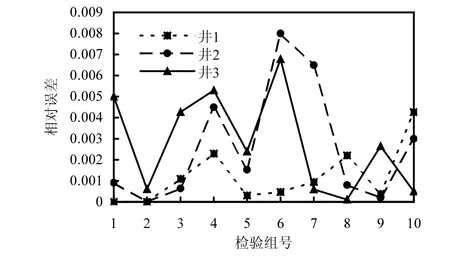
圖4 擬合精度檢驗Fig.4 Fitting accuracy test

1.5 Monte Carlo模擬

Monte Carlo方法是一種概率統計方法, Monte Carlo模擬通常要進行成百上千次的試驗,在模擬過程中認為隨機變量的概率分布函數已知,通過隨機抽樣方法得到多組輸入變量,然后將隨機變量輸入到模型中得到大量的輸出, 每組輸入輸出看做是一次統計試驗,通過對輸出(如地下水中氯化物濃度)的統計可以得到均值,方差等統計估計量,并得到其輸出結果的概率分布情況.

本次研究利用拉丁超立方抽樣法(LHS)對各時段水頭值分別抽樣600組,作為參數樣本,輸入到建立好的替代模型,得到600組響應輸出(即污染物濃度值),然后對這600組響應輸出進行不確定性分析.分別對觀測井1,2,3各時段的污染物濃度值及其遭受污染風險進行統計與分析.

文中運用Monte Carlo方法進行了600次模擬試驗.若 600次試驗都需要調用模擬模型, 每次調用模擬模型計算耗時約 2min,總耗時約1200min.將模擬模型的600次輸入一次輸入到訓練好的替代模型中,替代模型可以在1min內輸出600次輸入對應的輸出,這樣節約了大量人力和時間,減少了不必要計算負荷的產生,又保持了一定的擬合精度.

文中運用的是假想例子,替代模型的優點不是十分明顯,在實際例子中模擬模型運行一次可能需要 1h,甚至更多時間,成百上千次的調用模擬模型,產生的計算負荷之大,耗費的時間之長是難以想象的,這時運用替代模型就可以解決上述問題.

2 結果與討論

本文主要對第 6時段末刻的污染物濃度進行統計分析(實際上各個時段的觀測井污染物風險分析及污染物濃度估計均可以計算,并作為統計分析對象).運用替代模型輸出3口觀測井第6時段末刻的 600組污染物濃度值.利用此數據對觀測井的污染物濃度進行估計,并對觀測井遭受污染風險進行統計與分析.

在統計分析之前,首先討論邊界條件的不確定性對污染物濃度運移的影響.

2.1 對比分析

運用600組污染物濃度數據計算出第6時段末刻污染物濃度最小值與最大值,與邊界條件取定值(數值模擬模型中各個時段中水頭值保持不變)計算得到的污染物濃度進行對比,見表3,對比發現三種情形下 3口觀測井的污染物濃度值相差很大,說明邊界條件的不確定性對污染質運移有較大影響.

在不考慮邊界水頭不確定性的情況下,第 6時段末刻井3中污染物濃度很小,幾乎未被污染.在考慮邊界條件不確定性的情況下,觀測井1、2、3中污染物濃度明顯增大,造成這種結果的原因是人工開采及自然因素的耦合作用使地下水水力梯度變大,地下水流速增大,在相同的時間段內更多的污染質運移到觀測井中,導致觀測井中污染物濃度增大.可見考慮邊界條件不確定性具有重要的實際意義.

表3 污染物濃度對比Table 3 Comparison of pollutant concentration

除了對觀測井內的污染物濃度進行對比,也對研究區第 6時段末刻的污染質運移情況進行對比.圖 5(a)是沒有對邊界條件進行預報,將邊界條件作為定值輸入模型,得到的污染暈分布圖.圖5(b)是對邊界條件進行預報,將各時段邊界條件水頭值作為隨機變量輸入模型,得到的污染暈分布圖.由圖5可知,預測邊界條件,并考慮邊界條件的不確定性對污染質運移情況影響很大,在第 6時段末刻時,兩種情況下的污染暈覆蓋情況有很大差距.(b)圖中,因為水力梯度的增大,污染質運移速度更快,污染暈分布范圍更大.

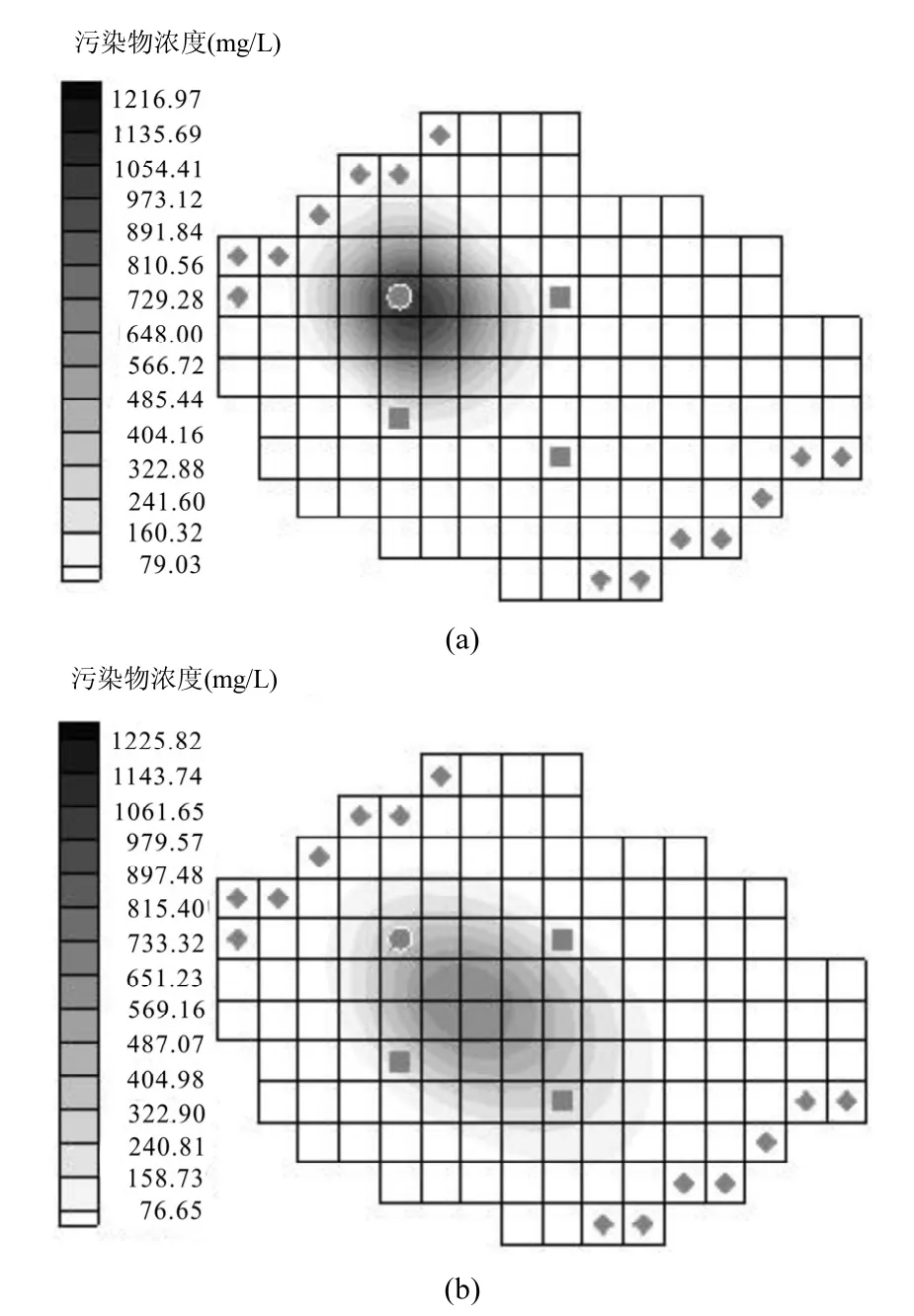
圖5 第6時段末刻污染暈分布情況Fig.5 Distribution of pollution halo at the end of sixth periods

2.2 污染物濃度統計指標分析

運用 600組污染物濃度數據集進行分析,繪制污染物濃度分布直方圖,并對各觀測井污染物濃度值做出統計.結合表3和圖6～8可知,在第6個時段末刻,井2遭受污染程度最嚴重,井1次之,井3遭受污染程度最小,原因是井2與污染源距離較小,最先受到污染,所以遭受污染最嚴重.井3污染物濃度波動最大,可能因為井 3距離邊界條件距離較近,受邊界條件影響明顯.3口觀測井的污染物濃度均值分別為 412.3mg/L、621mg/L、97mg/L.

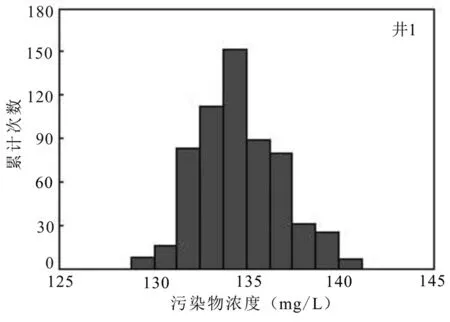
圖6 井1污染物濃度頻數Fig.6 histogram of pollutant concentration frequency for four monitoring periods of well 1

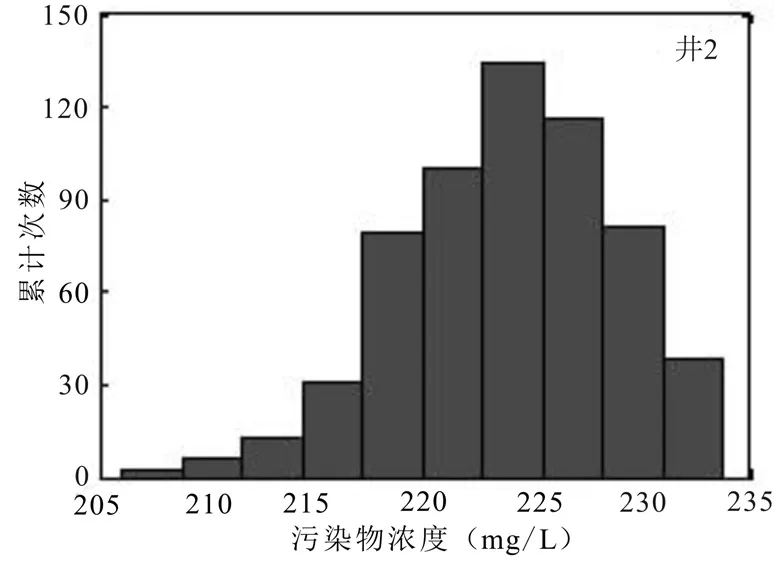
圖7 井2污染物濃度頻數Fig.7 histogram of pollutant concentration frequency for four monitoring periods of well 2

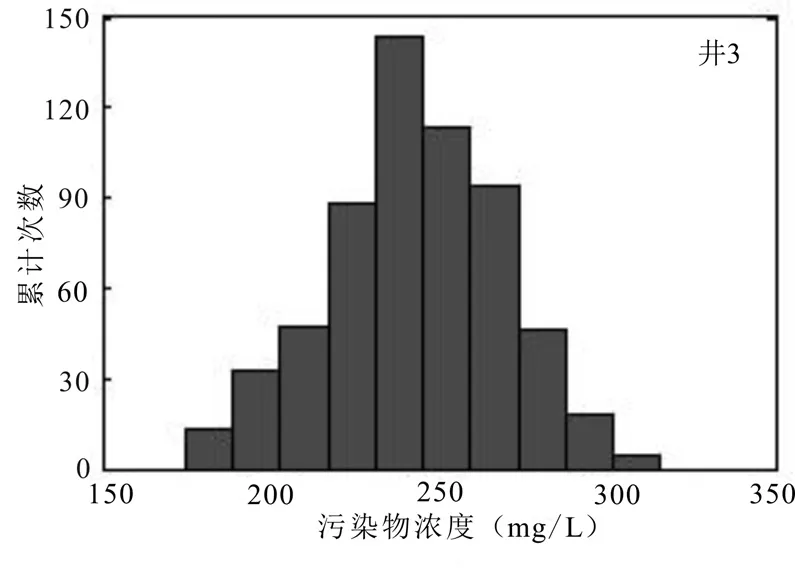
圖8 井3污染物濃度頻數Fig.8 histogram of pollutant concentration frequency for four monitoring periods of well 3

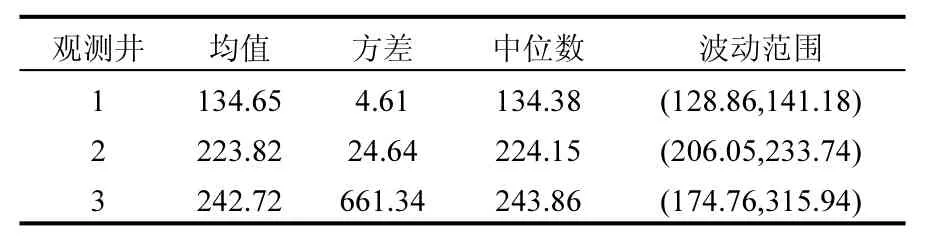
表4 各觀測井污染物輸出值統計指標(mg/L)Table 4 Output statistic indexes of observation wells(mg/L)

2.3 污染物濃度區間估計

相比于確定的輸出,一定置信水平下的污染物取值區間,往往更有借鑒意義,文中運用切比雪夫[16]不等式,對一定置信水平下的觀測井污染物濃度區間進行估計.

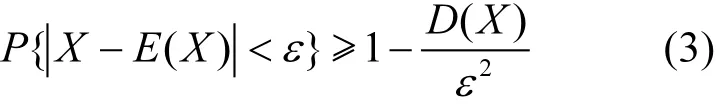
式(3)中:P是置信水平;E(X)是各個時段的觀測井污染物濃度值均值; D(X)是各個時段的觀測井污染物濃度值方差; ε是任意給定正數.利用上式對3口觀測井不同置信水平下的的污染物濃度區間進行估計,見表5.

上表給出了 5口觀測井不同置信水平下的污染物濃度范圍,由表分析知置信水平越低,污染物濃度區間范圍越小;置信水平越高,污染物濃度區間范圍越大.決策者可以規劃需要,選擇相信不同置信水平下的污染物濃度范圍.

表5 不同置信水平井濃度值的區間估計(mg/L)Table 5 interval estimates concentration values of wells with different confidence levels (mg/L)

2.4 污染物超標風險分析

運用輸出數據,參照《地下水質量標準》[17],計算得到第6時段末刻地下水污染物(氯化物)濃度達到I、II、III類水標準的概率,見表6.可以為研究區地下水的合理利用提供參考據.

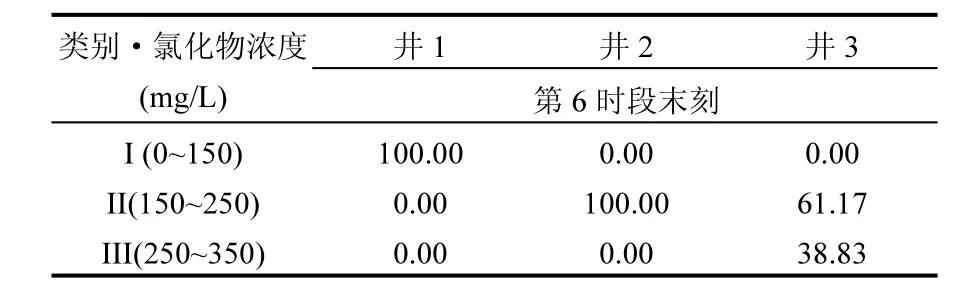
表6 觀測井污染物超標風險分析(%)Table 6 risk statistics of single well pollutant exceeding standard (%)

3 結論

3.1 替代模型是數值模擬模型輸入輸出響應關系的代替,它不但可以大幅度減少多次調用數值模擬模型產生的計算負荷,且能夠以較高的精度刻畫出模擬模型輸入輸出數據,在大量節約計算成本的同時減少研究耗時.

3.2 邊界條件(第一類邊界條件)的不確定性是客觀存在的,而且對于地下水中污染質運移有一定程度的影響.研究地下水污染質運移規律及運移情況時,第一類邊界條件在一定范圍內變化,將其不確定性考慮在內對于污染質運移規律研究是十分必要的.

3.3 通過對 Monte Carlo模擬結果進行統計與分析, 發現考慮與不考慮邊界條件不確定性的研究區污染羽分布差異較大,I、II、III類水所對應的觀測井污染物超標風險不同.應用切比雪夫不等式可以對不同置信水平下的污染物濃度范圍進行估計.

[1]Zeng X K, Wang D, Wu J C. Sensitivity analysis of the probability distribution of groundwater level series based on information entropy [J]. Stoch Env. Res. Risk A, 2012,26:345-356

[2]顧文龍,盧文喜,馬洪云,等.地下水值模擬分析中降水入滲補給強度及滲透系數不確定性評價 [J]. 水電能源科學, 2015,(11):45-48,64.

[3]Jichun W U, Zeng X K. Review of the uncertainty analysis of groundwater numerical simulation [J]. Chinese Science Bulletin,2013,58(25):3044-3052.

[4]Guillaume J H A, Qureshi M E, Jakeman A J. A structured analysis of uncertainty surrounding modeled impacts of groundwater-extraction rules [J]. Hydrogeology Journal, 2012,20(5):915-932.

[5]Arnold B W, Kuzio S P, Robinson B A. Radionuclide transport simulation and uncertainty analyses with the saturated-zone site-scale model at Yucca Mountain, Nevada. [M]// Supplement to the Journal of the Royal Statistical Society. Royal Statistical Society, 2003:1828-1843.

[6]歐陽琦,盧文喜,侯澤宇,等.基于替代模型的地下水溶質運移不確定性分析 [J]. 中國環境科學, 2016,36(4):1119-1124.

[7]常振波,盧文喜,辛欣,等.基于靈敏度分析和替代模型的地下水污染風險評價方法 [J]. 中國環境科學, 2017,37(1):167-173.

[8]Hauser J, Wellmann F, Trefry M. Water Table Uncertainties due to Uncertainties in Structure and Properties of an Unconfined Aquifer. [J]. Groundwater, 2018,56(2):251-255.

[9]Krige D G．A Statistical Approach to Some Mine Valuations and Allied Problems at the Wit—watersrandr [D]. Wilwatersrand:University of Wit-watersrand, 1951.

[10]Luo Jiannan, Lu Wenxi. Comparison of surrogate models with different methods in groundwater remediation pro?cess [J].Journal of Earth System Science, 2014,123(7):1579-1589.

[11]Toal D J J. Some considerations regarding the use of multi-fidelity Kriging in the construction of surrogate models [J].Structural & Multidisciplinary Optimization, 2014,51(6):1223-1245.

[12]Passos F, González-Echevarría R, Roca E, et al. Surrogate modeling and optimization of inductor performances using Kriging functions [C]// Conference: 2015 International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications To Circuit Design., 2015:1-4.

[13]Kwon H, Yi S, Choi S. Numerical investigation for erratic behavior of Kriging surrogate model [J]. Journal of Mechanical Science and Technology, 2014,28(9):3697-3707.

[14]Schmit L A, Farshi B. Some Approximation Concepts for Structural Synthesis [J]. Aiaa Journal, 2015,12(5):692-699.

[15]王曉鋒,席 光,王尚錦.Kriging與響應面方法在氣動優化設計中的應用 [J]. 工程熱物理學報, 2005,26(3):423-425.

[16]Wei-Kai Lai. Rearrangement Inequality and Chebyshev′s Sum Inequality on Positive Tensor Products of Orlicz Sequence Space with Banach Lattice [J]. Journal of Systems Science and Mathematical Sciences, 2014,4(8):574-578.

[17]GB/T 14848-1993 地下水質量標準 [S].