基于分層教學理論的高中雙曲線漸近線的學案設(shè)計

☉內(nèi)蒙古包頭市第四中學 張 輝

高中數(shù)學人教A版選修1-1《雙曲線的簡單幾何性質(zhì)》一節(jié)正文中對雙曲線的漸近線的介紹比較簡單，主要是通過多媒體演示讓學生感受漸近的過程，而該過程的證明實際上在本節(jié)課后的“探究與發(fā)現(xiàn)”部分給出.就近些年高考題來看，對漸近線的考查也僅限于簡單的應(yīng)用，所以很多教師對漸近線的教學也是輕描淡寫、浮于表面，尤其對文科數(shù)學的教學更是如此.筆者認為數(shù)學教學切不可“急功近利”，上課只講考的內(nèi)容，不考內(nèi)容只字不提，那樣數(shù)學課就會變成“識記課”，學生數(shù)學思維的培養(yǎng)也就無從談起.

在受分層教學思想的影響下，本人覺得在講授雙曲線的漸近線內(nèi)容時不僅不能輕描淡寫，還要根據(jù)學生基礎(chǔ)不同，精心設(shè)計出適合各類學生的學案，引導(dǎo)學生通過自己的思考與探索領(lǐng)會雙曲線漸近線的本質(zhì).在學習兄弟學校賈老師的一節(jié)課后，整理出如下學案：

學案A：

（1）函數(shù)y=（k≠0）的圖像是什么圖形？

（2）函數(shù)y=（k≠0）的圖像的漸近線分別是什么？

（3）圖1表示雙曲線C：x2-=1，同學們認為該雙曲線有漸近線嗎？

（4）如果有，請試著畫一畫，猜一猜漸近線方程.

（5）漸近線方程的斜率是什么？斜率與雙曲線方程中的“a，b”有關(guān)系嗎？

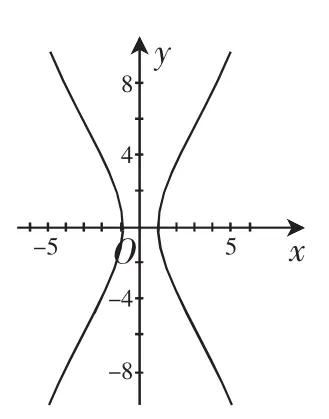
圖1

（6）雙曲線-=1（a＞0，b＞0）的漸近線的方程是______.

（7）請同學們試著說說“漸近線”的“漸近”的表象：______.

（8）當過第一、三象限的漸近線的斜率______時，雙曲線的口越_____；斜率______時，雙曲線的口越______.

（9）等軸雙曲線的漸近線方程為______.

學案B：

（1）函數(shù)y=k x（k≠0）的圖像的漸近線分別是什么？

（2）在圖1中畫一畫雙曲線C：x2-=1的漸近線，并猜一猜方程.

（3）漸近線方程的斜率是什么？斜率與雙曲線方程x2-=1中的“a，b”有關(guān)系嗎？

（4）雙曲線-=1（a＞0，b＞0）的漸近線的方程是______.

（5）請同學們試著說說“漸近線”的“漸近”的表象：______.

（6）當過第一、三象限的漸近線的斜率______時，雙曲線的口越_____；斜率_____時，雙曲線的口越______.

（7）等軸雙曲線的漸近線方程為______.

學案C：

（1）我們學習過反比例函數(shù)的圖像是______其漸近線是______，如何描述其“漸近”特征？

（2）雙曲線C有漸近線嗎？如果有，請畫一畫，猜一猜漸近線方程是______.

（3）你有什么理由認為上述方程是雙曲線的漸近線？

①根據(jù)雙曲線的______性，我們可以將上述問題轉(zhuǎn)化成研究第______象限的問題.

②如何說明第______象限內(nèi)的漸近線與雙曲線的位置關(guān)系？

③用什么數(shù)字特征刻畫“漸近線”的“漸近”特征呢？

④這種數(shù)字特征運算方便嗎？還有相對簡單的數(shù)字特征來刻畫“漸近線”的“漸近”特征嗎？

⑤我們在學習哪部分知識用到了相似的方法？

⑥雙曲線漸近線的斜率變化影響雙曲線什么幾何特征？

這三個學案分別適合基礎(chǔ)在低、中、高層次的學生.雖然都是從學生熟悉的反比例函數(shù)的漸近線入手，一步步引出所要學的雙曲線漸近線的一般性質(zhì).但是，可以看出，學生基礎(chǔ)水平越低，問題設(shè)置越簡單，跨度越小；學生基礎(chǔ)水平越高，問題設(shè)置越難，跨度越大，涉及的內(nèi)容也越深越廣.如此“因材施教”，才能讓學生更輕松卻也更深刻地掌握雙曲線的性質(zhì).在教學過程中，我們要針對不同層次的學生在理解過程中可能遇到的不同問題進行學案設(shè)計，使他們在掌握基礎(chǔ)知識的基礎(chǔ)上得到不同層次的能力提升.

1.人民教育出版社，課程教材研究所，中學數(shù)學課程教材研究開發(fā)中心.普通高中課程標準實驗教科書數(shù)學A版選修1-1數(shù)學［M］.人民教育出版社，2007（2）.

2.翁開鋒.高中數(shù)學分層導(dǎo)學案模式的教學實踐研究.課程教育研究［J］，2017（7）.

3.包水耿.關(guān)于雙曲線的漸近線的若干結(jié)論及其應(yīng)用［J］.中學數(shù)學研究，2002（7）.F