冬小麥雙變量施肥控制策略研究

陳 滿， 施印炎， 汪小旵，3， 孫國祥，3， 魯 偉

(1.南京農業大學工學院，江蘇南京 210031； 2.農業部南京農業機械化研究所，江蘇南京 210014；3.江蘇省現代設施農業技術與裝備工程實驗室，江蘇南京 210031)

過量、不合理的施肥，不僅無法發揮肥料對糧食增產增質的積極促進作用，而且會帶來環境風險，造成土壤板結、污染水源，降低農產品質量[1-2]?，F代農業提倡實施變量施肥技術，結合田間土壤實際肥力以及作物長勢空間差異性，實現小區域按需精準配方施肥，從而降低肥料的投入量、避免肥料的浪費、提高肥料的利用率、降低環境風險，又保障糧食產量和品質[3-4]。

變量施肥技術的實施依賴于先進的變量施肥機械。早期的顆粒肥變量施肥機械多采用單變量控制施肥機構的轉速來實現變量施肥作業控制，這種控制方式簡單，但是調節的范圍較小、精度較低。近些年，在槽輪式變量施肥機械上興起了使用雙變量調節在線控制施肥量，試驗結果表明，雙變量控制調節范圍廣，控制精度高，有利于實現精準變量施肥控制。而雙變量施肥控制策略是該類變量施肥機的核心研究內容，上海交通大學的古玉雪等在這一方面做了相關研究，并應用于測土配方施肥機[5-6]。而基于光譜技術冬小麥變量施肥方面的研究鮮有所聞，因此本研究針對自行研制的基于光譜探測技術的冬小麥變量追肥機械，探討研究其雙變量控制策略，實現變量施肥機雙變量優化控制。

1 變量施肥機雙變量調節機構

本研究的變量施肥機能夠通過控制外槽輪式排肥器的轉速和有效作業開度來實現排肥量實時在線調節，其雙變量調節機構示意圖如圖1所示。外槽輪式排肥器的轉速調節是通過PWM技術控制直流電動機運轉來實現的，直流電動機經減速器由聯軸器直接與施肥機的排肥軸相連接，當直流電動機的轉速發生變化時，排肥器的轉速也將隨之改變，從而改變排肥器的實時排肥量。而外槽輪式排肥器的開度調節則是通過控制步進電動機驅動絲桿滑軌運動來實現的，步進電動機經減速器通過聯軸器與絲桿滑軌相連接，絲桿滑軌上的滑塊經杠桿裝置與施肥機的排肥軸相連接，當步進電動機處于工作狀態時，傳動螺母將沿導軌左右移動，從而帶動傳動軸相應移動，改變排肥器的有效作業開度，由此改變排肥器的實時排肥量。

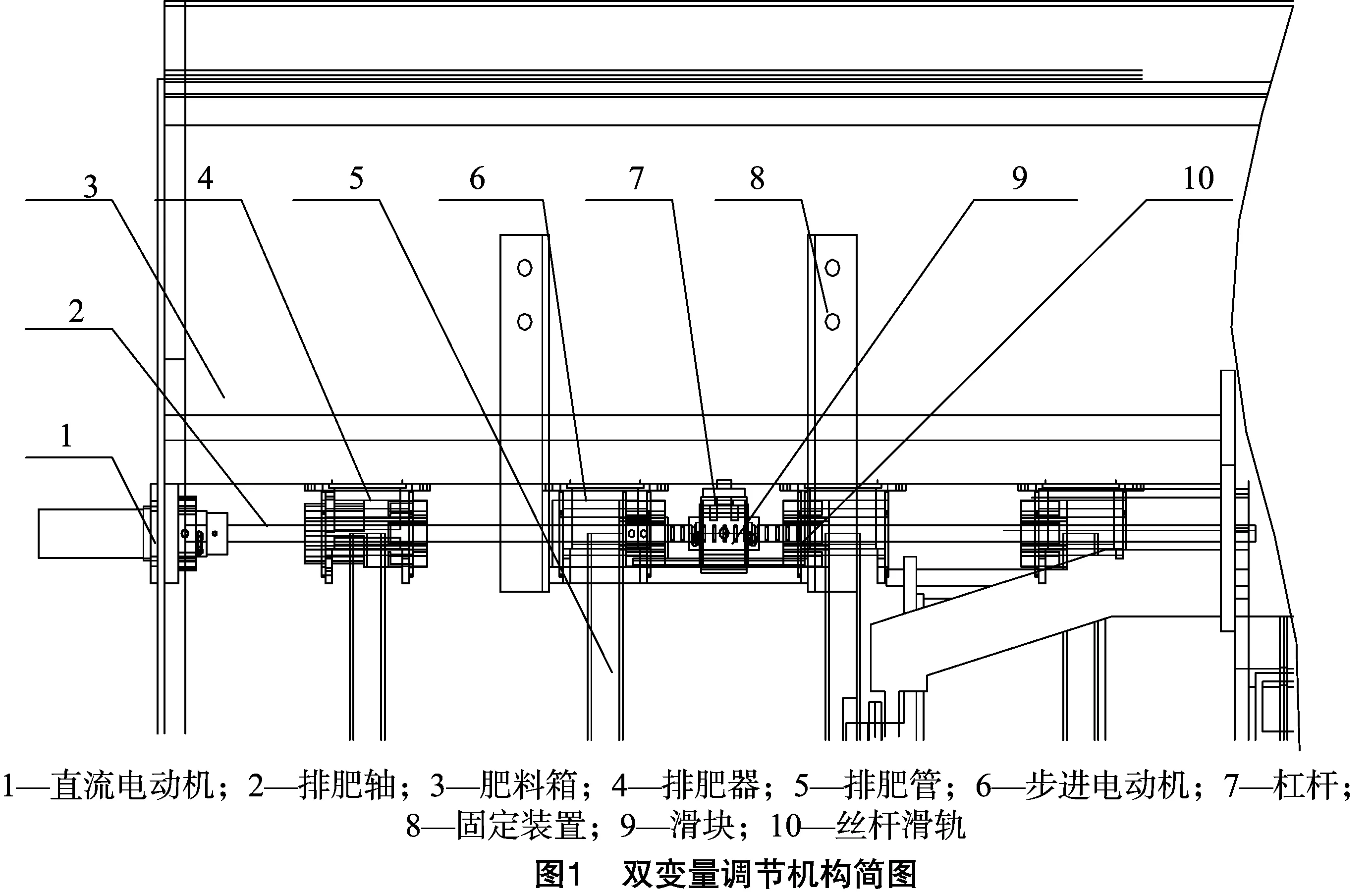
2 排肥器控制模型

2.1 排肥原理

根據耿向宇等的研究，外槽輪式排肥器1 min排肥量可以表示為

(1)

式中：qw為外槽輪式排肥器1 min排肥量，g/min；dw為外槽輪的直徑，cm；lw為外槽輪的有效軸向長度，cm；nw為排肥器實時轉速，r/min；γ為肥箱內肥料容重，g/cm3；aw為肥料對外槽輪凹槽的充滿系數；fw為外槽輪每個凹槽的端面積，cm2；tw為外槽輪的槽節距，cm；cwn為外槽輪帶動層特性系數，cm。其中，除了aw和cwn2個參數隨著外槽輪轉速改變而改變，其他參數均為固定值。然而在實際工作過程中，aw和cwn這2個參數與外槽輪式排肥器轉速之間的關系很難確定，因此借鑒吉林大學和上海交通大學變量施肥機變量施肥控制方面的研究成果[9-10]，通過試驗標定以及數學建模的方式確定排肥量與外槽輪的有效軸向長度以及轉速之間的對應關系。

2.2 排肥量模型

通過排肥器排量的標定獲得排肥器排肥量相關的離散數據，那么便可以通過數學建模的方法獲得排肥器的控制模型，為了避免建模過程中因對試驗數據中突變值的簡單剔除而導致模型丟失重要的隱藏信息，本研究采用Bisquare估計對試驗數據進行穩健回歸分析，建立控制模型。

Bisquare估計是穩健回歸中一種較為常用的M估計(maximum likelihood type estimates)[11-12]。如若自變量y受n個自變量x1，x2，…，xn的影響，又存在線性關系，通過m組觀測值，得到一組數據為(yi；xi1，xi2，…，xin)，i=1，2，…，m，設其對應的線性數學模型：

(2)

式中：β0，β1，β2，…，βn為待定參數；ei為誤差。

M估計就是使目標函數：

(3)

達到最小的β值。

而Bisquare估計的目標函數為

(4)

相應的權重函數為

(5)

通過穩健分析可得系統各個排肥器排肥量所對應的數學模型為

(6)

(7)

(8)

(9)

式中：q1、q2、q3、q4為對控制單元內4個排肥器獨立穩健回歸得到的各排肥器的控制模型，g/s。

各模型曲線擬合結果如表1所示，各模型與測量數據的相關系數均在0.99以上，標準誤差低于0.85。由此可見，穩健回歸得到的排肥器排量模型可以很好地表征排肥性能。

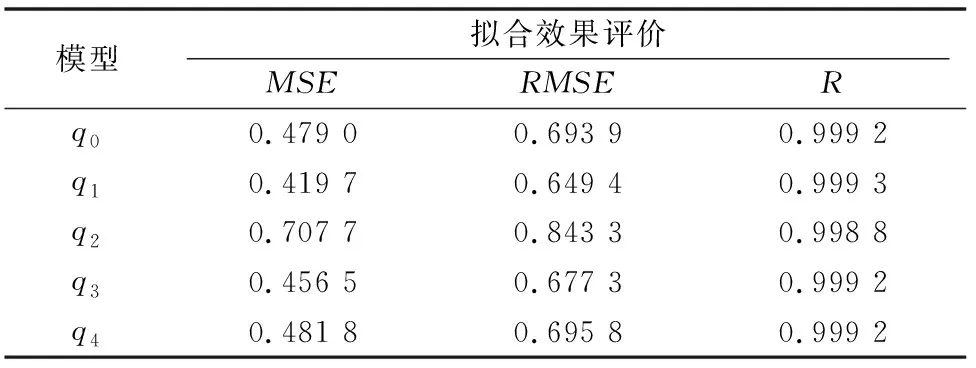
表1 各模型曲線擬合效果

2.3 控制模型

通過Bisquare估計穩健回歸的方法，可以得到各個排肥器排肥量模型。為了實現精確變量施肥，提高系統的控制精度，分析單個排肥器排量模型加權平均建模和排肥器標定數據均值建模2種方式構建排肥控制模型性能的優劣性，從而確定最終的控制模型。

(10)

(11)

式中：q0為對控制單元內排肥器排肥量均值回歸分析得到的排肥量控制模型，g/s；q′為對控制單元內單個排肥器回歸模型加權平均得到的排肥量控制模型，g/s。

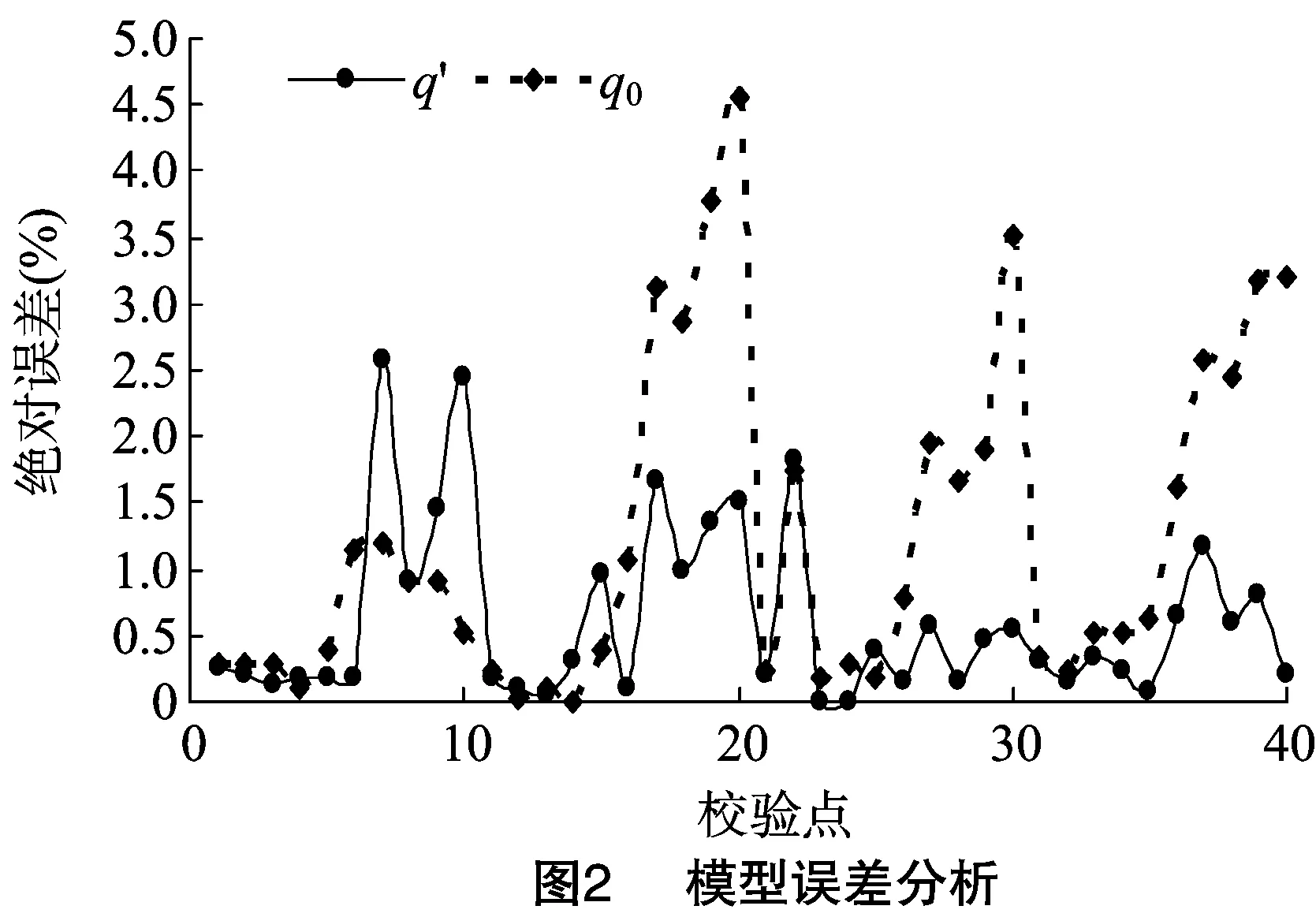
隨機選擇排量標定試驗中獲得的數據對式(10)和式(11)進行驗證分析，結果如圖2所示。試驗結果表明，模型q0的計算值與真實測量值的絕對誤差的最大值為4.55，最小值為 0.01，均值為1.25，標準偏差為1.23；模型q′的計算值與真實測量值的絕對誤差的最大值為2.59，最小值為0，均值為 0.62，標準偏差為0.65。由此可見，模型q′的性能略優于模型q0。因此，本研究選擇模型q′作為系統排肥器的控制模型。

如果忽略施肥機其他機械、作業環境等因素的影響，那么施肥機單個控制系統1 hm2的施肥量：

(12)

式中：Q′為變量施肥機1 hm2的施肥量，kg/hm2；lw為外槽輪的有效軸向長度(有效作業長度)，取值范圍10～40 cm；nw為外槽輪式排肥器實時轉速，取值范圍10～60 r/min；v為變量施肥機的行進速度，m/s。

3 雙變量控制策略

變量施肥機通過光譜監測系統獲取冬小麥冠層的歸一化植被指數，運行變量施肥得到實時的目標施肥量，理論上存在多組不同的轉速和開度組合滿足該目標施肥量調節要求。但是并不是所有組合都適合，例如當前后2次作業開度調節范圍較大時，開度執行機構的響應延時會影響施肥效果；而低轉速高開度的情況下，外槽輪式排肥器會出現堵塞現象。因此，雙變量控制策略對變量施肥系統實施至關重要。本研究分別研究了轉速優先控制、開度優先控制以及轉速開度自適應控制3種控制策略，以期實現變量施肥系統精確控制。

3.1 轉速優先控制

變量施肥機排肥器轉速調節是通過直流電動機無極調速來實現的。轉速優先控制策略實際上就是排肥器開度保持固定值不變，采用轉速單變量調節的方式實現變量施肥。那么就要通過分析各個開度、排肥器不同轉速下，施肥機排肥量的變異性，確定最佳的開度。

圖3是各個開度下排肥器排肥量變異系數的統計結果。統計結果表明，在不同開度下，變量施肥機變異系數的最大值為22.65，變量系數均值的最大值為7.11，最小值為0.74，變異系數的方差最大值為3.31，最小值為0.28。綜合考慮施肥機變量系數的均值、最大值以及方差發現，當排肥器的有效作業開度選擇為18.17 mm時，施肥機施肥量變異系數的方差存在最小值(0.28)，變異系數最大值在所有開度中最小，僅為1.94，而此時的變異系數的均值為1.18，也僅大于所有均值最小值0.44。由此可見，排肥器在該開度下具有最優的排肥性能，因此在轉速優先控制下，排肥器開度保持18.17 mm不變。

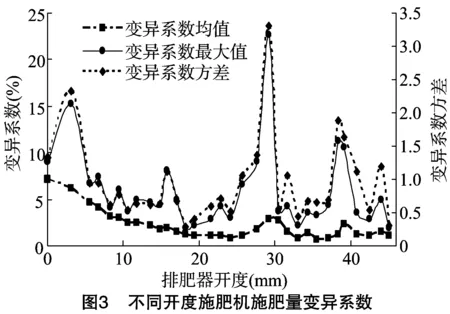
3.2 開度優先控制

類似于轉速優先控制，實際上就是保持轉速為固定值，采用開度單變量調節的方式實現變量施肥調節。因此需要通過分析各個轉速、排肥器不同開度下，施肥機排肥量的變異性，確定最佳的轉速。

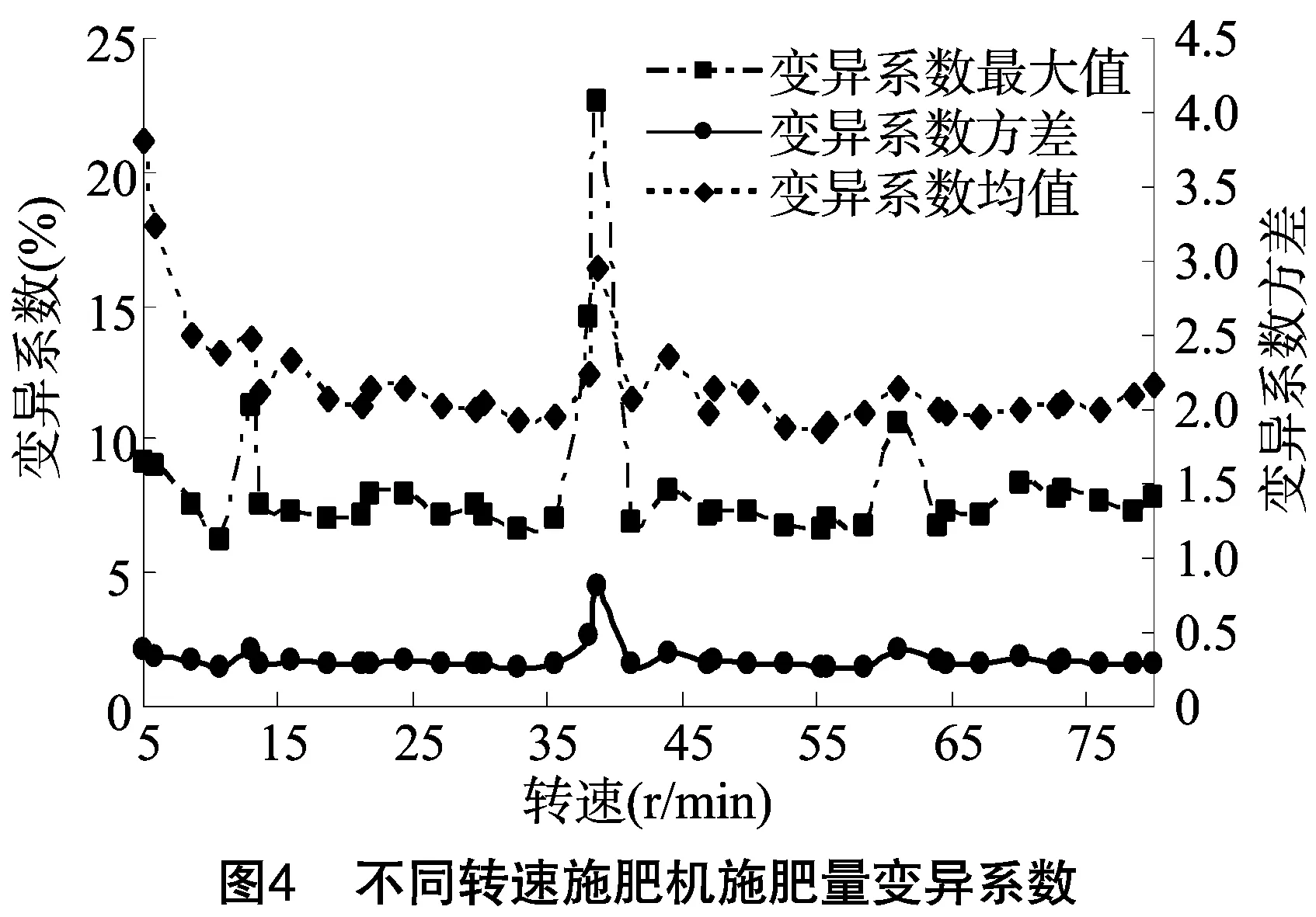
圖4表明，在不同轉速下，變量施肥機變異系數的最大值為22.66，變量系數均值的最大值為3.82，最小值為1.85，變異系數的方差最大值為4.48，最小值為1.42。對比圖3可知，相比于固定開度、調節轉速，在固定轉速、調節開度的情況下排肥器的排肥性能變異系數較大，但是相對穩定性更高，方差波動范圍小。綜合考慮施肥機變量系數的均值、最大值以及方差發現，當排肥器的工作轉速選擇為55 r/min時，施肥機施肥量變異系數的均值存在最小值(1.85)；變異系數最大值為6.64，也僅大于所有轉速下變異系數最小值0.19；變異系數的方差為1.50，也僅大于所有轉速下變異系數最小值0.08。由此可見，排肥器在該轉速下具有最優的排肥性能，因此在開度優先控制下，排肥器轉速保持55 r/min不變。

3.3 轉速開度自適應控制

雖然本研究研制的變量施肥機可以單獨通過調節排肥器的轉速或有效作業開度來實現施肥量的調節。但是，單變量調節存在局限性：僅靠轉速調節時，若電動機轉速發生聚降，會導致排肥器驅動堵塞；而僅靠開度調節時，開度調節機構執行響應時間又是不可忽略的因素，當開度發生聚變時，開度響應延時并將影響施肥效果。而雙變量調節可以很好地兼顧這2方面，避免單因素調節的局限性，從而實現精準變量施肥。根據本研究探討的變量施肥特性，擬建立變量施肥開度轉速查詢表，施肥作業時通過查表法獲得實時轉速開度組合，從而滿足施肥精度和實時性的雙重要求。

借鑒Basso等的研究成果，確定變量施肥系統外槽輪排肥器施肥調節間隔為15 g/s[13-15]，施肥查詢表設置了10個施肥區間A0～A9，分別為0、0～15、15～30、30～45、45～60、60～75、75～90、90～105、105～120、120～∞ g/s。同時借鑒上海交通大學在變量施肥控制序列方面的研究[5-6，10]，制定施肥查詢表內對應的控制量的最佳組合確定原則，并將其描述為一個多元非線性問題的優化問題：

minK=aΔL2+bΔN2+cD+dJ；

(13)

s.t.Lnow∈[10，40]；

(14)

Lnext∈[10，40]；

(15)

Nnow∈[10，60]；

(16)

Nnext∈[10，60]；

(17)

Lnext∈[Lnow-10，Lnow+10]；

(18)

q′(Lnext，Nnext)∈[qdown，qup]；

(19)

ΔL=Lnext-Lnow；

(20)

ΔN=Nnext-Nnow；

(21)

(22)

(23)

式中：Lnow、Lnext為前后2次排肥器的開度，mm；Nnow、Nnext為前后2次排肥器的轉速，r/min；D為排肥器排肥量的變異系數；J為排肥器開度與轉速驟變系數；a、b、c、d、e、f為0～1之間的常數。

利用以上規則，由表2可知，變量施肥控制系統在實際作業時，在獲得冬小麥冠層歸一化植被指數通過決策系統得到目標施肥量后，根據施肥機行駛速度的反饋量，可以逆向求解得到排肥器排肥的均值，然后直接查找查詢表，便可以得到排肥器的目標轉速和開度，系統不需要進行復雜的計算，時效性高，從而更好地實現精準變量施肥。

4 田間試驗

在江蘇省鹽城市響水縣大有鎮黃海農場進行相關田間試驗，變量施肥試驗時變量施肥系統控制策略選擇轉速開度自適應調節，在獲得目標施肥量后，通過查表獲得目標轉速和開度的控制量，再利用模糊PID控制算法實現轉速和開度的在線自適應調節，從而實時地調整施肥量，達到精準變量施肥的目標?，F對其中一組變量施肥試驗結果進行分析，試驗記錄數據包括小麥冠層歸一化植被指數、施肥機實時速率、目標施肥量、目標轉速、目標開度、實時轉速以及實時開度。系統的采樣周期為1 s，部分試驗數據如表3所示。結果表明，變量施肥算法通過查表法可以快速地獲得目標轉速和開度的控制量，并將其作為輸入量輸入模糊PID控制器中，運行模糊PID控制算法，從而實現冬小麥變量精準變量施肥，其中轉速控制誤差低于12.83%，平均誤差小于9.84%；開度控制誤差低于13.57%，平均誤差小于9.34%。由此可見，系統的控制性能良好，可以滿足精準農業變量施肥的技術要求。

5 結論

本研究分析了外槽輪式排肥器的排肥原理，試驗標定了變量施肥排肥器在不同轉速開度下的排肥量，采用Bisquare估計穩健回歸的方法獲得排肥器排肥量模型。各模型與實際測量數據的相關系數均在0.99以上，標準誤差低于0.85。由此可見，穩健回歸得到的排肥器排量模型能夠很好地表征排肥器的排肥性能。

為了獲得可靠穩健的控制模型，本研究分析比較了排肥器排量模型均值建模與排肥器排肥量均值建模的優劣性，試驗結果證明，通過前者獲得的控制模型性能優于后者，因此系統通過對變量施肥控制單元內排肥器排量模型進行加權平均得到最終的控制模型。

本研究分析了雙變量控制策略，確定了在轉速優先控制下排肥器的開度應固定在18.17 mm不變，在開度優先控制下排肥器的轉速應該保持55 r/min不變；為了實現變量施肥轉速開度自適應調節，制定相關規則，建立了最優轉速開度組合查詢表。試驗結果表明，變量施肥控制系統通過查表能夠快速獲得目標控制量，再結合模糊PID控制算法實現排肥量在線自適應調節，變量施肥控制精度達到87%以上。

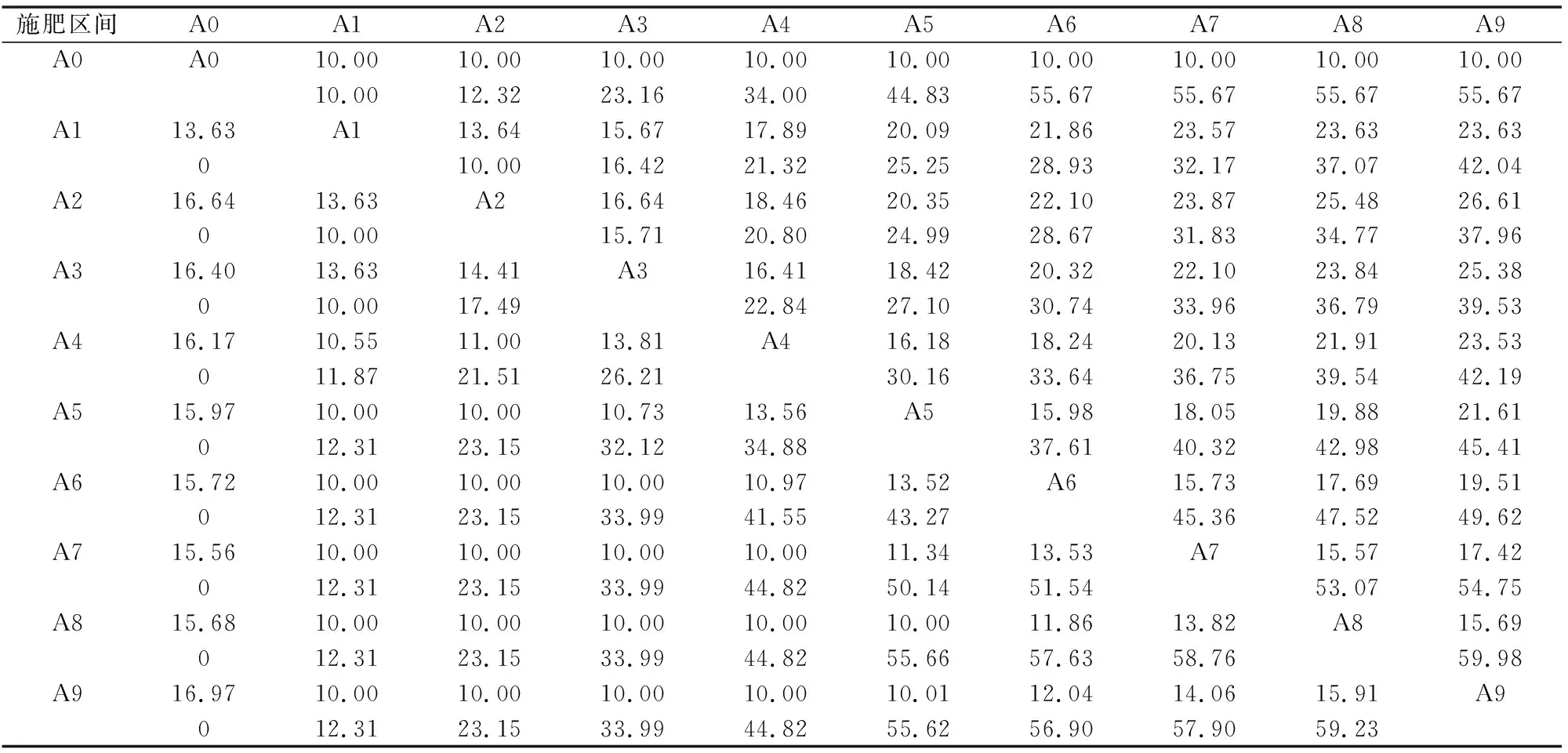
表2 變量施肥開度、轉速查詢

注：每一施肥區間第1行數據為開度，mm；第2行數據為轉速，r/min。

表3 大田試驗結果

參考文獻：

[1]Raun W R，Soil J B，Stone M L，et al. Optical sensor-based algorithm for crop nitrogen fertilization[J]. Communications in Soil Science and Plant Analysis，2005，36(19/20)：2759-2781.

[2]Aguilera E，Lassaletta L，Sanz-Cobena A，et al. The potential of organic fertilizers and water management to reduce N2O emissions in Mediterranean climate cropping systems：a review[J]. Agriculture，Ecosystems & Environment，2013，164：32-52.

[3]Kim Y J，Kim H J，Ryu K H，et al. Fertiliser application performance of a variable-rate pneumatic granular applicator for rice production[J]. Biosystems Engineering，2008，100(4)：498-510.

[4]Papadopoulos A，Kalivas D，Hatzichristos T. Decision support system for nitrogen fertilization using fuzzy theory[J]. Computers and Electronics in Agriculture，2011，78(2)：130-139.

[5]古玉雪，苑 進，劉成良. 基于模糊系統的開度轉速雙變量施肥控制序列生成方法[J]. 農業工程學報，2011，27(11)：134-139.

[6]苑 進，劉成良，古玉雪，等. 基于相關向量機的雙變量施肥控制序列優化[J]. 農業機械學報，2011，42(增刊1)：184-189，171.

[7]耿項宇. 基于GPS/GPRS的變量施肥機控制系統研究[D]. 上海：上海交通大學，2007：43-48.

[8]張 睿. 智能型變量施肥關鍵技術研究[D]. 北京：中國農業科學院，2012：11-15.

[9]張書慧，馬成林，杜巧玲，等. 精確農業自動變量施肥機控制系統設計與實現[J]. 農業工程學報，2004，20(1)：113-116.

[10]古玉雪. 雙變量施肥播種機控制系統研究[D]. 上海：上海交通大學，2012：55-66.

[11]賈潤達，劉俊豪，毛志忠，等. 基于魯棒M估計的間歇過程離群點檢測[J]. 儀器儀表學報，2013，34(8)：1726-1731.

[12]仝海波，張國柱. 改進M估計的抗多個粗差定位解算方法[J]. 測繪學報，2014，43(4)：366-371.

[13]Basso B，Ritchie J T，Cammarano D，et al. A strategic and tactical management approach to select optimal N fertilizer rates for wheat in a spatially variable field[J]. European Journal of Agronomy，2011，35(4)：215-222.

[14]Maleki M R，Ramon H，de Baerdemaeker J，et al. Study on the time response of a soil sensor-based variable rate granular fertiliser applicator[J]. Biosystems Engineering，2008，100(2)：160-166.

[15]Maleki M R，Mouazen A M，Ramon H，et al. Optimisation of soil VIS-NIR sensor-based variable rate application system of soil phosphorus[J]. Soil and Tillage Research，2007，94(1)：239-250.