基于核心素養下的數學變式教學

◎譚雪梅

變式教學— —作為中學數學教學中使用普遍、效果顯著的教學方法，可以建造“模仿”通至“創新”的橋梁。正如建構主義的教育觀點：學習是學習者主動的建構活動，而不是對知識的被動接受，教師僅僅是“助產士”的身份，學生才是教學過程的主體。變式教學正是教師為學生發展搭建的“腳手架”，能夠讓學生的思維經歷產生、發展、形成、遷移的過程，讓學生的探究能力能夠在堅實的基礎之上得到持續性的發展。

重視數學基礎知識和基本技能（雙基）是中國數學教育的優良傳統。重視基礎是為了發展，沒有發展的基礎，恰如花崗巖的基礎上蓋了茅草房。從“雙基”到“三維目標”的發展歷程，已經為中國的教育發展打下了堅實的基礎，而“核心素養”正是在此基礎之上中國教育謀求發展的必由之路，“變式教學”正是這條發展道路上高速便捷的交通工具。

通過對數學問題進行多角度、多方面的變式探索研究，有意識地引導學生從“變”的現象中發現“不變”的本質，從“不變”的本質中探索“變”的規律，從而優化學生思維品質，培養和提升學生的數學核心素養。

一、引入變式教學，把握數學概念

概念的掌握是數學學習的前提和基礎，只有在充分掌握數學概念的前提下，數學知識的導入才能成為可能。反觀初中生對數學概念的認識，我們發現不少學生容易陷入本質屬性泛化的誤區。初中生抽象思維能力和邏輯思維能力有限，有時受到許多無關特征的干擾，僅僅從概念的表層特征認識事物，對于概念的本質屬性認識不到位。由于從一開始就沒有對數學對象形成清晰完整的認識，此后一系列的數學認識活動便陷入了惡性循環。數學概念反映了事物的共同點，但是很多時候，事物不僅在本質特征方面具有共同點，在非本質特征方面也具有共同點。為了讓學生真正掌握一個概念，教師不但要從共同本質屬性角度切入進行教學，而且還要注意通過正反變式，讓學生學會如何排除非本質屬性。

例如，二次函數概念教學中，很多學生通過一般解析式y＝ax2+bx+c初步認識二次函數概念之后，教師還要用變式加深學生對二次函數本質屬性的認識。通過一般式與頂點式及交點式的對比，學生在多次選擇、判斷、篩選過程中，慢慢就能明白哪些是二次函數的本質屬性，哪些是非本質屬性。

變式1：y＝ax2+k

變式2：y＝a（x-h）2

變式3：y＝a（x-h）2+k

變式4：y＝a（x-x1）（x-x2）

二、習題變式教學，促進知識遷移

習題是初中數學教學不可或缺的一部分，但也是常讓學生深感頭痛的一部分內容。很多學生自以為將教材上面的概念、定義、公式、原理掌握得差不多了，可是遇到習題還是無處下手。現代認知心理學的知識分類學習論指出：“程序知識或智慧技能學習一般要經歷三個階段，其發展的最后階段是通過變式訓練來實現操作技能的自動化。”數學知識轉化和應用階段，教師應當加強習題變式訓練，從學生熟悉的、簡單的習題入手，逐漸過渡到較為相似的新穎題目，一步步幫助學生建立解題信心。這樣做，避免了因為解題遇到挫折而喪失學習積極性情況的出現，同時又極大地促進了學生對數學知識的縱向遷移。

例如，原題：“小明站在教室中央，若要小軍與小明的距離為3米，那么小軍應該站在哪里？有幾個位置？請通過畫圖來說明。”這道題目的考查點和圓的位置相關，屬于初級題型，難度較低，在大部分學生力所能及范圍之內。當學生順利解決這個問題之后，教師可以進一步延伸出如下變式：小明站在教室中央，若要求小軍與小明的距離等于3米，小軍與小麗距離2米，那么小軍應該站在哪兒？有幾個位置？通過解決表面相似的問題，學生認知負荷逐漸增加，高層數學思維被喚醒，這對于將原先的基礎知識轉化為策略知識具有重要意義。

三、嘗試一題多解，提高思維能力

正所謂“條條大路通羅馬”，很多數學問題的解決方法不止一個。雖然答案是固定的，但是找到答案的方法卻各式各樣。針對同一個數學問題，教師應該鼓勵學生嘗試一題多解，開動腦筋尋找更多常規思維之外的解題方法。這樣可以幫助學生感悟數學知識之間的共性，不僅有助于培養他們數學思維的深刻性，同時也能進一步激發學生參與數學活動的興趣。在平時的課堂訓練中，教師要注意抓住教育契機，適時開展一題多解訓練，促進學生數學思維能力的提高。

例如，張明買13支鉛筆、5塊橡皮、9個糖果，一共用去9.25元。如果買2支鉛筆、4塊橡皮、3個糖果，則要用去3.2元，請問買鉛筆、橡皮、糖果各一個，需要用去多少元錢？設鉛筆、橡皮、糖果分別為x、y、z，根據題意：

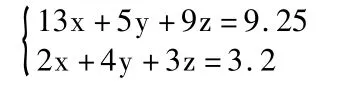
列方程求解時，由于是三元一次方程組，可用解三元一次方程組的方法求得解。但是問題其實并不是分別求x、y、z，而是求x+y+z，因此可以通過湊整法、主元法、消元法、參數法、待定系數法等方法進行解答。這些方法都能巧妙化解原方程組已知量不足的問題，最后可以求出答案為1.05元。

核心素養是作為客體側面的教育內容與作為主體側面的學習者關鍵能力的統一體而表現出來的，因此，核心素養不是先天遺傳，而是經過后天教育習得的。通過教師的恰當引導，善加利用“變式教學”，將教學實踐與核心素養有機的結合在一起，是值得廣大師生共同研究和探討的課題。

［1］王春霞.平常題“非常”運用提升學生核心素養——一道高三模擬試題教學為例［J］.中學數學研究，2017（11）：5-7.

［2］蔡敬發.高職班數學運算核心素養的培養［J］.福建基礎教育研究，2017（04）：57-59.

［3］李重庚.談數學教師的核心素養［J］.湖南教育（C版），2016（08）：37-38.