一個“新”的直線系

江西省樟樹中學 (331200) 萬浩春

(文)16.設直線系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)，對于下列四個命題：

A．存在一個圓與所有的直線相交

B．存在一個圓與所有的直線不相交

C．存在一個圓與所有的直線相切

D．M中的直線所能圍成的三角形面積都相等

其中真命題的代號是 (寫出所有真命題的代號).

(理)16.設直線系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)，對于下列四個命題：

A．M中所有直線均經過一個定點

B．存在定點P不在M中的任意一條直線上

C．對于任意整數n(n≥3)，存在正n邊形，其所有邊均在M中的直線上

D．M中的直線所能圍成的三角形面積都相等

其中真命題的代號是 (寫出所有真命題的代號).

解決這兩道題的關鍵在于讀懂直線系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π)是什么樣的直線系？直線系中的直線擁有什么樣的共同特征？

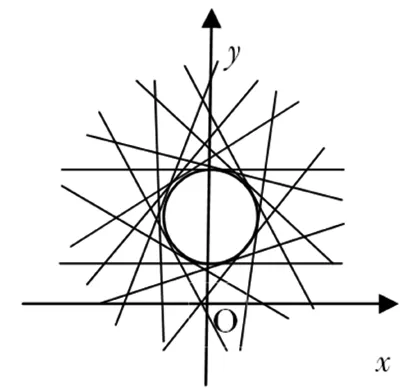
圖1

我們觀察方程xcosθ+(y-2)sinθ=1(0≤θ≤2π)，可以發現定點(0，2)到方程表示的所有直線的距離均為1，那么這個方程表示的直線系就是以(0,2)為圓心，以1為半徑的圓的所有切線組成的直線系.如圖1所示

對于(文)16ABC這三個選項容易判斷均正確，D選項不正確，因為M中的直線所能圍成的三角形并不都是定圓的外切三角形，有時是三角形的邊的延長線和定圓相切.對于(理)16，A顯然不對，B、C正確，D不正確.

這個“新”的直線系不同于我們已經熟知的平行(或垂直)某一直線的直線系，或恒過某一定點的直線系，他是由一個定圓的所有切線組成的直線系.

那么對于任意一個圓，它的所有切線能組成一個直線系嗎？如果能，這個直線系的方程是什么呢？

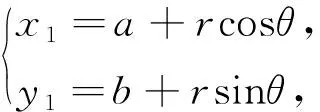
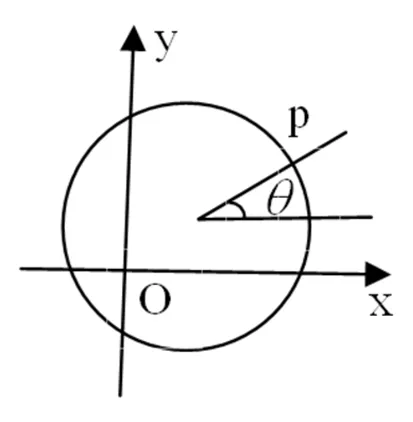
圖2

一般地，圓(x-a)2+(y-b)2=r2的所有切線組成的直線系方程為(x-a)cosθ+(y-b)sinθ=r(0≤θ≤2π).

(特別說明，這個θ就是圓的參數方程中的參數，所以它的幾何意義表示：以圓心為頂點，平行于x軸正方向的直線為始邊，切點與圓心的連線為終邊的角，如圖2.)

利用這個“新”的直線系我們可以比較簡單的解決下列問題

例1l1與l2是直線系M：(x+1)cosθ+(y-2)sinθ=3(0≤θ≤2π)中的兩條平行線，則l1與l2間的距離為( ).

分析：直線系M：指的是以(-1,2)為圓心，3為半徑的圓的所有切線，∵l1∥l2，又都與圓相切，∴l1與l2間的距離就是圓的直徑，故選C.

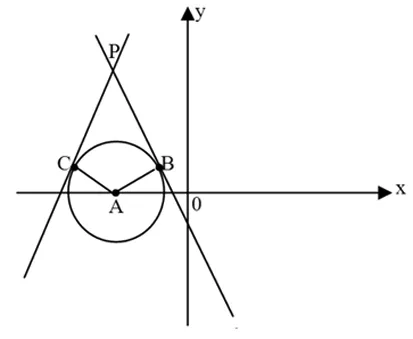
圖3

例2l1：(x+3)cos25°+ysin25°=2,l2：-(x+3)sin55°+ysin35°=2,l1與l2相交于P點，則P到A(-3,0)的距離為 .

例3 在平面直角坐標系中既能用(x-1)cosθ+(y-2)sinθ=1表示又能用(x-3)cosθ+(y-1)sinθ=2表示的直線一共有幾條？

分析：(x-1)cosθ+(y-2)sinθ=1表示以(1，2)為圓心，1為半徑的圓的所有切線組成的直線系,(x-3)cosθ+(y-1)sinθ=2表示以(3，1)為圓心，2為半徑的圓的所有切線組成的直線系.

故這道題的實質是求兩圓(x-1)2+(y-2)2=1和(x-3)2+(y-1)2=4共有多少條公切線.

解：∵圓(x-1)2+(y-2)2=1和(x-3)2+(y-1)2=4相交，所以合題意的直線共有2條.

任意一個圓的所有切線能組成一個直線系，那么一個橢圓的所有切線能否組成一個直線系？這個直線系的方程該如何表示？

我們可以類比圓的切線系方程的推導過程進行推導.

A．存在一個圓與所有的直線相交

B．存在一個圓與所有的直線不相交

C．存在一個圓與所有的直線相切

D．M中所有直線均經過一個定點

E．存在定點P不在M中的任意一條直線上

其中真命題的代號是 (寫出所有真命題的代號).

例5 已知l1：3cos25°x+4sin25°y=12,l2：3sin54°x+4sin54°y=12,若兩條直線交于點P,則點P( ).

A.在圓x2+y2=9的內部

B.在圓x2+y2=9的外部

C.在圓x2+y2=9上

D.無法判斷與圓x2+y2=9的位置關系

封閉圖形圓和橢圓都有切線系，那么另外的兩個圓錐曲線雙曲線和拋物線是不是也有類似切線系？

也就是說，只要把曲線的參數方程代入過曲線上某一點的切線方程，就可以得到曲線的所有切線組成的直線系方程.這為我們以后解決與圓錐曲線的切線有關問題提供了一個全新的思考途徑.