“4E”級寬扁型江海直達船結構安全可靠性探析

裴志勇 朱 波 吳衛國

(武漢理工大學交通學院1) 武漢 430063) (武漢理工大學高性能艦船技術教育部重點實驗室2) 武漢 430063)

0 引 言

船舶大型化是當前航運市場主要趨勢，大型船舶有較高的運輸效率、較低的能源消耗，從而有良好的經濟性，在嚴酷的市場環境中具有競爭優勢[1].但由于長江是自然航道，船長、吃水受限，型深受橋梁凈空高制約，大型化唯有增加船寬，開發適應長江自然條件的寬扁型船舶.

以載量大、油耗低、節能環保、經濟高效為目標開發出武漢-寧波舟山航線“4E”級(節能energy-saving、環保environment-friendly、經濟economy、高效efficient)寬扁型江海直達集裝箱船開發過程中，寬扁船型設計加上貨艙采用長大開口使得其總縱強度較弱，在海段遭遇到惡劣海況時引起船體結構破壞的概率增加.柴俊凱[2]通過改變12 400 t江海直達船關鍵區域的材料屬性與板厚從而進行優化分析，得到了提高船體極限強度的有效途徑.傅何琪[3]提出了一種解析方法用以評估破損狀態下江海通航干貨船的船體縱向構件的損失程度. Nilva等[4]對江海通航集裝箱船在損失部分船體縱向構件下的船體剩余強度進行了分析.Nilva[5]對具有長、大開口的江海直達貨船在彎扭載荷下的極限承載能力進行了分析，探討了復合載荷下船體極限強度隨開口尺寸增大的變化規律，但缺乏對寬扁船型的結構特性研究.

本文從作用于寬扁型江海直達船體的載荷和船體結構極限承載能力兩方面進行計算分析，對開發船的結構安全可靠性進行評估，從而明確船體的安全裕度，使其能安全可靠使用.

1 船體結構極限強度

船體結構極限強度是指其具有的最大承載能力，如果船舶遭受的外載荷比船體結構極限強度大，則會發生船體崩潰，導致海難海損事故發生.因此，極限強度計算是保證船體結構安全可靠的重要內容.

通常計算船體結構極限強度的方法有直接計算法和逐次崩潰分析法.直接計算法是面向設計的方法，包括線彈性方法、經驗公式法以及解析方法等.線彈性方法簡單易用，但結構屈曲后不再保持線性關系，故該法精度不高，僅在設計初期估算極限強度的大致范圍；經驗公式法是由有限的數據推導而來，僅對常規、通用的已有船型有較好的結果；解析方法通過假設船體剖面在極限狀態時的應力分布，考慮屈曲和屈服的影響，用理論方法得出船體梁的極限強度，其計算精度很大程度上取決于假設的極限狀態船體剖面應力分布.逐次崩潰分析法著眼于結構崩潰全過程，可考慮構件失效的先后順序以及極限強度后承載能力的降低，其最大承載能力即為結構的極限強度.逐次崩潰分析法包括簡易方法如Smith法、非線性有限元法(NFEM)[6]和理想結構單元法(ISUM)[7]等.

非線性有限元法可以很好的模擬結構的屈曲/屈服行為，但一般需要較細的網格、較多的單元才能得到合理可靠的結果，對于船體梁這樣的大型結構系統而言，往往由于計算時間過長而無法實際上實施.理想結構單元法是將結構的非線性行為理想化并包括在單元中，這樣可以將較大的幾何單位(如加強筋間的板格)視作一個理想結構單元，從而減少計算工作量；其計算精度很大程度上取決于單元理想化的合理程度.Smith法是將船體剖面離散成板和加筋板單元，考慮極限強度后承載能力的降低和崩潰的先后順序，來揭示彎曲載荷下船體梁的逐次崩潰行為；該方法因簡單易行得以廣泛應用，已經作為標準方法納入了散貨船、油船的共同規范體系，指導上述兩種船型的極限強度校核.

Smith法在進行逐次崩潰分析時，先將剖面離散成各個單元，在端面施加轉角，計算各單元的應變量，由單元應力應變關系可求得相應的應力，再2次積分即可得到相應的彎矩；繼續增加轉角，就會得到一系列彎矩和轉角的關系.將轉角除以橫框架間距即得到相應的曲率，從而得到船體梁的彎矩-曲率關系曲線[8].具體求解步驟如下.

步驟1將船體剖面離散成各個單元，包括板單元、加筋板單元和硬角單元，其中硬角單元由若干相交的板組成，用來模擬不可能發生屈曲的構件，其應力應變關系通常假設為理想彈塑性模型.

步驟2計算所有單元的平均應力-平均應變關系.

步驟3設定初始曲率和初始中和軸位置，一般取使甲板處應力達到其屈服應力的1%時所對應的曲率為初始曲率.

步驟4根據各單元中心離中和軸的距離確定各個單元的應變.

步驟5按照單元的平均應力-平均應變關系，求得各個單元相應的應力.

步驟6對于每一個增量步，以整個剖面的靜力平衡為準則，確定中和軸的位置.

步驟7將各個單元所受的力對中和軸求矩，并將其相加，得到作用在整個剖面的彎矩.

步驟8增大曲率值，轉回步驟4，繼續求解，得到一系列彎矩-曲率關系曲線，其最大值即為船體梁的極限強度.

2 寬扁型江海直達船體結構極限強度

2.1 寬扁型江海直達船結構特點及主尺度

在江海直達船開發過程中，通過開展經濟性分析、適航性能和結構安全性能研究，以裝載量大、油耗低、節能環保、安全高效為目標，開發出寬扁型節能環保江海直達集裝箱船.采用理論分析、數值計算和模型試驗相結合的研究方法，攻克寬扁船型在安全技術、節能技術、綠色技術應用等方面的關鍵技術問題，以達到安全、降耗和環保的目標.

目標船主尺度見表1.采用雙底雙殼結構，雙層底高1.5 m，雙殼寬2.6 m，雙殼間設2層平臺，分別距基線3.8和6.3 m，典型橫剖面見圖1.該船的型寬型深比(B/D)達到了2.98，超出了當前中國船級社海船規范規定的B/D不大于2.5的規定.寬扁型船總縱強度偏弱，給合理、安全、可靠的船體結構設計帶來了巨大挑戰.

表1 寬扁型江海直達船主尺度

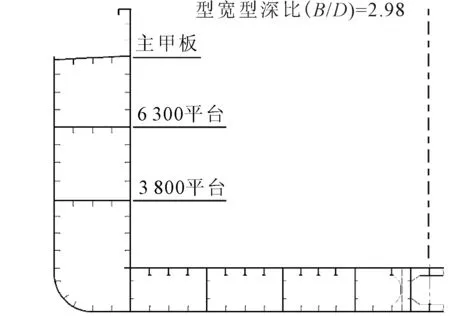
圖1 寬扁型江海直達船典型橫剖面圖

2.2 船體結構逐次崩潰行為

采用基于彈性大變形分析和剛塑性力學分析相結合的半解析方法開發的程序系統“HULLST”用于“4E”級寬扁型江海直達船體結構崩潰行為分析，該程序系統計算分析精度已經在系列對比計算中得以驗證[9-10].計算時，采用“雙跨”模型，即計算模型包括從強橫框架位置出發向前及向后各半個橫框架間距，計算模型的前后端面為兩強橫框架的中間，根據變形特征施加對稱的邊界條件，強橫框架剖面處由于強橫框架的作用，根據變形特征在船底限制垂向平動自由度(Uz=0)及縱向轉動自由度(θx=0)，在舷側限制橫向平動自由度(Uy=0)及縱向轉動自由度(θx=0),見圖2.

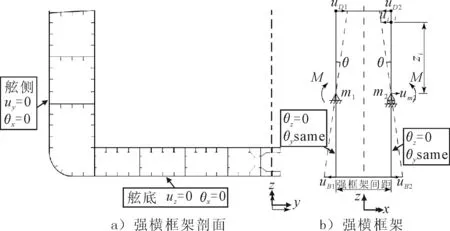
圖2 計算模型及邊界條件

在計算模型的前后端面任意位置設主節點m，基于平斷面假定，斷面上各節點與主節點的橫向轉動自由度(θy)保持一致，主節點有縱向平動自由度(Um)和橫向轉動自由度(θm).距主節點距離Zi的節點i，其位移量與主節點位移量的關系為

di=Hidm

(1)

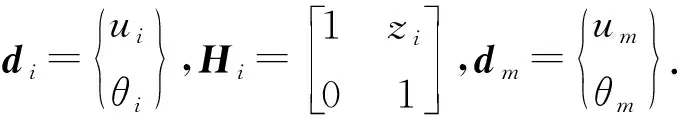
同樣，各節點i處的節點力Fi及彎矩Mi可通過下式轉換為主節點的等效節點載荷：

Fm=HiTFi

(2)

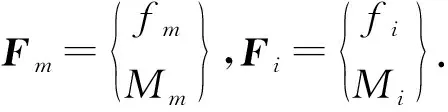
逐步加大主節點處的轉角從而獲得相應的彎矩值，得到彎矩-曲率關系曲線.開發的“4E”級寬扁型江海直達船具有雙底單甲板結構，因而其中垂彎矩較中拱彎矩要小.中垂狀態下船體結構彎矩-曲率關系曲線見圖3.

圖3 中垂狀態船體結構彎矩-曲率關系曲線

不同載荷水平下各構件的應力分布見圖4.圖4中的實心圓為該構件發生了屈曲，三角形為該構件發生了屈服.在加載初始階段，彎矩水平不超過1.0×106kN·m時，船體結構各構件均呈彈性狀態，應力沿高度方向呈線性分布，見圖4a),隨著彎矩的增加，各構件的應力也逐漸增大，甲板結構在縱向壓縮載荷作用下首先發生屈曲，船體結構總體剛度降低,見圖4b)；隨著彎矩的進一步增加，甲板結構、6 300平臺結構以及6 300平臺以上的舷側結構和內殼結構等先后屈曲，中和軸位置向下移動，船底結構部分構件屈服，從而整體結構喪失承載能力，達到極限強度狀態,見圖4c)；上部結構屈曲后各構件的應力會重新分配，中和軸位置進一步向下移動，更多舷側結構和內殼結構發生屈曲，更多船底結構發生屈服，變形增大的同時斷面彎矩急劇降低，典型應力分布,見圖4d).

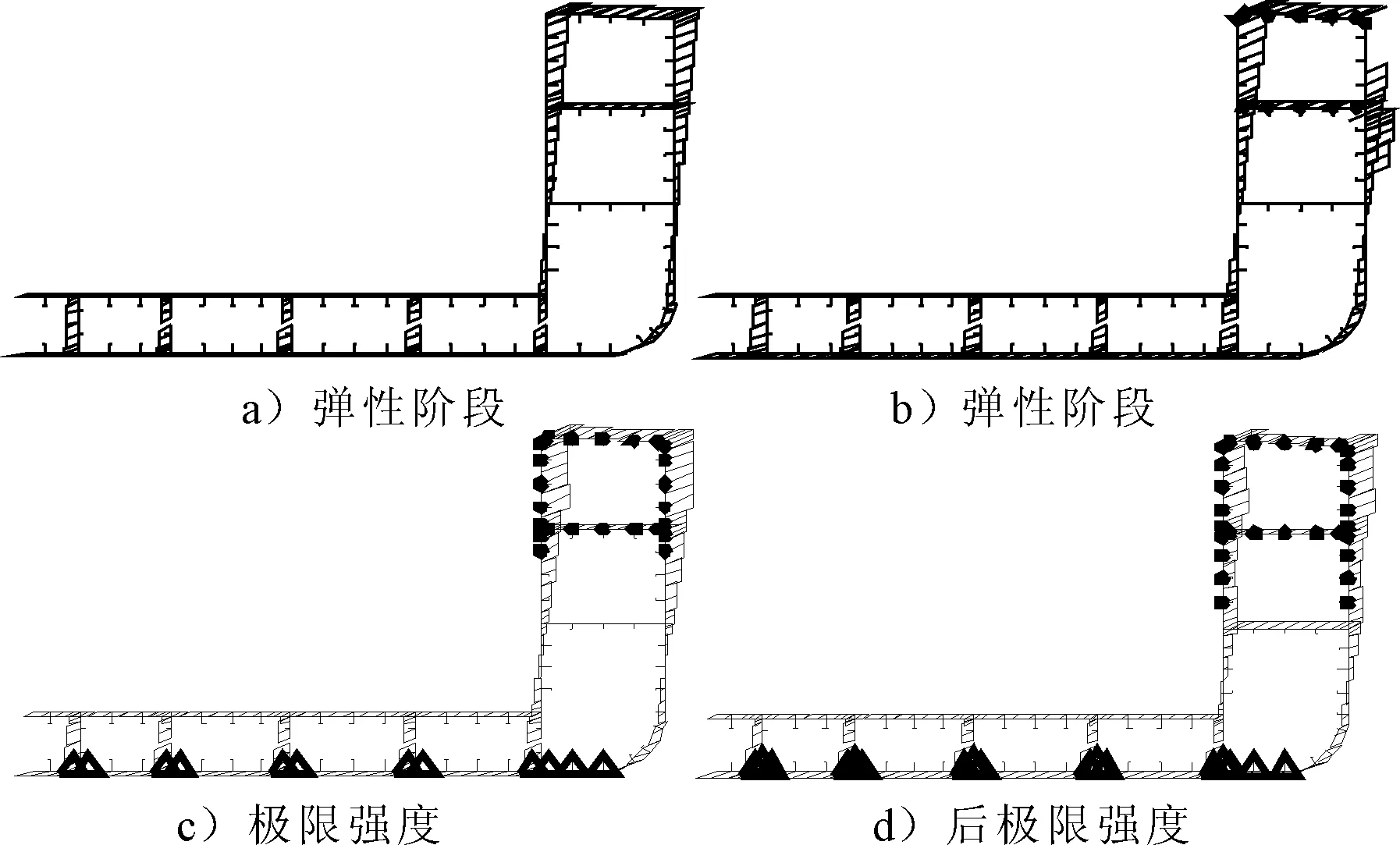
圖4 中垂狀況下不同載荷水平時各構件的應力分布

彎矩的最大值為1.26×106kN·m，此值即為中垂狀態下目標船的極限強度.

3 寬扁型江海直達船外載荷計算

江海直達航線涵蓋了江段和海段，江段所受波浪載荷很小，海段相對要大得多，因此遭受的波浪載荷具有間歇性，這與傳統的內河船或海船波浪載荷有顯著的不同.本文研究中先根據船舶航行的航線實際狀況來確定波浪載荷的概率水平，隨后選取能反映航區特征的波浪譜，根據該航區的波浪散布狀況進行波浪載荷長期預報，得到等效設計波高，然后按設計波理論進行外載荷直接計算.具體計算過程參見文獻[11].

3.1 外載荷計算模型

外載荷計算時，把船體看作剛體，建立僅外殼的濕表面模型和包括所有構件的質量模型，計算指定波浪條件下沿船體表面的壓力分布和相應的船體運動，將運動慣性力也視作外力，與船體表面壓力合在一起，成為作用于船體的外載荷.為了最大限度地減少載荷轉換誤差，載荷計算用外殼模型盡可能與結構計算模型的網格保持一致.

船舶的質量分布決定了浮態，進而影響其所受的外載荷.先把除主機、艙口蓋等較大質量的設備之外的空船質量沿船長方向分若干段，通過改變密度的方式分段模擬空船質量分布；主機、艙口蓋等重量較大設備按其作用區域以質量點的形式分布到相應位置；貨物質量按其作用區域分布到相應構件；油、水的質量通過改變相應油艙或水艙結構密度的方式施加到相應構件.最后，對三維質量模型進行檢查以確保其與設計狀態一致，尤其是重心縱向位置，如果誤差在1%以內，認為與設計狀態基本相符，否則需檢查誤差產生的原因，并進行修正，直到滿足要求為止.

3.2 波浪載荷預報

利用SESAM軟件中波浪載荷計算模塊WADAM，根據航線狀況確定的波浪譜、波浪散布圖和超越概率，考慮典型裝載工況，進行波浪載荷長期預報.相應的波浪特征參數的取值如下： ①波浪頻率的范圍從0.1～2.0 rad/s，間隔0.1 rad/s，波浪頻率數共20個；②浪向角從0°～180°，間隔30°，共7個浪向；③計算航速取為零，水深為無限水深.

對各工況下各種波浪特征參數的波浪載荷進行長期預報，得到各裝載工況的波浪載荷長期預報峰值及其對應的浪向、頻率等特征參數.滿載和壓載兩種典型裝載工況的波浪載荷長期預報峰值、對應的浪向、波浪頻率以及單位波高的響應、等效設計波高等特征參數見表2.

表2 波浪載荷預報結果

3.3 外載荷計算

作用于船體的外載荷包括靜水載荷和波浪載荷兩部分，波浪載荷已在上節中進行了計算分析，靜水載荷是由重力和浮力的差值引起，各裝載工況下重力分布會有所不同，從而靜水載荷也會不同.各裝載工況下靜水載荷的包絡線即為設計許用靜水載荷，將其與波浪載荷一起成為船體外載荷.

中拱狀態下最大許用靜水彎矩為2.200×108N·m，中垂狀態下最大許用靜水彎矩為-1.152×108N·m，故中拱狀態下最大外載荷為6.950×108N·m，中垂狀態下最大外載荷為-5.902×108N·m.

4 寬扁型江海直達船體結構安全裕度

船體結構極限承載能力和所遭受最大外載荷是船體結構安全可靠的兩個重要方面，二者的比值即為船體結構安全系數，代表著船體結構的安全裕度.明確船體結構的安全裕度，方能確切把握船體結構能抵抗極限海況的能力，或是在設計載荷下進行結構輕量化設計，在安全可靠前提下，探尋輕量化船體結構設計方案.

船體結構中拱和中垂狀態下的彎矩-曲率關系曲線及最大外載荷見圖5，彎矩-曲率關系曲線的最大值即為船體結構極限承載能力.中拱狀態和中垂狀態下船體結構極限承載能力、所遭受的最大外載荷及安全系數等總結見表3.中拱狀態下結構安全系數為1.942，中垂狀態下結構安全系數為2.135，說明目標船在設計載荷下可保持安全狀態，結構極限承載能力大約是最大外載荷的兩倍.

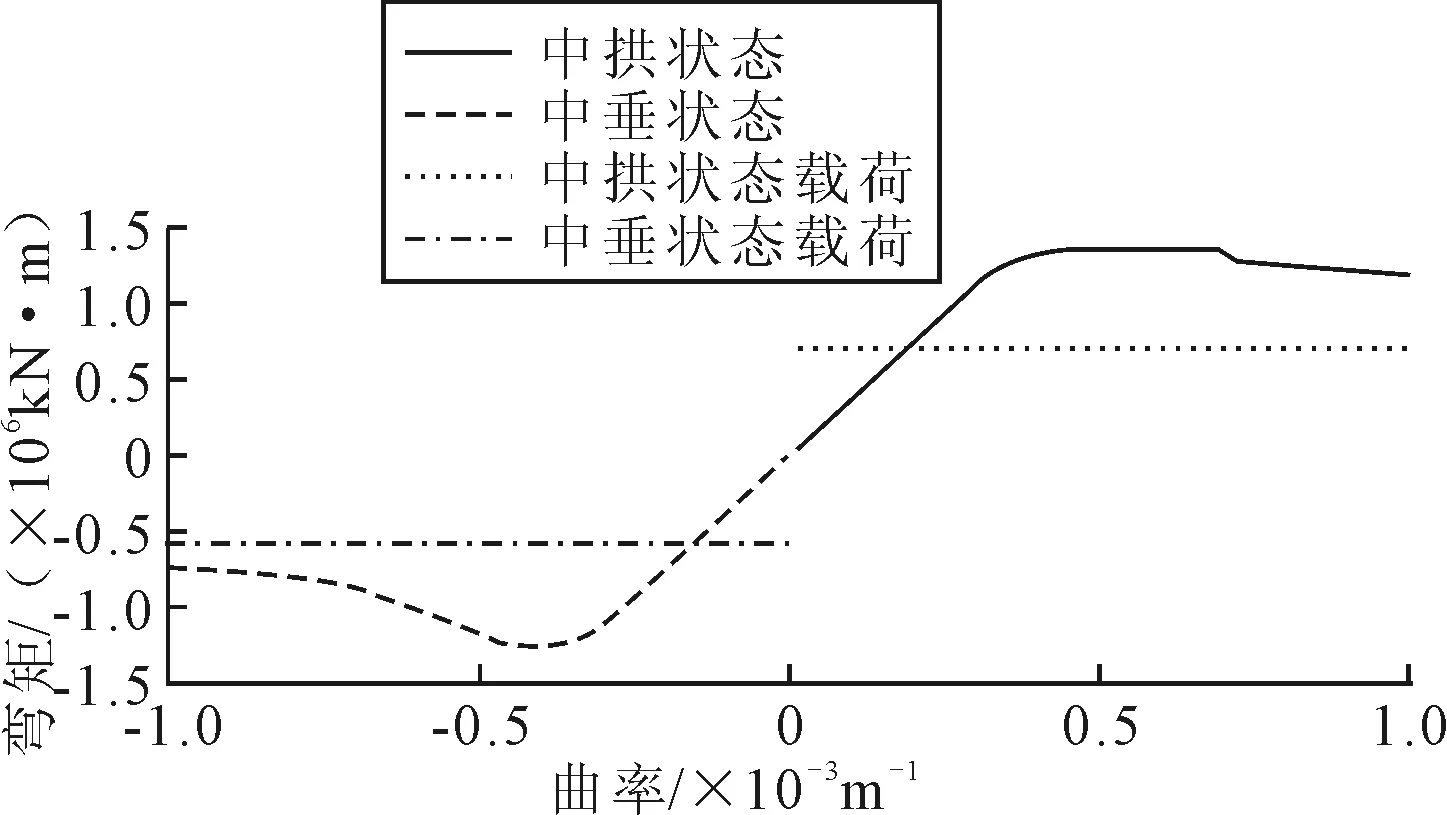
圖5 中拱和中垂狀態下船體結構彎矩-曲率曲線

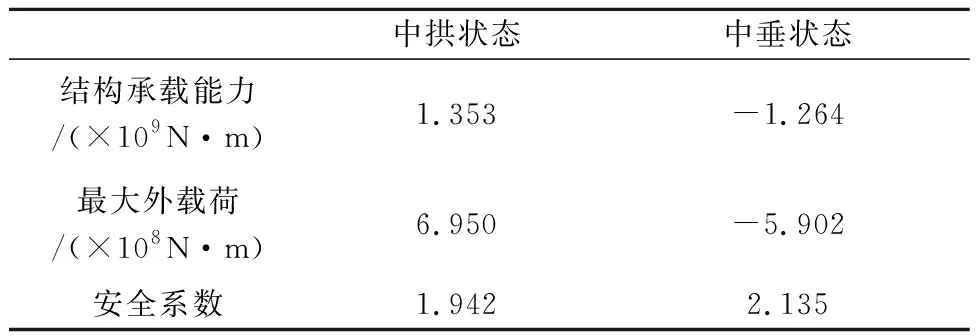
中拱狀態中垂狀態結構承載能力/(×109N·m)1.353-1.264最大外載荷/(×108N·m)6.950-5.902安全系數1.9422.135

5 結 束 語

長江由于天然航道的制約，船舶大型化唯有向船寬方向發展，研發寬扁肥大型船舶，本文以開發的武漢-寧波舟山航線“4E”級江海直達船舶為研究對象，該船寬深比達2.98，基于彈性大變形分析和剛塑性力學分析相結合的半解析方法獲得單元的平均應力-平均應變關系，采用Smith方法對該船進行逐次崩潰分析，獲得船體結構極限承載能力.隨后根據航線實際狀況來確定波浪載荷的概率水平，選定能反映航區特征的波浪譜，根據波浪散布狀況進行波浪載荷長期預報，按設計波理論進行外載荷直接計算以得到作用于船體的最大外載荷.

通過對“4E”級寬扁型江海直達船的船體結構極限強度和最大外載荷兩方面的計算分析，明確船體結構的耐力和所受到的外力，把握船體結構的安全裕度和抗極限海況的能力，為今后理性、合理、安全、可靠的船體結構最優化設計奠定基礎.

參考文獻

[1] 中國內河水運市場現狀調研與發展前景分析報告(2018-2025年)[R/EB].中國產業調研網，2017.http:∥www.cir.cn/R-JiaoTong Yun shu/85/NeiHeShui Yun DeFa ZhanQiao Jing.html.

[2] 柴俊凱.江海直達船極限強度研究及結構優化[D].武漢：武漢理工大學,2012.

[3] 傅何琪.江海直達運輸船極限強度研究[D].武漢：武漢理工大學,2013.

[4] NILVA V A,UKRAINE. Analytic method of definition of geometric characteristics of inland or river-sea navigation dry-cargo vessel after receiving damage[C]. The Asian-Pacific Technical Exchange and Advisory Meeting on Marine Structures，2015.

[5] NILVA V. A Residual strength assessment for mixed river-sea going dry going dry cargo vessel when part of longitudinal members are missed[J].Visnyk ONMU,2013,39:96-108.

[6] KHEDMATI M R, RASHEDI A R. Nonlinear finite element modelling and progressive collapse analysis of a product carrier under longitudinal bending [J]. Applied Ocean Research, 2014,48:80-102.

[7] PEI Z，FUJIKUBO M. Application of idealized structural unit method to progressive collapse analysis of a ship’s hull girder under longitudinal bending [C]. Proc of 15th Int. Offshore and Polar Engineering Conf, Montreal，2005.

[8] SMITH C S. Influence of local compressive failure on ultimate longitudinal strength of a ship’s hull [C]. PRADS,Tokyo,1977.

[9] YAO T, NIKOLOV P. Progressive collapse analysis of ship′s hull girder under longitudinal bending [J] Soc. Naval Architects of Japan, 1991,170:449-461.

[10] YAO T, ASTRUP O C, CARIDIS P, et al. Report of special task committee vi.2:“ultimate hull girder strength” [C]. Proc. 14th ISSC,Nagasaki, 2000.

[11] 姜偉，裴志勇，吳衛國.寬扁肥大型江海直達船結構強度探析[J].中國水運，2017(1):54-57.