移動荷載作用下索-橋耦合振動分析研究*

肖 祥 薛 浩 何雄君 陳燁君

(武漢理工大學交通學院1) 武漢 430063) (中建鋼構有限公司2) 深圳 518000)

0 引 言

拉索為斜拉橋的主要承重構件，一般長度較大，具有質量輕、柔度大和阻尼小等特點.因此，斜拉橋在車輛、風和地震等動荷載作用下的振動常誘發拉索的各種振動問題.自上世紀70年代，許多斜拉橋均發生了此類拉索大幅振動現象，如1976年，法國的Brotonne橋在將要完工時，幾根拉索發生了大幅度振動，并且觀察到了拍擊現象[1].1988年，比利時Wandre橋和Ben-Ahin橋在大風作用下，多根索發生了大幅振動[2]，荷蘭的Erasmus橋在通車1個多月后便由于斜拉索和橋面的大幅振動而導致關閉[3].同樣，上世紀90年代，我國楊浦大橋多根拉索產生了拍擊現象，南浦大橋也因拉索的振動導致拉索減振器的掉落.這種斜拉索和橋面的大幅振動對橋梁的安全運營和使用壽命均有極大的影響，因此，索-橋耦合振動問題也逐漸引起學者的關注.

目前，國內外已經有研究者對索-橋動力相互作用進行了研究.Leonhardt等[4]提出了系統阻尼的概念，認為當斜拉橋受到車輛、風、地震荷載時，拉索能夠為全橋結構的響應提供附加阻尼，這種阻尼歸咎于拉索的振動對橋梁結構響應的干擾.Causevic等[5]將拉索模擬成一系列彈簧和集中質量塊的組合，通過分析認為全橋的自振頻率不應該接近任意一根拉索的自振頻率，避免拉索大幅振動.Abdel等[6]通過對斜拉橋動力特性的分析，認為拉索的振動對全橋的動力行為有不利影響.亢戰等[7]建立了簡化的索-橋耦合振動參數模型，主要是將拉索簡化為集中質量-彈簧模型，從而得出了拉索在橋面振動激勵下產生耦合振動的可能性.陳水生等[8]建立了一種斜拉橋拉索與橋面耦合振動的非線性參數振動模型，分析了索的垂度、振動頻率和傾角對索-橋耦合振動的影響.李鳳臣等[9]建立了索-梁耦合的參數共振模型，推導了量綱一的量參激共振微分方程，對斜拉索2∶1參激共振進行了分析.上述研究主要針對索-橋耦合振動的參數分析，未涉及到移動荷載對斜拉橋索-橋耦合振動的影響.而近些年，由于城市的快速發展，車輛的客運量和貨運量都有了極大的提高，城市橋梁承受的車輛荷載越來越繁重，進而危及橋梁使用狀態和使用壽命.移動荷載對橋梁結構振動產生的影響已經成為影響橋梁使用壽命和安全運營不可忽視的因素，因此，分析移動荷載對斜拉橋索-橋耦合振動的影響較為重要.

本文在現有的研究成果基礎之上，建立了OECS(one-element-cable-stay)單索單元有限元模型和MECS(multiple-element-cable-stay)單索多單元有限元模型[10]，對橋梁索-橋耦合的動力特性進行了分析，對拉索的固有頻率與橋梁振動頻率之間的關系，以及對索-橋耦合振動的動力學影響進行了分析.接著開展了移動荷載作用下的橋梁結構索-橋耦合分析及其振動特性研究，并對該橋索-橋耦合振動隨車速的影響規律進行了分析研究，進而提出了減少索-橋耦合振動現象意見.

1 移動荷載作用下索-橋耦合振動分析模型

1.1 工程背景

西固黃河大橋起點于蘭州市定遠鎮，終點于黃羊頭，是連霍國道主干線蘭州南繞城高速公路的重點工程.西固黃河大橋為雙塔雙索面斜拉橋，跨徑組成為67 m+110 m+360 m+110 m+67 m，主梁采用工字鋼-混凝土結合梁，全橋共112根斜拉索，為4車道高速公路特大橋，車輛荷載等級為公路-I級，其立面圖及結合梁斷面見圖1.

圖1 西固黃河大橋立面圖及結合梁斷面圖(單位：cm)

根據主梁和橋塔形式，該橋斜拉索呈空間扇形索面布置，采用雙層HDPE防護的全防腐索體.斜拉索在塔上間距為1.8～2.5 m，根據實際錨固空間調整，在主梁縱橋向標準索距為12 m.根據各拉索的設計索力，斜拉索共有PES7-139，PES7-163，PES7-211，PES7-253，PES7-313五種.最大索長187.068 m，單根索最大質量17 t，拉索與水平面最小夾角為23.566°，斜拉索標準間距12 m，采用五種形式.材料參數見表1，由于每根拉索的索力不同，斜拉索的彈性模量也會不同，并且后續會進行Ernst公式換算，這里不予列出.

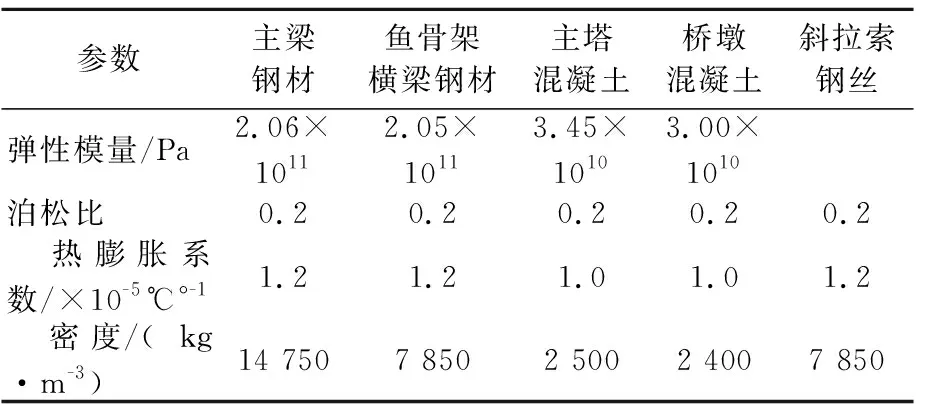
表1 西固黃河大橋材料參數

1.2 有限元模型

利用大型通用有限元軟件ANSYS分別建立西固黃河大橋OECS和MECS有限元模型.兩模型中橋面系均采用單主梁“魚骨架”模型，主梁工字鋼-混凝土結合梁采用截面等效的形式等效為單主梁.對于OECS模型，主梁、橋塔和橋墩采用Beam188單元模擬，斜拉索采用Link10單元模擬，并且每根斜拉索采用一個單元模擬，整個模型共采用了690個節點、455個單元，其中Beam188單元343個，Link10單元112個.對于MECS模型，主梁、橋塔和橋墩亦采用Beam188單元模擬，斜拉索則采用Beam4單元模擬，但拉索每3 m采用一個單元離散，單元截面特性與材料屬性均與OECS模型相同，模型共采用了4 727個節點、4 963個單元，其中Beam188單元343個，Beam4單元4 620個.此外，MECS橋梁模型中考慮了拉索初應力非線性剛度矩陣的影響.

斜拉索的垂度效應采用Ernst公式換算彈性模量予以考慮.

式中：γ為斜拉索重度；l為斜拉索水平投影長度；σ為斜拉索應力；E0為斜拉索鋼材彈性模量.

通過“初應力法”施加成橋索力，并根據“最小彎曲能量法”進行索力調整，經過累次迭代后得到最終的成橋索力.圖2為西固黃河大橋有限元模型.

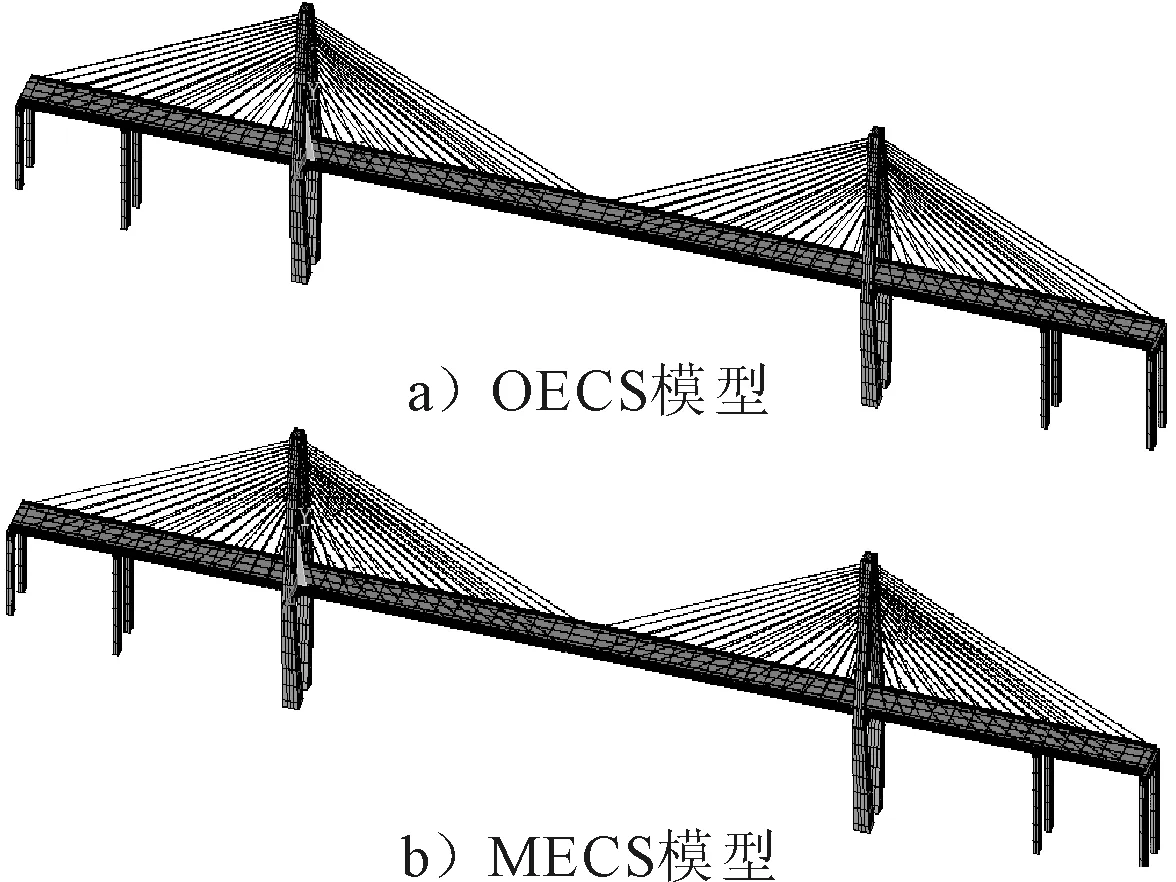
圖2 西固黃河大橋有限元模型

1.3 模態分析

采用Block Lanczos法求解西固黃河大橋有限元模型模態特征值和特征向量[11]，得到兩模型的各階模態.OECS模型主要出現的為主梁、橋墩和橋塔的振動模態，見圖3a)～c)，而MECS模型則出現了大量斜拉索及索-橋耦合模態，見圖3d)～i).

圖3 OECS模型及MECS模型模態

OECS和MECS兩種有限元模型計算的前6階模態的頻率見表2.由表2可知，兩模型前幾階模態的頻率有較大不同，MECS模型由于索-橋耦合振動現象頻率整體偏小；結合圖3和表2可知，索-橋耦合振動模態階數整體偏低.本文西固黃河大橋幾根典型斜拉索的固有振動頻率如表3所示.根據振動理論，斜拉索的固有頻率與橋梁的振動頻率為1∶1時，易出現索-橋耦合現象[12].由表3可知，該橋存在較多斜拉索振動頻率與橋梁振動頻率比接近于1的情況，這也是橋梁容易出現索-橋耦合現象的直接原因.

2 移動荷載作用下索-橋耦合振動分析

為考慮移動荷載對索-橋耦合的影響，分別基于OECS模型和MECS模型，利用ANSYS瞬態分析法施加移動荷載，車輛模型采用《公路橋涵設計通用規范》中標準大型貨車[13]，見圖4a).為簡化計算，本文采用多個移動集中力和等效力矩的形式施加移動荷載，并考慮車輛在3號車道由定遠鎮開往黃頭羊方向，移動速度為20 m/s，車輛布置情況見圖4b).

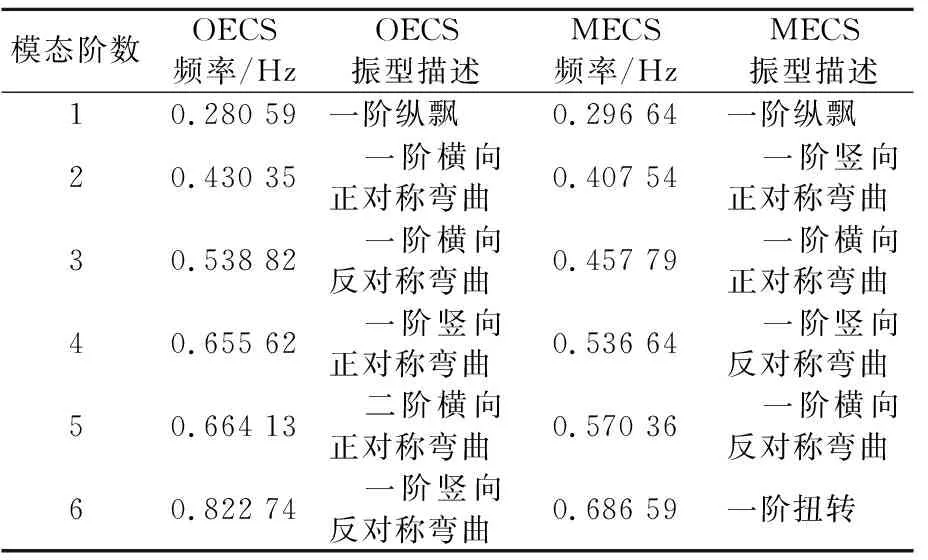
表2 OECS和MECS模型頻率對比

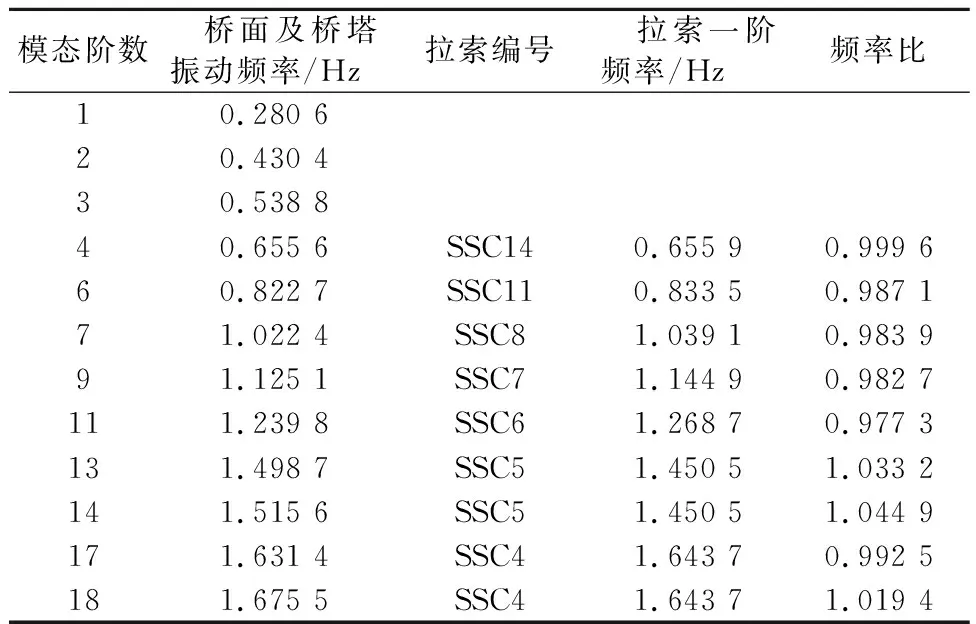
表3 拉索與橋面橋塔一階頻率對比

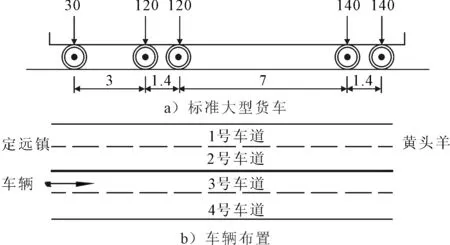
圖4 標準大型貨車及車輛布置(單位：尺寸，m；荷載：kN)

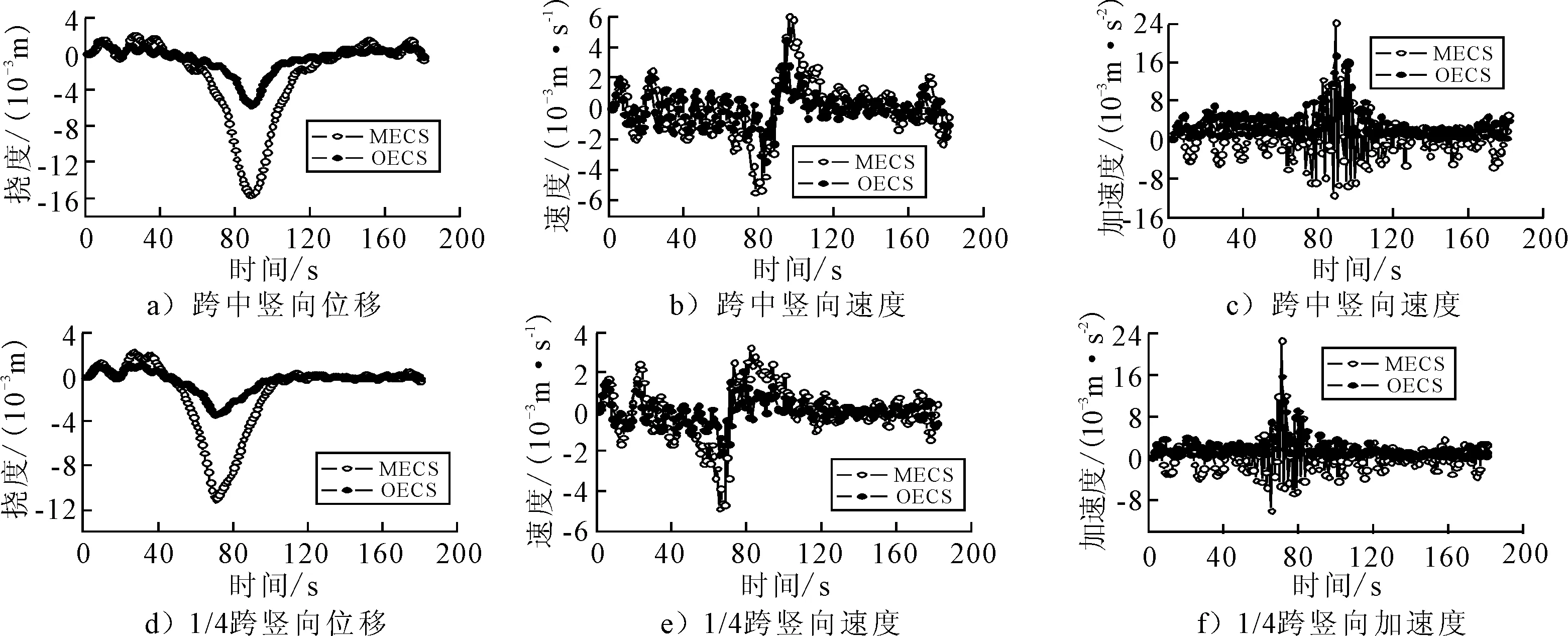
圖5 跨中及1/4跨動力響應

采用OECS與MECS兩種模型進行移動荷載作用下的振動響應分析，得到橋面跨中的位移、速度、加速度時程對比曲線見圖5.圖5中實心點線表示OECS模型計算結果，空心點線為MECS模型計算結果.其中圖5a)中MECS模型最大撓度為-15.7 mm，OECS模型最大撓度為-5.6 mm，兩者相差10.1 mm；圖5b)中MECS模型最大速度為0.006 m/s，OECS模型最大速度為0.004 m/s，兩者相差0.002 m/s；圖5c)中MECS模型最大加速度為0.024 m/s2，OECS模型最大加速度為0.017 m/s2，兩者相差0.007 m/s2；圖5d)中MECS模型最大撓度為-11.0 mm，OECS模型最大撓度為-3.4 mm，兩者相差7.6 mm；圖5e)中MECS模型最大速度為-0.005 m/s，OECS模型最大速度為-0.002 m/s，兩者相差0.003 m/s；圖5f)中MECS模型最大加速度為0.023 m/s2，OECS模型最大加速度為0.016 m/s2，兩者相差0.007 m/s2；這些計算結果表明當考慮索-橋耦合時，橋梁撓度明顯大于不考慮索-橋耦合的情況，速度和加速度幅值也明顯大于不考慮索-橋耦合的計算結果，其中位移最大差別達到64.3%.由此可知，在移動荷載作用下索-橋耦合的影響不容忽視，應在橋梁設計與分析中予以重視.

進一步考慮在不同車輛荷載移動速度下，進行動力響應時程分析.計算得到移動速度在5～35 m/s(速度間隔為5 m/s)內變化時的動力響應，見圖6.圖中空心方塊點線和空心三角點線分別為OECS模型和MECS模型跨中撓度隨速度的變化曲線，空心圓點線和實心三角點線分別表示OECS模型和MECS模型1/4跨撓度隨速度的變化曲線.

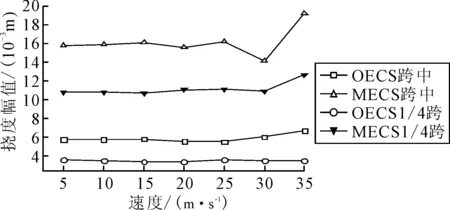
圖6 跨中及1/4跨撓度幅值變化曲線

由圖6可知，MECS模型與OECS模型計算得到的跨中及1/4跨的撓度幅值曲線總體變化較為平緩，MECS模型的計算結果明顯大于OECS模型，符合前述變化規律.但當車速達到35 m/s，兩種模型幅值差別明顯加大，但在設計車速范圍以內(30～70 km/h)，幅值差別變化不明顯.

文獻[7]研究了拉索振動響應與拉索錨固點處橋面振動(激勵)間的關系，但這種研究基于簡化模型開展.因此，本文基于MECS模型，對主梁斜拉索錨固點與斜拉索的振動響應間的關系進行了進一步分析.上文模態分析表明邊索更容易與橋面發生耦合振動，因此,以最接近跨中位置的拉索SMC14為例進行分析.SMC14索基準長度為183.708 m，成橋索力6 069.6 kN，傾角23.566°，單位索重100.5 kg/m.當車速為20 m/s時，拉索跨中及主梁錨固點的垂向位移和加速度時程曲線見圖7.根據SMC14跨中及錨固點的動力響應對比分析可知，當移動荷載距離拉索較遠時，拉索跨中和錨固點的振動均不明顯；移動荷載距離拉索越近，拉索跨中和錨固點的振動幅值越大，且拉索跨中和錨固點的振動規律基本一致，但拉索跨中的振動幅值明顯大于錨固點，該計算結果也符合實際情況，總體振動規律與文獻[7]一致.根據斜拉索與錨固點的振動規律，可以在每根斜拉索錨固端附近增設與該索振動頻率相對應的振動阻尼器以減弱斜拉索的振動，從而減少或減弱索-橋耦合振動現象.

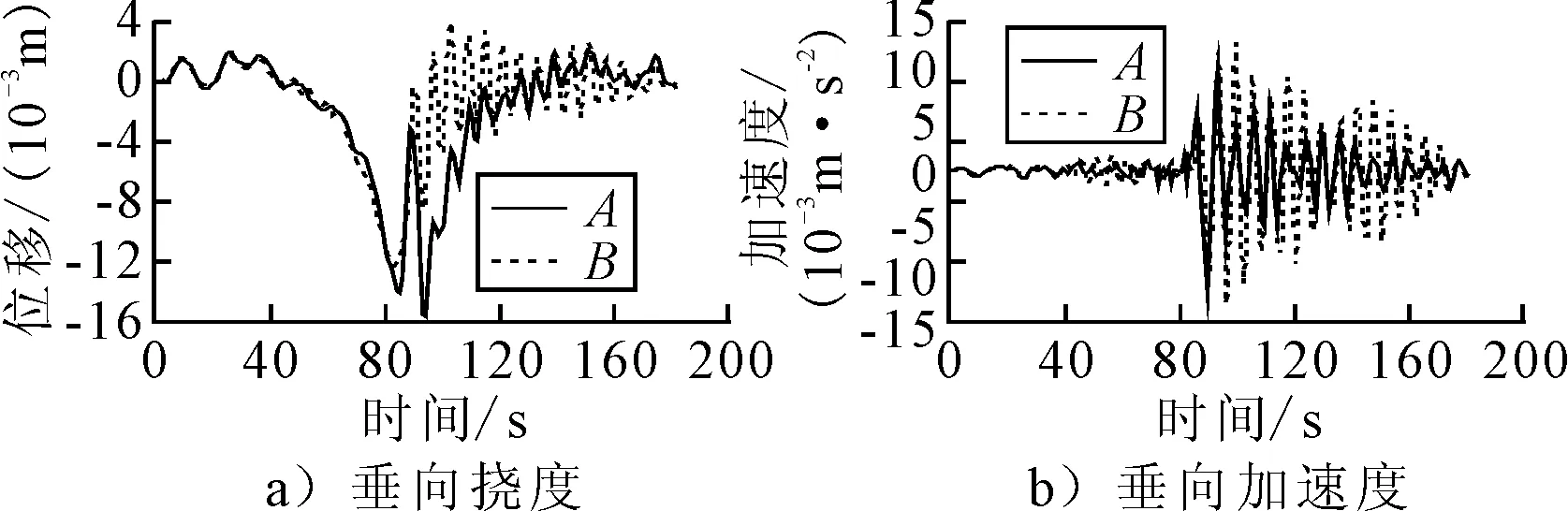
圖7 SMC14索跨中及錨固點動力響應對比

注：A為錨固點響應，B為拉索跨中響應

3 結 論

1) 在移動荷載作用下，當考慮索-橋耦合時，橋梁的動力響應明顯大于不考慮索-橋耦合的情況，因此索-橋耦合現象對橋梁振動和車輛運行的影響不可忽視.

2) 移動荷載速度很大時，速度對該橋動力響應幅值有一定影響；但在設計車速范圍以內，移動荷載速度的大小對橋梁動力響應的幅值影響較小.

3) 索橋耦合振動的拉索分析表明拉索錨固點與拉索的振動規律基本一致，但拉索的振動幅度明顯大于錨固點.因此在斜拉索錨固端增設阻尼器來減弱或減少索-橋耦合，從而減弱橋梁疲勞程度，延長橋梁使用壽命.

參考文獻

[1] STIEMER S F, TAYLOR P, VINCENT D H C. Full scale dynamic testing of the Annacis Bridge[J]. IABSE Periodica,1988(1):1-16.

[2] LILIEN J L, PINTO D C A. Vibration amplitudes caused by parametric excitation of cable stayed structures [J]. Journal of Sound and Vibration,1994(2):69-75.

[3] REUSINK J, STAALDUINEN P V, VROUWENVELDER T, et al. Numerical modelling of rain-wind-induced vibration: erasmus bridge, rotterdam [J]. Structural Engineering International,1998,8(2):176-184.

[4] LEONHARDT F, ZELLNER W. Cable-stayed bridges[J].IABSE Surveys,1980(1):55-59.

[5] CAUSEVIC M S, SRECKOVIC G. Modelling of cable-stayed bridge cables: effects on bridge vibrations[J]. Experience and Practice,1987(1):407-412.

[6] ABDEL G A, KHALIFA M A. Importance of cable vibration in dynamics of cable-stayed bridges [J]. Journal of Engineering Mechanics,1991,117(11):2571-2589.

[7] 亢戰,鐘萬勰.斜拉橋參數共振問題的數值研究[J].土木工程學報,1998(4):14-22.

[8] 陳水生,孫炳楠.斜拉橋索-橋耦合非線性參數振動數值研究[J].土木工程學報,2003,36(4):70-75.

[9] 李鳳臣,張麗娜,楊鷗,等.考慮索-梁耦合的斜拉索2∶1參激共振分析與數值模擬[J].應用基礎與工程科學學報,2015,23(5):966-980.

[10] TULADHAR R, DILGER W H, ELBADRY M M. Influence of cable vibration on seismic response of cable-stayed bridges [J]. Canadian Journal of Civil Engineering,1995,22(5):1001-1020.

[11] 王浩,李愛群.ANSYS大跨度橋梁高等有限元分析與工程實例[M].北京:中國建筑工業出版社,2014.

[12] 魏曉軍.大跨度斜拉橋索-橋耦合振動[D].長沙:中南大學,2011.

[13] 中華人民共和國交通部.公路橋涵設計通用規范:JTG D60—2004[S].北京:人民交通出版社,2004.