平面傳感器陣列測試振動角速度算法研究

趙天賀， 汪 偉， 寇博晨， 沈晨暉， 孫中興

(陸軍工程大學石家莊校區，河北 石家莊 050003)

0 引 言

現代武器裝備發展迅速，為了提升飛機、坦克、火炮等的使用性能，使其在復雜戰場環境下能夠更好地完成任務，需要對其產生的運動參數進行監控[1]。這類運動體運動自由度大、動態范圍廣，振動狀態為較高頻率下多維線振動和角振動的耦合[2]。單維的傳感器測試技術、陀螺儀技術、CCD成像技術等傳統振動測試手段很難在該測試環境中得到應用[3]。加速度傳感器陣列可以有效地對該類振動進行監測，解決了工程中對上述運動體進行六自由度參數測試的難題[4]。

近年來，國內外加速度傳感器陣列的配置方案越來越多，典型的傳感器配置方案有六加速度、九加速度、十二加速度陣列構型[5-6]。在工程實現過程中，發現空間配置方案會增大測量設備的體積，本文通過對構型設計的深入研究，設計了一種基于平面的加速度傳感器配置方案，解決了測量設備的體積問題。

采用加速度傳感器陣列測量六自由度參數，角速度的解算非常關鍵，其準確度直接影響著最終測量結果的準確性。目前，傳統的角速度解算方法有積分法、開方法等。在新的構型當中單一的積分法會隨著時間的積累產生嚴重的發散型誤差，單一的開方算法得不到含有符號的解算值，組合的開方法會產生嚴重的小角度誤判現象。本文在對算法進行原理推理和仿真分析的基礎上，通過比較其優缺點及分析加速度傳感器輸出方程，設計了多種角速度融合的組合方法[7]，可以使角速度的誤差滿足允許范圍，具有較大的實用價值。

1 傳感器陣列測試方案

安裝配置方式如圖1所示，O-XYZ為建立的載體坐標系，在O-XY平面內安裝3個三軸加速度傳感器時，分別使傳感器的一個敏感軸重合安裝于X軸或Y軸坐標軸，另外兩軸垂直于該坐標系。其中分別為3個三軸加速度傳感器在坐標軸上的安裝位置。分別代表的距離，代表傳感器不同敏感軸方向的編號。

9個傳感器相對于載體坐標系原點的位置坐標矩陣r和敏感方向坐標矩陣θ為

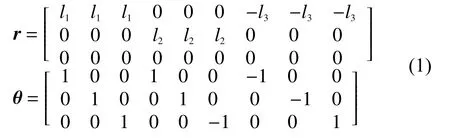
根據運動學方程可以得到基于線加速度計捷聯慣導系統上任意加速度計的輸出[8-10]為

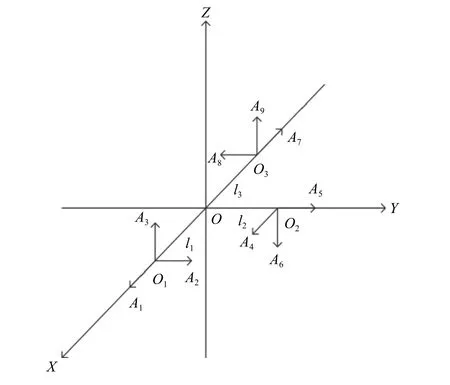
圖1 平面加速度計陣列安裝示意圖

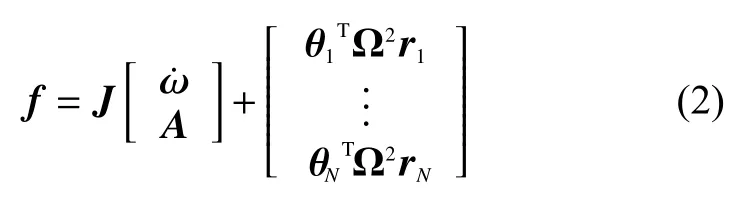
式中：——加速度傳感器上測量到的加速度信號；

——構型矩陣；

——的反對稱矩陣；

A——載體坐標系3個坐標軸方向上的線加速度。

其中：

將式(2)完全展開可以得到關于載體坐標系的角速度、角加速度和線加速度等變量，與9個加速度傳感器在其敏感方向上加速度信號的方程組為

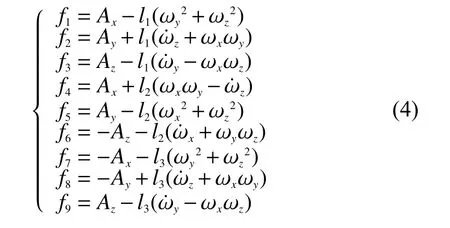
根據式(4)可以解算得到表征六自由度的相關參數的相互關系表達式為

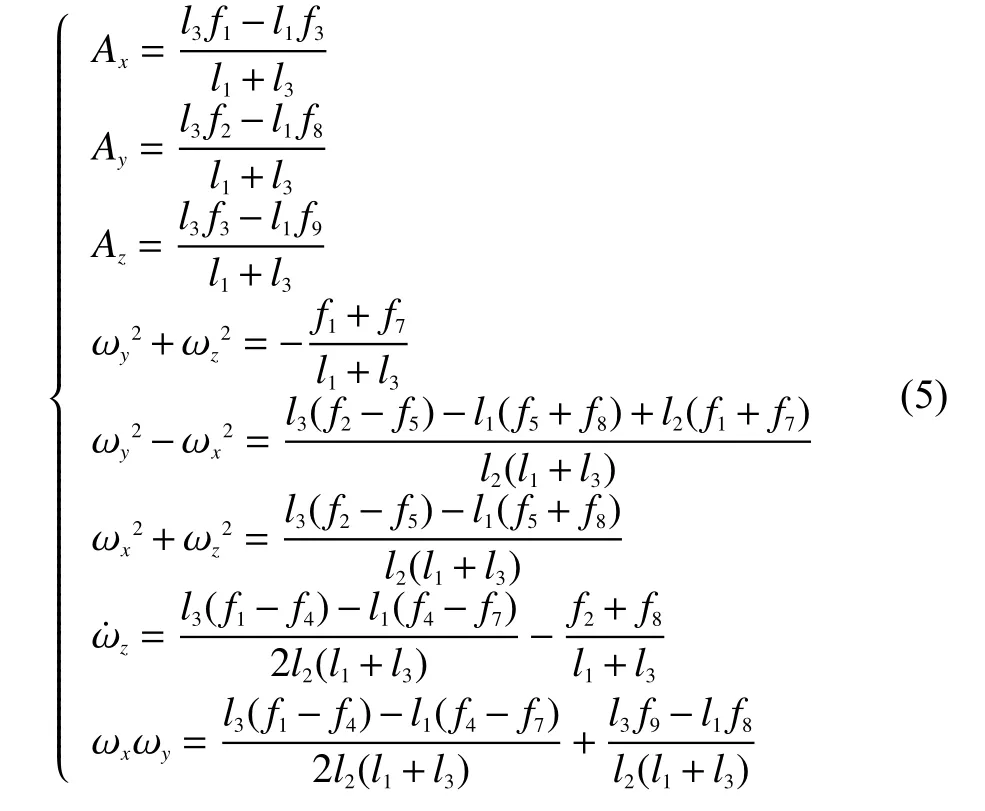
2 角速度解算方法的設計

應用式(5)解算得到的角速度平方項、Z軸的角加速度以及角速度的乘積項，可以應用積分法、開方法和組合算法求解3個坐標軸的角速度。

2.1 積分法

在載體坐標系初始時刻角速度值已知的情況下，根據式(5)通過直接積分解算3個坐標系的角速度。設置坐標系角速度初始值為ωx(0)、ωy(0)、ωz(0)，在采樣周期?t較短時，近似認為采樣時刻距下一采樣時刻時間間隔內角速度均勻變化。已知Z軸角加速度的情況下，可以采用直接積分的算法求得ωz(t)，如下所示：

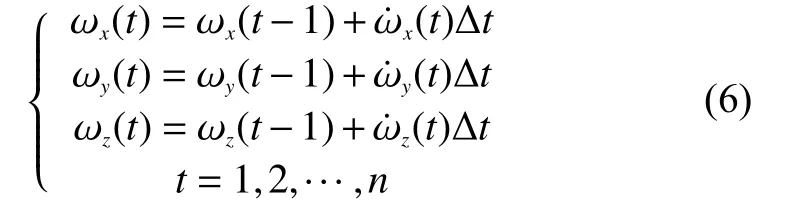
將解算的ωz(t)、ωx(0)、ωy(0)代入式⑷獲得直接積分求得ωx(t)、ωy(t)，解算值作為循環計算[11]。應用該算法進行角速度解算，誤差來源于將兩采樣點之間的角加速度值認為是恒定值，并且積分法造成誤差隨時間的延長不斷積累，通過提高采樣頻率可以在很大程度上降低此類誤差。由于其不可避免性，在長時間振動參數的測量過程中容易產生較大誤差。

2.2 開方法

根據式(5)中的平方項可以求得但無法直接得到3個坐標軸角速度絕對值的符號。應用積分法解算的ωx(t)、ωy(t)、ωz(t)作為開方法中角速度絕對值的符號sign(ωx(t))、sign(ωy(t))、sign(ωz(t))，求解開方法的解算角速度表達式為

應用開方法進行角速度的解算過程中，解算數值不隨時間積累，避免了較大誤差的產生，但其應用的是積分法解算值的符號，仍然存在符號誤判的現象，隨著時間的積累，符號誤判對結果的影響持續增大。

2.3 組合算法

通過對多種解算方法的分析與比較，針對平面加速度陣列構型設計了一種積分法、開方法相結合的組合算法進行角速度的解算[12]，應用開方法中獲得的ωz(t)為組合算法的Z軸角速度解算值。根據無陀螺捷聯慣導系統相關對準技術設置X軸、Y軸初始角速度[13]為將其代入式(4)，獲得應用進行積分運算，并將積分值符號作為的符號，并將其乘積作為角速度解算值。組合算法通過對初始值的不斷更新，避免了積分法誤差隨時間而不斷積累的問題，又通過開方法持續獲得精確的角速度絕對值，二者相結合可以獲得精確且不隨時間積累的角速度結算值。

3 仿真分析

為了驗證針對平面構型設計的角速度解算算法的可行性，搭建模型對其進行比較和分析。在仿真中取采樣頻率為1 kHz，采樣時間為1 000 s，加速度傳感器常值誤差為0.000 1g，隨機噪聲的均方差為0.001g。

角速度參數設置為

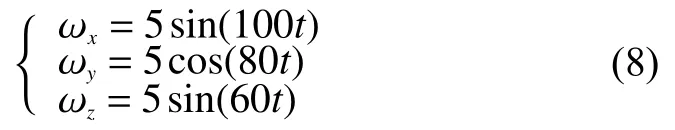
線加速度參數設置為

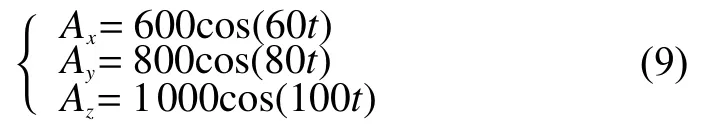
對3種算法進行仿真，并分別對其X軸、Y軸角速度誤差進行分析，如圖2～圖4所示。

從圖2可以看出，積分法解算的角速度誤差隨時間不斷積累發散。當測試時間較短時，誤差較小，但一旦時間增長，其誤差呈指數形式增長。由此可見，該算法不可應用于平面加速度傳感器陣列的姿態解算當中。

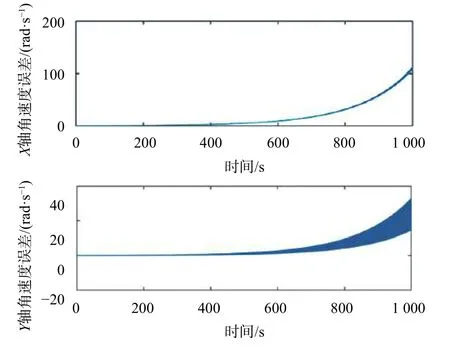
圖2 積分法角速度誤差

圖3 開方法角速度誤差

從圖3開方法仿真曲線可以看出，角速度誤差在隨著時間積累到10 rad/s后將不再增長。仿真說明開方法雖然解決了單一的積分法的誤差積累問題，但開方法中的積分獲取符號成分對其造成的符號誤判現象隨著時間的延長不斷嚴重，難以獲得較真實的角速度解算值。因此結合積分法的開方法也很難應用到新的構型當中。

從圖4組合算法仿真可以看出，組合算法解算的角速度誤差穩定在10?4量級，沒有出現誤差隨時間積累的現象，也不會出現符號誤判的現象，且始終保持解算結果的高度精確性，滿足誤差允許范圍。仿真說明組合算法通過對初值的更新，解決了改進開方法的符號誤判問題，保證了解算數據的準確性。組合算法的提出，為下一步的姿態解算提供了可靠的初始解算數據，是一種有效的解算方法。

4 結束語

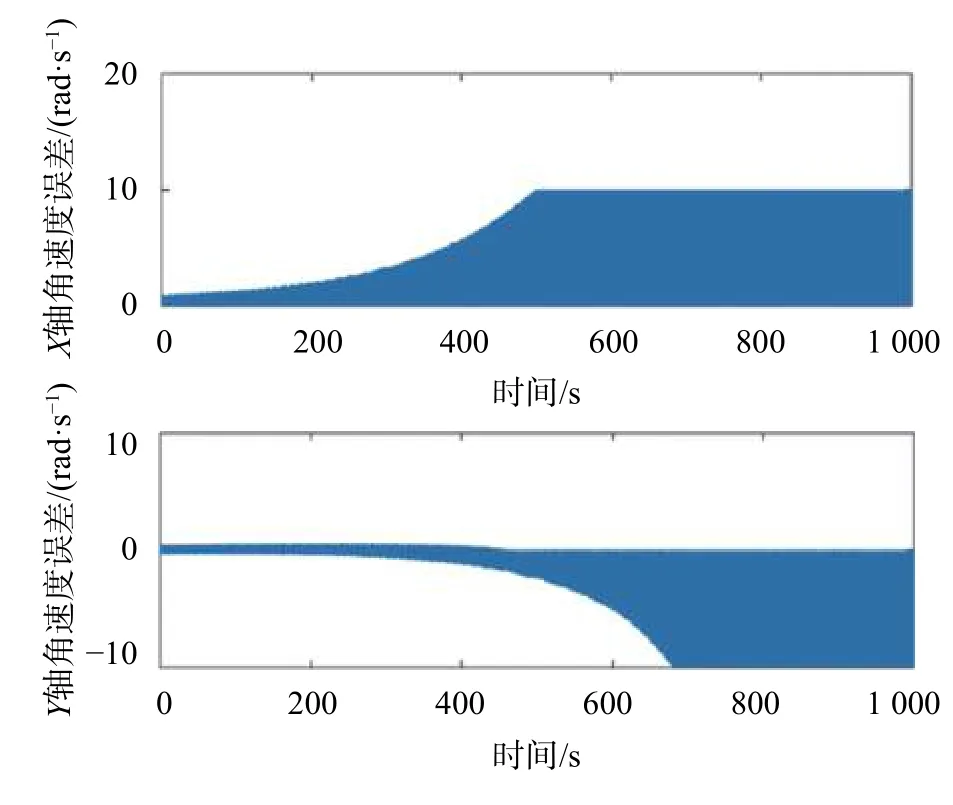
圖4 組合算法角速度誤差

為實現傳感器陣列技術在運動體復雜振動測試領域的工程應用，設計實際符合要求的傳感器配置方案。該文介紹一種平面傳感器陣列，角速度解算作為傳感器陣列振動測試的關鍵環節。針對新的構型，通過學習傳統解算手段設計3種解算方法，其中積分法誤差隨時間積累嚴重，開方法符號誤判不可避免。組合算法有效地避免積分算法的誤差積累和小、角速度的符號誤判問題，在長時間的仿真計算過程中仍然能保持較高準確度，對傳感器陣列振動測試技術的工程實現具有一定的意義。

[1]趙天賀, 汪偉. 基于MEMS技術的捷聯慣導系統現狀[J]. 飛航導彈, 2017(10): 17–21.

[2]汪偉, 焦健超, 唐力偉, 等. 基于傳感器陣列的振動測試角速度算法研究[J]. 中國測試, 2012, 38(4): 58–61.

[3]焦健超. 火控系統觀瞄器件復雜振動環境參數測試技術研究[D]. 石家莊：陸軍工程大學石家莊校區, 2011.

[4]焦健超, 汪偉, 唐力偉, 等. 三軸加速度傳感器陣列振動測試新方案[J]. 中國測試, 2012, 38(3): 109–112.

[5]楊杰. 無陀螺捷聯慣導系統加速度計構型研究與誤差分析[D].哈爾濱：哈爾濱工程大學, 2011.

[6]王東江, 楊新民. 一種無陀螺捷聯慣導的九加速度計測姿方法[J]. 電子測量技術, 2017, 40(10): 70–74.

[7]QIN F J, LI A, XU J N. Design of attitude algorithm for 13–accelerometer based inertial navigation system[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 637–641.

[8]湯傳業. SINS/GPS組合測量中的捷聯算法與組合濾波技術研究[D]. 南京：東南大學, 2016.

[9]王菲. SINS/GPS組合導航系統研究[D]. 北京：北京理工大學, 2015.

[10]汪偉, 歹英杰, 陳海龍, 等. 獨立卡爾曼濾波器全加速度計復雜振動角速度解算[J]. 中國測試, 2017, 43(5): 105–109.

[11]陳海龍. 基于加速度計陣列的裝備六自由度復雜振動測試技術研究[D]. 石家莊：軍械工程學院, 2013.

[12]李成剛, 謝志紅, 尤晶晶, 等. 新型無陀螺捷聯慣導系統導航方案設計及建模[J]. 中國慣性技術學報, 2015, 23(3):303–310.

[13]張慧. 捷聯慣導系統自對準技術研究與仿真[D]. 太原：中北大學, 2016.