基于正交試驗的應變片敏感柵結構參數的優化

許藝青， 楊曉翔， 韋鐵平， 姚進輝

(1. 福州大學石油化工學院，福建 福州 350116; 2. 福州大學機械工程及自動化學院，福建 福州 350116; 3. 泉州師范學院, 福建泉州 362000; 4. 福建工程學院機械與汽車工程系，福建 福州 350118; 5. 福建省計量科學研究院，福建 福州 350003)

0 引 言

電阻應變片廣泛應用于工程結構、應變測量及制造各種物理量傳感器，特別是測力傳感器、稱重傳感器和壓力傳感器等領域，因此，電阻應變片的測量結果的可靠性和準確性尤為重要[1]。Vadivuchezhian等[2]和Subrahmanya等[3]研究膠粘劑材料及其厚度對電阻應變片應變測量的影響，結果表明隨著膠結層厚度的增加，應變損失增大。Komurlu等[4]將電阻應變片粘貼在混凝土上，對氰基丙烯酸酯、聚氨酯和環氧樹脂膠粘劑進行試驗對比，結果表明氰基丙烯酸酯在應變片測量結果中最準確。Zike等[5]建立基體和電阻應變片的三維模型，研究了彈性模量從1～200 GPa的基體材料對應變測量的影響，并進行修正。Zhou 等[6]提出了一種應變片布置優化的通用框架，并結合案例分析驗證了框架的有效性，為結構性能評估的實際應用提供了方便。張佳明等[7]建立高溫應變片參數高精度標定裝置，確定影響高溫應變片測量結果的參數，并進行補償。王文瑞等[8-9]自主研制絲式高溫應變片，建立簡支梁、膠層、敏感柵有限元模型研究敏感柵結構參數對測量精度的影響，結果表明絲式敏感柵越細測量精度越高；高溫應變片的敏感柵間距與長度具有精度最優值。胡玉梅等[10]建立含應變片的懸臂梁模型，分析了絲式應變片敏感柵不同的直徑、柵長、柵絲間距對應變傳遞誤差的影響，結果表明柵長、柵間距在基體應變傳遞中具有中間最優值，柵絲直徑越小應變傳遞誤差越小。尹福炎[11]利用有限元法研究了不同敏感柵的材料、厚度和端環長度等對應變片性能的影響。

由上可知，對電阻應變片的研究主要集中在粘貼工藝、膠粘劑材料、絲式應變片結構參數及溫度對其性能的影響，對箔式電阻應變片敏感柵幾何參數對應變傳遞的影響研究較少，而且大部分研究都是單一變量。為此，本文建立了等強度梁、基底和箔式敏感柵所組成的測量模型，采用正交試驗對電阻應變片敏感柵材料、柵絲厚度、柵長和柵絲間距等因素進行了參數組合設計，利用ANSYS有限元軟件進行分析，揭示這些因素對應變片性能和應變傳遞誤差影響，找出最佳組合方案和不同參數的影響主次，為電阻應變片的結構設計和應變片的選擇提供了依據。

1 電阻應變片工作原理

電阻應變片的工作原理是基于金屬的應變效應。應變片借助于各種膠粘劑粘貼于試件表面，當試件受力產生變形時，應變片敏感柵也隨之發生變形，引起阻值發生相應的變化，再把這一電阻變化轉換為電信號變化輸出。

電阻應變片主要由基底、敏感柵、覆蓋層及引線等組成，其結構如圖1所示。基底和覆蓋層由絕緣材料制成，起保護和固定敏感柵的作用。敏感柵是把應變量轉換成電阻變化量的部分，常用的箔材有銅鎳合金、鎳鉻合金、鐵鉻鋁合金和鉑銥合金等金屬材料，其厚度一般取1～5 μm，柵長根據使用目的不同，有0.2 mm到幾百毫米，柵絲間距由使用條件來選定，一般來說柵絲間距的大小是整數倍的單柵絲寬度。

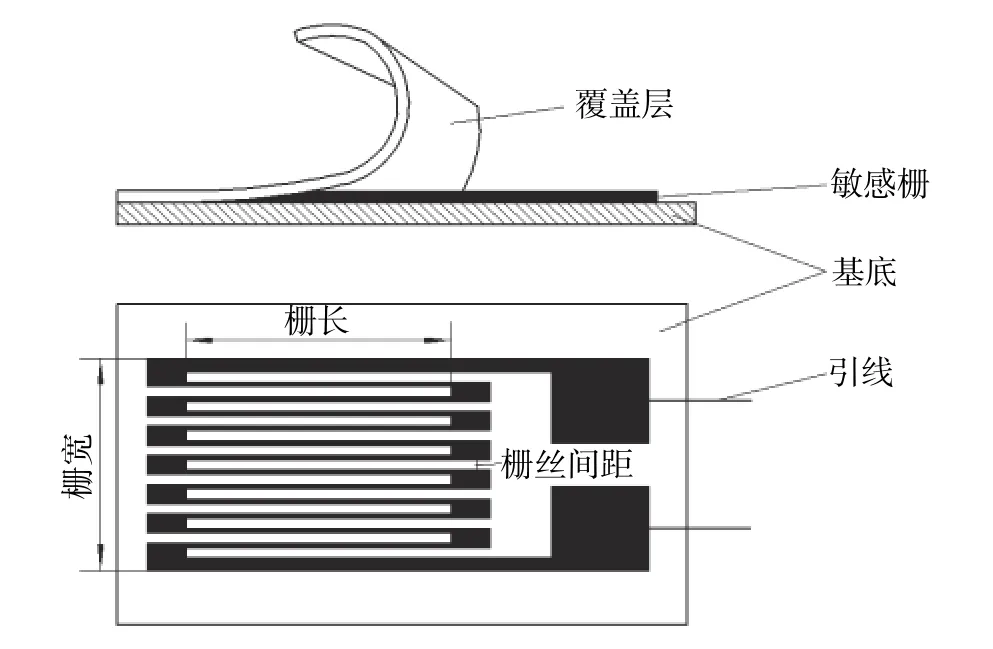
圖1 電阻應變片的典型結構

2 有限元模型建立和分析

為了解電阻應變片測量規律，取某型號120 Ω的電阻應變片，建立了含等強度梁、敏感柵和基底的三維簡化模型，各部分的力學性能如表1所示。對等強度梁與應變片粘貼處進行網格加密劃分，有限元網格模型如圖2所示。各部分均采用八節點六面體實體單元solid185，模擬時將等強度梁左端全約束，在右端施加載荷50 kN。

表1 各部分力學性能和幾何尺寸[12]

圖2 有限元網格模型

圖3為等強度梁y向（沿梁的軸線方向）應變云圖，可以看出，等強度梁最大應變8.08×10-4，發生在固定端處，提取等強度梁貼片位置中間20個節點的應變εs為6.90×10-4。

圖3 等強度梁y向應變云圖

圖4、圖5分別為敏感柵和基底沿y方向（柵絲方向）應變云圖，從圖4可知，敏感柵所受最大應變為1.055×10-3，最小應變為5.05×10-4，每根柵絲中間受力較均勻，并向兩端逐漸遞減，兩端所受的應變幾乎為0。從圖5可知，基底在與敏感柵邊界交界處發生應變突變，所受最大應變為1.018×10-3，最小應變為0.105×10-3，基底兩端應變幾乎為0。取應變片敏感柵中間20個節點y向應變的平均值εh為6.84×10-4，作為應變片的測量值。

圖4 敏感柵沿y軸方向應變云圖

圖5 基底沿y軸方向應變云圖

由文獻[13]可知，等強度梁與敏感柵的應變傳遞率為

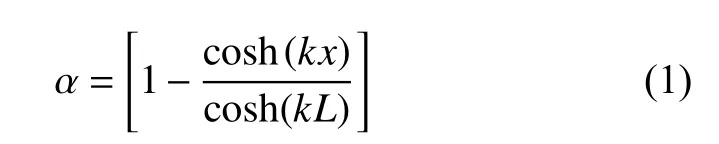
式中：k—剪滯系數，

tm、Wm、Gm—基底厚度、寬度和剪切模量；

tg、Wg、Eg—敏感柵厚度、寬度和彈性模量；

n—柵絲數目。

將各部分幾何參數帶入式（1）可得應變傳遞率的理論值，有限元應變傳遞率為敏感柵和等強度梁有限元應變值的比值。理論解與有限元解的對比如表2所示，理論解與有限元解應變傳遞率誤差為0.8%，由于建模時對模型進行簡化處理，故有限元結果與理論值存在一定誤差，仿真結果與理論值計算基本一致。

3 敏感柵結構參數對應變傳遞的影響

3.1 正交試驗設計及結果

由工程經驗可知，應變片的性能特性，不僅與所用的箔材材料、膠粘劑和制作工藝等有關，而且還與應變片敏感柵結構的幾何形狀密切相關。在設計箔式應變片時通常考慮敏感柵的材料、箔柵厚度、柵長和柵寬等。因此，本文基于有限元法，結合正交試驗，綜合分析以上參數對電阻應變片應變傳遞的影響。

表2 理論解與有限元解對比表

選擇如下4個影響因素：箔柵材料（A），柵絲厚度（B），柵長（C），柵絲間距（D）。每個因素取3個水平，如表3所示。

為便于描述，A的3個水平分別用A1、A2、A3表示，以此類推。

若全面試驗則有81個水平組合，如A1B1C1D1，A1B1C1D2，A1B1C1D3等,全面試驗要求的試驗太多，因此采用正交試驗，采用L9（34）正交表，按4因素3水平安排試驗，從而選擇最佳的敏感柵結構參數，試驗模擬結果如表4所示。

表3 正交因素及水平[13]

表4 正交試驗設計及結果1）

3.2 試驗結果分析

9次試驗模擬結果中以第5組的誤差最小，達到0.57%，相應的水平組合為彈性模量180 GPa、柵絲厚度0.005 mm、柵絲長度4 mm、柵絲間距0.056 mm是當前最好的水平搭配。

將4個因素的平均誤差繪在同一張圖上，如圖6所示。可以看出，敏感柵的彈性模量越小，誤差越小，以彈性模量169 GPa為最好；箔柵厚度越小，誤差越小，以厚度0.003 mm為最好；柵絲長度越長，誤差越小，以柵長4 mm為最佳。柵絲間距為0.28 mm時，誤差最低。

圖6 應變傳遞平均誤差與4個因素關系圖

圖7是4個因素和極差關系圖。由圖7可知各因素對結果影響大小的依次順序是：C>B>A>D，即柵絲長度>柵絲厚度>彈性模量>柵絲間距。

圖7 4個因素與極差關系圖

通過上述分析，推斷出最佳水平組合為A1B1C3D3，即彈性模量169 GPa，柵絲厚度0.003 mm，柵絲長度4 mm，柵絲間距0.28 mm。在9次正交試驗中沒有包含這個水平組合，因此要追加試驗。通過有限元模擬分析，追加最佳水平組合試驗的應變傳遞誤差為0.19%，低于上述9次模擬的最好結果0.57%。

4 結束語

采用正交試驗對電阻應變片敏感柵結構參數進行了組合，探討了其對于應變傳遞誤差的影響，并討論了各因素的影響主次。所建立的三維模型通過有限單元法模擬出的應變傳遞率為99.1%，該模型能正確反映應變片的應變傳遞。得出以下結論：

1）敏感柵的彈性模量和柵絲厚度越小，柵絲長度越長，誤差越小，柵絲間距存在最優值。

2）4個因素對應變傳遞誤差的影響主次的依次順序是柵絲長度>柵絲厚度>彈性模量>柵絲間距。

3）通過實驗分析得出最佳參數組合為彈性模量169 GPa，柵絲厚度0.003 mm，柵絲長度4 mm，柵絲間距0.28 mm，應變傳遞誤差為0.19%。

[1]SUBRAMANYA S B, PRASAD M G A. MEMS and MEMS based strain gauge load cells–A review[C]//Research &Technology in the Coming Decades. IET, 2014.

[2]VADIVUCHEZHIAN K, SUBRAHMANYA K, CHOCKAPPAN N. Finite element modeling of effect of adhesive layer and carrier thickness used for strain gauge mounting[J].Advanced Materials Research, 2015, 1119: 828–832.

[3]SUBRAHMANYA K, VADIVUCHEZHIAN K, CHOCKAPPAN N. Experimental verification of effect of adhesive layer thickness used for strain gauge mounting[J]. Advanced Materials Research, 2015, 1119(3):789–793.

[4]KOOMURLU E, CIHANGIR F, KESIMAL A, et al. Effect of adhesive type on the measurement of modulus of elasticity using electrical resistance strain gauges[J]. Arabian Journal for Science & Engineering, 2016, 41(2):433–441.

[5]ZIKE S, MIKKLSEN L P. Correction of gauge factor for strain gauges used in polymer composite testing[J].Experimental Mechanics, 2014, 54(3):393–403.

[6]ZHOU K, WU Z Y. Strain gauge placement optimization for structural performance assessment[J]. Engineering Structures,2017, 141(15):184–197.

[7]張佳明, 王文瑞, 聶帥. 高溫電阻應變片特性參數標定實驗研究[J]. 中國測試, 2014, 40(5):25–28.

[8]王文瑞, 張佳明, 聶帥. 高溫應變接觸式測量精度影響因素研究[J]. 固體火箭技術, 2015(3):439–444.

[9]王文瑞, 王剛, 胡挺,等. 高溫應變柵絲蠕變對應變測量精度影響與補償[J]. 北京科技大學學報, 2017, 39(1):88–95.

[10]胡玉梅, 張方建, 邵毅敏,等. 應變片敏感柵結構參數對測量精度的影響[J]. 重慶大學學報(自然科學版), 2013,36(12):21–27.

[11]尹福炎. 箔式應變片結構模型與有限元分析[J]. 衡器, 2009,38(5):47–50.

[12]耿漢生. 應變膠性能與應變計的工作特性[J]. 傳感器用技術, 1990(4):43–46.

[13]王彪, 劉騰, 徐敬龍,等. 金屬粘貼式電阻應變計應變傳遞分析[J]. 中國測試, 2016, 42(8):1–6.