基于擴張狀態觀測器的自抗擾滑模導引律

楊 柱， 許 哲， 王雪梅， 趙 回， 王 修

(1. 火箭軍工程大學導彈工程學院，陜西 西安 710025; 2. 96656部隊，北京 102208)

0 引 言

制導律是導彈武器系統的核心技術之一，提高制導準確度能極大提高其殺傷力。目前，比例導引由于其制導性能好和工程實現難度低，在制導領域得到了廣泛的應用。但隨著現代戰爭對制導性能要求的提高，如：考慮自動駕駛儀動態特性、落角約束、攻擊大機動目標、時間約束等，以及在導引過程中導彈、目標、彈目相對運動的不完全建模和導引頭引入的噪聲等，使得很難實現更高準確度的制導[1]。

制導信息缺乏是影響制導準確度的重要因素，特別是在考慮導彈自動駕駛儀動態特性情況下更為明顯[2]。目前，用于估計制導信息的主要方法有：擾動觀測器、狀態觀測器、高增益觀測器、卡爾曼濾波等[3-5]。制導信息估計主要有兩個方面：1）未知的目標機動；2）導彈的動態特性[6]。李雅靜[7]等基于改進的CB觀測器，將目標機動視為馬爾科夫過程，設計了制導信息估計模型，提高了制導準確度。Behnamgol[8]等設計了一種非線性觀測器，用于觀測目標信息，抑制滑模控制的抖振。文獻[6]應用高增益觀測器對視線轉率和目標機動進行了估計，使導引模型得到簡化，提高了導引律的魯棒性。文獻[9]通過擴張狀態觀測器(extended state observer, ESO)實時估計目標機動，考慮實際系統中的量測噪聲，設計了一種優于常規方法的導引律。文獻[4]在文獻[9]的基礎上，考慮導彈自動駕駛儀的二階動態特性，設計了一種魯棒性更好的滑模制導律。文獻[10]基于ESO提出了針對機動目標的終端落角約束導引律。以上文獻應用不同的方法實現了對目標機動及其他未知擾動的估計和補償，提高了導引準確度和魯棒性，但均存在某方面的問題，如未考慮導彈動態性能[3, 5, 8-10]，或是沒有考慮導引頭的量測誤差[4, 6-7]，所設計的導引律雖然有其優越性，但對于實際情況考慮仍存在疏漏。

本文應用擴張狀態觀測器實時估計目標機動，對于導引頭的量測誤差，引入了濾波器對輸入進行平滑處理，提高了系統的抗干擾性。考慮導彈的動態特性，提出了一種具有落角約束、過載約束的自抗擾模糊滑模控制導引律。

1 問題描述

本文以縱向平面內的攔截問題為例，將導彈和目標均視為質點，攔截幾何如圖1所示。

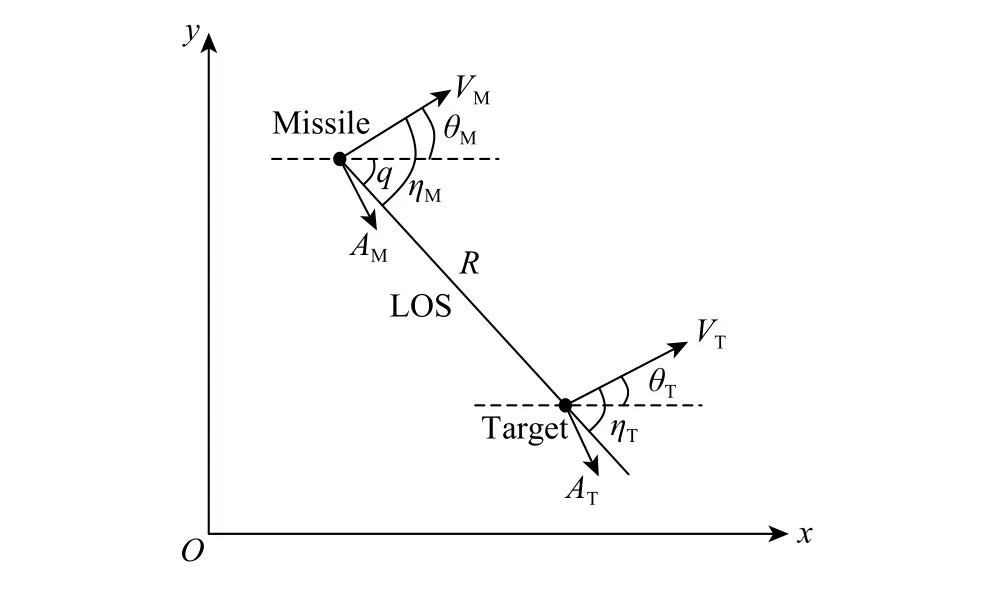
圖1 導彈-目標相對運動關系

其中LOS 為視線，q為 視線角，R為彈目距離，V、A分別為速度和加速度，θ、η分別為縱向平面內的航跡角和視線傾角，下標T和 M分別表示目標參數和導彈參數。

為了便于研究，做如下假設：

1) 導彈可準確測量自身速度和航跡角；

2) 導引頭能測得目標速度和航跡角及彈目視線角，其誤差是有界的；

3) 導彈速度大小恒定，且在整個末制導中均有VM>VT。

參考當前的主被動導引頭資料及實際末制導中導彈主推力一般不存在或不可控，且末制導時間很短，故以上假設合理。

1.1 攔截模型

根據圖1中的彈目攔截幾何關系，可以得出彈目相對運動模型為

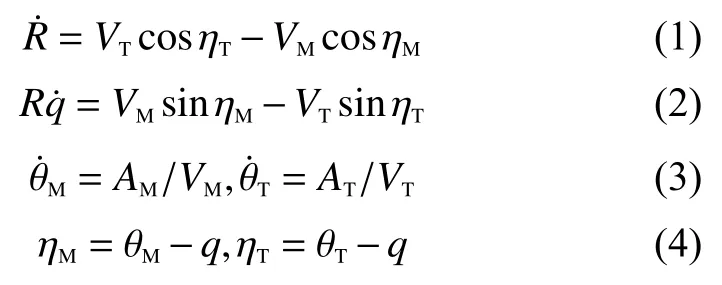
對式(2)求導可得：

其中，和分別表示導彈和目標加速度在視線法向的分量。

基于零化視線角速率的策略，控制導彈對目標的攔截，即q˙→0。

選取適當的控制量，使得導引過程中的彈目實現角速率在有限時間內趨近于0。

1.2 自動駕駛儀動態特性

導彈自動駕駛儀動態特性是一個復雜的過程，但在末制導過程中，為了便于研究，可以將其近似為一階慣性環節[11]，其表達式為

其中，為導彈自動駕駛儀的時間常數，ac為制導系統的制導指令。

1.3 終端落角約束

為了便于表述，定義終端落角為命中點處導彈速度矢量和目標速度矢量的夾角。在的條件下，由式(2)可得：

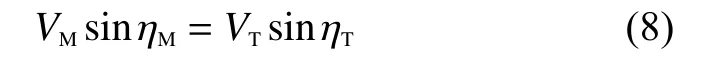
考慮命中點處的幾何關系，可推導命中點處的期望彈目視線角和終端落角的關系為

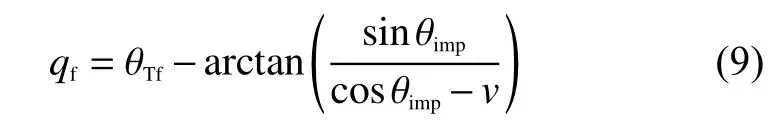
其中，qf為命中點處的期望視線角，θimp為終端落角。由式(9)便可將終端落角約束的問題，轉化為對視線角的控制問題。

2 基于ESO的模糊滑模導引律設計

2.1 模糊滑模導引律

根據上節選擇的制導策略，同時考慮落角約束，參考Li等[12]提出的方法，選取狀態變量控制變量則系統狀態方程為

分別選擇滑模函數和趨近律函數如下：

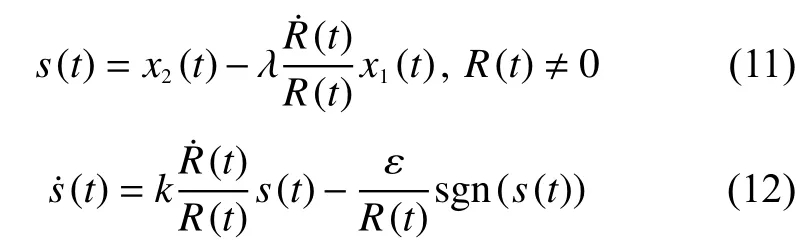
其中，和是正常量，是的符號函數，為趨近率系數，是一個適當的正常量。其穩定性在文獻[12]中已經證明。

由選取的滑模面和趨近律，可得滑模制導律為

其中，AD表示目標機動及模型的不確定性引起的誤差。在導引過程中，彈目距離變化率一般變化很小，可以忽略；而目標機動未知，將Ad視為未知有界干擾。則Ac可以簡化為

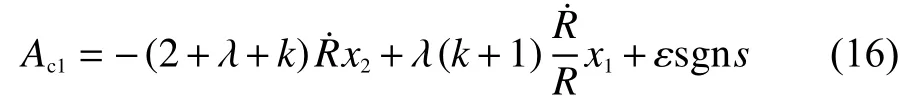
上式中包含符號項εsgns會使系統發生抖振，文獻[12]通過引入自適應神經模糊推理系統(adaptive neural fuzzy inference system, ANFIS)，依靠其強大的自主學習能力，在線計算附加控制指令，減小抖振提高系統魯棒性。所設計的帶有落角約束的魯棒導引律為

其中為ANFIS系統的修正指令。

將滑模面及其一階導數作為神經網絡的輸入有網絡輸出的絕對值為參數項即

其中，為網絡的權值，h(x)為高斯函數。

定義網絡權值調整指標為則由梯度下降法可得

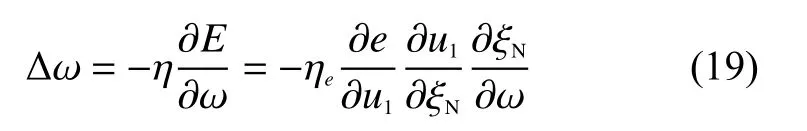
ANFIS系統的修正指令為

代入式(17)可得自適應神經模糊滑模導引律為

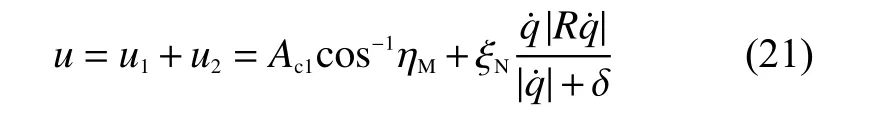
注意到該導引律中包含有AD，若將其視為未知干擾，也能實現理想條件下多約束導引，但在考慮自動駕駛儀動態特性和導引頭量測噪聲后，隨著目標機動的提高，脫靶量急劇增大。主要原因是目標機動帶來的誤差在導彈接近目標的過程中不斷增大。

2.2 ESO設計

通過引入擴張狀態觀測器，能在不考慮目標機動模型的前提下，實現對目標機動的實時估計，即可通過制導指令實時補償，提高導引性能。

將式(10)中的未知項Ad擴張為一個新的狀態，構造系統狀態如下：也是未知的。該系統結構為

對式(22)設計一種二階ESO，其形式為

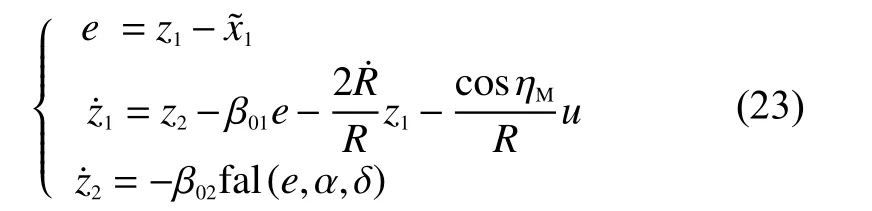
其中，為ESO對系統狀態的觀測誤差，分別為ESO對式(22)的狀態觀測值，為ESO觀測系數，其大小影響ESO的觀測速度和誤差。

由以上ESO可以得到對式(10)的狀態觀測值，只要是有界的，就能通過選擇合適的ESO系數，使得觀測誤差足夠小。當時，有：

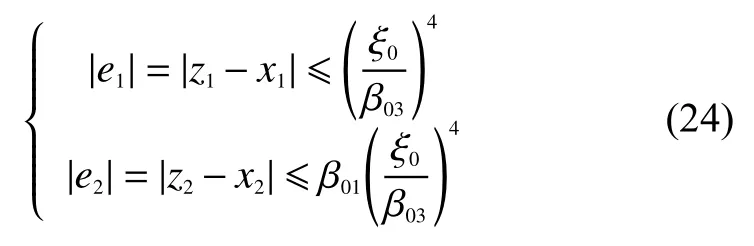
所設計的自抗擾模糊滑模導引律可以表示為

2.3 帶有濾波器的ESO導引律設計

在實際制導過程中，導引頭測量信息必然含有量測噪聲。在式(22)中，由于和一 般數值較大，信噪比相對較小，且從包含和項 中不難看出，其噪聲對導引律影響較小。而的 噪聲相對信噪比較大，且包含的項中有較大的乘積系數，故而對于制導指令影響非常大。令的 量測噪聲為，則式(22)中的變為

設計濾波器對進行估計：

采用濾波后的信號作為ESO的輸入，可以削弱導引頭量測噪聲對觀測效果的干擾，得到較為準確的狀態估值，但同時也會導致觀測結果滯后[13]。為了提高觀測器性能，重新設計濾波擴張狀態觀測器(FESO)，其結構為

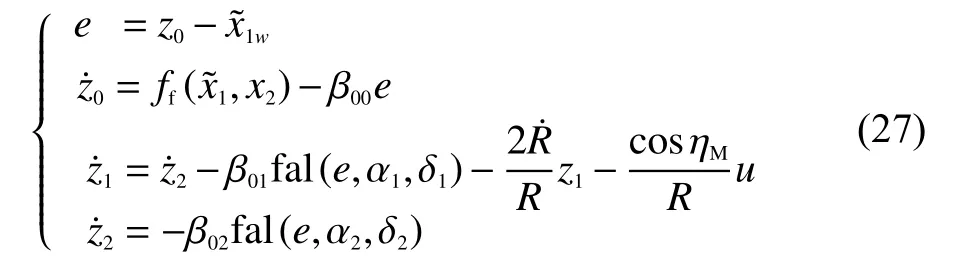
由于是結構可知的濾波器，故可以在ESO中引入濾波方程。所設計的FESO采用濾波結果為輸入，消除了量測噪聲對觀測器的影響。同時，FESO中包含濾波方程，可以避免引入新的觀測誤差。

3 仿真校驗

為了驗證所設計導引律的有效性，考慮兩種情況：1)不考慮噪聲情況下，自適應模糊滑模導引律(ANFSMC)[14]與本文的自抗擾模糊滑模導引律(EFSMC)；2)考慮噪聲干擾后，EFSMC與帶濾波器的自抗擾模糊滑模導引律(FEFSMC)。

仿真參數設置如下，導彈初始坐標為(0, 10000)，初始航向角為-60°，速度為900m/s，最大過載為10g，自動駕駛儀時間常數τ=0.15，目標初始坐標(1000, 0)，初始航向角為0°，速度為，目標機動信號為：AT=50×sinπt+20，落角約束要求為90°，導彈最大可用過載，導引律盲區范圍df=50m。

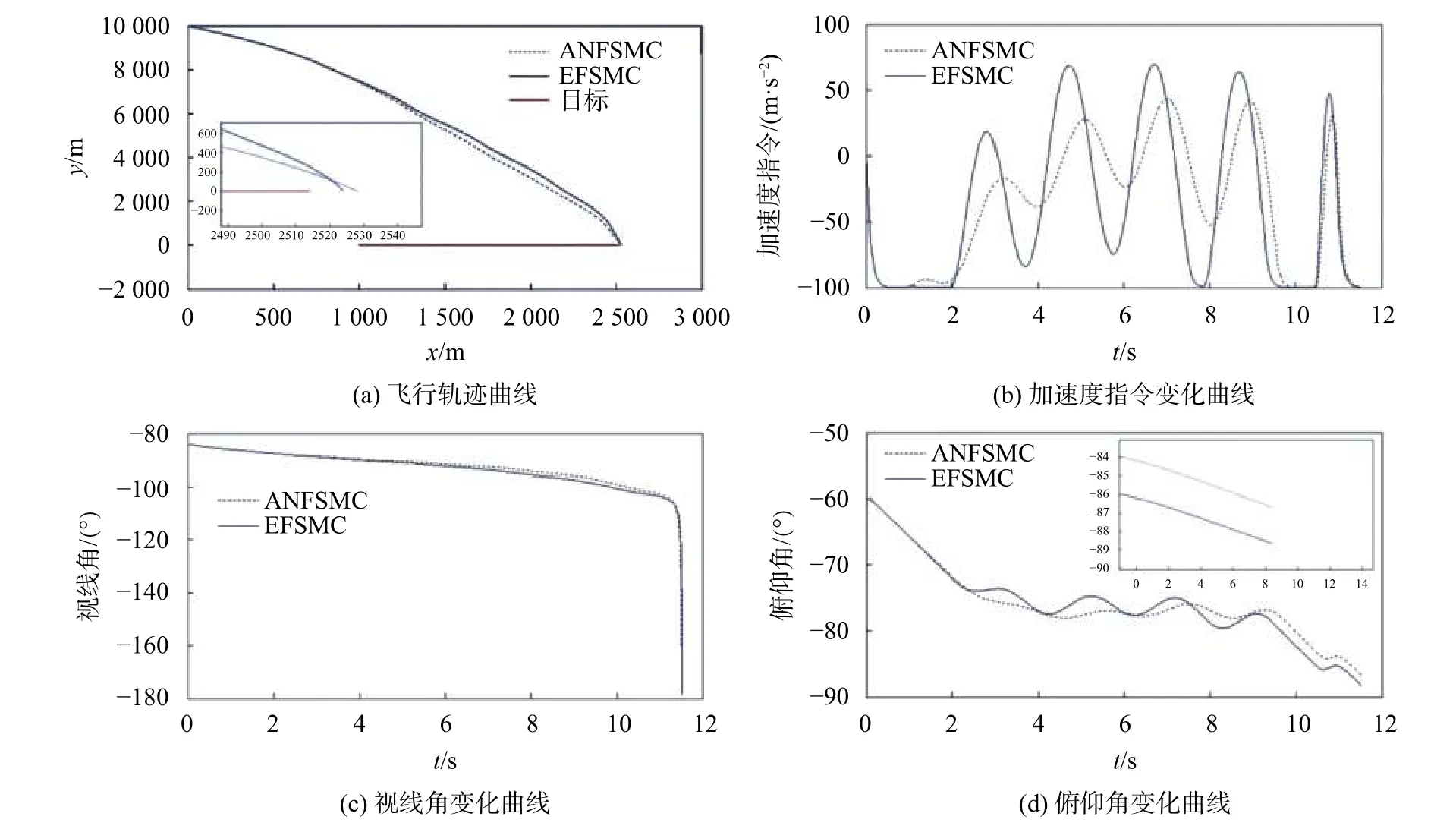
圖2 ANFSMC與EFSMC對比結果

3.1 EFSMC性能仿真

ANFSMC導引律參數選擇如下：k=1.8，λ=1.5，ε=50，σ=0.01。ESO參數選擇為：β01=20，β02=40，α=0.5，δ=0.01。仿真結果如圖2所示，兩種導引律均能命中目標，但從圖2(b)可知，EFSMC在末制導中段的加速度指令比ANFSMC大，這是因為將ESO觀測到的目標加速度附加到了加速度指令中，這樣能更好地利用導彈在中段的機動能力，使導彈在攔截點處的脫靶量和落角誤差更小，在圖2(d)中可以明顯看到。

ESO對于目標加速度的跟蹤情況如圖3所示，由圖可知，在剛開始觀測時觀測值有較大誤差，雖然可以通過調整觀測器參數將其減小，但相應地會導致ESO跟蹤性能下降，動態特性降低，使導引效果變差。綜合考慮ESO的觀測性能和導引律不出現較大突變，在設計的導引中，開始階段（本文考慮開始的0.5 s內）不引入觀測器結果。從圖3可看出ESO的觀測效果非常準確，穩態誤差在0.3g以內，只是在觀測的最后階段出現了偏離。這是由于在攔截點附近，彈目視線角速率會出現非常大的波動，極大地影響觀測效果。在實際情況中，這也是不可避免的，但時間非常短，故而對于導引結果影響很小。

情況1詳細的仿真結果如表1所示，由表可知，相比于ANFSMC，EFSMC的脫靶量更小，落角也更為精確。

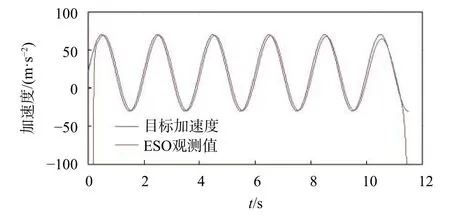
圖3 ESO觀測結果

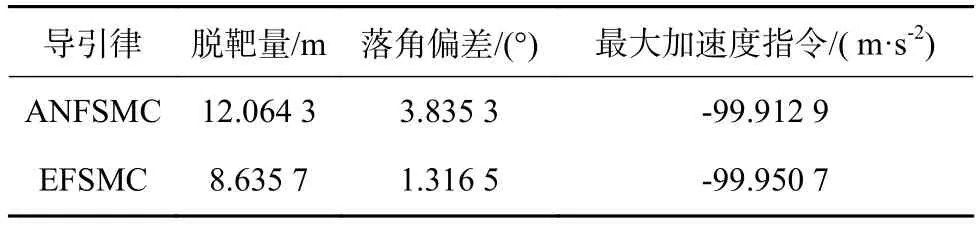
表1 情況1詳細結果

3.2 FEFSMC性能仿真

對于EFSMC導引律參數選擇與情況1相同。FEFSMC中觀測參數選擇為：β00=70，β01=50,β02=170,α1=0.5,α2=0.25，δ=0.01，濾波器選用一階低通濾波器。的量測噪聲采用零均值，均方根為1×10?4的高斯白噪聲。仿真結果如圖4所示，兩種導引律都能實現落角約束的精確導引。但由于噪聲的影響，EFSMC對于目標加速度的觀測出現了抖振，導致加速度指令也出現抖振，會極大地影響導彈控制系統的穩定性，而FEFSMC導引準確度更高，落角偏差更小。

圖4 FEFSMC與EFSMC對比結果

目標加速度的觀測如圖5所示，圖5(a)為ESO對目標加速度觀測值，圖5(b)為FESO的觀測值，對比看出，FESO對噪聲的抗干擾性更強，觀測值接近真實值，穩態誤差在1g以內。另外也可從圖5(a)中看出，ESO的觀測誤差隨時間而減小，這是因為ESO本身就是一種自抗擾觀測器。可以通過調整ESO參數削弱噪聲的影響，或者直接將濾波結果引入觀測器，不過這都會導致觀測滯后[13]。

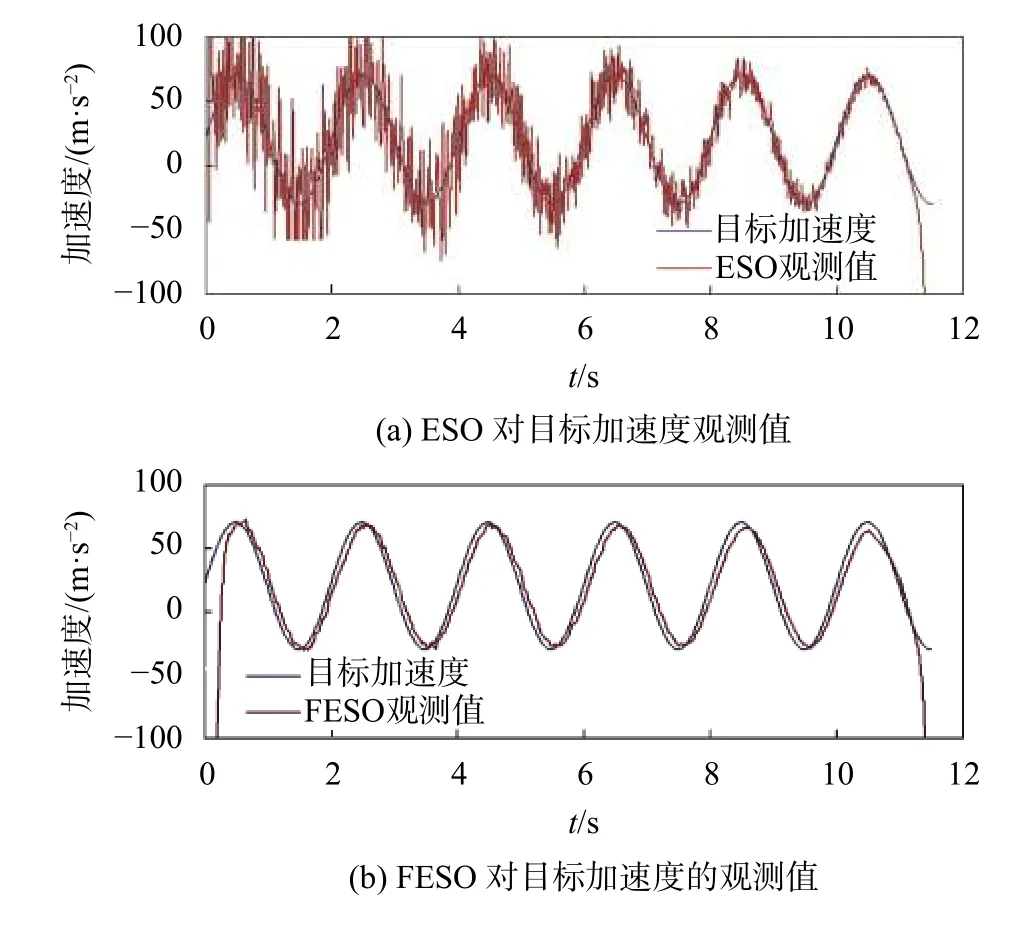
圖5 對目標加速度的觀測結果

4 結束語

通過理論分析和仿真實驗驗證了本文所提算法的有效性，主要結論總結如下：

1) 基于ANFSMC改進的EFSMC能夠實現落角約束下針對大機動目標的精確導引，在不考慮量測噪聲的情況下，脫靶量和落角偏差均較小。

2) ESO對于本研究中的目標機動能準確觀測，在無噪聲情況下的穩態誤差小于0.3g；考慮噪聲后，改進的FESO穩態誤差小于1g，而ESO則存在較大振動。

3) 考慮噪聲后，改進的FEFSMC相比EFSMC脫靶量和落角偏差更小，加速度指令更平滑。

[1]劉興堂. 導彈制導控制系統分析、設計與仿真[M]. 西安: 西北工業大學出版社, 2006: 4–6.

[2]ZHOU D, XU B. Adaptive dynamic surface guidance law with input saturation constraint and autopilot dynamics[J]. Journal of Guidance, Control, and Dynamic, 2016, 39(5): 1155–1162.

[3]王曉芳, 鄭藝裕, 林 海. 基于擾動觀測器的終端角約束滑模導引律[J]. 系統工程與電子技術, 2014, 36(1): 111–116.

[4]張堯, 郭杰, 唐勝景,等. 基于擴張狀態觀測器的導彈滑模制導律[J]. 北京航空航天大學學報, 2015, 41 (2): 343–350.

[5]曹有亮, 張金鵬. 擴展卡爾曼濾波的目標機動信息估計研究[J].航空兵器, 2016, 41 (1): 40–44.

[6]馬克茂, 馬杰. 機動目標攔截的變結構制導律設計與實現[J].宇航學報, 2010, 31(6): 1589–1593.

[7]李雅靜, 侯明善, 熊飛. 一種改進的觀測器算法在制導中的應用[J]. 宇航學報, 2010, 31(8): 1920–1926.

[8]BEHNAMGOL V, VALI A R, MOHAMMADI A. A new observer–based chattering–free sliding mode guidance law[J].Journal of Aerospace Engineering. 2016, 230(8): 1489–1495.

[9]姚郁, 王宇航. 基于擴張狀態觀測器的機動目標加速度估計[J].系統工程與電子技術, 2009, 31(11): 2682–2684.

[10]XIONG S F, WANG W H, SONG S Y, et al. Extended state observer based impact angle constrained guidance law for maneuvering target interception[J]. Journal of Aerospace Engineering, 2015, 229(14): 2589–2607.

[11]周衛東, 陳沿逵, 熊少鋒. 帶有攻擊角約束的無抖振滑模制導律設計[J]. 北京航空航天大學學報, 2016, 42 (4): 669–676.

[12]LI Q C, ZHANG W S, HAN G, et al. Adaptive neuro–fuzzy sliding mode control guidance law with impact angle constraint [J]. IET Control Theory and Applications, 2015, 9(14): 2115–2123.

[13]林飛, 孫湖, 鄭瓊林, 等. 用于帶有量測噪聲系統的新型擴張狀態觀測器[J]. 控制理論與應用, 2005, 22(6): 995–998.

[14]ZHOU D, SUN S. Guidance laws with finite time convergence[J]. Journal of Guidance, Control, and Dynamics,2009, 32(6): 1838–1846.