基于壓重塊型TMD的大跨度斜拉橋減震控制

王 浩， 鄒仲欽， 茅建校， 陶天友

(東南大學(xué)混凝土及預(yù)應(yīng)力混凝土結(jié)構(gòu)教育部重點(diǎn)實(shí)驗(yàn)室， 江蘇 南京 210096)

引 言

隨著中國經(jīng)濟(jì)水平的提高，交通事業(yè)也蓬勃發(fā)展，近年來興建了一系列跨江、跨海的大跨度橋梁，如潤揚(yáng)大橋、蘇通大橋、杭州灣大橋等[1]。目前，世界上已有不少大跨度橋梁遭受地震破壞的實(shí)例[2]，如1995年日本神戶大橋在神戶地震中遭受破壞、1989年舊金山奧克蘭灣大橋東跨的懸臂桁架在洛馬·普雷塔大地震中倒塌；1999年集集大橋主梁和主塔在集集大地震中破壞等。大跨度橋梁作為重要的生命線工程，如何保證其抗震安全性顯然十分重要，而如何對其地震響應(yīng)進(jìn)行有效控制也一直是橋梁工程界研究的熱點(diǎn)問題之一[2]。

在橋梁結(jié)構(gòu)減震控制方法及控制裝置方面，近年來已取得了一系列富有成效的研究成果。而在眾多可供選擇的控制裝置中，質(zhì)量阻尼器(例如TMD和ATMD)是最常用的裝置[3]。TMD是由一個質(zhì)量塊、彈簧和阻尼器組成的系統(tǒng)，可以持續(xù)提供一種與主結(jié)構(gòu)運(yùn)動方向相反的慣性力，以減小結(jié)構(gòu)的動力響應(yīng)。國內(nèi)外有許多高聳結(jié)構(gòu)安裝了TMD來控制結(jié)構(gòu)的振動，例如，中國臺北的101大樓在87～92層間設(shè)置了球形質(zhì)量塊并輔以8對油壓阻尼器，使減震效果達(dá)到了40%[4]；美國芝加哥的凱越酒店，采用了質(zhì)量塊為300 t的TMD系統(tǒng)來減少結(jié)構(gòu)的振動響應(yīng)[5]。在橋梁工程中，中國九江長江大橋使用了TMD系統(tǒng)來抑制吊桿的渦振[6]；徐剛等[7]研究了TMD系統(tǒng)對施工中大橋橋塔的減振性能影響；樊健生等[8]研究了人行橋的TMD減振優(yōu)化設(shè)計(jì)。但由于TMD的設(shè)置將顯著增大橋梁結(jié)構(gòu)的恒載，使其在實(shí)際工程中的應(yīng)用受到限制[9]。

對于邊主跨比相對較小的斜拉橋，常常通過在邊跨設(shè)置壓重塊來平衡主跨重力，若將此類斜拉橋的壓重塊與鋼箱梁間采用彈簧和阻尼裝置連接，改裝成為壓重塊型TMD，則可在保持壓重塊功能的同時，既不增大結(jié)構(gòu)的恒載，又發(fā)揮TMD的結(jié)構(gòu)減振功能[10]。為此，本文參照蘇通大橋結(jié)構(gòu)，分別建立了有/無輔助墩的兩種大跨度斜拉橋的有限元模型，對比分析了大跨橋梁在地震動作用下的結(jié)構(gòu)響應(yīng)，再將邊跨的壓重塊等效為TMD中的質(zhì)量塊，設(shè)計(jì)改裝成壓重塊型TMD，并將采用壓重塊型TMD前后大跨度斜拉橋的地震響應(yīng)進(jìn)行了對比分析，為今后大跨度斜拉橋的減震控制研究提供了新思路，同時為未來大跨度斜拉橋壓重塊型TMD的設(shè)計(jì)與改裝提供了參考。

1 大跨度斜拉橋壓重塊型TMD設(shè)計(jì)

蘇通大橋?yàn)殡p索面鋼箱梁斜拉橋，采用扁平流線型閉口鋼箱梁，中心處梁高4 m，含風(fēng)嘴在內(nèi)寬41 m，索塔總高為300.4 m，最長斜拉索長度為577 m，全橋共272根斜拉索，塔柱為單箱單室倒Y形截面，為了平衡主跨的自重以減小主塔的縱向彎曲和主跨下?lián)希趦蓚€邊跨分別安裝有鐵塊作為壓重塊[11]。本節(jié)通過對壓重塊進(jìn)行全新改裝，據(jù)此設(shè)計(jì)出一種新型的壓重塊型TMD，以在確保壓重功能的同時，起到減小結(jié)構(gòu)的地震響應(yīng)的作用。

1.1 結(jié)構(gòu)有限元模型的建立

本文以蘇通大橋?yàn)榻Y(jié)構(gòu)原型，設(shè)計(jì)了兩座跨徑分別為(100+100+300+1088+300+100+100) m和(500+1088+500) m的大跨度斜拉橋(如表1所示)，兩橋的主要區(qū)別在于邊跨是否設(shè)有輔助墩。基于ANSYS建立了兩種橋型的有限元模型，如圖1所示。在該空間模型中，將橫梁、加勁梁、索塔和橋墩簡化為梁單元，用Beam4單元模擬，其中按斜拉索的吊點(diǎn)進(jìn)行加勁梁的離散；將斜拉索簡化成索單元，用Link10單元模擬，拉索的自重垂度效應(yīng)采用Ernst方法修正彈性模量來考慮[12]，同時斜拉索軸力對剛度的影響采用應(yīng)力剛化方法添加幾何剛度矩陣來考慮[13]。耦合主梁與主塔在橫橋向及繞順橋向的轉(zhuǎn)動自由度，以及主梁與橋墩在豎向和橫向自由度，并將橋墩和主塔底部完全固結(jié)，不考慮土-樁-結(jié)構(gòu)相互作用。

表1 兩種橋型的結(jié)構(gòu)形式對比

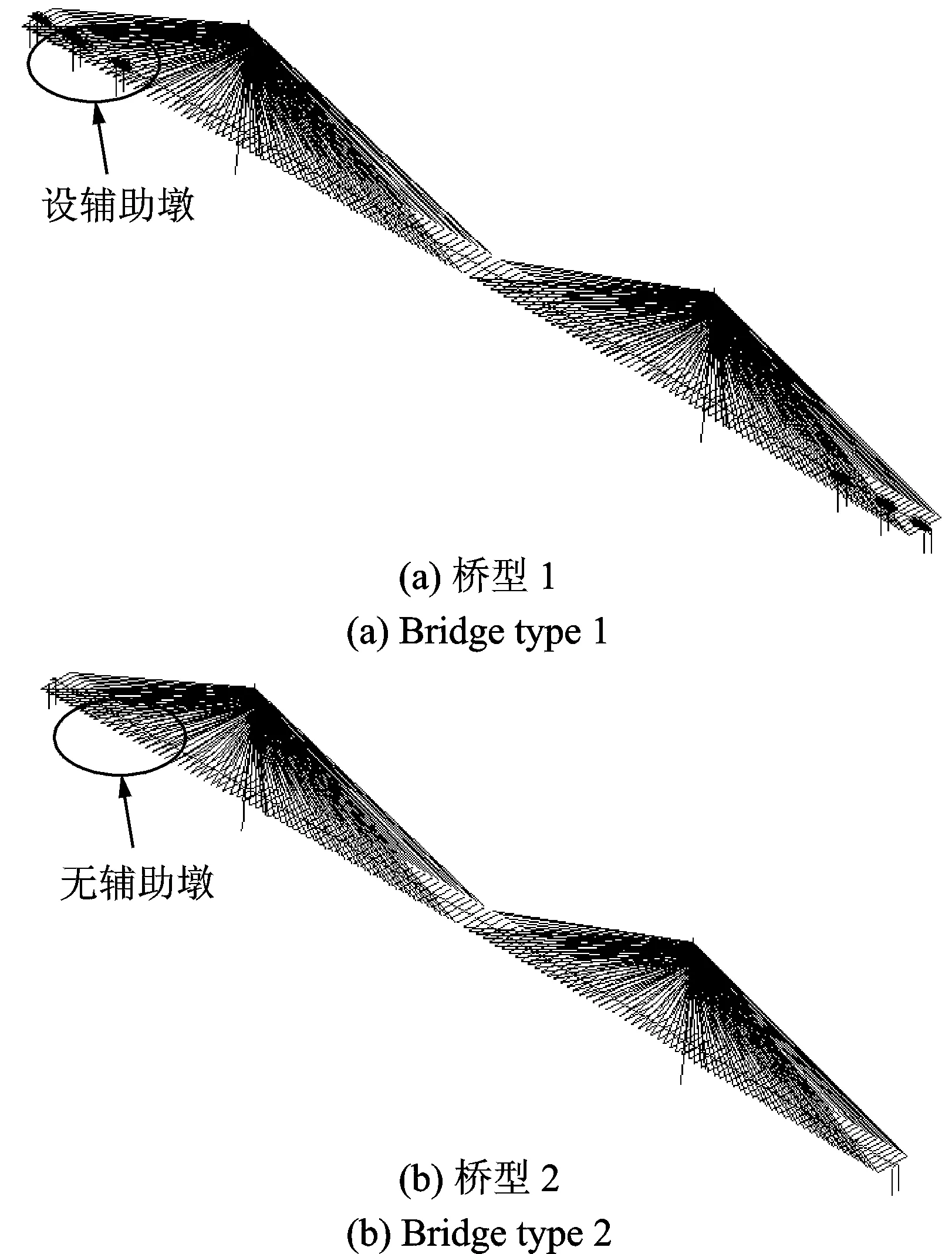
圖1 大跨度斜拉橋空間有限元計(jì)算模型
Fig.1 Finite element model of the long-span cable-stayed bridges

1.2 壓重塊型TMD的改裝設(shè)計(jì)

TMD是由一個質(zhì)量塊、彈簧和阻尼器組成的系統(tǒng)。將它與主結(jié)構(gòu)相連并進(jìn)行適當(dāng)?shù)恼{(diào)整，由于通過彈簧的連接，可以持續(xù)提供一種和主結(jié)構(gòu)的運(yùn)動方向相反的慣性力，以減小結(jié)構(gòu)的動力響應(yīng)。本課題組在前期工作中已對壓重塊型TMD用于鋼箱梁風(fēng)振控制的效果進(jìn)行了分析[10]，并已獲得了相應(yīng)的國家發(fā)明專利授權(quán)(專利號：ZL 201110197020.9)，研究結(jié)果表明，壓重塊型TMD可明顯改善大跨度斜拉橋的抖振響應(yīng)。

大跨度斜拉橋帶有壓重塊的鋼箱梁典型截面如圖2(a)所示，壓重塊直接安裝在大跨度斜拉橋的鋼箱梁底板上。顯然可以將壓重塊等效為質(zhì)量塊，用彈簧和阻尼器和上下連接板相連、用橫向限位裝置與隔板相連，并采用高強(qiáng)螺栓與橋面連接，形成一個等效的TMD系統(tǒng)，其質(zhì)量塊可以在平面內(nèi)與鋼箱梁產(chǎn)生豎向相對位移，而不產(chǎn)生橫向相對位移，如圖2(b)所示。其中等效質(zhì)量塊應(yīng)對稱分布在鋼箱梁中心線兩側(cè)，遠(yuǎn)離對稱軸放置，以增強(qiáng)對大橋側(cè)彎和扭轉(zhuǎn)振動的控制效果。

圖2 大跨度斜拉橋的橫截面形式
Fig.2 The cross-sections of steel box girder of the long-span cable-stayed bridges

通過ANSYS中的Mass21單元將質(zhì)量塊簡化為獨(dú)立的質(zhì)量，沿縱軸線對稱布置。彈簧和阻尼器均采用ANSYS的Combin14單元來模擬。

2 大跨度斜拉橋地震響應(yīng)分析

2.1 動力特性分析

采用子空間迭代法分別計(jì)算了兩種橋型的前300階模態(tài)頻率和振型。其中兩種橋型的前10階模態(tài)頻率和振型對比如表2所示，圖3為橋型1的一些典型的振型。

表2 大跨度斜拉橋前10階模態(tài)

Tab.2 The first ten modes and frequencies of the long-span cable-stayed bridges

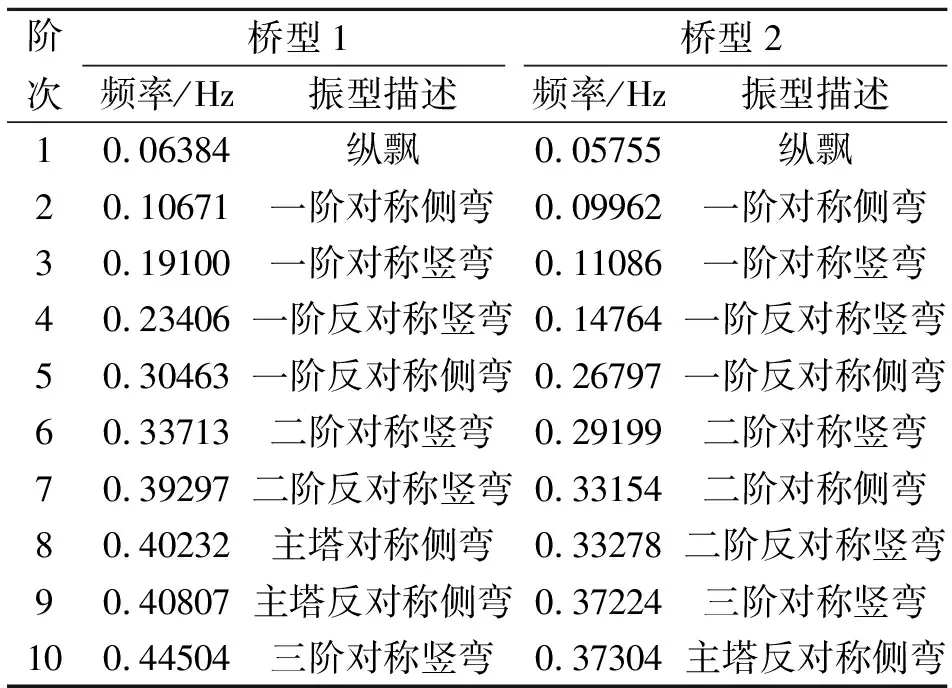
階次橋型1橋型2頻率/Hz振型描述頻率/Hz振型描述10.06384縱飄0.05755縱飄20.10671一階對稱側(cè)彎0.09962一階對稱側(cè)彎30.19100一階對稱豎彎0.11086一階對稱豎彎40.23406一階反對稱豎彎0.14764一階反對稱豎彎50.30463一階反對稱側(cè)彎0.26797一階反對稱側(cè)彎60.33713二階對稱豎彎0.29199二階對稱豎彎70.39297二階反對稱豎彎0.33154二階對稱側(cè)彎80.40232主塔對稱側(cè)彎0.33278二階反對稱豎彎90.40807主塔反對稱側(cè)彎0.37224三階對稱豎彎100.44504三階對稱豎彎0.37304主塔反對稱側(cè)彎

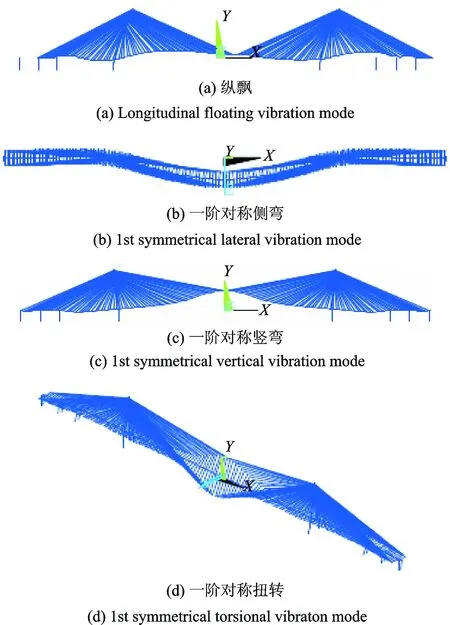
圖3 大跨度斜拉橋的一些典型振動模態(tài)
Fig.3 Some typical vibration modes of the long-span cable-stayed bridge

表1和圖3表明，兩種橋型的振型接近，但橋型1的模態(tài)頻率較橋型2更大，說明輔助墩的存在可以有效提高結(jié)構(gòu)的整體剛度。與橋型2類似，橋型1的第1階模態(tài)的基本周期較長，為15.773 s，對應(yīng)振型為主梁縱飄，與該橋?yàn)槠◇w系相符；第2階模態(tài)頻率為0.10671 Hz，對應(yīng)振型為主梁一階對稱側(cè)彎，第3階模態(tài)頻率為0.19100 Hz，對應(yīng)振型為主梁一階對稱豎彎，該橋的豎彎模態(tài)晚于側(cè)彎模態(tài)出現(xiàn)，是因?yàn)榕c一般的斜拉橋而相比該橋的寬跨比更小；主塔對稱側(cè)彎振型出現(xiàn)在第8階，其對應(yīng)的振動頻率為0.40232 Hz，主塔反對稱側(cè)彎振型出現(xiàn)在第9階，其對應(yīng)的振動頻率0.40807 Hz，與大跨度斜拉橋自振特性的一般規(guī)律相符合[14]。

2.2 地震響應(yīng)分析

選擇常用的Tianjin波、El Centro波和Taft波作為輸入的地震動波，并根據(jù)《公路橋梁抗震設(shè)計(jì)細(xì)則》[15]，將三條波的加速度峰值調(diào)整為0.15g，豎向地震波取為相應(yīng)的水平地震波的1/2。

采用子空間迭代法分別計(jì)算兩種橋型在三種地震波、分別采用橫向、縱向、豎向、橫向+豎向和縱向+豎向輸入下的地震響應(yīng)，計(jì)算結(jié)果表明，兩種橋型的響應(yīng)規(guī)律近似，在縱向+豎向地震輸入下橋梁結(jié)構(gòu)的響應(yīng)均最大，該工況下橋型1的關(guān)鍵位置響應(yīng)結(jié)果如表3所示。且由表3可知，結(jié)構(gòu)在Tianjin波下的響應(yīng)最大，因此本文只選取了Tianjin波進(jìn)行分析，地震波采取縱向+豎向輸入方式。

在Tianjin波縱向+豎向輸入下，該橋主要是豎向和縱向模態(tài)被激發(fā)，故本文主要選取結(jié)構(gòu)的豎向時程響應(yīng)進(jìn)行分析。其中設(shè)輔助墩橋在主跨跨中、主跨L/4處以及邊跨跨中的豎向位移和加速度時程分別如圖4(a)～(f)所示。

由圖4可知，地震作用下結(jié)構(gòu)整體豎向位移響應(yīng)并不大，最大振幅也在0.5 m以內(nèi)，對于主跨為1088 m的斜拉橋而言是可以接受的；但結(jié)構(gòu)豎向加速度響應(yīng)較大，在主跨L/4處的豎向加速度峰值甚至達(dá)到了7.45 m/s2，與橋型1類似，橋型2同樣在主跨L/4處的豎向加速度響應(yīng)也較大，其峰值達(dá)到了6.21 m/s2。由于過大的結(jié)構(gòu)振動加速度會嚴(yán)重影響到大橋的行車舒適度和運(yùn)營安全性， 故本文TMD系統(tǒng)主要以控制主跨L/4處的加速度響應(yīng)為目標(biāo)來進(jìn)行設(shè)計(jì)。

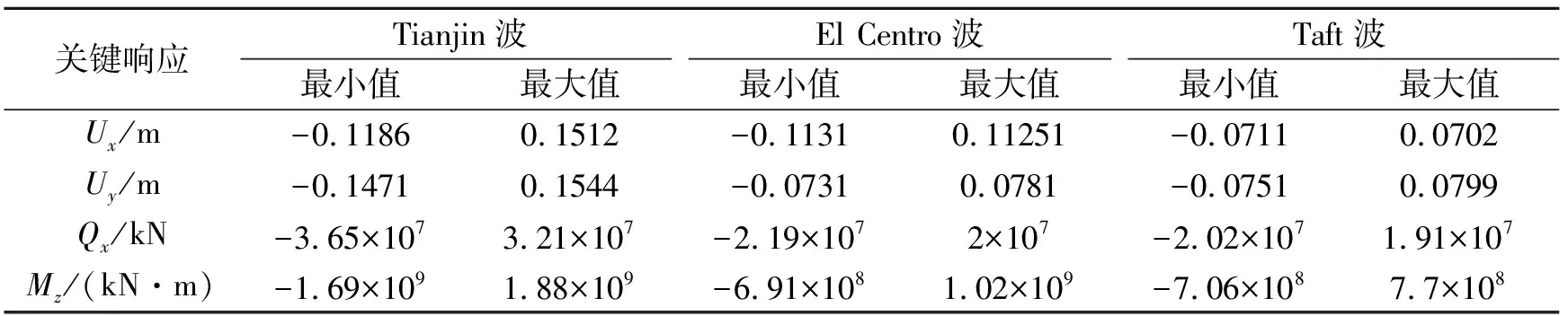
表3 縱向+豎向地震作用下結(jié)構(gòu)關(guān)鍵截面的響應(yīng)

注：Ux：塔頂縱向位移；Uy：跨中豎向位移；Qx：塔底縱向剪力；Mz：塔底縱向彎矩

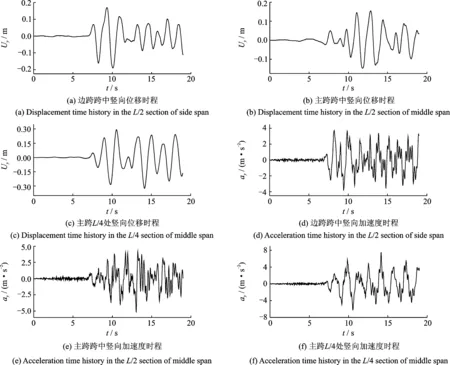
圖4 結(jié)構(gòu)關(guān)鍵截面位移及加速度時程Fig.4 Displacement and acceleration time histories of some key sections

3 壓重塊型TMD減震效果分析

3.1 壓重塊型TMD參數(shù)設(shè)計(jì)

為了能夠?qū)崿F(xiàn)對主跨L/4處加速度響應(yīng)的TMD有效控制，首先進(jìn)行了兩種橋型在主跨L/4處的豎向加速度響應(yīng)的功率譜密度分析，分別如圖5(a)和(b)所示。

由圖5可知，橋型1的功率譜密度峰值出現(xiàn)在0.659 Hz處，因此根據(jù)大橋的動力特性分析結(jié)果，考慮控制大橋的第19階振型，其對應(yīng)的模態(tài)頻率為0.654 Hz，與峰值處頻率接近；同理，橋型2的功率譜峰值在出現(xiàn)在0.708 Hz處，考慮控制結(jié)構(gòu)的26階振型。

各橋墩附近所安裝的TMD參數(shù)如表4所示。表中TMD質(zhì)量均由相應(yīng)的壓重塊質(zhì)量計(jì)算獲得，彈簧剛度和阻尼系數(shù)通過TMD的參數(shù)優(yōu)化得到。其中橋型1在控制模態(tài)下的質(zhì)量比為0.3088，橋型2對應(yīng)的質(zhì)量比為0.122。

表4 TMD的參數(shù)

圖5 主跨L/4處豎向加速度功率譜密度
Fig.5 Power spectral density of vertical acceleration in the L/4 section of middle span

3.2 TMD減震效果對比分析

采用壓重塊型TMD前后，橋型1主跨L/4處的豎向加速度時程及其功率譜密度對比分別如圖6(a)和(b)所示；采用壓重塊型TMD前后主跨L/4處的豎向加速度時程及其功率譜密度對比分別如圖6(c)和(d)所示。

從圖中可知，橋型1采用壓重塊型TMD后豎向加速度時程峰值為6.06 m/s2，仍然較大。TMD雖然對某些時刻的豎向加速度存在一定的減震效果，但總體而言并沒有明顯的改善，對功率譜峰值也有一定程度的降低，但并沒有達(dá)到理想的減震效果；而橋型2采用壓重塊型TMD后豎向加速度時程峰值為5.30 m/s2，減震率達(dá)到21%，由功率譜密度也可知，TMD系統(tǒng)有效降低了功率譜峰值，減震效果明顯。原因是當(dāng)TMD安裝在輔助墩附近時，質(zhì)量塊的自由振動會受到限制，因此影響了TMD的減震效果。

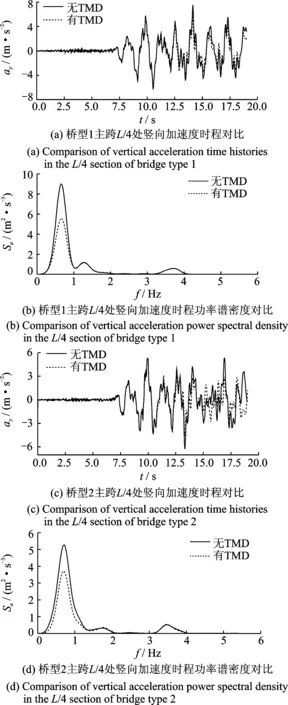
圖6 采用壓重塊型TMD前后加速度性能對比
Fig.6 Comparison of acceleration performance of the bridge types with and without TMDs

對于橋型2，即在無輔助墩情況下，壓重塊型TMD對主梁其他位置依然有很好的控制效果。采用壓重塊型TMD前后橋型2各位置地震響應(yīng)峰值對比如表5以及圖7～9所示。

表5 采用壓重塊型TMD前后橋型2各關(guān)鍵截面地震響應(yīng)峰值對比

Tab.5 Comparison of the peak seismic responses in some key sections of bridge type 2 with and without TMDs

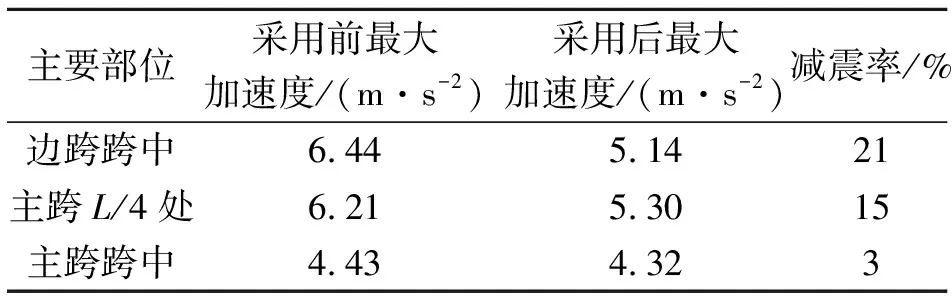
主要部位采用前最大加速度/(m·s-2)采用后最大加速度/(m·s-2)減震率/%邊跨跨中6.445.1421主跨L/4處6.215.3015主跨跨中4.434.323

注：減震率定義為采用前后最大加速度差值與采用前最大加速度的比值

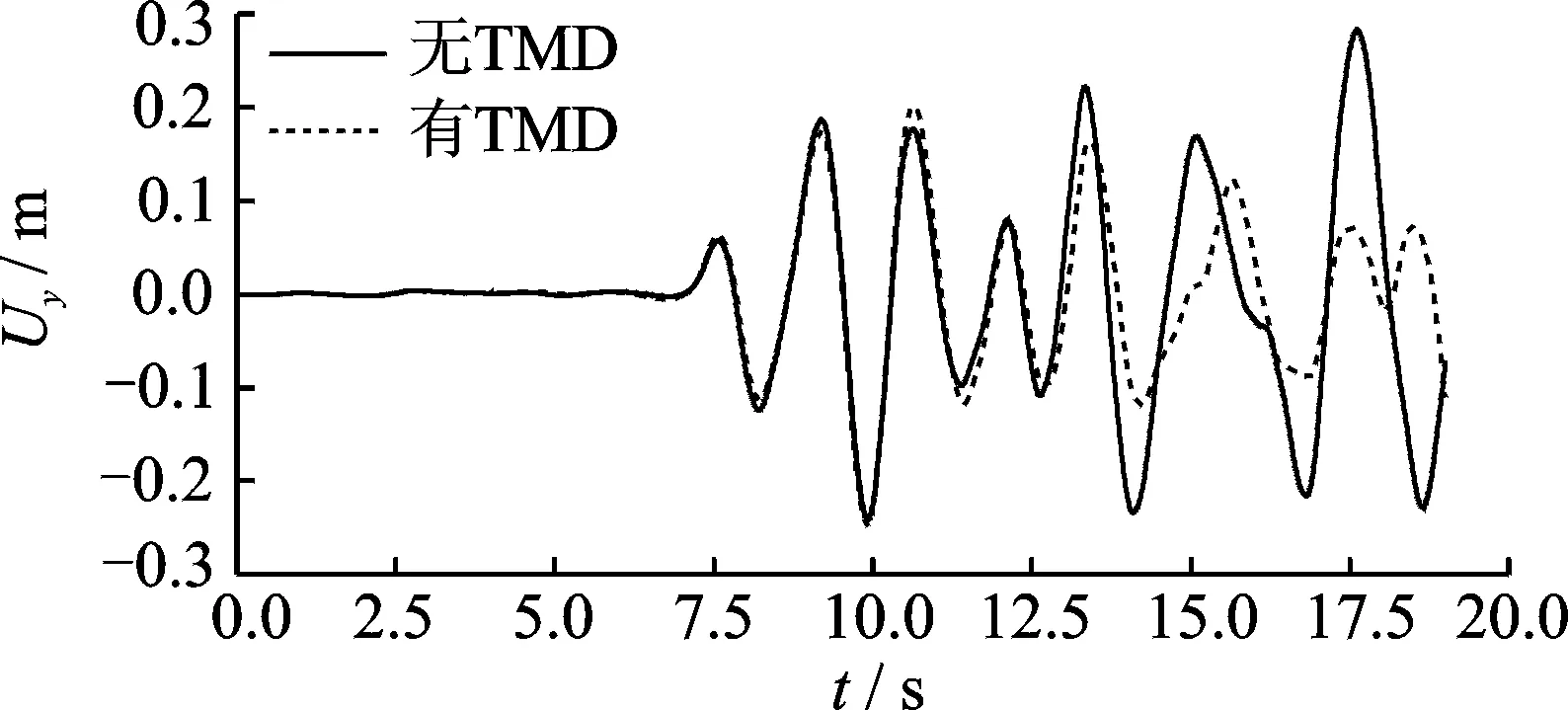
圖7 采用壓重塊型TMD前后主跨L/4處豎向位移時程對比
Fig.7 Comparison of displacement time histories in the L/4 section of the bridge with and without TMDs

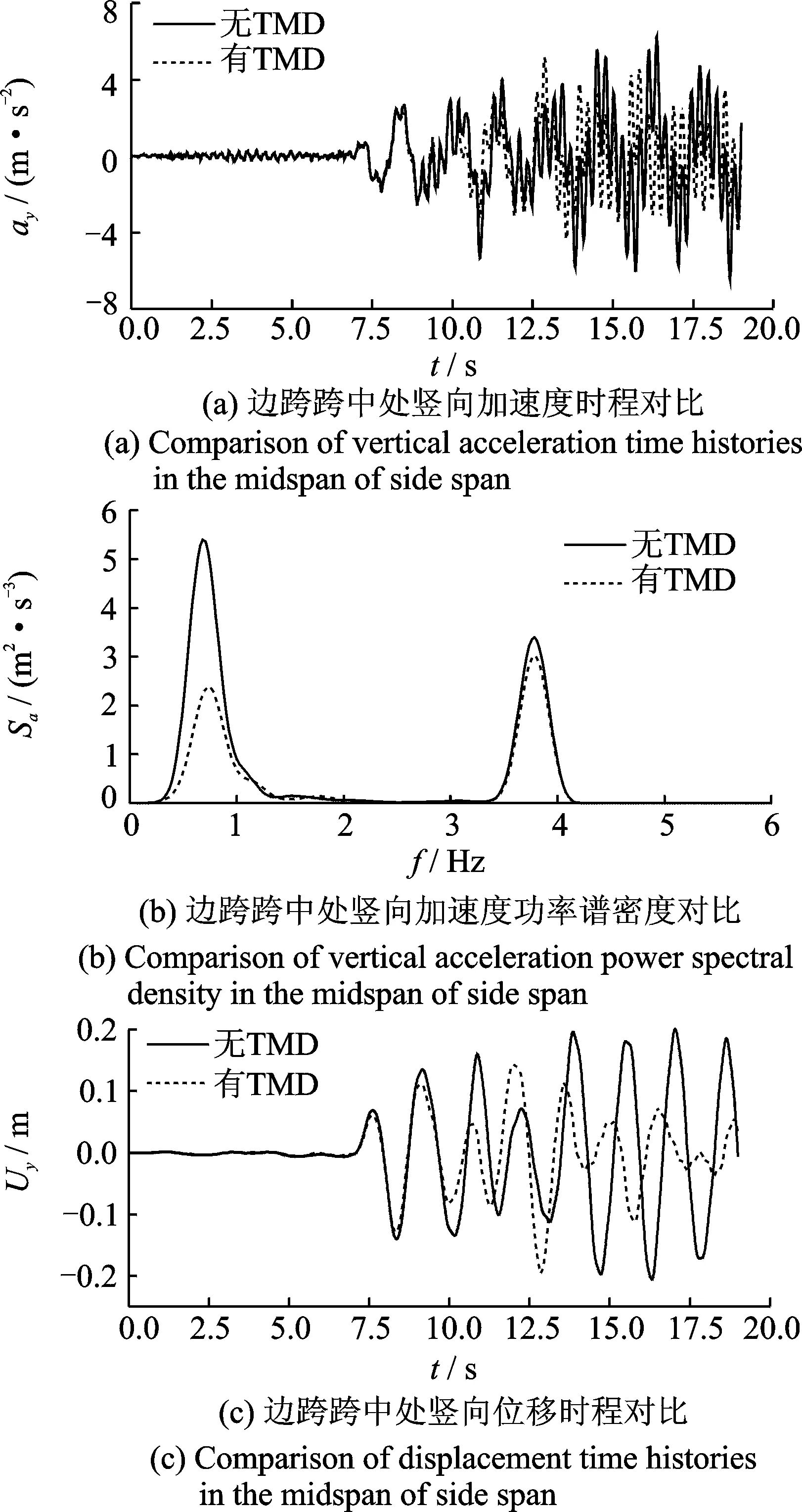
圖8 采用壓重塊型TMD前后邊跨地震響應(yīng)對比
Fig.8 Comparison of seismic responses of the side span with and without TMDs

圖7為采用壓重塊型TMD前后主跨L/4處的豎向位移時程對比，可見所設(shè)計(jì)的壓重塊型TMD不僅能有效控制主跨L/4處的加速度響應(yīng)，對該點(diǎn)的位移響應(yīng)的控制效果同樣顯著。

圖8為采用壓重塊型TMD前后，該橋邊跨跨中豎向加速度時程及其功率譜密度、豎向位移時程對比圖。由圖8可見，所設(shè)計(jì)的壓重塊型TMD對邊跨跨中處加速度響應(yīng)同樣有著良好的控制效果。

采用壓重塊型TMD前后，主跨跨中的豎向加速度時程及其功率譜密度、豎向位移時程對比如圖9所示。從圖中可知，壓重塊型TMD對跨中的減震效果不明顯，原因是TMD的控制頻率對應(yīng)的結(jié)構(gòu)振型是振型位移為0的反對稱豎彎，抑制該階振型對結(jié)構(gòu)跨中的位移及加速度基本無影響。

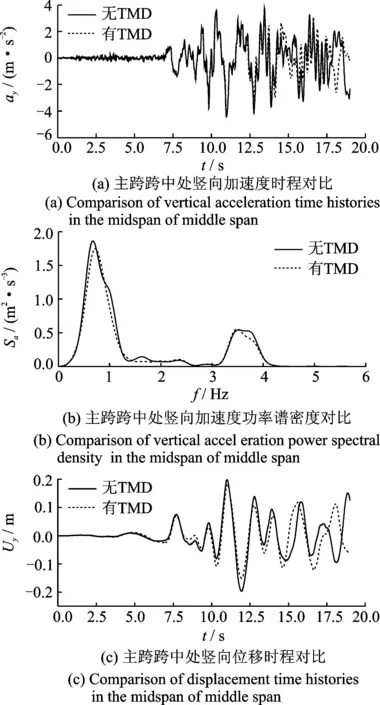
圖9 采用壓重塊型TMD前后主跨地震響應(yīng)對比
Fig.9 Comparison of seismic responses of the main span with and without TMDs

4 結(jié) 論

本文提出了一種基于壓重塊型TMD的大跨度斜拉橋減震控制方法，所得結(jié)論如下：

1) 設(shè)計(jì)的壓重塊型TMD能有效控制大跨度斜拉橋的地震響應(yīng)，在顯著減小結(jié)構(gòu)的加速度及位移時程響應(yīng)的同時，又能保持壓重塊的功能，減小邊主跨比較小產(chǎn)生的主塔彎曲和主跨主梁下?lián)希?/p>

2) 輔助墩的存在一定程度上限制了壓重塊的運(yùn)動，影響了TMD的減震效果，因此在輔助墩存在時，壓重塊型TMD對地震動響應(yīng)的減震控制效果并不明顯；

3) 在無輔助墩時，壓重塊型TMD對邊跨跨中和主跨L/4都有很顯著的控制效果，其減震率分別達(dá)到了21%和15%，因此在無輔助墩的斜拉橋上采用TMD時能夠取得更好的控制效果。

[1] 張喜剛, 劉 高, 馬軍海. 中國橋梁技術(shù)的現(xiàn)狀與展望[J]. 科學(xué)通報, 2016，(Z1):415—425.

Zhang Xigang, Liu Gao, Ma Junhai. Status and prospect of technical development for bridges in China[J]. Chinese Science Bulletin, 2016，(Z1):415—425.

[2] Siringoringo D M, Fujino Y, Namikawa K. Seismic response analyses of the Yokohama Bay cable-stayed bridge in the 2011 great East Japan earthquake[J]. Journal of Bridge Engineering, 2013, 19(8): A4014006.

[3] 李春祥, 劉艷霞, 王肇民. 質(zhì)量阻尼器的發(fā)展[J]. 力學(xué)進(jìn)展, 2003, 33(2):194—206.

Li Chunxiang, Liu Yanxia, Wang Zhaomin. A review on mass dampers[J]. Advances in Mechanics, 2003, 33(2):194—206.

[4] 謝紹松, 張敬昌, 鐘俊宏. 臺北101大樓的耐震及抗風(fēng)設(shè)計(jì)[J]. 建筑施工, 2005, 27(10):7—9.

Xie Shaosong, Zhang Jingchang, Zhong Junhong. Aseismatic and wind-resisting design for Taipei 101[J]. Building Construction, 2005, 27(10):7—9.

[5] Chen Y, Cao T, Ma L, et al. Structural vibration passive control and economic analysis of a high-rise building in Beijing[J]. Earthquake Engineering & Engineering Vibration, 2009, 8(4):561—568.

[6] 顧金鈞, 趙煌澄, 邵克華. 九江長江大橋應(yīng)用新型TMD抑制吊桿渦激[J]. 土木工程學(xué)報, 1994, 27(3):3—13.

Gu Jinjun, Zhao Huangcheng, Shao Kehua. Application of new TMD to suppressing vortex-shedding vibration of hangers of Jiujiang bridge over Yangtze River[J]. China Civil Engineering Journal, 1994, 27(3):3—13.

[7] 徐 剛, 王靖夫, 任文敏,等. 施工中大橋橋塔的TMD減振研究[J]. 工程力學(xué), 2003, 20(6):106—110.

Xu Gang, Wang Jingfu, Ren Wenmin, et al. Reduction of vibration during construction of bridge towers by TMD[J]. Engineering Mechanics, 2003, 20(6):106—110.

[8] 樊健生, 陳 宇, 聶建國. 人行橋的TMD減振優(yōu)化設(shè)計(jì)研究[J]. 工程力學(xué), 2012, 29(9):133—140.

Fan Jiansheng, Chen Yu, Nie Jianguo. Optimum design of tuned mass damper for footbridge[J]. Engineering Mechanics, 2012, 29(9):133—140.

[9] 張 晶, 王志強(qiáng), 范 進(jìn), 等. 調(diào)諧質(zhì)量阻尼器(TMD)在大跨斜拉橋減震控制中的應(yīng)用[J]. 工業(yè)建筑, 2007, 37(Z1):292—294.

Zhang Jing, Wang Zhiqiang, Fan Jin. Application of tuned mass damper for controlling vibration of a stayed-cable bridge under earthquake excitation[J]. Industrial Construction, 2007, 37(Z1):292—294.

[10] Xing Chenxi, Wang Hao, Li Aiqun, et al. Study on wind-induced vibration control of a long-span cable-stayed bridge using TMD-type counterweight[J]. Journal of Bridge Engineering, 2014, 19(1):141—148.

[11] Wang Hao, Hu Ruomei, Xie Jing, et al. Comparative study on buffeting performance of Sutong Bridge based on design and measured spectrum[J]. Journal of Bridge Engineering, 2013, 18(7):587—600.

[12] Ernst H J. Der e-modul von seilen unter berücksichtigung des durchhanges[J]. Der Bauingenieur, 1965, 40(2):52—55.

[13] American ANSYS Corporation. ANSYS Advanced Analysis Techniques Guide, Release 9.0[M]. Canonsburg: ANSYS Inc., 2005.

[14] 范立礎(chǔ), 胡世德, 葉愛君. 大跨度橋梁抗震設(shè)計(jì)[M]. 北京:人民交通出版社, 2001.

[15] 公路橋梁抗震設(shè)計(jì)細(xì)則(JTG/T B02-01—2008)[S]. 北京：人民交通出版社, 2008.

Guidelines for seismic design of highway bridges (JTG/T B02-01—2008)[S]. Beijing:China Communications Press, 2008.