含裂紋復合兩級行星輪系振動特性研究

李國彥， 李方義， 劉浩華， 董德浩， 張珊珊

(1.太原理工大學新型傳感器與智能控制教育部與山西省重點實驗室， 山西 太原 030024；2.山東大學機械工程學院, 高效潔凈機械制造教育部重點實驗室， 山東 濟南 250061；3.上海航天設備制造總廠， 上海 201100)

引 言

行星式變速箱是風機、直升機、工程機械、車輛等大型復雜機械裝備傳動系統的關鍵部件。行星輪系動力學分析可從原理上揭示故障產生及演化對系統響應的影響，為其故障診斷提供理論依據。隨著數值分析理論的發展，行星輪系動力學模型由純扭轉模型向多自由度彎扭耦合模型發展。之后，許多學者對雙排行星輪系、多級行星輪系、斜齒輪、非漸開線齒輪等復雜齒輪模型進行了研究，同時模型計入時變嚙合剛度、齒側間隙、傳動誤差、摩擦、支撐剛度、阻尼等影響因素，模型由線性時不變逐漸向非線性時變模型發展。

復合行星輪系指包含一個或多個雙排行星輪系、階梯式行星輪系、多級行星輪系的齒輪傳動系統[1-5]。復合行星輪系廣泛應用于工程中，可提供更大的速比范圍，但其動力學建模具有復雜性，國內外對其動力學的研究尚處于起步階段。Kahraman[1]首次建立了雙排行星輪系純扭轉動力學模型，并對其固有特性進行了分析；Kiracof[2]將雙排行星輪系、階梯式行星輪系和多級行星輪系統一描述為復合行星輪系，研究其模型通用表達式，并對其固有特性的物理意義進行了闡述；Guo等[3-5]對復合行星輪系的嚙合相位關系及固有特性進行了分析；宋軼民等[6]建立了3K-Ⅱ型直齒行星輪系的平移-扭轉耦合動力學模型，對其固有特性進行了分析；楊富春等[7]建立了Ravigneaux型復合行星輪系平移-扭轉耦合動力學模型，并計入傳遞誤差對系統固有特性的影響；劉振皓和巫世晶等[8-9]建立了Ravigneaux型復合行星輪系純扭轉動力學模型，基于諧波平衡法得到系統基頻穩態響應，并研究了時變嚙合剛度、負載、齒側間隙等參數對系統頻響特性的影響；羅玉濤等[10]建立了混合動力兩級行星輪系純扭轉動力學模型，并研究了耦合剛度對系統固有特性的影響。

已有模型只針對健康復合行星輪系進行分析，沒有引入損傷激勵。并且，文獻[3-9]中涉及到時變嚙合剛度研究中，通常根據國家標準或石川法計算平均嚙合剛度，基于嚙合頻率將輪齒綜合嚙合剛度簡化為矩形或梯形波周期函數，再將其展開為傅立葉級數的有限次諧波項進行表達，不能準確反映復合行星輪系的傳動模式。文獻[11-12]中考慮損傷激勵時，通過引入損傷程度系數(常數值)來衡量輪齒剛度變化，不能準確描述損傷幾何參數與嚙合剛度值之間的量化關系。并且，行星輪系中包含多個嚙合副，各嚙合副之間存在嚙合相位差，目前很少有研究準確地描述復合多級行星輪系各嚙合副間的嚙合相位關系。因此，現有的模型獲取的振動響應的準確性不足，無法有效地指導其故障診斷，需建立故障復合行星輪系動力學模型、修正模型參數，深入研究故障程度和模型參數之間的相互關系，在此基礎上揭示復合行星輪系故障特性。

本文以工程機械復合兩級行星輪系為研究對象，建立平移-扭轉耦合動力學模型。對時變嚙合剛度及其嚙合相位進行分析。推導裂紋輪齒時變嚙合剛度計算公式，研究裂紋演化對系統時變嚙合剛度的影響。求解系統運動微分方程，研究系統在正常及裂紋故障情況下的固有特性。綜合運用時間歷程、階次譜、相軌跡及Poincaré映射圖，分析裂紋擴展對系統非線性振動響應的影響。為復合行星輪系動態特性分析及故障診斷提供依據。

1 復合行星輪系結構分析

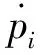
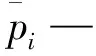
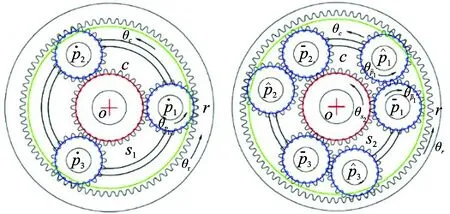
圖1 復合行星輪系結構簡圖Fig.1 Compound planetary gear set

2 復合行星輪系平移-扭轉耦合動力學模型

2.1 模型描述

為方便建模，適當簡化模型并做如下假設：(1) 建立系統集中參數動力學模型；(2) 各齒輪為漸開線標準直齒輪，齒輪間的嚙合簡化為彈簧-阻尼結構，剛度系數為嚙合齒輪副的時變嚙合剛度，阻尼系數與嚙合剛度呈線性關系；(3) 軸和軸承的支撐簡化為彈簧-阻尼結構，剛度系數為支撐剛度，阻尼系數設為常數；(4) 不考慮系統的摩擦和誤差；(5) 各構件具有三個自由度，沿與軸線垂直的兩個正交方向的平移自由度和繞自身軸線的扭轉自由度；(6) 模型采用絕對坐標系。由此可得復合兩級行星輪系平移-扭轉耦合動力學模型，如圖2所示。

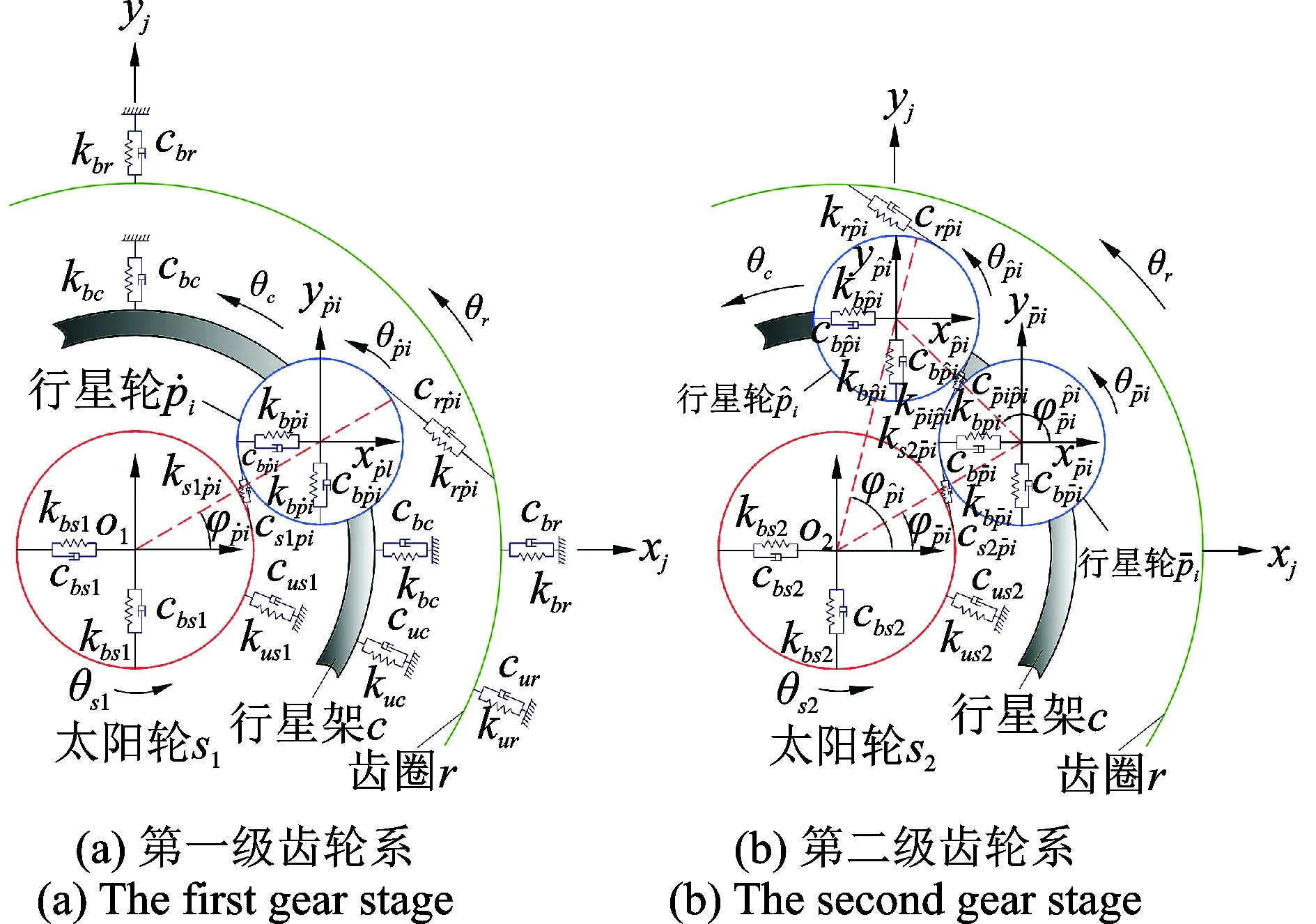
圖2 復合行星輪系動力學模型Fig.2 Dynamic model of the compound planetary gear set

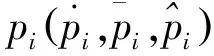
2.2 構件間相對位移分析

假設旋轉方向以逆時針方向為正方向，沿嚙合線方向以壓縮為正方向。各嚙合副的相對位移δg如下：

(1)

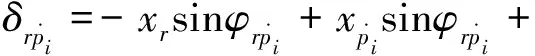
(2)

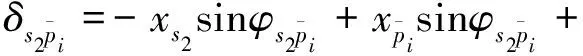
(3)

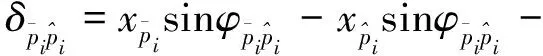
(4)

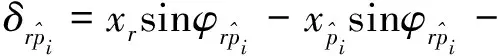
(5)

行星架相對于行星輪的線位移的表達式為：

δcpix=xc-xpi-sinφpiuc

(6)

δcpiy=yc-ypi+cosφpiuc

(7)

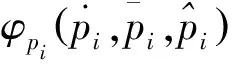
(8)

2.3 運動微分方程

采用牛頓第二定律建立運動微分方程[13]：

(9)

(10)

(11)

(12)

(13)

(14)

(15)

式中mj和Ij分別代表各構件的質量和質量慣性矩；x和y代表平移振動；Tin和Tout分別代表輸入和輸出轉矩；Fg代表各嚙合副嚙合力；Fbjx,Fbjy和Fuj分別代表各中心構件在各振動方向上的支撐力；Fcpix和Fcpiy代表各行星輪支撐力。

各嚙合副的嚙合力為

(16)

中心構件在各振動方向上的支撐力為

(17)

行星架對行星輪的支撐力為

(18)

整理式(1～18)可得到系統運動矩陣方程

Km+KbQt=T

(19)

式中M為質量矩陣，Q為位移矩陣，Cm為嚙合阻尼矩陣，Cb為支撐阻尼矩陣，Km為嚙合剛度矩陣，Kb為支撐剛度矩陣，T為外加負載矩陣。

該復合行星輪系的基本參數如表 1所示。

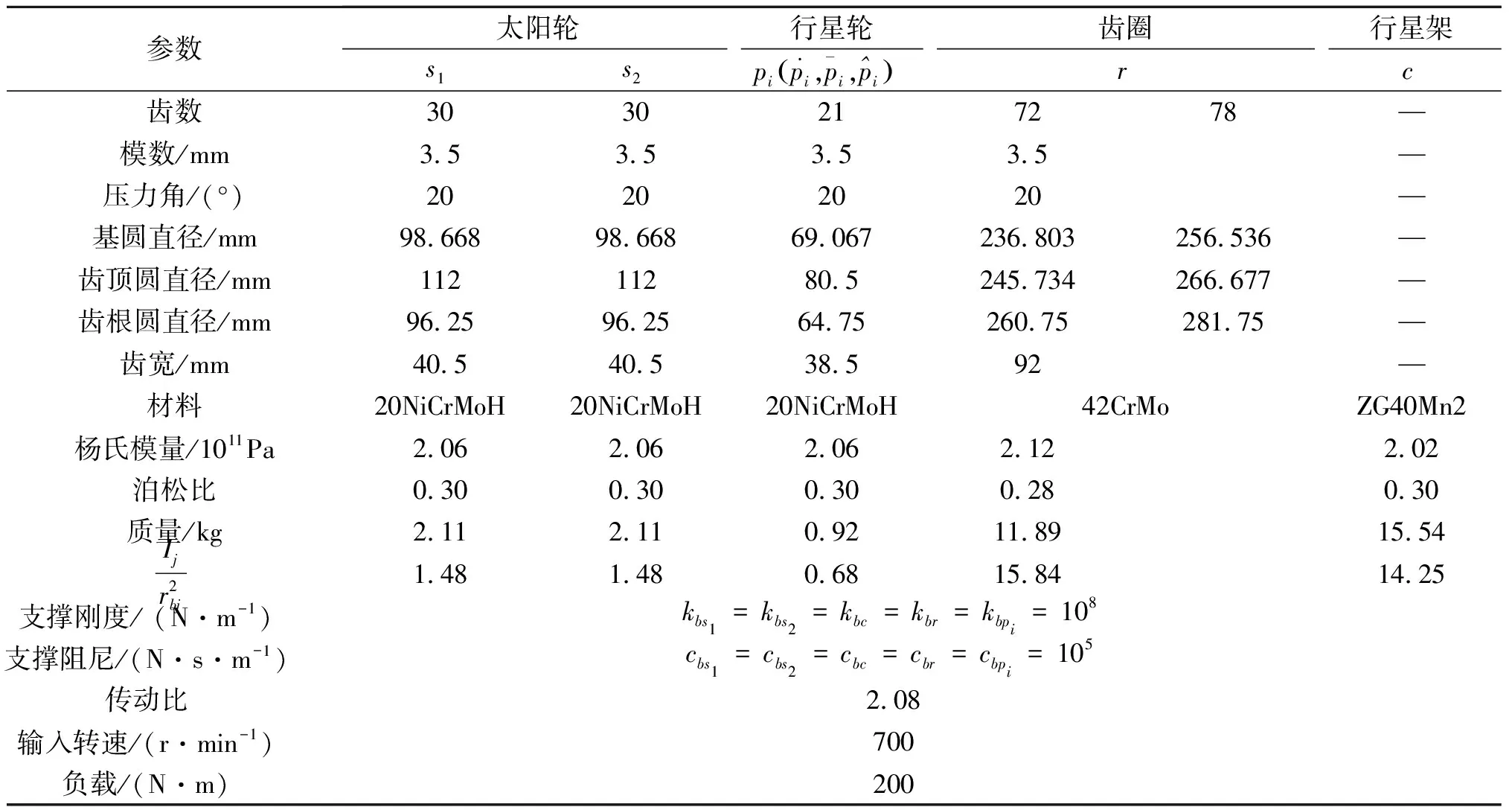
表1 復合行星輪系的基本參數

3 時變嚙合剛度

剛度激勵是齒輪傳動中最主要的內部激勵形式之一。在不考慮重合度的情況下，每個輪齒可看作變截面的懸臂梁，在齒面載荷的作用下發生變形。一般認為，輪齒的變形主要由切向力和附加彎矩引起的彎曲變形、切向力引起的剪切變形、徑向力引起的壓縮變形及齒面接觸力引起的接觸變形等組成。

本文將輪齒簡化為齒根圓上的懸臂梁，分別計算輪齒各嚙合剛度分量、單齒綜合嚙合剛度及多齒綜合嚙合剛度。針對齒輪裂紋損傷，推導裂紋輪齒時變嚙合剛度計算公式，研究裂紋擴展對時變嚙合剛度的影響。

3.1 正常輪齒時變嚙合剛度分析

單齒懸臂梁模型如圖 3所示。圖中，懸臂梁的有效長度為da，即從齒頂圓到齒根圓的長度。由于齒根過渡圓弧很難用確定的方程表示，本文將其簡化為直線段d1。Fn是沿嚙合線方向的法向嚙合力；Fa和Fb分別為沿正交方向的兩個嚙合分量，可以表示為：Fa=Fnsinα1，Fb=Fncosα1；α1代表各嚙合點對應的嚙合角；d代表嚙合點到齒根處的水平距離；h代表嚙合點到輪齒中心線的豎直距離；rb和rf分別為輪齒基圓半徑和齒根圓半徑；α2為齒輪基圓圓弧對應的圓心半角；α3為齒輪近似齒根圓弧對應的圓心半角。

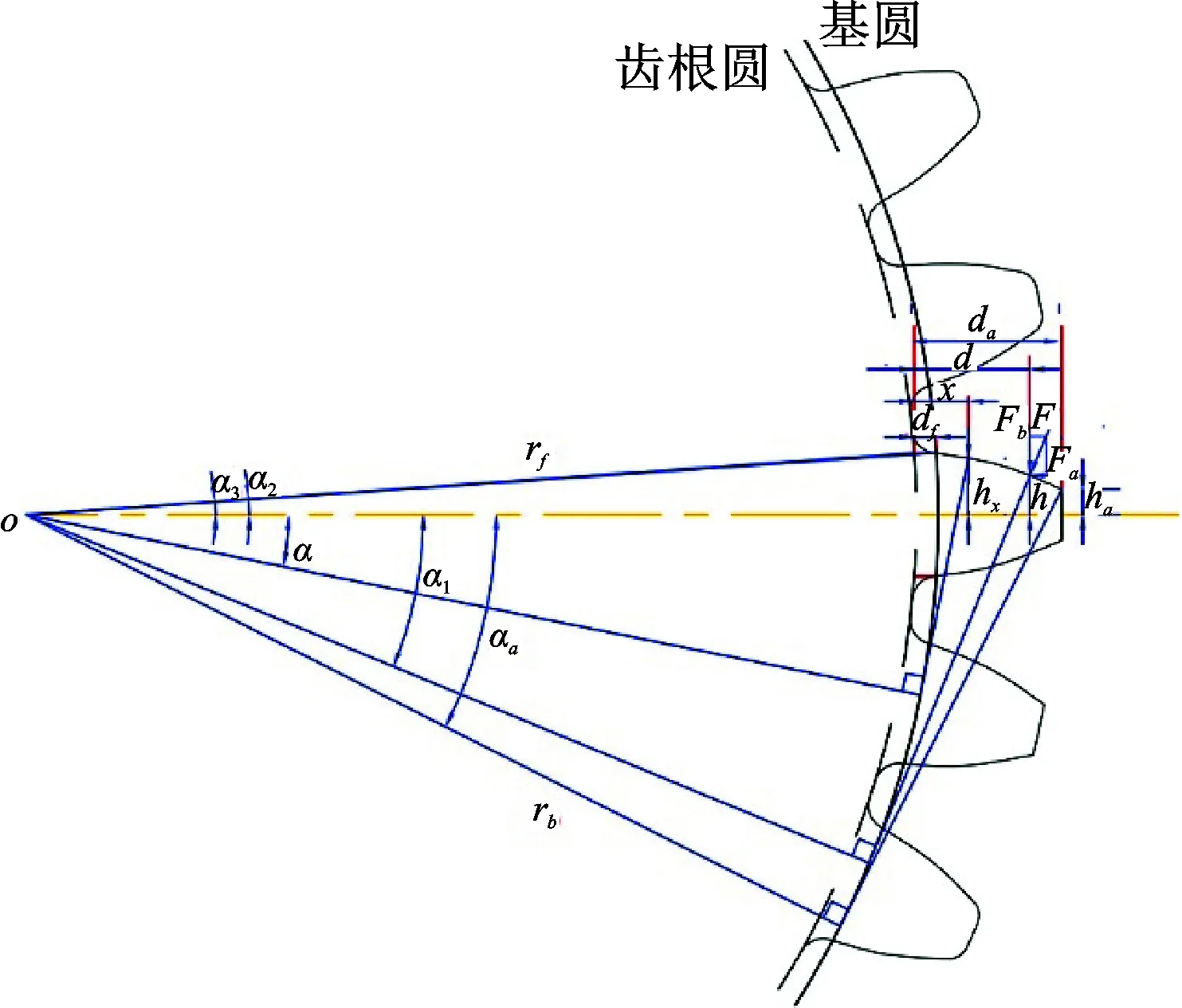
圖3 正常輪齒懸臂梁模型Fig.3 Cantilever beam model for a perfect tooth

根據梁理論，輪齒彎曲剛度kb、剪切剛度ks和軸向壓縮剛度ka的微分方程為[14-16]：

(20)

(21)

(22)

根據赫茲接觸理論，赫茲接觸剛度kh表示為[14-16]

(23)

式中E和G為楊氏模量和剪切模量，υ為泊松比。

圖 4展示了正常輪齒模型及其橫截面sx。如圖所示，橫截面sx的形狀為矩形，用A-B-C-D表示，其面積Ax和慣性矩Ix表示為：

Ax=2hxB=

(24)

(25)

式中hx為橫截面sx寬度的一半，B為齒寬。

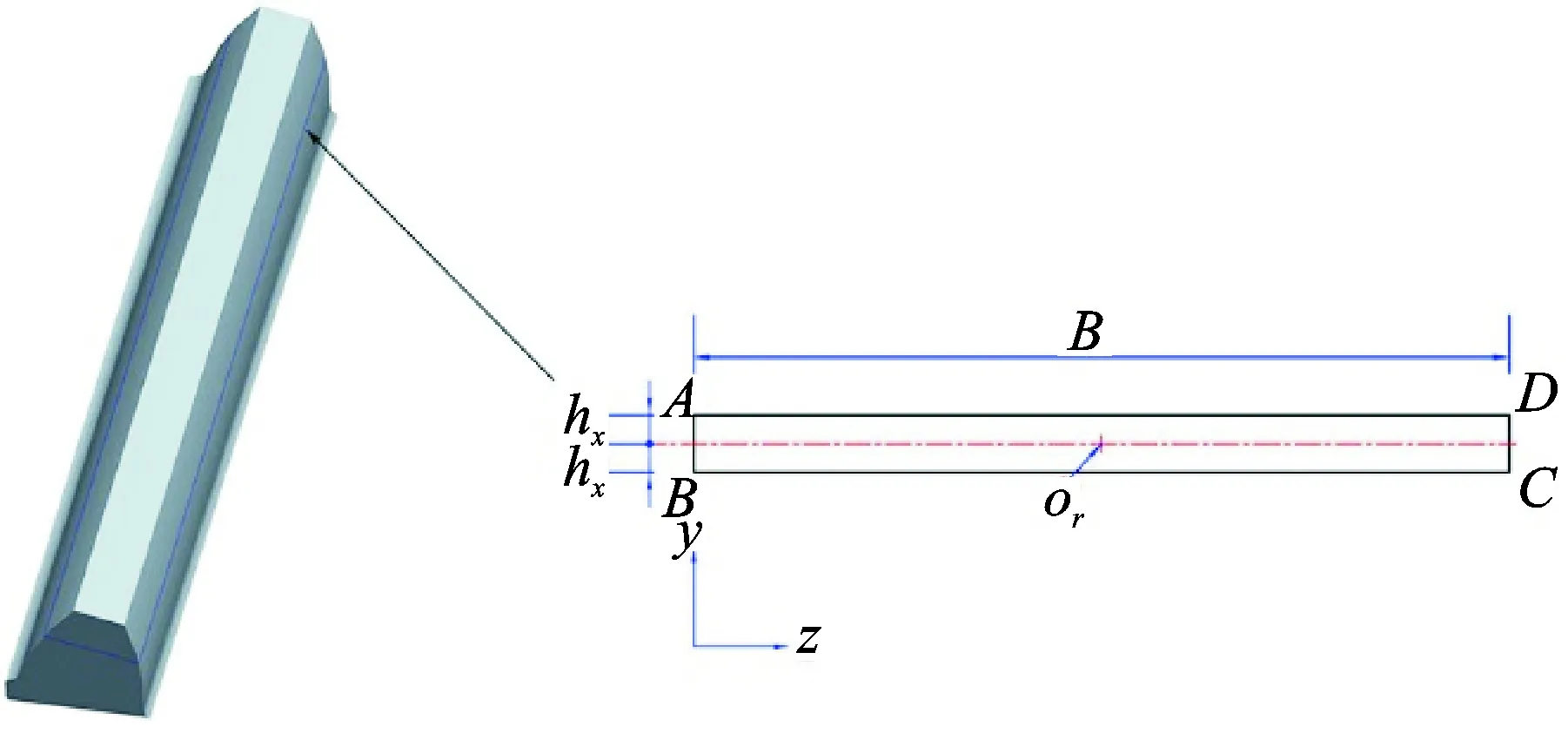
圖4 正常輪齒模型及其橫截面Fig.4 Perfect tooth model and the cross-section

由于重合度的影響，一個嚙合周期內存在單齒和雙齒嚙合區。單齒綜合嚙合剛度表示為：

(26)

多齒綜合嚙合剛度表示為

kg=

(27)

其中，下標1代表一對齒輪副中的主動輪，下標2代表從動輪。i=1代表雙齒嚙合區的第一對嚙合副，i=2代表第二對嚙合副。

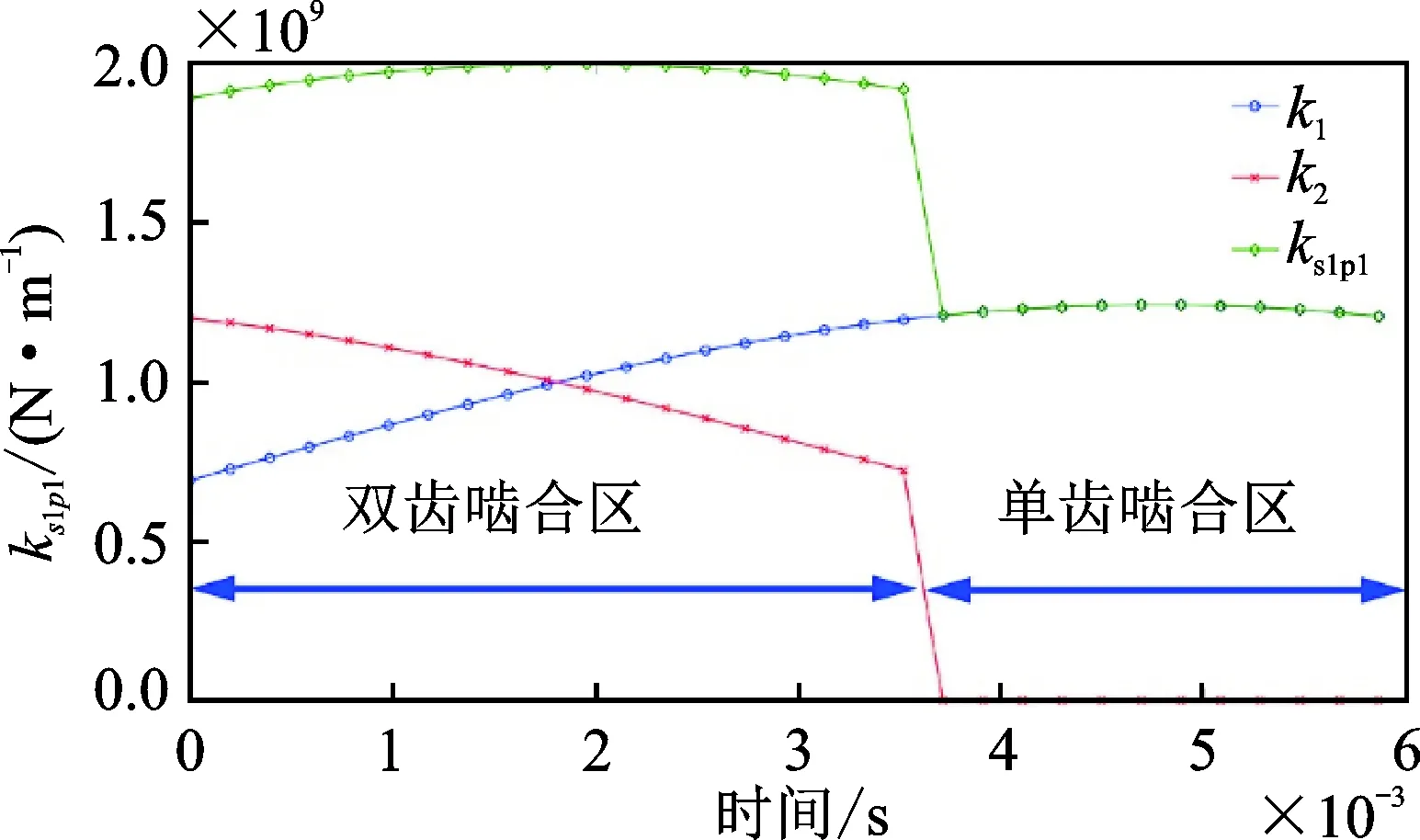
圖5 第一級太陽輪-行星輪嚙合副時變嚙合剛度曲線Fig.5 Time-varying mesh stiffness curve of the gear mesh in the first gear stage

3.2 裂紋輪齒時變嚙合剛度分析

根據文獻[14-15]，假設裂紋產生于太陽輪齒根處，沿與輪齒中心線呈v=45°的方向擴展，裂紋尺寸用q1表示，當裂紋擴展到與輪齒中心線相交時，定義裂紋程度為50%。之后裂紋改變擴展方向，沿與輪齒中心線呈v=-45°的方向擴展，裂紋尺寸用q2表示，直到與齒根圓相交，定義裂紋程度為100%(對應的裂紋總長度為9.42 mm)。圖 6為裂紋輪齒模型及橫截面。

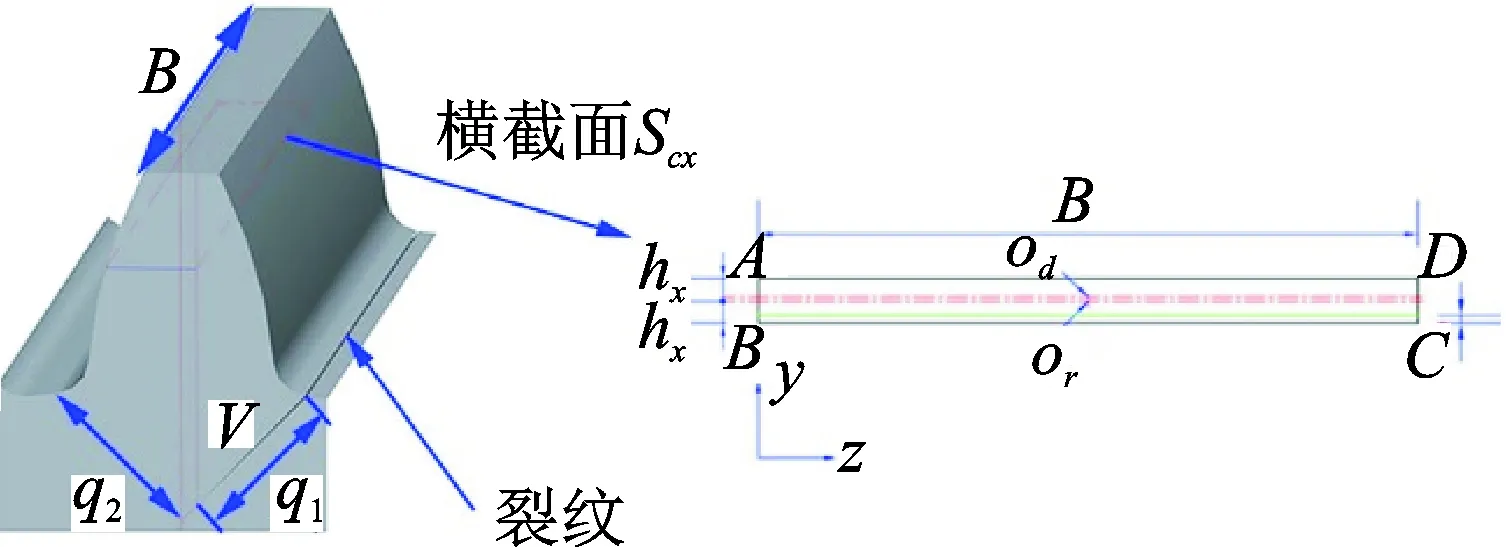
圖6 裂紋輪齒模型及其橫截面Fig.6 Cracked tooth model and the cross-section

裂紋不影響赫茲接觸剛度與軸向壓縮剛度，當輪齒進入損傷區域嚙合時，輪齒的橫截面相對于正常情況發生改變，導致彎曲剛度和剪切剛度的計算公式發生改變。

當裂紋未擴展至輪齒中線時，輪齒橫截面的面積和慣性矩為(圖 7(a))：

Ax=hx+hdB=

(28)

(29)

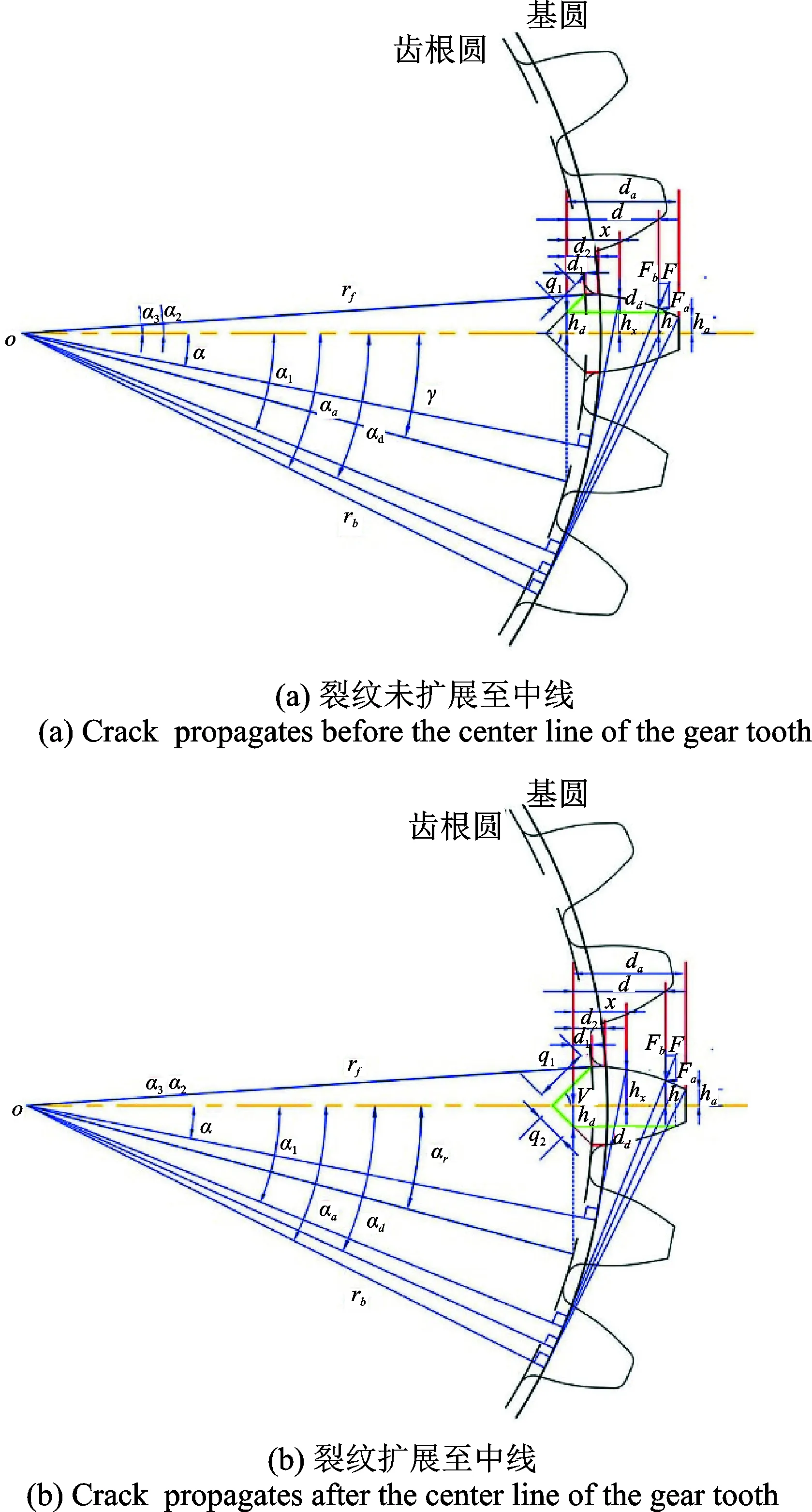
圖7 裂紋輪齒懸臂梁模型Fig.7 Cantilever beam model for a cracked tooth

當裂紋擴展至輪齒中線后，輪齒橫截面的面積和慣性矩為(圖 7(b))：

Ax=hx-hdB=

(30)

(31)

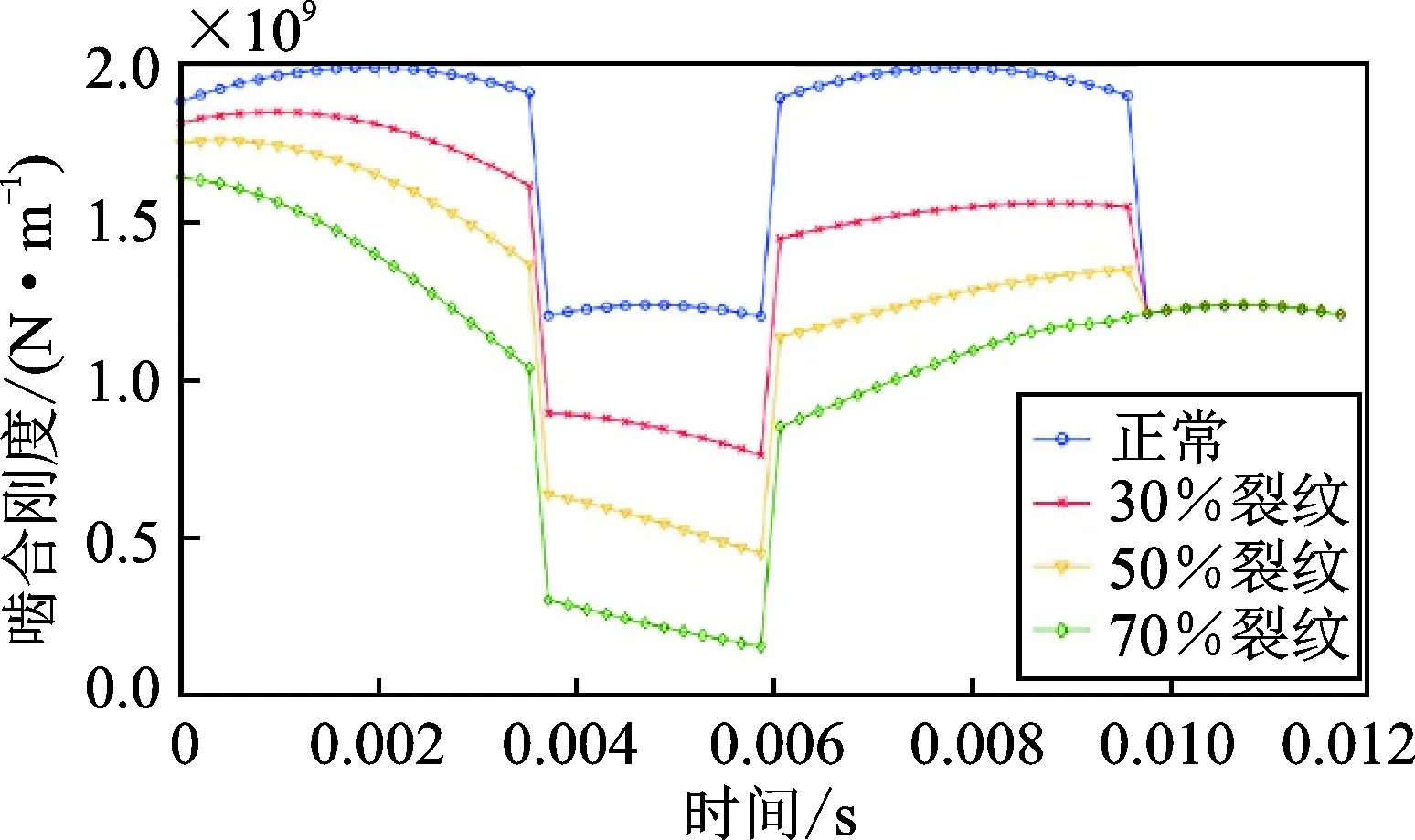
圖8 裂紋對第一級太陽輪-行星輪嚙合副時變嚙合剛度的影響Fig.8 Effects of the crack propagation on the time-varying mesh stiffness of the mesh pair in the first gear stage

3.3 嚙合相位分析

本文所研究的復合行星輪系包含兩級齒輪系。整個系統中任意兩個不同的嚙合副，輪齒的接觸均可能存在時間差。因此，要分析的嚙合相位關系分為：⑴ 同一種嚙合副之間的嚙合相位關系；⑵ 同一級齒輪系不同種嚙合副之間的嚙合相位關系；⑶ 不同級齒輪系，各級嚙合副之間的嚙合相位關系。

同一種嚙合副之間的相位關系計算公式如表2所示。

表2 同一種嚙合副相對嚙合相位計算公式

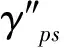
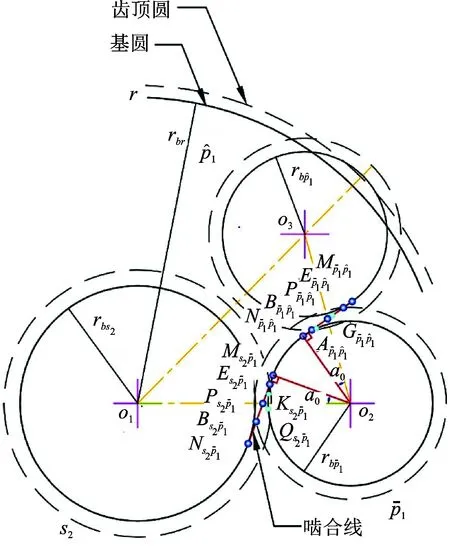
圖9 嚙合示意圖Fig.9 Mesh sketch

(32)

(33)

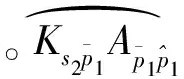
(34)

第二級第一個太陽輪-行星輪嚙合副相對于第一級第一個太陽輪-行星輪嚙合副的相位差具體數值由制造安裝時決定，本文取0。

考慮嚙合相位差，各嚙合副綜合時變嚙合剛度的表達式為

kgt=kgt-γtmn

(35)

式中tmn為第n級齒輪系的嚙合周期。圖 10為考慮嚙合相位差的時變嚙合剛度曲線。

4 復合行星輪系固有特性分析

固有特性分析包括對固有頻率和振型的求解和分析。系統自由振動微分方程為

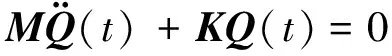
(36)

對上式進行廣義特征值問題求解

K-ω2M=0

(37)

式中K=Km+Kb，ωi為固有頻率。

通過MATLAB函數V,D=eigK,M，可得各階固有頻率及振型。

4.1 固有頻率

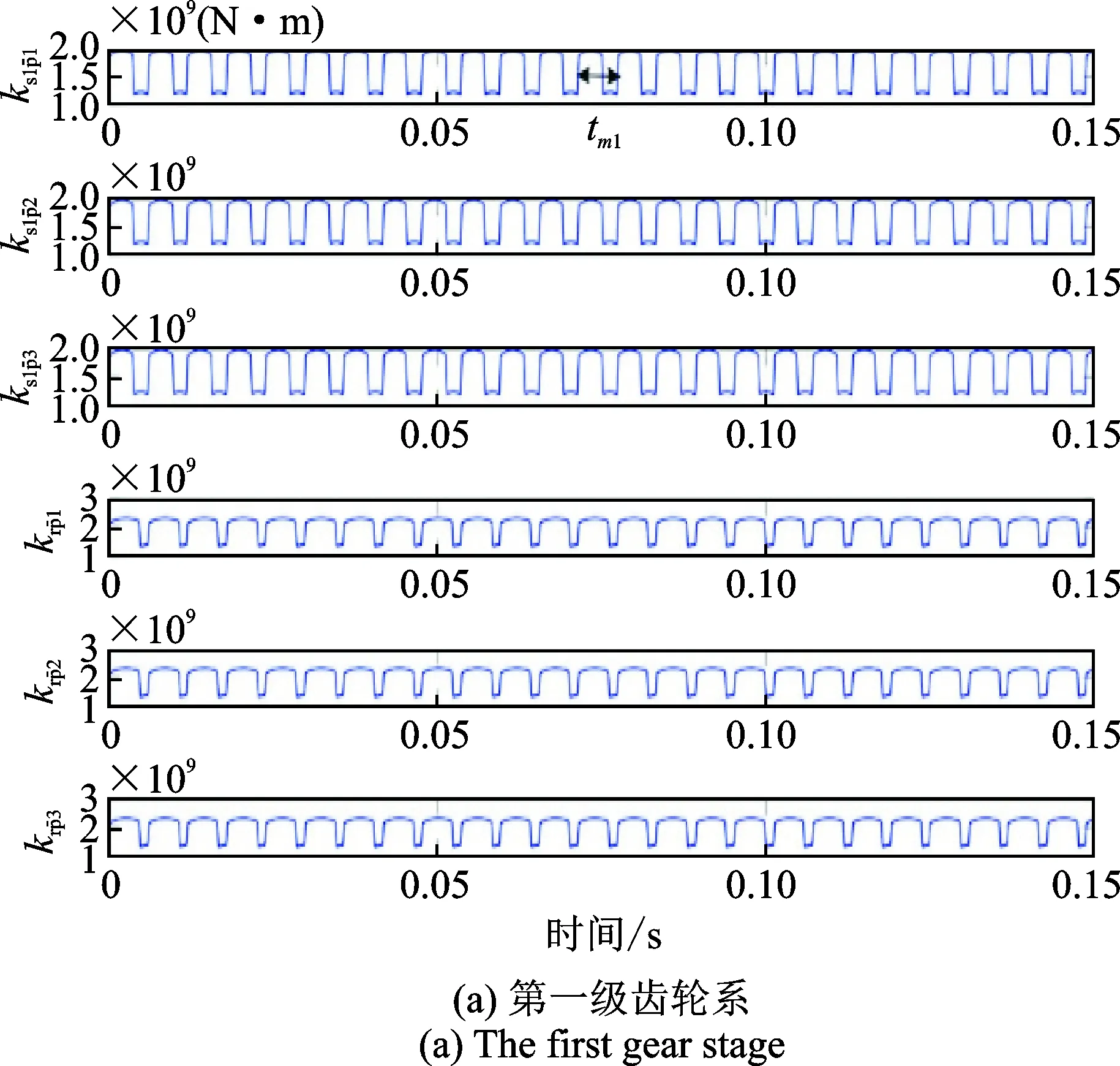
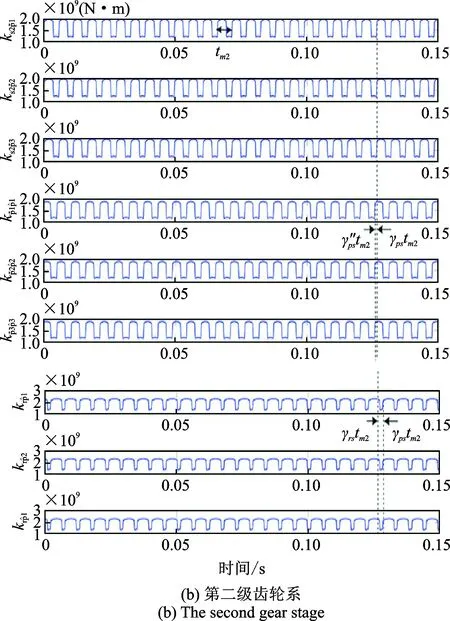
圖10 考慮嚙合相位差的時變嚙合剛度曲線Fig.10 Time-varying mesh stiffness considering the mesh phase relations

圖 11 各階固有頻率值隨時間的變化曲線Fig.11 The change curves of the natural frequencies with respect to the time

圖11展示了一個嚙合周期內固有頻率隨時間變化曲線。可以看出，由于嚙合剛度的時變性，系統固有頻率發生改變。嚙合剛度對低階固有頻率影響較小，但對高階固有頻率有明顯的影響。由于嚙合相位、嚙合周期及重合度的影響，各嚙合副在同一時間處于不同的嚙合點，因此，各階固有頻率的改變不具有單調性，并且f31和f34產生模態躍遷現象[17]。

4.2 振動模態

對于行星輪系平移-扭轉耦合動力學模型，文獻[6-7]把單級行星輪系的振動劃分為三種：中心構件平移振動模式、中心構件扭轉振動模式、行星輪振動模式(同組行星輪數量>3)。文獻[10]基于純扭轉動力學模型，把兩級行星輪系的振動劃分為整體扭轉振動模式和單排行星輪振動模式。考慮到所研究的復合兩級行星輪系平移-扭轉耦合動力學模型，根據振型矢量分析，本文將其振動劃分為：整體平移/扭轉振動模態和單級齒輪系平移/扭轉振動模態。圖 12～14展示了典型的振動模態。圖中，虛線表示各構件的初始位置，實線表示各構件振動后的位置。為清晰顯示，圖中未表示出行星架和齒圈的振動。進一步歸納可得到以下結論：

(1) 整體振動模態(圖 12)

整體平移振動模態。對應的固有頻率具有二重根。各中心構件只存在平移振動，不存在扭轉振動。兩級行星輪均以不同的幅度做振動。

整體扭轉振動模態。對應的固有頻率值為單根。各中心構件均以不同幅度做扭轉振動，不存在平移振動。兩級行星輪均在振動，同一級同一組行星輪扭轉方向具有相同的振動。

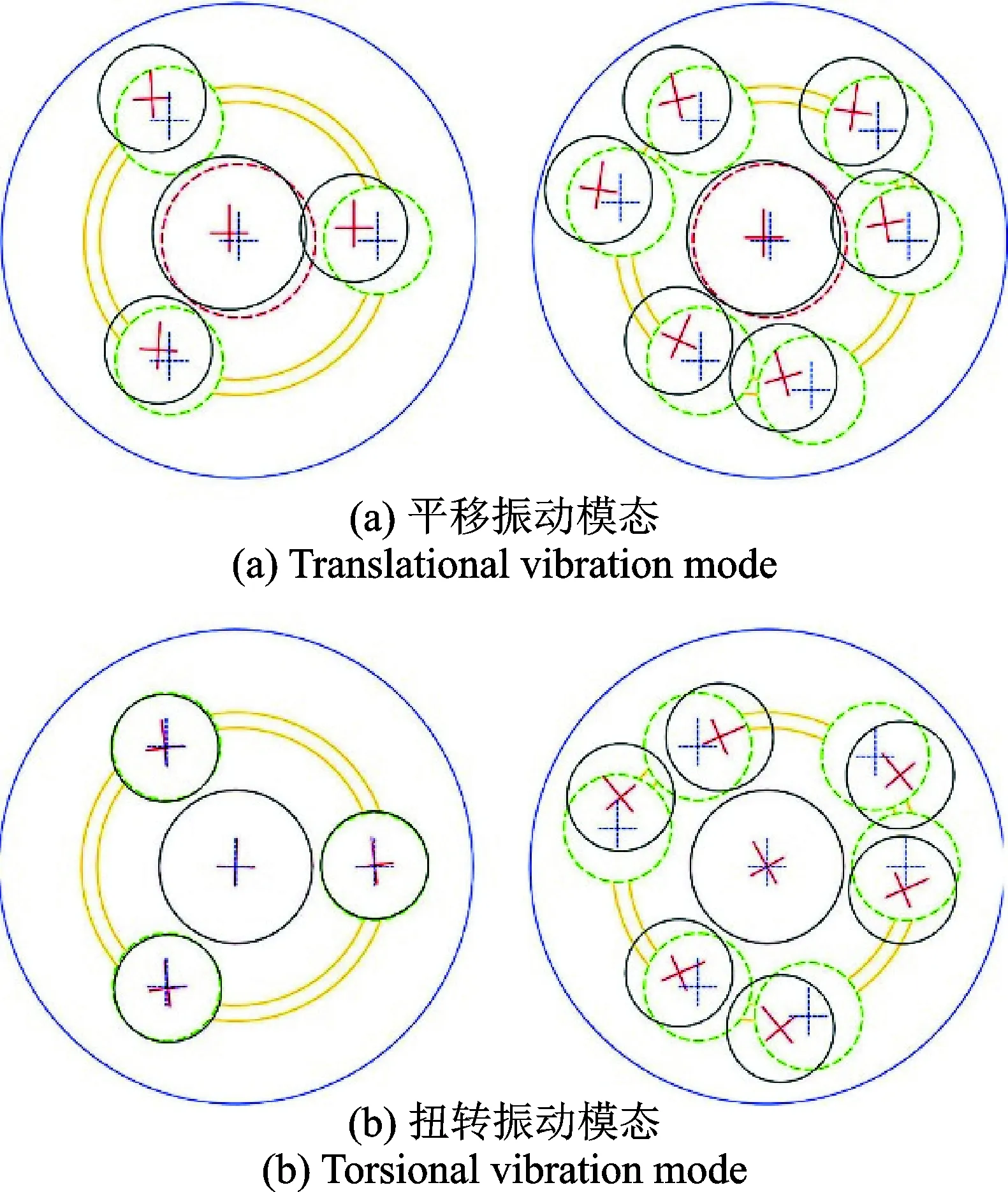
圖12 整體振動模態Fig.12 Vibration mode of all the components

(2) 第一級齒輪系振動模態(圖 13)

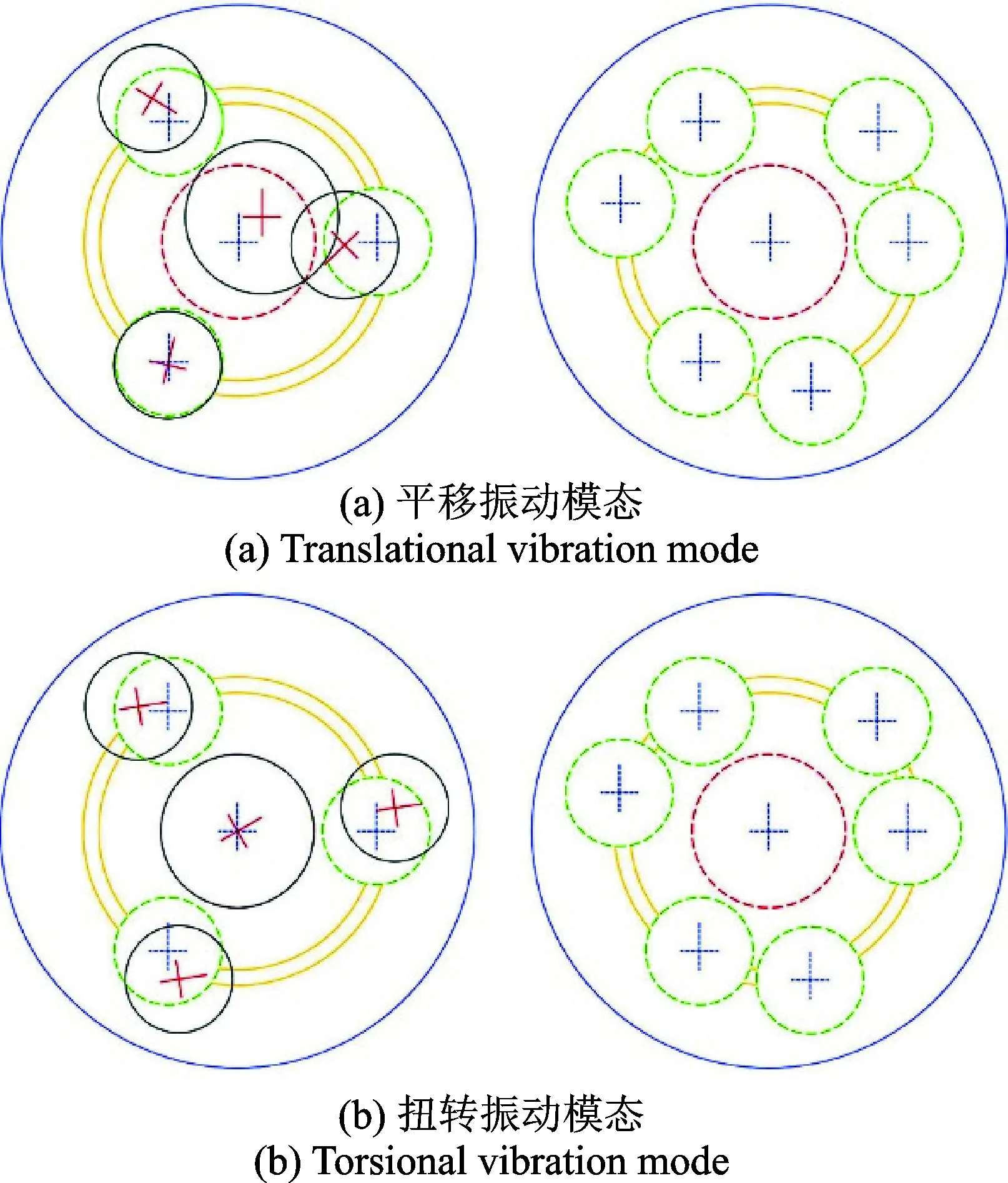
圖13 第一級齒輪系振動模態Fig.13 Vibration mode of the first gear stage

第一級齒輪系平移振動模態。對應著第34和35階固有頻率，其值為二重根。第一級中心構件只做平移振動，不存在扭轉振動。與第一級中心構件嚙合的行星輪以不同的幅度做振動。第二級構件沒有明顯的振動。

第一級齒輪系扭轉振動模態。對應著第36階固有頻率，其值為單根。第一級中心構件做扭轉振動，不存在平移振動。與第一級中心構件嚙合的行星輪振動強烈，扭轉方向具有相同的振動。第二級構件沒有明顯的振動。

(3) 第二級齒輪系振動模態(圖14)

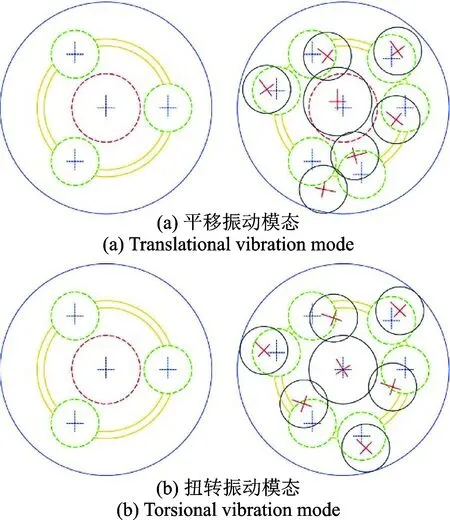
圖14 第二級齒輪系振動模態Fig.14 Vibration mode of the second gear stage

第二級齒輪系平移振動模態。對應著第37和38階固有頻率，其值為單根。第二級中心構件只做平移振動，不存在扭轉振動。與第二級中心構件嚙合的行星輪以不同的幅度做振動。第一級構件沒有明顯的振動。

第二級齒輪系扭轉振動模態。對應著第39階固有頻率，其值為單根。第二級中心構件做扭轉振動，不存在平移振動。與第二級中心構件嚙合的行星輪振動強烈，扭轉方向具有相同的振動。第一級構件沒有明顯的振動。

4.3 裂紋對固有頻率的影響

假設裂紋出現在太陽輪齒根處，沿直線從0到70%(100%裂紋程度對應的總長度為9.42 mm)間隔為10%擴展，共得到8個樣本。對比各裂紋程度下同一時間點系統各階固有頻率，可得各階固有頻率隨裂紋擴展的變化曲線，如圖 15所示。裂紋對低階固有頻率(f1～f24)影響較小，對f25，f30，f31和f37影響較大，隨裂紋擴展，這些固有頻率呈明顯的下降趨勢，系統的二重根數減少。

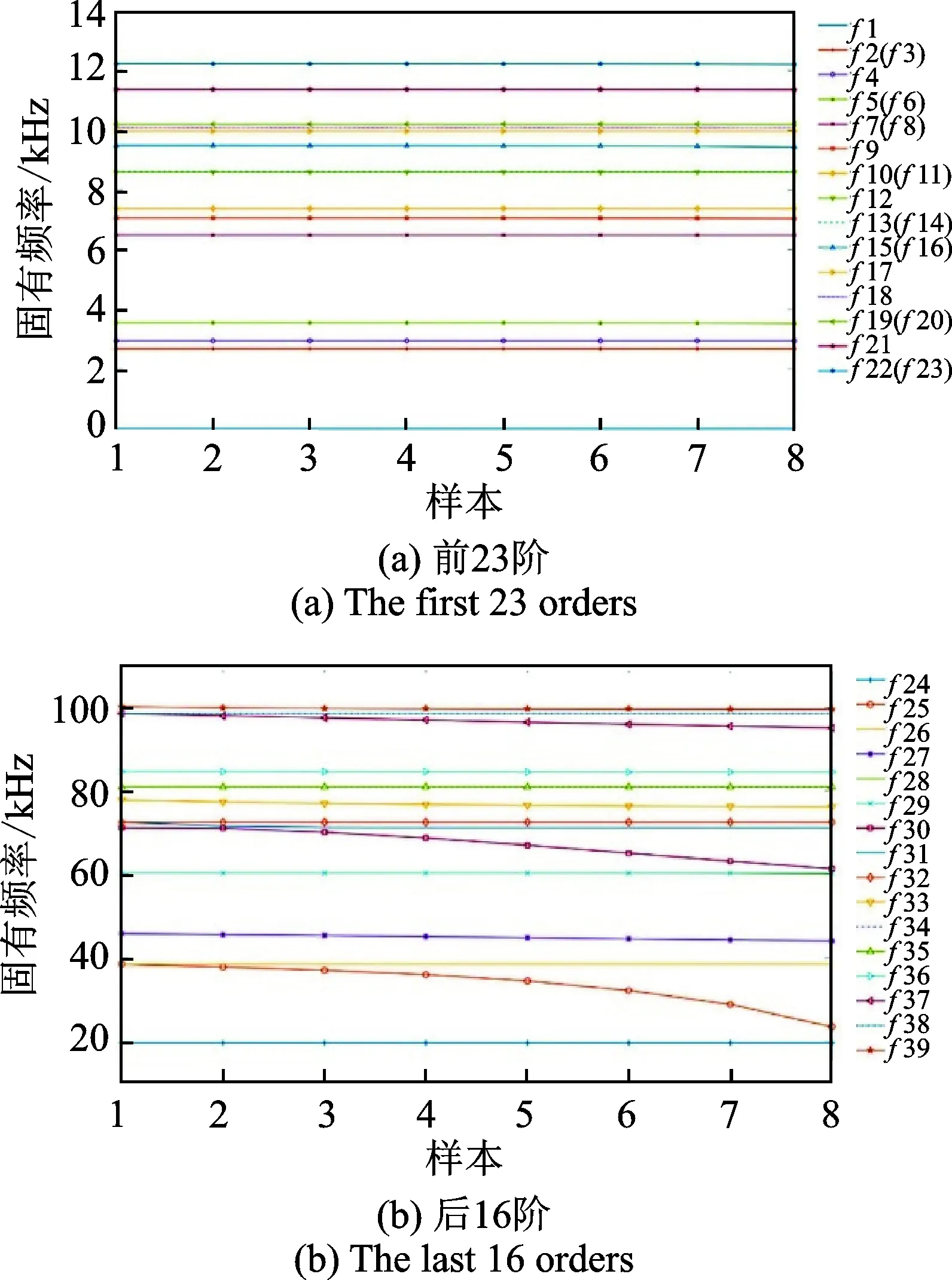
圖15 太陽輪裂紋對固有頻率的影響Fig.15 Effects of the cracked sun gear on the natural frequencies

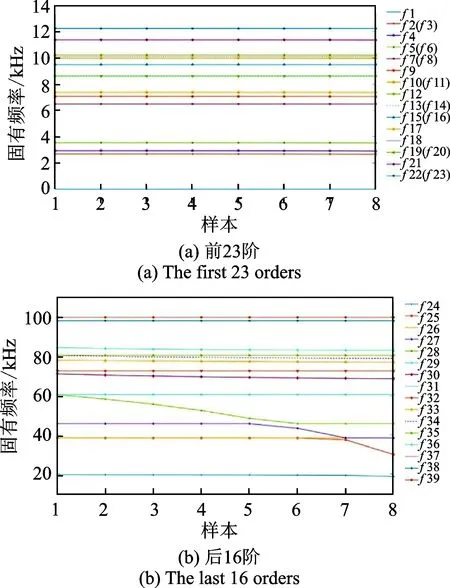
圖16 行星輪裂紋對固有頻率的影響Fig.16 Effects of the cracked planet gear on the natural frequencies

假設裂紋出現在行星輪齒根處，沿直線從0到70%(100%裂紋程度對應的總長度為8.78 mm)間隔為10%擴展，圖 16展示了行星輪裂紋對固有頻率的影響。由圖可知，低階固有頻率對裂紋不敏感，高階固有頻率f25，f27，f28和f34隨裂紋擴展明顯下降，系統的二重根數減少。

因此，可將系統固有頻率作為一個有效的故障特征。

4.4 裂紋演化對系統振動響應的影響

運用四階Runge-Kutta數值分析方法求解得到系統在不同裂紋損傷程度下的振動響應。圖17～19分別展示了太陽輪在正常、30%和50%裂紋損傷情況下的振動響應的時間歷程、階次譜、相軌跡和Poincaré映射圖。

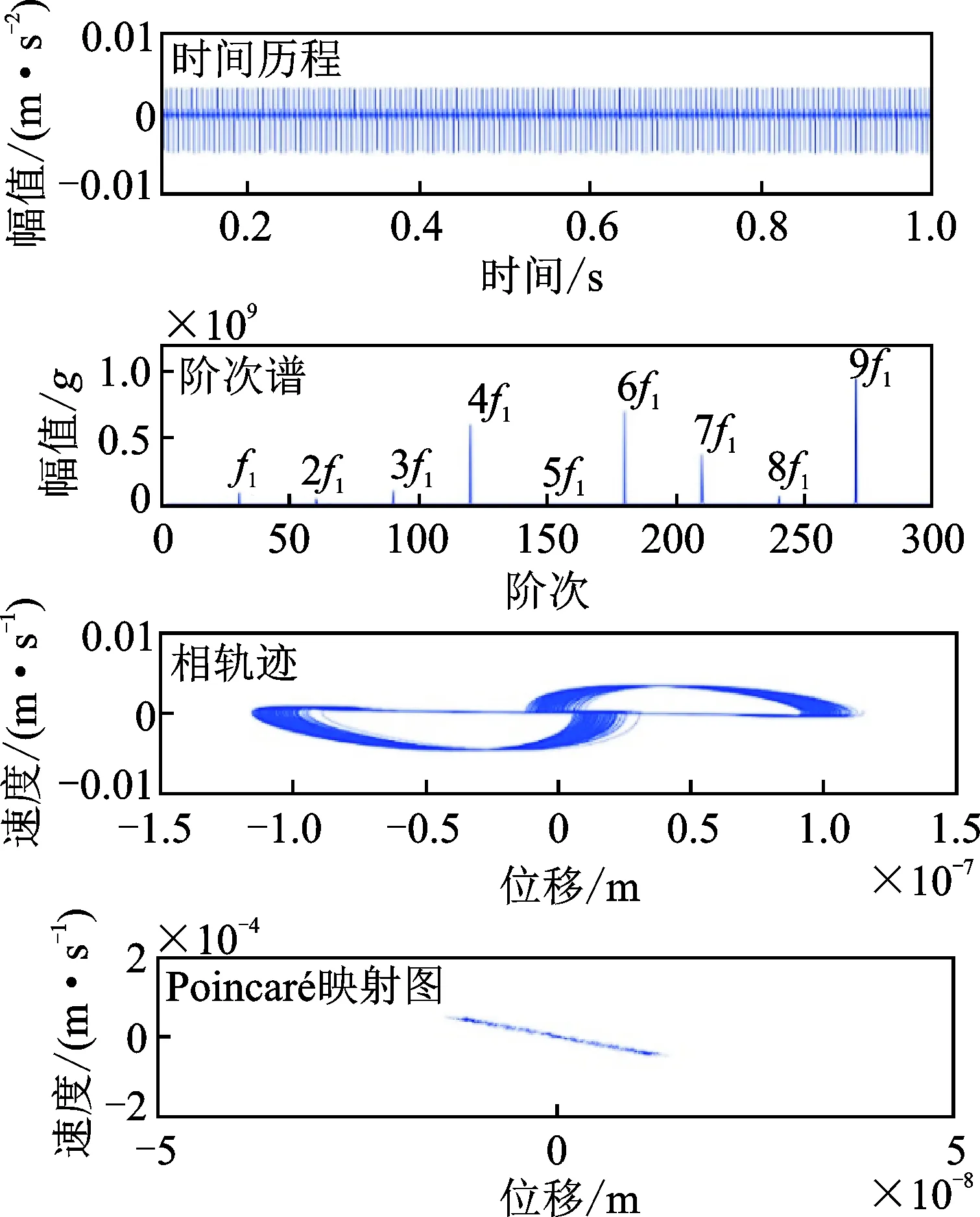
圖17 正常情況下太陽輪的振動響應Fig.17 Vibration responses of the sun gear in healthy condition

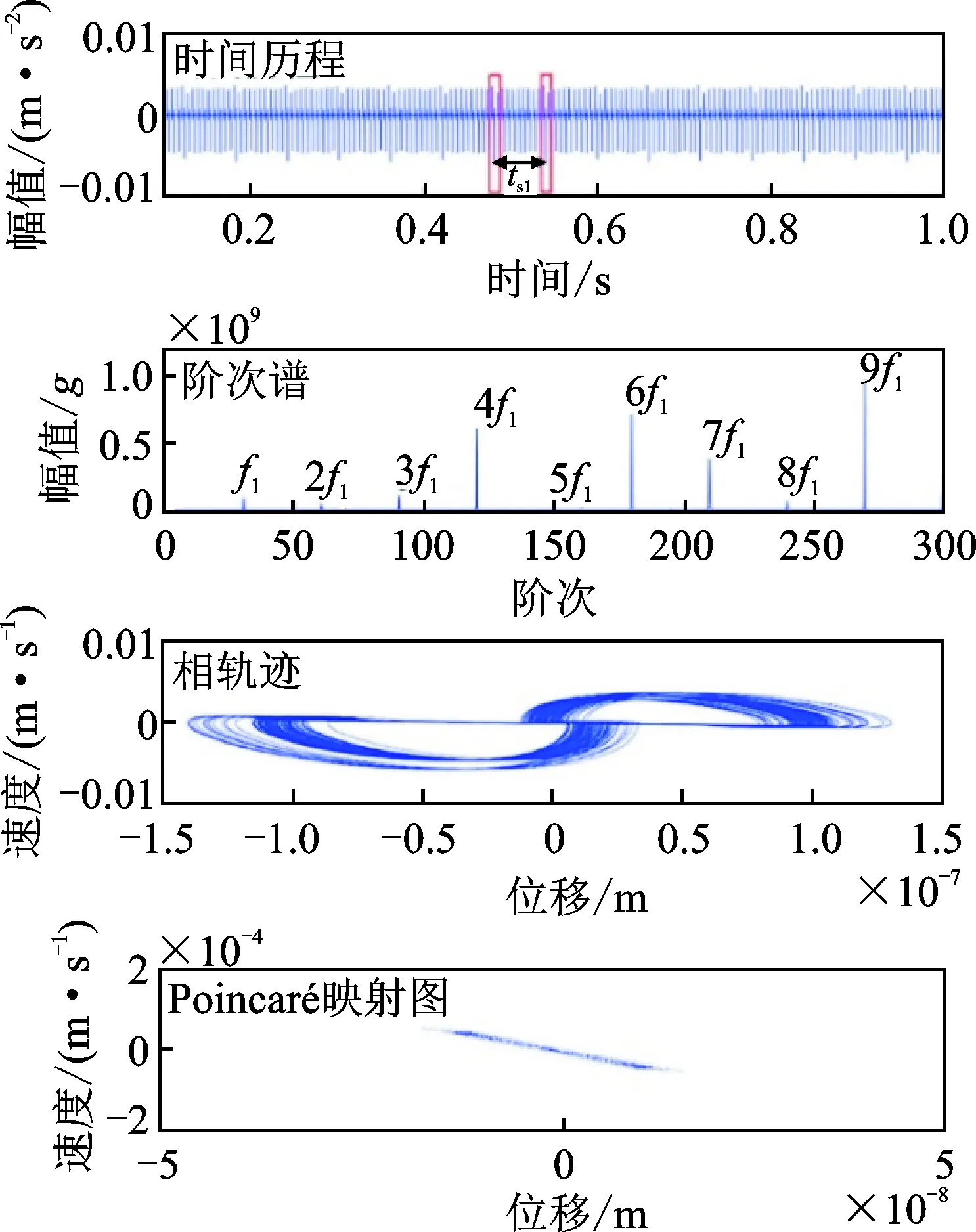
圖18 30%裂紋情況下太陽輪的振動響應Fig.18 Vibration responses of the sun gear with 30% crack

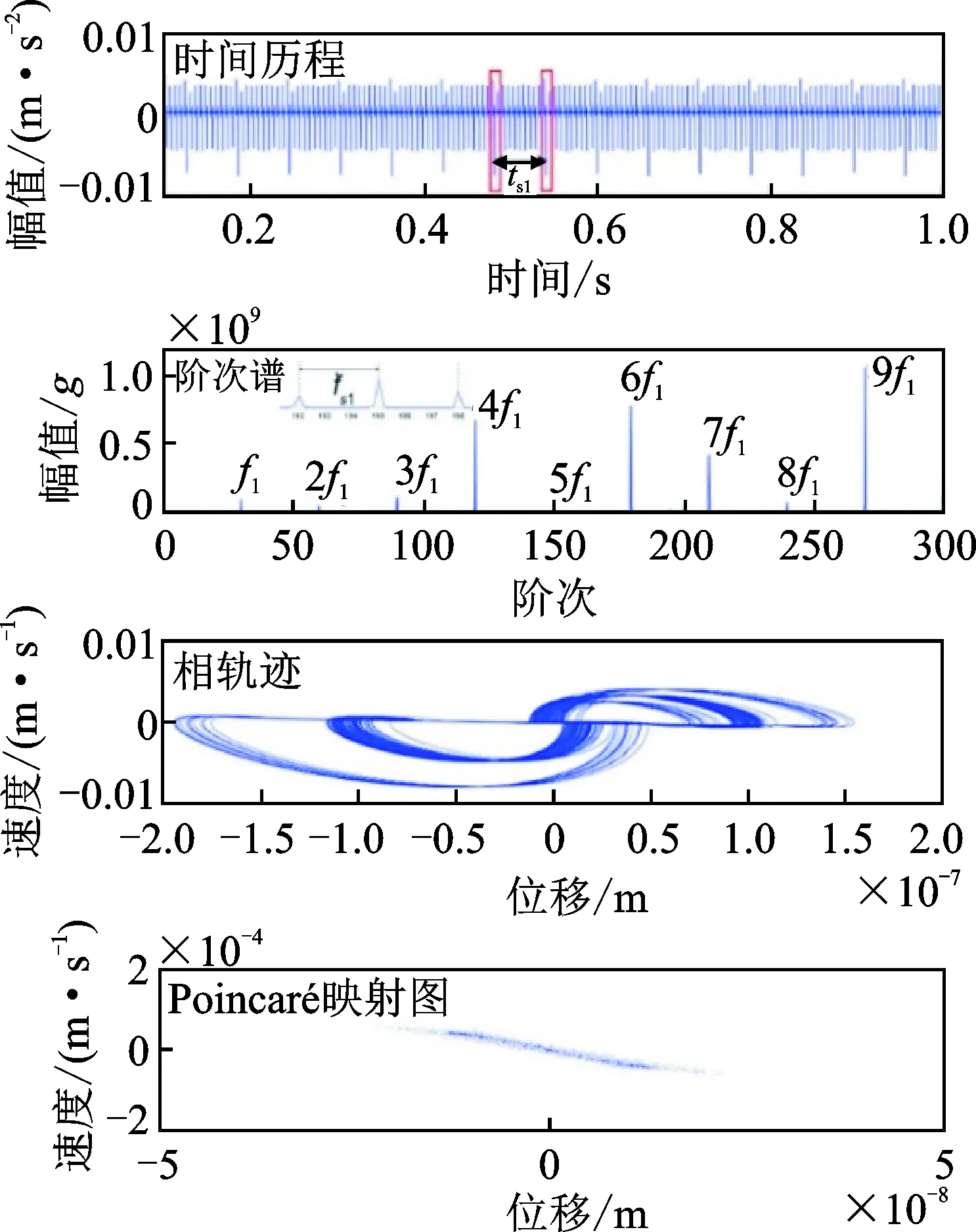
圖19 50%裂紋情況下太陽輪的振動響應Fig.19 Vibration responses of the sun gear with 50% crack

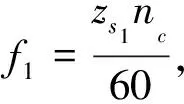
太陽輪出現裂紋時，隨著太陽輪旋轉，損傷輪齒分別與配對的三個行星輪嚙合，引起周期為0.06 s的沖擊序列。早期裂紋(30%以內)引起的沖擊序列的幅值非常微弱，隨著裂紋擴展，沖擊序列的幅值有一定的增大，但很容易被其余構件的振動響應淹沒。

對比不同裂紋程度下的振動響應的相軌跡及Poincaré映射圖可以看出，隨著裂紋的擴展，相軌跡曲線范圍顯著的向外擴展；Poincaré截面上的映射點的離散程度也明顯的增大。并且，即使在裂紋的早期階段(30%以內)，相軌跡及Poincaré映射圖的變化也非常明顯。因此，相軌跡和Poincaré映射圖可以更有效地指示早期裂紋的產生及對其演化程度進行跟蹤。

以上分析為工程中復合行星輪系故障診斷提供了理論依據。

5 結 論

(1) 以復合行星輪系為研究對象，建立了平移-扭轉耦合動力學模型，推導出系統運動矩陣微分方程；基于懸臂梁模型及嚙合原理，推導了時變嚙合剛度及其嚙合相位的計算公式；對裂紋輪齒時變嚙合剛度算法進行了推導，分析了裂紋演化對系統時變嚙合剛度的影響。該故障動力學模型可用來分析裂紋演化對系統響應的影響。

(2) 得到復合行星輪系在正常及裂紋情況下的固有特性。研究了時變嚙合剛度對固有頻率的影響，結果表明：高階固有頻率對時變嚙合剛度較為敏感，出現了模態躍遷現象。通過振型分析，將其振動模態劃分為整體平移、扭轉振動模態和單級齒輪系平移、扭轉振動模態，并歸納了各振動模態的基本特征。進一步分析了裂紋擴展對系統固有頻率的影響，研究表明：裂紋擴展對低階固有頻率影響較小，對某些高階固有頻率影響較大，隨著裂紋擴展，這些固有頻率值呈下降趨勢，系統的二重根數減少。

(3) 綜合運用時間歷程、階次譜、相軌跡、Poincaré映射圖分析了裂紋擴展對系統非線性振動響應的影響。研究表明：損傷輪齒在時域中引起了具有一定時間間隔的周期性沖擊序列，在階次譜中形成以損傷輪齒故障特征頻率為間隔的邊頻帶。隨著裂紋擴展，相軌跡曲線范圍變寬，Poincaré 映射圖離散程度增大。相軌跡和Poincaré 映射圖更有效地指示了早期裂紋的產生及對其演化程度進行跟蹤。

[1] Kahraman A. Free torsional vibration characteristics of compound planetary gear sets[J]. Mechanism and Machine Theory, 2001, 36(8): 953—971.

[2] Kiracofe D R, Parker R G. Structured vibration modes of general compound planetary gear systems[J]. Journal of Vibration and Acoustics, 2006, 129(1): 1—16.

[3] Guo Y, Parker R G. Purely rotational model and vibration modes of compound planetary gears[J]. Mechanism and Machine Theory, 2010, 45(3): 365—377.

[4] Guo Y, Parker R G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Vibration and Acoustics, 2010, 132(1): 1—13.

[5] Guo Y, Parker R G. Analytical determination of mesh phase relations in general compound planetary gears[J]. Mechanism and Machine Theory, 2011, 46(12): 1869—1887.

[6] 宋軼民, 張 俊, 張 君, 等. 3K-II型直齒行星齒輪傳動的固有特性[J]. 機械工程學報, 2009, 45(7): 23—28.

Song Yimin, Zhang Jun, Zhang Jun, et al. Inherent characteristics of 3K-Ⅱ spur planetary gear trains[J]. Chinese Journal of Mechanical Engineering, 2009, 45(7): 23—28.

[7] 楊富春, 周曉君, 鄭津洋. 復式行星齒輪傳動系統綜合動力學模型及振動特性研究[J]. 振動與沖擊, 2011, 30(8): 144—148.

Yang Fuchun, Zhou Xiaojun, Zheng Jinyang. Dynamic model and vibration characteristics of complex compound planetary gear set[J]. Journal of Vibration and Shock, 2011, 30(8): 144—148.

[8] 劉振皓, 巫世晶, 王曉筍, 等. 基于增量諧波平衡法的復合行星齒輪傳動系統非線性動力學[J]. 振動與沖擊, 2012, 31(3): 117—122.

Liu Zhenhao, Wu Shijing, Wang Xiaosun, et al. Nonlinear dynamics of compound planetary gear sets based on incremental harmonic balance method[J]. Journal of Vibration and Shock, 2012, 31(3): 117—122.

[9] 巫世晶, 劉振皓, 王曉筍, 等. 基于諧波平衡法的復合行星齒輪傳動系統非線性動態特性[J]. 機械工程學報, 2011, 47(1): 55—61.

Wu Shijing, Liu Zhenhao, Wang Shaosun, et al. Nonlinear dynamic characteristics of compound planetary gear train sets based on harmonic balance method[J]. Chinese Journal of Mechanical Engineering, 2011, 47(1): 55—61.

[10] 羅玉濤, 陳營生. 混合動力兩級行星機構動力耦合系統動力學建模及分析[J]. 機械工程學報, 2012, 48(5): 70—75.

Luo Yutao, Chen Yingsheng. Dynamic modeling and analysis of power coupling system with two-stage planetary gear trains for hybrid system[J]. Chinese Journal of Mechanical Engineering, 2012, 48(5):70—75.

[11] 馬 銳, 陳予恕. 含裂紋故障齒輪系統的非線性動力學研究[J]. 機械工程學報, 2011, 47(21): 84—90.

Ma Rui, Chen Yushu. Nonlinear dynamic research on gear system with cracked failure[J]. Chinese Journal of Mechanical Engineering, 2011, 47(21):84—90.

[12] 王 鑫, 徐玉秀, 武寶林, 等. 兩級定軸齒輪斷齒故障的非線性耦合特性研究[J]. 振動與沖擊, 2016, 35(13): 119—124.

Wang Xin, Xu Yuxiu, Wu Baolin, et al. Coupled nonlinear characteristic of a two-stage gear system with chipping fault[J]. Journal of Vibration and Shock, 2016, 35(13): 119—124.

[13] Li G, Li F, Wang Y, et al. Fault diagnosis for a multistage planetary gear set using model-based simulation and experimental investigation[J]. Shock and Vibration, 2015, 2016: 1—19.

[14] Liang X, Zuo M J, Pandey M. Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set[J]. Mechanism and Machine Theory, 2014, 76: 20—38.

[15] Liang X, Zuo M J, Hoseini M R. Vibration signal modeling of a planetary gear set for tooth crack detection[J]. Engineering Failure Analysis, 2015, 48: 185—200.

[16] Liang X, Zuo M J, Liu L. A windowing and mapping strategy for gear tooth fault detection of a planetary gearbox[J]. Mechanical Systems and Signal Processing, 2016, 80: 445—459.

[17] 王世宇, 宋軼民, 沈兆光, 等. 行星傳動系統的固有特性及模態躍遷研究[J]. 振動工程學報, 2005, 18(4): 412—417.

Wang Shiyu, Song Yimin, Shen Zhaoguang, et al. Research on natural characteristics and loci veering of planetary gear transmissions[J]. Journal of Vibration Engineering, 2005, 18(4): 412—417.