精設(shè)題組 八大途徑破解圓錐曲線離心率范圍
廣東
溫伙其
(作者單位:廣東省廣州市第十六中學(xué))
精設(shè)題組 八大途徑破解圓錐曲線離心率范圍
廣東
溫伙其
離心率是圓錐曲線重要幾何特征之一,各種教材都會詳細介紹,但對離心率范圍問題甚少闡述.近年高考全國卷對離心率的取值范圍的考查已成為高頻考點和重點.本文通過設(shè)置題組的形式,歸納了八種常見解決離心率取值范圍的途徑,探討解題的思路與要點,供讀者參考.
題組一 函數(shù)法,即構(gòu)造離心率的函數(shù)關(guān)系式,借助值域求范圍

【解題分析】


【解題要點】
1.根據(jù)題設(shè)條件,如曲線的定義、等量關(guān)系等建立離心率和其他一個變量的函數(shù)關(guān)系式;
2.確定函數(shù)的定義域及單調(diào)性;
3.利用函數(shù)求值域的方法求解離心率的范圍.
題組二 角度法,即借助角的大小(鈍角、銳角、直角)構(gòu)造a,b,c齊次不等關(guān)系
1.如圖,橢圓的中心在坐標原點O,頂點分別為A1,A2,B1,B2,焦點分別為F1,F(xiàn)2,延長B1F2與A2B2交于P點,若∠B1PB2為鈍角,則此橢圓的離心率的取值范圍是________.
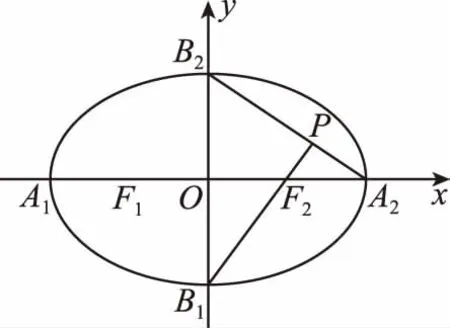

【解題分析】
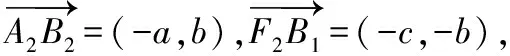


【解題要點】
1.鈍角可得向量的數(shù)量積大于0;
2.銳角可得向量的數(shù)量積小于0;
3.直角三角形則有直角邊小于斜邊;
4.根據(jù)上述大小關(guān)系整理為關(guān)于a,b,c的齊次不等式,轉(zhuǎn)化為離心率的不等式.
題組三 條件法,即借助條件的不等關(guān)系,構(gòu)造a,b,c的齊次不等式

【解題分析】


【解題要點】
1.找出題目本身給出的不等條件,如已知某些量的范圍,線段的長度,面積的取值等;
2.把上述的量用a,b,c表示;
3.整理得離心率的不等關(guān)系式,從而求解.
題組四 三邊大小法、均值定理法和性質(zhì)法,構(gòu)造a,b,c齊次不等關(guān)系

【解題分析】


【解題要點】
1.三角形兩邊之和大于第三邊,三角形兩邊之差小于第三邊;
4.把上述大小關(guān)系整理為關(guān)于a,b,c的齊次不等式,轉(zhuǎn)化為離心率的不等式.
題組五 圖象法,即借助特殊圖象特征構(gòu)造a,b,c齊次不等關(guān)系


【解題分析】



【解題要點】
1.圓和圓錐曲線的交點數(shù)量問題,即為它們的位置關(guān)系問題,作圖可尋找a,b,c和半徑大小的關(guān)系;
2.直線和雙曲線的交點問題,即為它們的位置關(guān)系問題,作圖可得的直線斜率和漸近線斜率大小的關(guān)系;
3.把上述大小關(guān)系整理為關(guān)于a,b,c的齊次不等式,轉(zhuǎn)化為離心率的不等式.
題組六 有解成立法,即把存在性(有解)和恒成立問題轉(zhuǎn)化為函數(shù)最值
1.題目同題組五第1題.
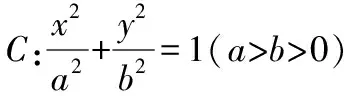
【解題分析】


【解題要點】
1.函數(shù)m=f(x)有解,即不等式f(x)min≤m≤f(x)max成立;
2.函數(shù)m≥f(x)恒成立,即不等式m≥f(x)max成立;
3.函數(shù)m≤f(x)恒成立,即不等式m≤f(x)min成立;
4.把上述大小關(guān)系整理為關(guān)于a,b,c的齊次不等式,轉(zhuǎn)化為離心率的不等式.
題組七 位置關(guān)系法,即利用點在曲線內(nèi)(外)部建立離心率不等式

【解題分析】
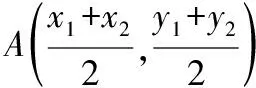
【解題要點】


3.把上述大小關(guān)系整理為關(guān)于a,b,c的齊次不等式,轉(zhuǎn)化為離心率的不等式.
題組八 判別式法,即轉(zhuǎn)化為a,b,c齊次方程解的數(shù)量問題
1.題目同題組五第1題.
2.題目同題組七第2題.
【解題分析】


【解題要點】
1.直線與圓錐曲線的交點問題,聯(lián)立方程后,轉(zhuǎn)化為一元二次方程的求判別式問題;
2.直線與雙曲線的交點在同一支(在不同的兩支)問題,轉(zhuǎn)化x1·x2的符號問題;
3.把上述問題整理為關(guān)于a,b,c的齊次不等式,轉(zhuǎn)化為離心率的不等式.

(作者單位:廣東省廣州市第十六中學(xué))
 教學(xué)考試(高考數(shù)學(xué))2018年4期
教學(xué)考試(高考數(shù)學(xué))2018年4期
- 教學(xué)考試(高考數(shù)學(xué))的其它文章
- 高三數(shù)學(xué)一輪復(fù)習(xí)必須重視的幾個環(huán)節(jié)
- 璐瑜初成 尚需雕琢
——“超級全能生”2018年高考全國卷26省3月聯(lián)考試題反饋征稿 - 原創(chuàng)之旅,需在聯(lián)考的土壤中成長
——“超級全能生”全國卷26省4月份聯(lián)考的思考 - 高考全國卷《三角函數(shù)與解三角形》命題規(guī)律分析與展望
- “超級全能生”2018年高考全國卷26省3月聯(lián)考甲卷數(shù)學(xué)(文科)
- “超級全能生”2018年高考全國卷26省3月聯(lián)考甲卷數(shù)學(xué)(理科)
