淺談中學(xué)數(shù)學(xué)教學(xué)中的德育功能

廣東省廣州市第七中學(xué) (510080) 陳世明

十九大報(bào)告指出，要落實(shí)立德樹(shù)人的根本任務(wù)，“才者，德之資也；德者，才之帥也”．教育部最新(2017年8月17日)發(fā)布的《中小學(xué)德育工作指南》中又指出：“充分發(fā)揮課堂教學(xué)的主渠道作用，將中小學(xué)德育內(nèi)容細(xì)化落實(shí)到各學(xué)科課程的教學(xué)目標(biāo)之中，融入滲透到教育教學(xué)全過(guò)程”．“嚴(yán)格落實(shí)德育過(guò)程．按照義務(wù)教育、普通高中課程方案和標(biāo)準(zhǔn)，上好道德與法治、思想政治課，落實(shí)課時(shí)，不得減少課時(shí)或挪作它用”．“發(fā)揮其它課程德育功能．要根據(jù)不同年級(jí)和不同課程的特點(diǎn)，充分挖掘各門(mén)課程蘊(yùn)含的德育資源，將德育內(nèi)容有機(jī)融入到各門(mén)課程教學(xué)中”．“數(shù)學(xué)、科學(xué)、物理、化學(xué)、生物等課要加強(qiáng)對(duì)學(xué)生科學(xué)精神、科學(xué)方法、科學(xué)態(tài)度、科學(xué)探究能力和邏輯思維能力的培養(yǎng)，促進(jìn)學(xué)生樹(shù)立勇于創(chuàng)新、求真求實(shí)的思想品質(zhì)”．在中學(xué)數(shù)學(xué)教學(xué)中如何挖掘、滲透德育功能，是當(dāng)今數(shù)學(xué)教學(xué)中值得研究的一個(gè)課題，本文對(duì)此做初步探討，敬請(qǐng)各位專家指教！

1．在定理教學(xué)中培養(yǎng)學(xué)生求真求實(shí)的思想品質(zhì)

眾所周知，邏輯性、嚴(yán)謹(jǐn)性、抽象性是數(shù)學(xué)學(xué)科的三大特征．為了降低學(xué)習(xí)難度，新課程中對(duì)許多定理的證明不作要求，然而，我們?cè)诮虒W(xué)中發(fā)現(xiàn)，許多老師在教學(xué)此類定理時(shí)，不僅既不講此類定理的證明也不探究此類定理的生成過(guò)程，而且對(duì)此類定理為真所必要的說(shuō)明也只字不提，只是將此類定理中的一些關(guān)鍵字詞抽出來(lái)“一填了之”，然后就是大規(guī)模的定理應(yīng)用(筆者所在區(qū)的一次區(qū)公開(kāi)課上，授課老師就是這樣處理的)．事實(shí)上，按新課程標(biāo)準(zhǔn)，對(duì)此類定理不要求證明，并不等于不作說(shuō)明，若對(duì)此類定理為真所必要的說(shuō)明也沒(méi)有了，那么數(shù)學(xué)就變成了一門(mén)不講理的學(xué)科了，這樣的數(shù)學(xué)教學(xué)不僅失去了對(duì)學(xué)生求真求實(shí)的思想品質(zhì)的培養(yǎng)良機(jī)，而且也是十分危險(xiǎn)的！“直線與平面平行的判定定理”是空間直線與平面的位置關(guān)系的第一個(gè)定理，新課標(biāo)教材對(duì)這一定理的證明不作要求，筆者在教學(xué)這一定理時(shí)是這樣處理的：

師：要判定直線a與平面α平行，只要判定——

生：直線a與平面α沒(méi)有公共點(diǎn)．

師：那如何判定直線a與平面α沒(méi)有公共點(diǎn)呢？(學(xué)生一臉茫然，不知所措！大約1分鐘后)

師：不好辦吧！請(qǐng)同學(xué)們回憶一下，我們已經(jīng)知道直線a與“α”一定是沒(méi)有公共點(diǎn)的？(大約1分鐘后)

生1：直線a與和它異面的直線b一定是沒(méi)有公共點(diǎn)的或直線a與和它平行的直線b也一定是沒(méi)有公共點(diǎn)的！

師：很好！這樣一來(lái)，我們不妨大膽的來(lái)猜一猜：若直線a與平面α內(nèi)的一條直線b異面，能否推出直線a與平面α沒(méi)有公共點(diǎn)？

生(部分)：能吧？

生(部分)：不能！

師：生2你來(lái)說(shuō)一說(shuō)為什么不能？

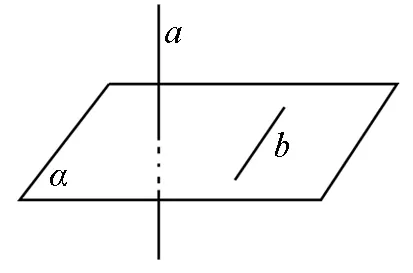
圖1

生2：這很簡(jiǎn)單，舉一個(gè)反例就成了！如圖1，a與b是異面直線，但a與α有公共點(diǎn)．

師：真妙！要否定一個(gè)結(jié)論，只要舉一個(gè)反例就成了．同學(xué)們清楚了嗎？

生：清楚了！

師：若直線a與平面α內(nèi)的一條直線b平行呢？又能否推出直線a與平面α沒(méi)有公共點(diǎn)？(巡堂發(fā)現(xiàn)：同學(xué)們?cè)诋?huà)各種圖形，也想舉一個(gè)反例來(lái)否定上述結(jié)論，但均沒(méi)有成功，大約2分鐘后)

生：能！(很肯定的)

師：為什么？

生：沒(méi)有找到反例！

師：沒(méi)有找到反例就能說(shuō)明直線a與平面α沒(méi)有公共點(diǎn)？假若那樣的反例大家都沒(méi)有找到呢？

生：是啊！

師：因此，要肯定一個(gè)結(jié)論，一定要說(shuō)明理由才行！生3，你來(lái)說(shuō)說(shuō)理由看？

圖2

生3：還沒(méi)想好！(其余同學(xué)在積極思考)

師：如圖2，由a∥b，可推出什么結(jié)論？

生3：過(guò)a,b可確定一個(gè)平面β．

師：很好!大家看，在確定了平面β后，直線a與平面α就“天各一方”(學(xué)生大笑)！但它們并不“孤單”(學(xué)生又笑)，因?yàn)棣僚cβ有一條公共直線b相連，真所謂“天各一方——一線牽”啊！這樣一來(lái)，要說(shuō)明直線a與平面α沒(méi)有公共點(diǎn)，只要說(shuō)明——

生：直線a與直線b沒(méi)有公共點(diǎn)即可！而a∥b，所以直線a與直線b沒(méi)有公共點(diǎn)，從而直線a與平面α沒(méi)有公共點(diǎn)，故a∥α．

師：太好了！這樣一來(lái)，我們就得到了一個(gè)什么結(jié)論？

生：如果直線a與平面α內(nèi)的一條直線b平行，那么直線a與平面α平行．

圖3

師：如圖3，也能推出a∥α嗎？

生(恍然大悟的)：不能！

師：沒(méi)想到吧！前述結(jié)論應(yīng)修改為——

生：如果平面外的一條直線與平面內(nèi)的一條直線平行，那么這條直線與這個(gè)平面平行．

師：很好！這就是我們今天要學(xué)的“直線與平面平行的判定定理”(下面的課從略)．

在上述定理的生成過(guò)程中，從學(xué)生熟知的“直線a與和它異面的直線b一定是沒(méi)有公共點(diǎn)或直線a與和它平行的直線b也一定是沒(méi)有公共點(diǎn)”出發(fā)，通過(guò)“猜想——實(shí)驗(yàn)(畫(huà)圖)——概括”等過(guò)程，比較自然的得出結(jié)論．尤其是通過(guò)“天各一方——一線牽”的“藝術(shù)化”處理后，定理為真的事實(shí)已一目了然，對(duì)定理是否再需證明已不是很重要了．

所謂“求真”，就是“求是”，亦即實(shí)事求是去認(rèn)識(shí)事物本質(zhì)，把握事物的規(guī)律；“求實(shí)”則是在對(duì)這種規(guī)律的指導(dǎo)下，去做、去實(shí)踐．一個(gè)數(shù)學(xué)定理往往需經(jīng)合情推理的發(fā)現(xiàn)，再經(jīng)演繹推理的證明才能獲得，尤其是課本中不要求證明的定理，其證明往往是比較復(fù)雜的，教學(xué)中，通過(guò)揭示此類定理的生成過(guò)程，對(duì)培養(yǎng)學(xué)生求真求實(shí)的科學(xué)態(tài)度，培養(yǎng)和鍛煉學(xué)生的探究能力和思維品質(zhì)有更大的作用和意義．

2．在公式教學(xué)中鍛煉學(xué)生科學(xué)探究能力和創(chuàng)新意識(shí)

李克強(qiáng)總理最近(2018年1月3日國(guó)務(wù)院常務(wù)會(huì)議)突出強(qiáng)調(diào)理論數(shù)學(xué)等基礎(chǔ)學(xué)科對(duì)于原始創(chuàng)新能力的重要意義，他還指出“數(shù)學(xué)等基礎(chǔ)學(xué)科研究要著眼于未來(lái)，但必須從教育抓起”．中學(xué)數(shù)學(xué)教學(xué)任重道遠(yuǎn)，同時(shí)也倍受鼓舞，在中學(xué)數(shù)學(xué)教學(xué)中，培養(yǎng)和鍛煉學(xué)生科學(xué)探究能力、邏輯思維能力和創(chuàng)新能力的例子很多，尤其在公式教學(xué)中．這里僅舉一例：

師：有一天，甲同學(xué)來(lái)問(wèn)我這樣一個(gè)問(wèn)題：cos15°=cos(60°-45°)=cos60°-cos45°為什么不對(duì)？說(shuō)實(shí)話，甲同學(xué)還很不錯(cuò)，知道這一等式是不成立的，同學(xué)們你們是否也知道？

生：知道！

師：為什么？說(shuō)說(shuō)理由看？

生：因?yàn)閏os15°>0，而cos60°-cos45°<0，所以等式不成立．

師：很好！這樣一來(lái)，我們達(dá)成了一個(gè)共識(shí)：cos(60°-45°)≠cos60°-cos45°．那么cos(60°-45°)究竟等于多少呢？(學(xué)生陷入沉思中！)

師：cos(60°-45°)是一個(gè)三角函數(shù)問(wèn)題，在前面第一章我們已學(xué)習(xí)了三角函數(shù)的有關(guān)知識(shí)，能否有公式可用？

生：好像沒(méi)有！

師：除了前面第一章我們已學(xué)習(xí)了三角函數(shù)的有關(guān)知識(shí)外，我們還學(xué)過(guò)其它的三角函數(shù)知識(shí)沒(méi)有？

生：在初中還學(xué)過(guò)解直角三角形！

師：好的！既然在第一章的三角函數(shù)里沒(méi)有公式可用，那么，我們不妨就到直角三角形中去看一看！你能否畫(huà)出一個(gè)角為60°的直角三角形？

生：太容易了！

圖4

師：是嗎？那我就來(lái)畫(huà)一個(gè)RtΔABC，使得∠A=60°,∠C=90°，如圖4，在這個(gè)RtΔABC中，你還能作出一個(gè)45°，同時(shí)還出現(xiàn)15°的角嗎？

生1：很好辦！以A為頂點(diǎn)，AB為一邊，在RtΔABC中作∠BAD=45°交BC于D，則∠DAC=15°．

師；你真行！在這個(gè)直角三角形中，能否得出cos15°呢？

生2：很簡(jiǎn)單！在RtΔACD中，AC=ADcos15°．

師：在RtΔABC中，還可得出AC=？

生2：AC=ABcos60°．

師：這樣就有ADcos15°=ABcos60°．現(xiàn)在要求cos15°，若在這一等式的右邊也出現(xiàn)AD，那么，兩邊同約去AD，即可求出cos15°，下面怎樣才能使等式的右邊也出現(xiàn)AD呢？(學(xué)生又陷入沉思中！大約2分鐘后)

生3：老師，可不可以這樣做？

師：怎么做？請(qǐng)講！

生3：(生3口述，老師板書(shū))在圖4中，過(guò)D作DE⊥AB于E，則由ADcos15°=ABcos60°得：ADcos15°=(AE+BE)cos60°=ADcos45°cos60°+BEcos60°=ADcos45°cos60°+DEcot30°cos60°=ADcos45°cos60°+ADsin45°cot30°cos60°,所以cos15°=cos45°cos60°+sin45°cot30°cos60°.

師：太妙了！(這時(shí)教室里響起了熱烈的掌聲，同學(xué)們也有大功告成之感！)上述結(jié)果完全是正確的，但形式太“丑”了，說(shuō)得不好聽(tīng)一點(diǎn)，簡(jiǎn)直是“丑不可言”！(學(xué)生感到很突然，教室里立即鴉雀無(wú)聲)，你們看，等式右邊的第一項(xiàng)是二項(xiàng)積，而第二項(xiàng)則是三項(xiàng)積，不和諧吧！更“可惡”的是：左邊實(shí)際上是cos(60°-45°)，只與60°,45°有關(guān)，與30°無(wú)關(guān)，而右邊的第二項(xiàng)竟然冒出一個(gè)30°，這個(gè)“30°”豈不是來(lái)添亂嗎？

生4：那就把它化掉吧！

師：好的，生4，你來(lái)試試！

生4：(上臺(tái))通過(guò)化簡(jiǎn)得出：cos(60°-45°)=cos60°cos45°+sin60°sin45°①

師：等式①的確優(yōu)美多了！當(dāng)然①式也還不太和諧——

生：左邊是“-”，而右邊是“+”．

師：很好！這也正好說(shuō)明世上并沒(méi)有“十全十美”的事物(到此，同學(xué)們松了一口大氣，大有洋洋得意之感！)，這時(shí)——

師：你們別高興太早！剛才甲同學(xué)是將cos15°化成cos(60°-45°)，我們幫他解決了；

若乙同學(xué)是將cos15°化成cos(45°-30°)，而丙同學(xué)是將cos15°又化成cos(135°-120°)呢？…，我們是不是一一幫他們?nèi)ソ鉀Q？

生：不！

師：那怎么辦？總不能“見(jiàn)死不救”吧！

生5：讓他們自己按上述方法去解決．

生6：老師，我們能否得出一個(gè)一般的公式？免得每次都這樣去做，太煩了！

師：這個(gè)想法好！得出一個(gè)怎樣的公式？

生6：是否對(duì)任意的α,β∈R，都有cos(α-β)=cosαcosβ+sinαsinβ②

師：很好！你是怎樣想到的？

生6：我是根據(jù)上述①式猜出來(lái)的！

師：真不錯(cuò)！不過(guò)，猜出來(lái)的結(jié)論不一定正確，你能證明它成立嗎？

生6：還沒(méi)有想好！

師：好的！請(qǐng)繼續(xù)思考．有誰(shuí)能證明②式？(同學(xué)們?cè)诜e極思考，大約1分鐘后)

師：能否仍按前面作直角三角形的方法去證？

生：不能？

師：為什么？

生：因?yàn)棣?β不一定能成為直角三角形的一個(gè)內(nèi)角．

師：很對(duì)，不過(guò)不要否定得太快！雖然現(xiàn)在不能作直角三角形了，但前面的那種證法中所用的思想方法說(shuō)不定還有用呢！所以不能“過(guò)河拆橋”，要學(xué)會(huì)“感恩”！下面我們一起來(lái)反思上述解法的關(guān)鍵點(diǎn)在哪里(與學(xué)生一起反思上述解法的每一步)．

師：生7，你來(lái)說(shuō)一說(shuō)上述解法的關(guān)鍵點(diǎn)在哪里？

生7：算兩次！就是把“AC”算了兩次，第一次得出AC=ADcos15°，第二次得出AC=ABcos60°，這樣就得出了關(guān)于cos15°的一個(gè)方程，然后通過(guò)解方程就得出了cos15°，也就是cos(60°-45°)的值．

師：說(shuō)得太好了！上述解法實(shí)際上應(yīng)用了“算兩次”的思想方法，你們還在哪里也用到過(guò)這一思想方法？

生：在《平面向量》里也用過(guò)．

師：對(duì)啊！“算兩次”是一種重要的解題思想方法，不僅過(guò)去用到，現(xiàn)在用到，而且將來(lái)還可能用到！下面再回到②式的證明，怎樣才能證明它呢？

生8：老師！是不是還是用“算兩次”？

師：怎么算？

生8：還沒(méi)想好！

師：請(qǐng)?jiān)傧胍幌耄姓l(shuí)想到了嗎？(大約1分鐘后)

師：前面說(shuō)了，在第一章三角函數(shù)里已沒(méi)有公式可用，又不能用作直角三角形的方法，那怎么辦？換句話說(shuō)，現(xiàn)在進(jìn)是進(jìn)不了了，進(jìn)不了就——

生：退！

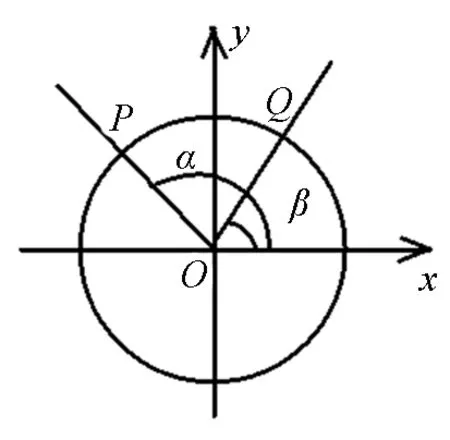
圖5

師：退到什么地方去呢？這是一個(gè)三角函數(shù)問(wèn)題吧！那三角函數(shù)是從什么地方出發(fā)的？

生：?jiǎn)挝粓A！退到單位圓中去．

師：好的！那就到單位圓中去看一看，如圖5，在單位圓中，設(shè)α,β的終邊與單位圓分別相交于P,Q兩點(diǎn)，由三角函數(shù)的定義得P(cosα,sinα),Q(cosβ,sinβ)，請(qǐng)大家觀察②式的右邊，它恰是——

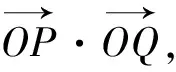
師：那②式的左邊等于——

從而有cos(α-β)=cosαcosβ+sinαsinβ．

生：原來(lái)如此！

師：果然又用到“算兩次”！但③式一定正確嗎？

生：正確！

生10：還不一定吧？

師：為什么？

師：好極了！遇事要冷靜，不要被一時(shí)的成功沖昏頭腦，考慮問(wèn)題應(yīng)全面，接下來(lái)該怎么辦？

生：分情況討論！(這里從略)

師：這樣一來(lái)，我們就證明了②式，有了這一公式，要算兩角差的余弦就很方便了，這一公式也就是我們今天要學(xué)習(xí)的“兩角差的余弦公式”(下面的課從略)．

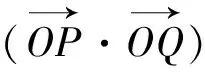
公式是構(gòu)成整座數(shù)學(xué)大廈的支柱之一，加強(qiáng)對(duì)公式的探究教學(xué)，不僅是新《數(shù)學(xué)課程標(biāo)準(zhǔn)》對(duì)我們每位老師的要求，也是培養(yǎng)創(chuàng)新型人才、提高教學(xué)質(zhì)量的必由之路．

3．在解題教學(xué)中塑造學(xué)生誠(chéng)信做人、理性做事的優(yōu)良品德

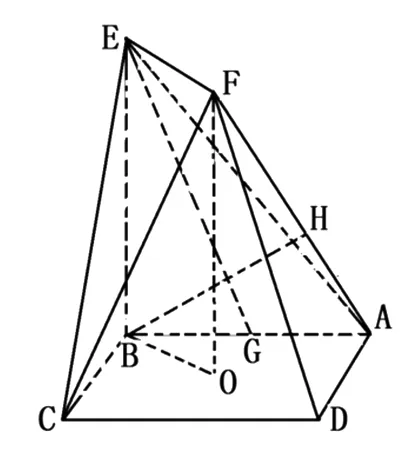
圖6

此題在用向量法求解的過(guò)程中有一個(gè)關(guān)鍵步驟，就是求出點(diǎn)A和F的坐標(biāo)后，根據(jù)條件計(jì)算點(diǎn)H的坐標(biāo)．筆者當(dāng)時(shí)是用“近朱者赤近墨者黑”來(lái)提示學(xué)生直接寫(xiě)出H點(diǎn)的坐標(biāo)的，在得到筆者的提示后，學(xué)生很容易地理解了筆者所要表達(dá)的意圖，問(wèn)題很快解決．通過(guò)這個(gè)例子和經(jīng)過(guò)筆者的進(jìn)一步提示，學(xué)生對(duì)傳統(tǒng)文化中的“中庸之道”有了更加理性的認(rèn)識(shí)，上例中的點(diǎn)H的坐標(biāo)不能用中點(diǎn)坐標(biāo)公式簡(jiǎn)而求之，而是在類比中點(diǎn)坐標(biāo)公式“取得平衡”的思想中將兩端點(diǎn)的坐標(biāo)各取一定的比例系數(shù)來(lái)求得．中庸并非“正中間”，而是不偏不倚的“中”，做人之道便是至誠(chéng)至信、公平待人．在解題教學(xué)中，要讓學(xué)生既領(lǐng)悟到數(shù)學(xué)的知識(shí)與方法，也更加理性地體會(huì)到中國(guó)傳統(tǒng)文化中關(guān)于做人的道理，一舉兩得．

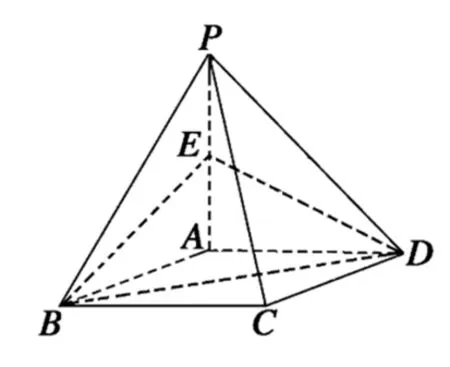
圖7

要求出SΔBDE，由已知條件，應(yīng)“腳踏實(shí)地”地去計(jì)算出ΔBDE的三邊長(zhǎng)，而當(dāng)算出ΔBDE的三邊長(zhǎng)后，“奇跡”發(fā)生了，原來(lái)ΔBDE為直角三角形，從而問(wèn)題簡(jiǎn)單獲解．

“機(jī)會(huì)是留給有準(zhǔn)備的人的”，本題中，若沒(méi)有前期“腳踏實(shí)地”地計(jì)算的準(zhǔn)備，就沒(méi)有后來(lái)簡(jiǎn)單獲解的機(jī)會(huì)．在這里“求距離”是最終目標(biāo)，為了實(shí)現(xiàn)這個(gè)目標(biāo)，我們必須先“腳踏實(shí)地”地進(jìn)行計(jì)算和推理，這一思維正是我們做許多事情時(shí)應(yīng)有的方法和態(tài)度．

在數(shù)學(xué)的發(fā)生與發(fā)展過(guò)程中，知識(shí)的形成與演變、重要思想方法的確立與發(fā)展、重大理論的發(fā)現(xiàn)與沿革等，其本身充滿著唯物辯證法的思想．而在高中的數(shù)學(xué)教學(xué)中，面對(duì)一群理性精神的形成正處于關(guān)鍵期的高中學(xué)生，教學(xué)中盡可能多地發(fā)揮數(shù)學(xué)的學(xué)科特性，通過(guò)培養(yǎng)理性思維與分析問(wèn)題、解決問(wèn)題的能力培養(yǎng)學(xué)生誠(chéng)信做人與理性做事．同時(shí)，在塑造學(xué)生正確的人生觀、世界觀和價(jià)值觀及用理性的思維看待事物時(shí)，使學(xué)生更深刻地理解數(shù)學(xué)的方法和理論，讓學(xué)生更加主動(dòng)地端正學(xué)習(xí)態(tài)度，提高數(shù)學(xué)能力．德育與數(shù)學(xué)教學(xué)相輔相成，本身也是一個(gè)辯證的關(guān)系．