風險條件下研發項目改進DEA選擇模型
谷曉燕,何 鋒
(1.北京信息科技大學信息管理學院,北京 100192;2.北京航空航天大學電子信息工程學院,北京 100191)
1 引言
研發項目是企業生存和發展的動力,研發項目選擇是對一個復雜的多因素投資系統進行邏輯分析與綜合判斷的過程,是項目管理中最重要和最復雜的問題之一[1-3]。相對于普通工程項目,研發項目的高創新性使其具有更大的不確定性,這種不確定性不僅表現在項目本身的技術因素,還表現在項目之外,比如市場的不確定性、競爭對手的出現等[4]。風險的存在使研發項目的合理選擇更加具有挑戰性。而且,由于研發項目周期長、投資大,關系到企業的競爭優勢和未來增長,是否能選擇適合企業戰略的研發項目,應對研發過程的風險,將影響到企業若干年的發展。因此,對于風險條件下研發項目的選擇開展研究,具有重要的理論和實踐意義。
近年來,對研發項目選擇的研究總體上可以分為兩類,一類為研發項目投資組合選擇,一類為研發項目排序。對于項目投資組合的研究,主要方法為:專家打分[5]、單目標或多目標規劃[6-7]、多準則決策[8-9]、蒙特卡羅模擬[10-11]、人工神經網絡[12]、交叉熵[13]、經濟概率[14]和數據包絡分析(Data Envelopment Analysis,DEA)[15]等。對于研發項目排序的研究,主要方法為:網絡層次分析法(Analytic Network Process,ANP)[16]、混合整數規劃[17]和DEA[18]等。本文的研究著眼于研發項目排序。
在以上方法中,DEA由于本質是相對最優性,可以對同類型決策單元進行相對有效性評價[19-21],適用于具有多投入、多產出的研發項目選擇。DEA首次由運籌學家 Charnes,Cooper和Rhodes[22]于1978 年正式提出,是評價多指標投入和多指標產出決策單元相對有效性的多目標決策方法,是一種以效率為基礎的非參數統計方法,被廣泛應用于評價具有多維評價指標結構的同質決策單元相對效率。針對研發項目,少量學者用DEA進行項目選擇和排序的研究,如Chang等[15]提出了一種DEA、背包公式和模糊集理論集成的模型,該模型解決在資源有限情況下,選擇能實現組織目標的項目組合問題,特別是當備選項目有模糊的輸入和輸出數據時。Karasakal等[18]提出基于DEA的多準則計分方法進行研發項目選擇,采用區間層次分析法(Analytic Hierarchy Process,AHP)得到準則的權重區間,并以此作為模型的保證域(AssuranceRegion, AR)約束,在DEA的基礎上,構建了一個具有兩層門限的評估模型。張秀峰等[23]基于三階段DEA方法,對研發項目的研發效率進行評價。陳光宇等[24]構建了組織層和項目層兩層次影響因素,結合系統動力學DEA和超效率DEA對項目進行效率排序。國內外學者在研發項目效率評價方面做出了有益的探索,但在用DEA進行研發項目選擇時也存在部分不足,如:DEA導致許多決策單元都是有效的,缺乏辨識度;不合適的權重賦值導致與現實情況不符合或與決策者的判斷相矛盾等;缺乏對研發項目的戰略特征和風險的整體分析。
本文基于實物期權理論,綜合考慮研發項目面臨的風險,根據研發項目的投入產出情況,基于DEA的基本思想,考慮企業戰略,利用平衡計分卡(Balanced Score Card,BSC)理念約束權重的變化范圍,改進DEA模型,對備選研發項目進行排序,提出了一種基于效率排序的研發項目選擇模型,從而實現對研發項目的選擇。
2 研發項目改進DEA選擇模型
研發項目的高不確定性帶來了高風險,主要體現在三個方面:技術風險、突發風險和市場風險。市場風險為研發項目未來潛在現金流大小的不確定性,技術風險為技術的不確定性所帶來的影響,突發風險為突發事件對研發項目現金流的影響[25]。
根據企業戰略,研發項目各評價指標的相對重要程度不同,在評價時需要將權重變化的信息引入到DEA方法中,構建存在保證域的研發項目DEA選擇模型。BSC是把企業及其內部各部門的任務和決策轉化為多樣的、相互聯系的目標,然后再把目標分解成多項指標的多元業績評價系統。本文基于BSC的思想,把企業戰略引入DEA模型,為同屬于一個計分卡下的投入分配權重的變化范圍。
2.1 模型變量
為了實現對一個企業內部多個研發項目的選擇,本文設置了如下變量:
(1)備選研發項目包含多個投入,如人、財、物等。設企業對N個研發項目進行選擇,每個研發項目包含m個投入,用xij表示。其中,下標j表示第j個研發項目,下標i表示第j個研發項目的第i個投入,對于研發項目的每個投入來說,都不可能小于0,因此有xij≥0,1≤j≤N,1≤i≤m。
(2)備選研發項目包含多個產出:如現金流、社會效益等。設每個研發項目包含n個產出,用ysj表示,其中的下標j表示第j個研發項目,下標s表示第j個研發項目的第s個產出,對于研發項目的每個產出量來說,都不可能小于0,因此有ysj≥0,1≤j≤N,1≤s≤n。
(3)對于研發項目,不同的投入具有不同的權重,用vi表示,其中下標i表示第i個投入,vi≥0,1≤i≤m。
(4)本文結合BSC理念,規定同屬于一個計分卡下的所有投入的比例和占整個投入權重和的比例只能在一定范圍內進行變化。假設評價系統中一共有P個計分卡,第p(1≤p≤P)個計分卡有qp個投入,而該計分卡占整個計分卡的權重范圍是:
(ap,bp),0≤ap≤1,0≤bp≤1,ap≤bp則有:
(1)
(5)對于研發項目,不同的產出具有不同的權重,用us表示,其中下標s表示第s個產出,本文不對產出加以權重約束,us≥0,1≤s≤n。
(6)對于不同的研發項目,可能具有不同的研發周期,用Tj表示,其中下標j表示第j個研發項目。
(7)不同的研發項目,成功的可能性也可能有區別。一般來說,越是基礎的研究,成功概率越小,越是應用的研究,成功可能性越大。研發項目具有的研發成功概率用qj表示,其中下標j表示第j個研發項目。
(8)研發項目成功后能為企業帶來的現金流入有一個估計值;研發項目失敗后能回收的殘值,也有一個估計值,殘值可以為0,也可以大于0。殘值大于0的項目,表明雖然研發項目失敗,但是其中的某些技術已經被攻克,或者其中的某些研發途徑是正確的,產生的經驗或者實體可以用到企業其它的項目中,從而使該項目具有一定的殘值。
設對于成功的研發項目,能為企業帶來的現金流為Vj,對于失敗的研發項目,能回收的殘值為Cj。
(9)在本文中,假定每個項目預計的貼現率一致為R,同時市場無風險利率一致為r。
2.2 研發項目選擇模型
為了構建風險條件下研發項目選擇模型,首先結合期權的理念,考慮資金的時間價值,計算帶有期權價值的研發項目現金流。
按照NPV(Net Present Value,凈現值)的方法,可以得到折算到投資開始時的項目價值,為:
(2)
把研發項目階段成功狀態看作是實物期權中的上漲狀態,把研發項目階段失敗狀態看作是實物期權中的下跌狀態。因此,可以得到研發項目的上漲幅度和下跌幅度,如下式所示:
(3)
按照無套利均衡的思想,可以構造出風險中性概率,使用風險中性概率計算資產未來收益的期權值。根據Ross[26]嚴格的證明,盡管現實世界里的投資者在風險偏好方面存在差異,但是風險中性假設下得到的期權估值同樣可以應用于非風險中性的情況。因為當出現套利機會時,投資者無論風險偏好如何都會采取套利行為,從而使消除套利機會后的均衡價格與投資者的風險偏好無關。
風險中性概率計算公式如下:
(4)
在得到風險中性概率的基礎上,根據二叉樹期權理論,可以得到研發項目期權價值為:
(5)
因此,折合到階段開始時刻包含期權的項目價值為:
NPVOPj=Ej+Sj
(6)
在得到包含期權的研發項目價值后,可以將這個值作為產出值的一部分進行項目選擇。在DEA中,效率是指投入與產出的比例。實現DEA思想的基本模型為C2R模型[27]。按照C2R模型,可以計算每個研發項目的有效性,用hj表示。
(7)
當hj=1時,研發項目投資有效;當hj<1時,研發項目投資無效。但是,標準C2R模型給不出研發項目有效性的排序。

(8)

(9)


vi≥0,us≥0,(1≤i≤m,1≤s≤n)
(10)
3 算例分析


表1 研發項目關鍵參數
為了能夠對所提出的模型進行計算和驗證,本文利用MatLab7.0設計了相應的算法,實現了對5個研發項目的對比,根據C2R模型,也設計了相應的算法。
觀察5個項目的關鍵參數,每個項目的成功概率、研發周期、成功后能為企業帶來的現金流,以及項目失敗后的殘值都不相同。利用期權的思想,可以計算研發項目帶有期權的潛在現金流,克服了僅僅以項目最終現金流作為產出的不足。
對于本算例中的5個項目,其計算后的投入產出矩陣為:

(11)

h1=0.58839
h2=1
h3=1
h4=0.66671
h5=0.94195
(12)

(13)
按照本文提出的模型,5個研發項目的可投資性排序為:
(14)
所以,選擇研發項目的順序為:
(15)
(16)
(17)
4 敏感性分析


(18)

本文將研發項目成功概率變化對研發項目3相對于研發項目2的優勢的影響結果進行分析計算,結果如圖1所示。

圖1 項目成功概率影響

同樣,本文統計和分析第一個投入量改變對研發項目效率的影響,如圖2所示。

圖2 第一個投入x1影響
當修改研發項目2和研發項目3第二個投入量的值時,本文同樣能夠得到類似的結論,其分析結果如圖3所示。

圖3 第二個投入x2影響
當修改研發項目2和研發項目3第三個投入量的值時,其分析結果圖如圖4所示。
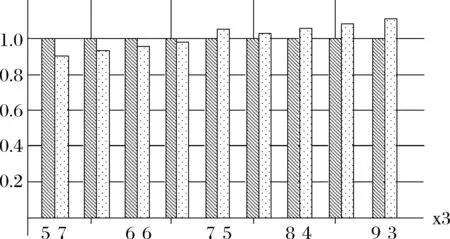
圖4 第三個投入x3影響
可以看出,無論是改變第一個投入量,還是第二個投入量,或者第三個投入量,本文提出的模型相對于標準DEA模型具有更好的參數敏感度,能夠正確給出各個研發項目的相對優勢變化過程。對于該算例,研發項目之間的相對優勢對第一個投入量更敏感。
5 結語


