滾筒輸送線路徑規劃方法研究*

薛志強,游有鵬

(南京航空航天大學 機電學院，江蘇 南京 210016)

0 引 言

滾筒輸送線是由電動滾筒、光電傳感器、控制器、條碼識別模塊等設備組成的一種傳輸系統，由于其具有可定制化、空間利用率高、成本低等優勢，被廣泛用于物品分揀、生產線連接和物流系統集成等場合[1]。

目前，滾筒輸送線的部件已逐漸標準化，從而形成了更高集成度的滾筒輸送機，包括直線兩方向傳送輸送機、圓弧兩方向傳送輸送機、直角四方向移載輸送機、兩方向升降輸送機和斜坡輸送機等功能模塊。升降輸送機和斜坡輸送機使得輸送線可能存在三維多層結構；而直角移載輸送機模塊擁有4個方向的傳輸移載功能，是輸送線中的重要節點模塊，使輸送線更加柔性化。

隨著現代物流系統的發展，需求更加復雜化、多樣化，滾筒輸送線系統面臨較多的挑戰。一條輸送線中各個輸送機之間構成復雜的拓撲關系，需要特殊的數據結構來描述。在復雜輸送線結構中，從某入口到某出口可能會出現多條路徑，不同路徑根據傳送距離、傳送時間和一定的約束等存在優劣之分。如何選擇最優的可行輸送路徑，是本文要解決的路徑規劃問題。目前，國內外關于輸送線路徑規劃方法的研究，主要基于網格法劃分的環境模型，運算量較大、實時性較差[2]。

本文將以滾筒輸送線為對象，構建其環境模型并進行優化，充分考慮輸送線系統中的實際影響因素，引入路徑規劃算法，解決滾筒輸送線中的路徑選擇問題。

1 輸送線結構環境模型

1.1 輸送線結構建模

滾筒輸送線的模塊之間需建立連接關系，才能形成完整且流通的輸送線，完成相應的功能。這里采用有向圖的數據結構來構建輸送線復雜連接，用鄰接矩陣為圖結構的儲存方式。

假定輸送線有n個模塊，構成圖G=(V,E)的n個頂點，即V={v0,v1,...,vn-1}，圖的鄰接矩陣是一個n×n的二位數組，用A[n][n]表示，且數組的元素為：

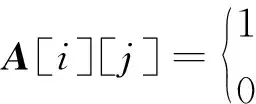
(1)

式中：A[i][j]=1—模塊i和模塊j之間有連接，且連接方向為從模塊i指向模塊j；A[i][j]=0—模塊i和模塊j無任何方向的連接。

上述無加權的有向圖能準確描述滾筒輸送線的結構，便于上位機圖形繪制、動態監控等，也易于實現較少模塊輸送線的路徑規劃。但對于模塊數量較大、連接較復雜的輸送線，基于上述圖結構模型進行路徑規劃變得較為困難，需要對上述建模方法進行適當改進。

1.2 滾筒輸送線結構模型改進

針對滾筒輸送線的特點與路徑規劃需求，可以對上述圖結構模型進行適當的簡化與改進。事實上，滾筒輸送線中只有移載輸送機模塊可以完成3個或4個方向的路徑選擇；作為入口或出口的輸送機模塊是整個輸送線的結構邊界；而其他模塊只具有傳輸功能，相互連接路徑唯一，不存在路徑選擇。

根據上述特點，本文將以入口、出口、3個或4個方向的移載輸送機作為節點，節點之間的其他輸送機連接作為加權路徑，對輸送線圖結構進行簡化。

在重新構建的輸送線圖結構中，節點與節點之間可能存在多種不同類型輸送機連接組合，進而形成一條路段通道，路段長度計算方法成為首要解決的問題。

本文采用輸送機當量來衡量路徑長度，計算方法如下：

(2)

式中：Qij─從i節點到j節點路段上的輸送機當量；m─輸送機類型總數；k(1,2,3…,m)─輸送機類型標號；qk─該路徑上第k類輸送機的數量；fk─第k類輸送機的當量換算系數。

各類輸送機當量換算系數如表1所示。

表1 各類輸送機當量換算系數

本研究以直線傳送輸送機為參考基準進行取值，具體可根據實際情況進行調整。

輸送機當量換算系數取值方法：在相同條件下，多次測試、計算并統計物品通過各類輸送機所用時間與通過直線傳送輸送機所用時間的比值，以各類輸送機對應的比值數據的平均值為其相應的當量換算系數。

某一較復雜輸送線結構簡化后的例圖如圖1所示。

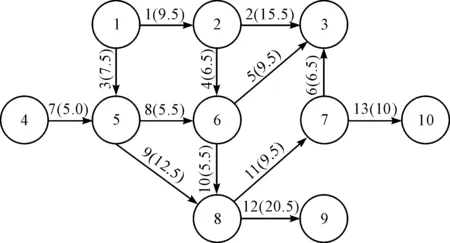
圖1 輸送線結構簡化例圖

近100個輸送機模塊的輸送線，簡化后僅有10個節點。該圖結構中節點集合為{①，②，③，④，⑤，⑥，⑦，⑧，⑨，⑩}，路段集合為{1,2,3,4,5,6,7,8,9，10，11，12，13}，箭頭所指為節點間路段上的物品傳送方向。節點①、④為入口節點，節點③、⑨、⑩為出口節點，其他節點都為移載模塊節點，從而構成6組路徑規劃需求。圖1中，各個路段號后括號內的數字為對應路段的輸送機當量。

如從節點⑧到節點⑨的路段12中，輸送機當量為20.5，其計算方法如下：假設路段12包含15個直線傳送輸送機、2個直角移載輸送機、1個180度圓弧傳送輸送機、1個升降輸送機，則依據式(2)得其輸送機當量為：15×1+2×0.5+1×1.5+1×3=20.5。

按照上述方法對復雜輸送線的結構模型改進后，再建立有向圖結構，鄰接矩陣中的值為各個路段的輸送機當量，節點自身的輸送機當量為0，節點之間無直接連接的輸送機當量為無窮大。

采用這種改進的結構模型可簡化圖結構和路徑規劃的難度，因此下文路徑選擇優化算法的設計將以此為基礎。

2 輸送線的路徑規劃

2.1 基于Dijkstra算法路徑選擇優化設計

輸送線的功能是將物品從特定的入口送入，經過一定的路徑送達特定的出口。為了提高輸送能力，需要獲取從特定入口到特定出口的最短路徑。

Dijkstra算法是求解單源最短路徑規劃的經典算法[3-4]，將其用于輸送線的最短路徑規劃的流程如圖2所示。

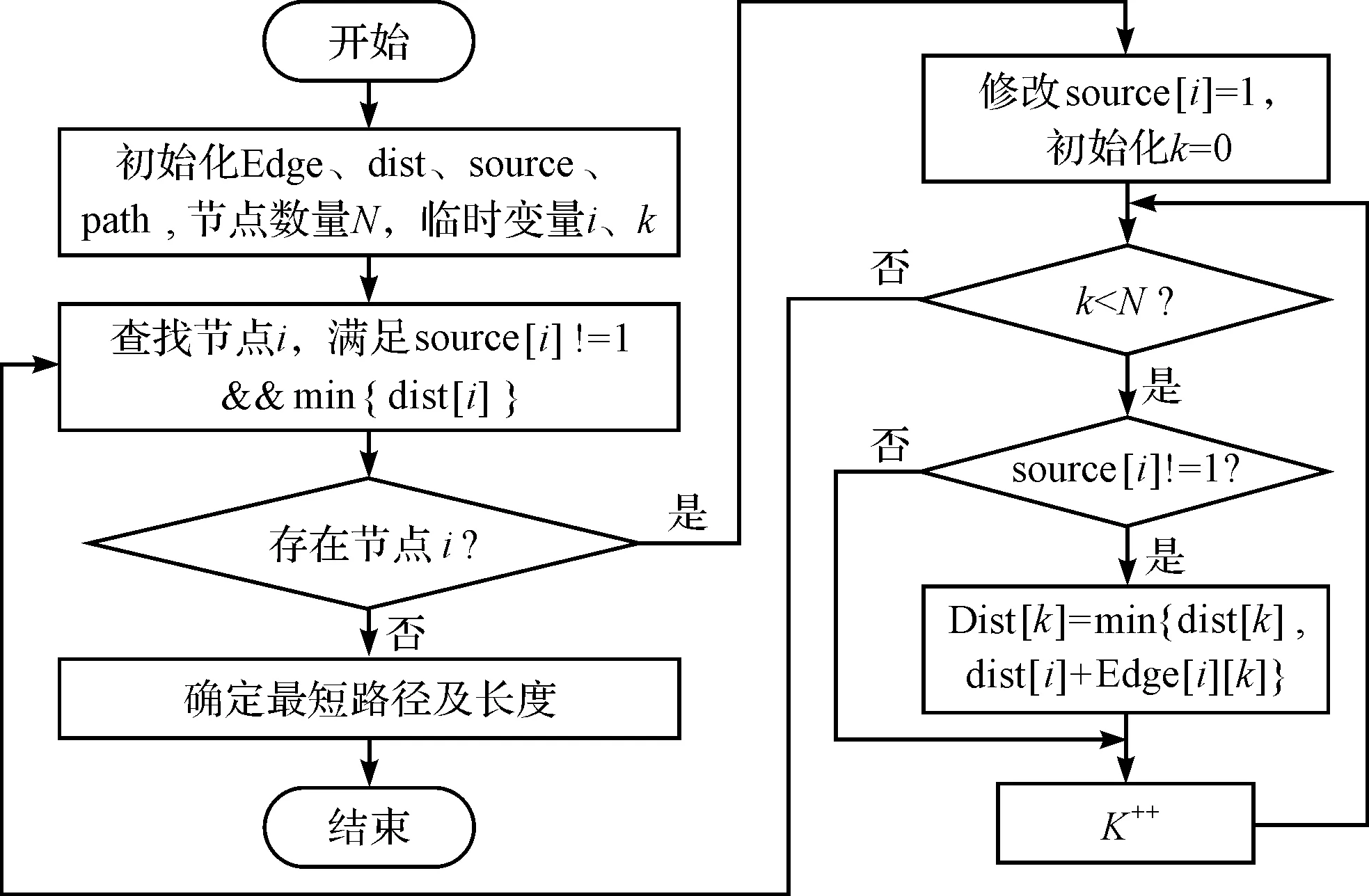
圖2 迪杰斯特拉算法求解輸送線最短路徑流程圖

以圖1為例，假定需計算從入口①到出口⑩的最短路徑，首先建立圖結構鄰接矩陣所對應的二維數組Edge[10][10]。

為求解最短路徑及長度，需要設置并計算3個一維數組：數組dist[10]表示當前從節點①到其他節點的最短路徑長度(初始值為Edge中的第一行)；數組source[10]表示當前節點是否已被檢測(0為未檢測，1位已檢測，初始時候只有節點①對應的值為1，其他都為0)；數組path[10]表示從節點①到某節點的最短路徑上該節點的前一個節點序號，最后可以采用倒向追蹤法來確定最短路徑上的各個節點[5-6]。

對于規模較小的圖結構，應用Dijkstra算法求解輸送線的最短路徑較方便；而當簡化后的圖結構仍然比較復雜時，啟發式智能算法則具有更好的實時性和魯棒性。

2.2 基于蟻群算法的路徑選擇優化設計

蟻群算法是依據螞蟻種群總是能找從巢穴到食物之間的最短路徑而提出的一種啟發式算法，不僅與輸送線的最短路徑模型類似，而且具有良好的實時性，便于實現動態路徑規劃。

蟻群算法中路徑選擇含有貪心規則的不利因素，引入選擇概率來避免完全貪心規則而陷入局部最優，而啟發函數對路徑選擇概率有較大的影響。通常，傳統蟻群算法采用距離啟發函數ηij(t)=1/dij，這種啟發函數容易使得螞蟻貪圖當前的一小步，進而選擇偏離目標方向的節點。依據輸送線圖結構的節點松散、路徑靜態等特點，對啟發函數進行改進，增加目標節點對選擇下一節點的影響，改進后的啟發函數如下：

(3)

式中：dij─節點i到節點j的路段長度；djg─節點j到目標節點g之間的路段長度。

將式(3)引入到蟻群算法中，得到螞蟻k在t時刻由節點i轉移到節點j的概率，如下式所示：

(4)

式中：τij(t)—t時刻在路段(i,j)上的信息量(初始狀態下各路徑上的信息量都相等，為常數)；α—信息素啟發因子(衡量信息量對是否選擇該路徑的影響程度)；β—期望啟發因子(衡量啟發信息對螞蟻選擇路徑的影響程度)；allowedk—螞蟻k可選擇節點的集合[7]。

當所有的螞蟻在輸送線圖結構上完成一次路徑選擇后，需要對各路徑上的信息素進行更新，即：

τij(t+n)=(1-ρ)·τij(t)+Δτij

(5)

(6)

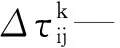
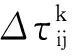
(7)

式中：Q—信息素加強系數；Lk—第k只螞蟻在本次迭代中所走過的路徑長度[8-9]。

根據輸送線圖結構的實際情況，本研究對蟻群算法中的參數進行取值，值的選擇因模型而異，需要不斷調整找到平衡點，進而求出最優路徑。

采用蟻群算法求解輸送線最短加權路徑及長度流程圖，如圖3所示。

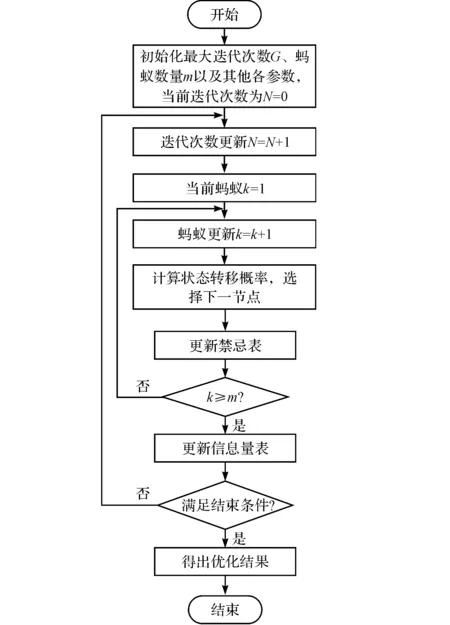
圖3 蟻群算法求解輸送線最優路徑流程圖

禁忌表用于記錄當前已知的不可能在最優路徑上的節點，信息量表用于記錄各個節點的信息素。

需要注意的是，盡管蟻群算法比Dijkstra算法更適合于規模較大的路徑規劃，且具有良好的實時性和魯棒性，但參數選擇不當仍能會影響求解。

2.3 實際工況約束下的輸送線路徑規劃策略

在裝配生產線等輸送線系統中，某些工況需要對最短路徑進行修正，主要歸納為以下兩類：

(1)某個物品必須經過輸送線中的某個節點進行特殊處理；

(2)當前最短路徑上某個路段通行壓力較大。

針對第一類情況，如果路徑必須包含某節點N，對2.1和2.2中的算法修正策略如下：先求解從起點到節點N的最短路徑及長度，再求解從節點N到終點的最短路徑及長度，最后進行拼接組合即可。該處理策略可以擴展應用于必須包含多個節點的路徑規劃問題。

針對第二類情況，如果當前搜索到的最短路徑上的路段P(i,j)較為擁堵，對2.1和2.2中的算法修正策略如下：可以根據擁堵的情況，通過適當的權數來增加路段P(i,j)的路段長度(Dijkstra算法中增加Edge[i][j]的值；蟻群算法增加dij的值)。這種處理策略可以增加選擇其他較通暢路徑的概率，進而達到最短路徑修正的目的[10-11]。

具體應用中，兩算法的選擇還需結合輸送線規模和算法的具體特點：規模較小的輸送線采用Dijkstra算法，規模較大的輸送線優先用蟻群算法；去蟻群算法無法求得最優路徑的情況下，再用Dijkstra算法重新求解。

2.4 實例分析

本研究以圖1所示系統為例，采用Dijkstra算法和蟻群算法分別求解圖1中從入口節點①到出口節點⑩的最優路徑，再加入2.3小節中兩種約束，對路徑重新規劃，分別得出最優結果，如表2所示(Dijkstra簡寫為Dij)。

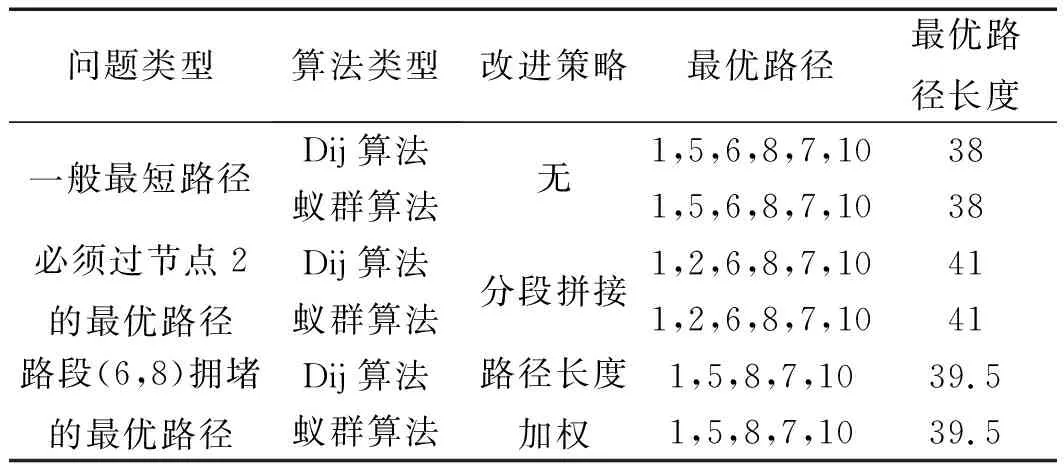
表2 輸送線最優路徑規劃算法結果驗證

由表2可知：兩種算法的求解具有相同的結果，且為實際最優路徑。

3 結束語

本文分析了滾筒輸送線的環境模型，提出了以輸送機當量衡量路徑長度的計算方法，并對較復雜輸送線的結構模型進行了改進。

研究的結果表明：

(1)改進后的結構模型簡化了圖結構，并降低了路徑規劃的難度；

(2)針對最短路徑選擇問題，分別采用較為經典的Dijkstra算法和啟發式的改進蟻群算法進行求解，分析了兩種算法的適用場合；

(3)針對輸送線應用的兩種實際工況，提出了相應的動態修正策略，為解決這兩類約束下滾筒輸送線路徑最優規劃提供了有效的解決方案，也可為其他類型輸送線的路徑規劃提供借鑒。