一種IGBT模塊的新型建模與瞬態仿真方法研究*

沈天浩，黃 瑞，楊 帆，陳俊玄，馮 權，洪文華，俞小莉*

(1.浙江大學 能源工程學院, 浙江 杭州 310000;2.上汽大眾汽車有限公司, 上海 201805)

0 引 言

在電動汽車開發的前期，需要對電池、電機、電控進行選型與匹配。IGBT模塊是電控的關鍵部件，選擇合適的IGBT模塊對電動汽車電控模塊的設計至關重要。

IGBT在工作過程中會產生損耗導致其溫度升高。IGBT模塊由封裝好的IGBT芯片和FWD(續流二極管)芯片組成。結溫是電子設備中半導體芯片PN結的工作溫度，當結溫過高時會導致硅材料芯片性能降低，乃至永久損壞。據統計，由溫度過高引起的IGBT失效占全部的55%以上[1]。電動汽車設計前期只能采用仿真的方法對IGBT模塊進行結溫預測，分析不同工況下的發熱與模塊結溫是否符合要求。

通過仿真對IGBT模塊的結溫進行預測是國內外研究的重點。姚芳[2]、宋飛[3]和陳彥[4]搭建了IGBT模塊的熱電聯合仿真模型，得到IGBT與FWD的損耗波形和結溫波形，但其僅針對一維模型，未進行三維流固耦合仿真，無法得到溫度場分布；陳清[5]和王淑旺[6]對某IGBT模塊進行散熱分析，得到其溫度場和流場分布，但其僅計算穩態工況，未計算瞬態結溫。

IGBT模塊工作時，其芯片發熱會隨時間作周期性波動，芯片的結溫也隨之周期性變化。目前的IGBT模塊仿真方法包括一維和三維仿真，但無法同時得到IGBT模塊的結溫分布云圖和結溫波動數據。

本文以型號為FS800R07A2E3的IGBT模塊為例，提出一種新型IGBT模塊仿真方法。

1 損耗計算

IGBT模塊在運行時會產生損耗，損耗主要包括IGBT芯片和FWD芯片的損耗，是IGBT模塊中的熱源。

1.1 損耗計算理論

三相橋式整流電路如圖1所示。

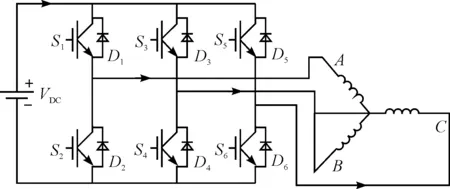
圖1 三相橋式整流電路

每相包含兩個IGBT芯片和兩個反向并聯的續流二極管(FWD)，二者工作時經歷周期性的開關狀態并產生損耗。

IGBT芯片的主要損耗是通態損耗[7]和開關損耗[8]，IGBT的通態損耗是由于其正向導通壓降產生的，其開關損耗是因為在開通和關斷的瞬間，電流和電壓有重疊期；FWD芯片的主要損耗是通態損耗和關斷損耗，FWD的通態損耗也是由于其正向導通電壓而產生的，其開關損耗則是因為二極管的反向恢復特性。

目前，電動汽車大多采用SVPWM(空間矢量)調制方式，其損耗可以通過計算得到[9-10]。

IGBT輸出特性如圖2所示。

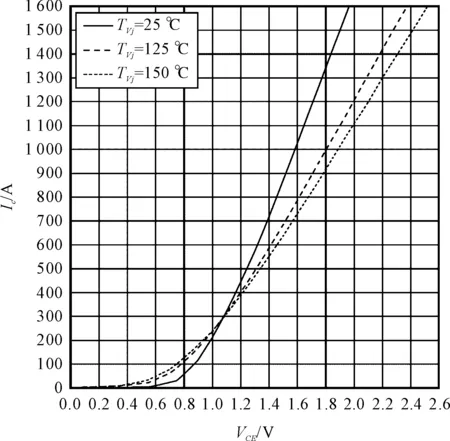
圖2 IGBT輸出特性

為了簡化損耗的計算，IGBT的導通壓降VCE與FWD的正向導通電壓VF與IC的關系可以近似用直線表示：

VCE(t)=VCE0+rCE*IC(t)

(1)

VF(t)=VF0+rF*IC(t)

(2)

式中：VCE0—IGBT門檻電壓；VF0—FWD門檻電壓；rCE—IGBT通態等效電阻；rF—FWD通態等效電阻。

當采用傳統7段SVPWM調制時，IGTB芯片和FWD芯片的損耗通過計算獲得。

(1)IGBT通態損耗。

(3)

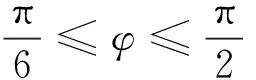
(4)

式中：IN—正弦波相電流幅值；M—調制比；φ—電流滯后電壓角度。

(2)IGBT開關損耗。

(5)

式中：fsw—開關頻率；Eon-nom—IGBT在標稱電壓Vnom和電流Inom下測得的開通損耗；Eoff-nom—IGBT在標稱電壓Vnom和電流Inom下測得的關斷損耗；VDC—直流電壓。

(3)FWD通態損耗。

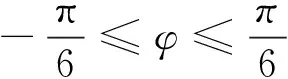
(6)

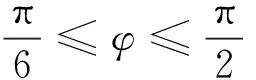
(7)

(4)FWD開關損耗。

(8)

式中：Erec-nom—FWD在標稱電壓Vnom和電流IF-nom下測得的反向恢復損耗。

由式(3～8)可得IGBT芯片和FWD芯片在一個相電流周期內的平均損耗，分別表示為：

PIGBT=Pcon_IGBT+Psw_IGBT

(9)

PFWD=Pcon_FWD+Psw_FWD

(10)

上式計算的是IGBT模塊工作時的平均損耗。三相橋式逆變電路的基本工作方式是180°導電方式，即每個橋臂的導電角度為180°，同一相(半橋)上下兩個臂交替導電，各相開始導電的角度依次相差120°。因此，一個IGBT橋臂在一個周期內只有一半時間是導通的。

IGBT芯片與FWD芯片的損耗是不規則的曲線，可以將兩者的損耗函數簡化為理想的半正弦波曲線。

兩者瞬態損耗的函數為：

(11)

(12)

式中：PIGBT(t)—IGBT芯片瞬態損耗；PFWD(t)—FWD芯片瞬態損耗；T—相電流周期。

1.2 FS800R07A2E3模塊損耗計算

1.2.1 穩態損耗

FS800R07A2E3模塊中IGBT芯片和FWD芯片的特征參數分別如表1、表2所示(特征參數測試條件為300 V，550 A，125 ℃)。

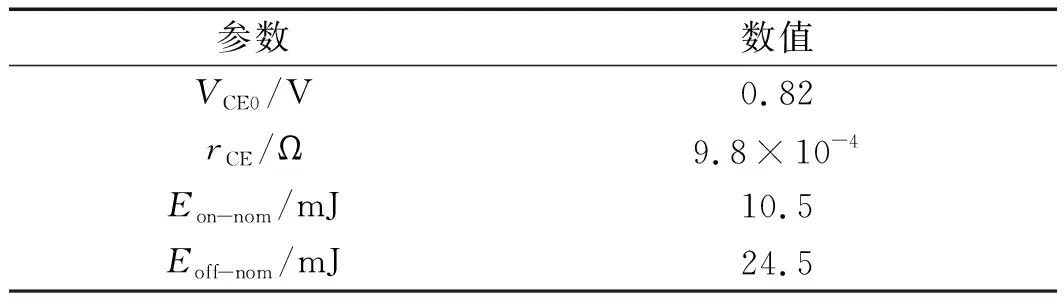
表1 FS800R07A2E3模塊IGBT芯片特征參數

表2 FS800R07A2E3模塊FWD芯片特征參數

IGBT模塊的部分工作參數如表3所示。

表3 FS800R07A2E3模塊工作參數

注：M—調制比；φ—電流滯后角；fsw—開關頻率；f0—相電流頻率

不同直流電壓VDC和相電流幅值IN工況下(工況1至工況3)，IGBT芯片與FWD芯片的平均損耗如表4所示。

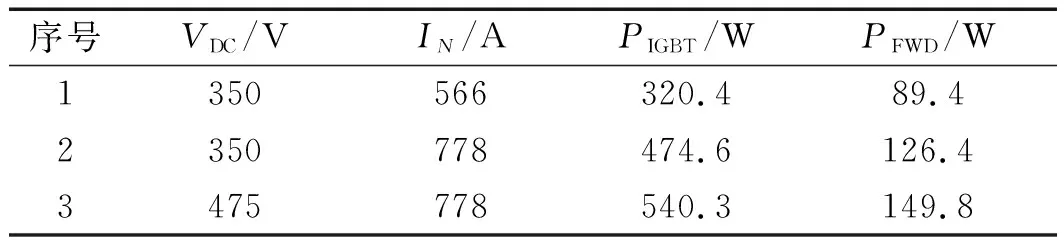
表4 不同工況下FS800R07A2E3模塊的損耗

由此可見：IGBT和FWD的平均損耗均隨VDC和IN的增大而增大。

1.2.2 瞬態損耗

本研究取工況1至3中發熱最大的工況3計算瞬態損耗。根據一個周期內平均損耗功率相同的原理進行等效，可知等效半正弦波的幅值為平均損耗的π倍。其他工況相同時，瞬態損耗的變化周期與相電流頻率有關。頻率為50 Hz時，瞬態損耗擬合式為：

(13)

(14)

IGBT模塊瞬態損耗曲線如圖3所示。

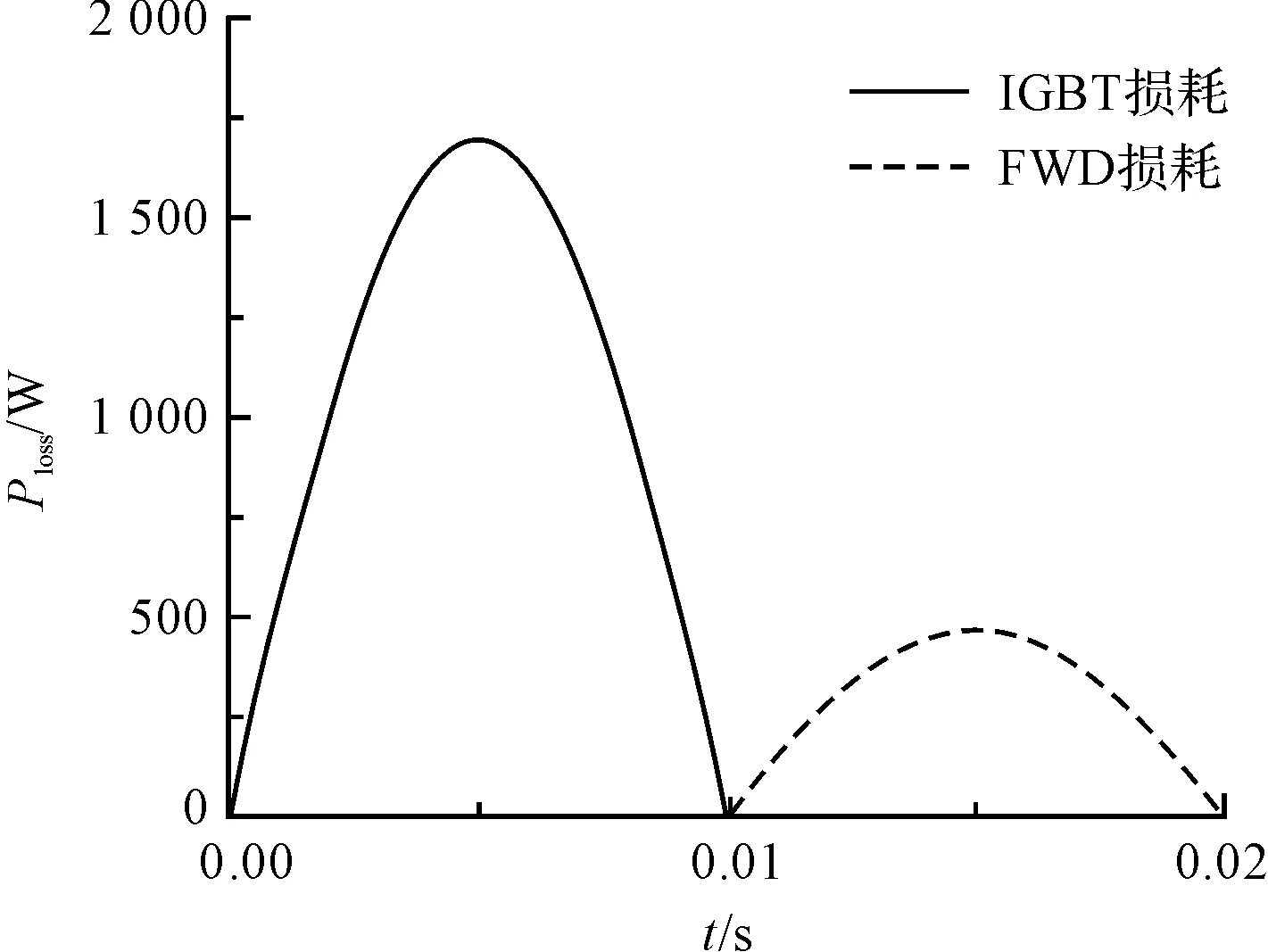
圖3 IGBT模塊瞬態損耗曲線

2 三維建模

在進行三維建模前，對IGBT模塊的三維模型做出以下假設：(1)芯片是一個均勻發熱體，芯片中所有層都是均勻的，無缺陷的；(2)芯片較薄，除了芯片截面法向外，其他表面均視為絕熱；(3)忽略輻射和空氣對流換熱；(4)冷卻液為不可壓縮流體且為湍流流動。

2.1 建模與網格劃分

本研究以英飛凌FS800R07A2E3模塊為例，建立其三維模型。通過測量及相關資料得到模塊的尺寸信息；采用SolidWorks建立模塊的三維模型并進行一定的簡化，去除密封圈槽，去除模塊內部的連接線等對散熱影響較小的結構；然后將IGBT幾何模型導入到HyperMesh中進行網格劃分，最小網格尺寸為0.1 mm。

三維模型和網格如圖4所示。

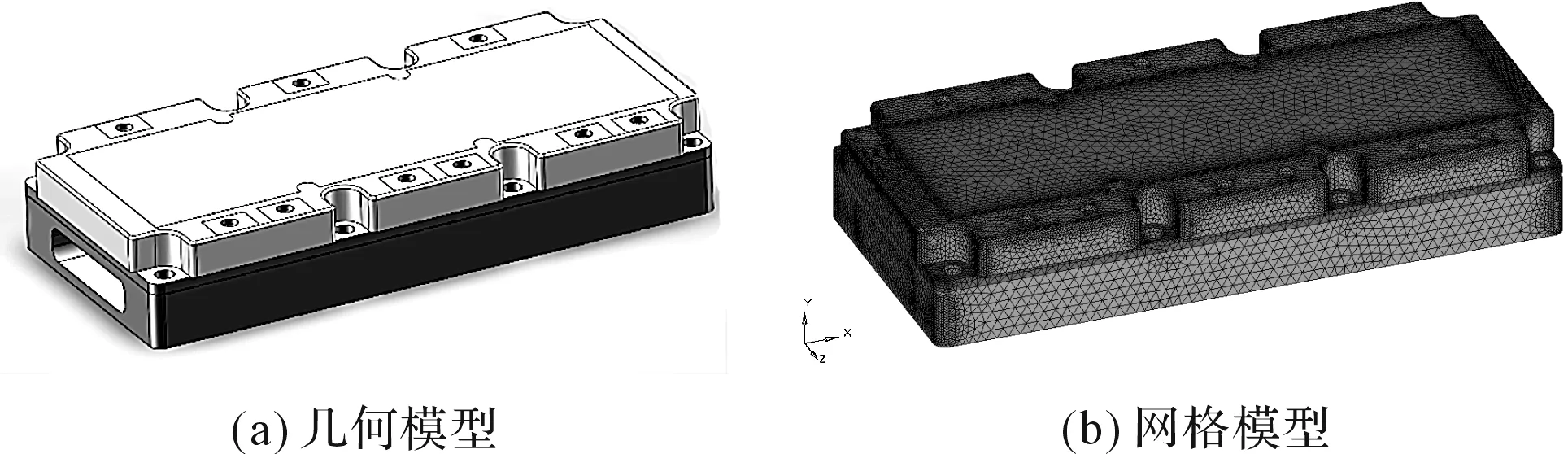
圖4 英飛凌FS800R07A2E3模塊模型

2.2 流固耦合計算模型

筆者采用Star-CCM+軟件對IGBT模塊進行瞬態三維流固耦合仿真，計算在不同工況、一定冷卻條件下的結溫分布和波動。

計算模型中的冷卻液為不可壓縮流體，滿足質量守恒、動量守恒、能量守恒方程，即:

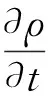
(15)

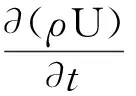
(16)

(17)

式中：ρ—流體的密度；U—速度矢量；p—流體壓力；μ—流體的動力學粘度；cp—流體的比熱容；λ—導熱系數；F—作用在流體上的質量力；q—流體所吸收的熱量；T—流體或固體溫度；Φ—能量耗散函數。

冷卻液在電機控制器中的流動為湍流，采用基于雷諾時均法的數值計算方法，引入湍流模型，計算中采用標準k-ε湍流模型，即：

(18)

(19)

式中：ui—U在i方向上的速度分量；k—湍動能；ε—耗散率；μt—湍流粘度；Gb—由浮生力產生的湍流動能；Gk—平均速度梯度引起的湍動能k的產生項；σk、σε—湍流普朗特數；C1ε，C2ε—經驗常數。

在Star-CCM+軟件中，流體域采用k-ε湍流模型，邊界層設置為2層。

2.3 物性參數設置

本研究，將HyperMesh中的面網格導入到Star-CCM+后，設置相應材料的物性參數。物性參數設置的對象包括內部芯片、外殼材料、導熱基板、冷卻液等，物性參數包括材料的密度、導熱系數、比熱容等。由于IGBT芯片的多層結構，網格密度無法細小至此，筆者采用復合導熱系數的計算方法對其進行折算[11]。

芯片材料為硅，基板材料為銅，外殼材料為工程塑料，冷卻液為50%水與50%乙二醇的混合物。

2.4 邊界條件設置

FS800R07A2E3模塊為三相全橋整流，每個全橋由兩個半橋組成，一個半橋由4個IGBT芯片和4個FWD芯片組成。半橋內部的實際結構和簡化三維模型如圖5所示。

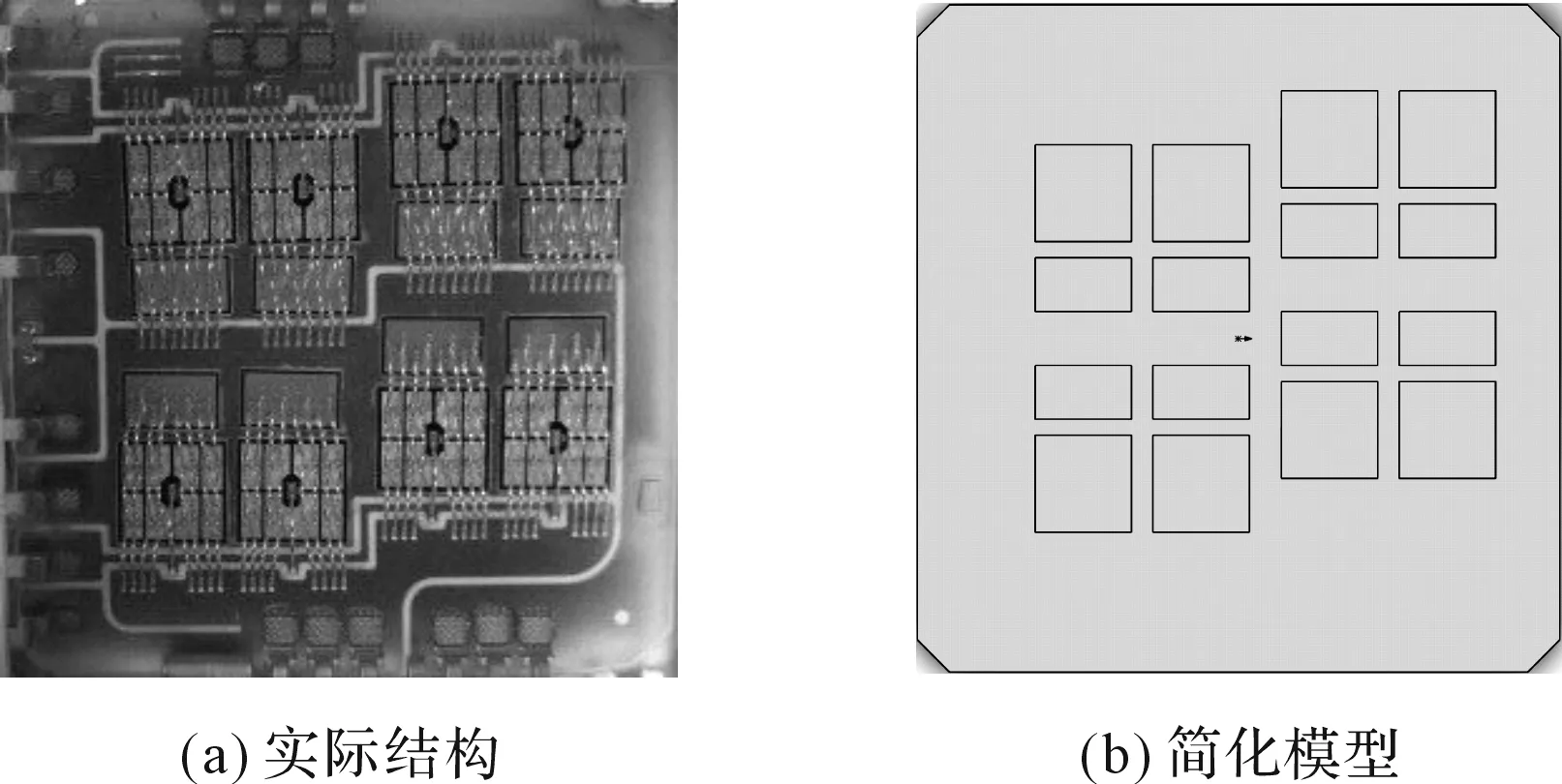
圖5 英飛凌FS800R07A2E3模塊半橋

本研究將上述IGBT和FWD芯片的發熱模型作為邊界條件，加載至三維模型，穩態加載為常數，瞬態加載為時間的函數。

電機控制器的入口溫度一般要控制在65 ℃以下，本文計算最惡劣工況，即冷卻液入口溫度為65 ℃，流量為10 L/min。

3 仿真結果

3.1 穩態仿真結果

本研究將上述穩態工況的發熱功率設定為邊界條件，對其進行仿真。在迭代500步以后仿真收斂，得到IGBT模塊的溫度分布云圖。流固耦合計算得到的溫度分布如圖6所示。

圖6 穩態仿真溫度分布云圖

圖6中，左側為冷卻液入口，右側為出口。定義冷卻液入口到出口分別為U/V/W相，U/V/W三相的最高溫度存在溫差，穩態下最高溫度出現在W相的IGBT芯片，最高結溫約為122 ℃。

各相芯片的最高溫度如表5所示。

表5 各相芯片最高溫度

三相溫度的不均勻性在2 ℃左右，分析其原因可能為U相靠近冷卻液入口，冷卻液溫度較低，因而帶走熱量較多。

3.2 實驗結果及分析

通過查閱數據表可以獲得不同冷卻液流速下的熱阻，結合冷卻液溫度和散熱功率，可以計算模塊的最高結溫。仿真數據與實驗數據對比如表6所示。

表6 三維仿真模型驗證

表6中，本文三維仿真模型得到的穩態仿真結果與廠家實驗數據之間的誤差在2%以內，驗證了三維模型的正確性。

3.3 瞬態仿真結果

在穩態計算中，W相遠離冷卻液入口，溫度最高，本文僅計算W相最高結溫波動。將上述瞬態損耗公式加載至W相，U相和V相的損耗仍采用穩態損耗加載。瞬態時間步設置為0.001 s，每個時間步包含50步迭代步數。由于從冷起動開始計算需要消耗大量計算資源和時間，因此將初始條件設置為穩態計算的結果。

由于瞬態熱源的周期性波動，W相IGBT芯片和FWD芯片的溫度也周期性波動。瞬態結溫波動數據如圖7所示。

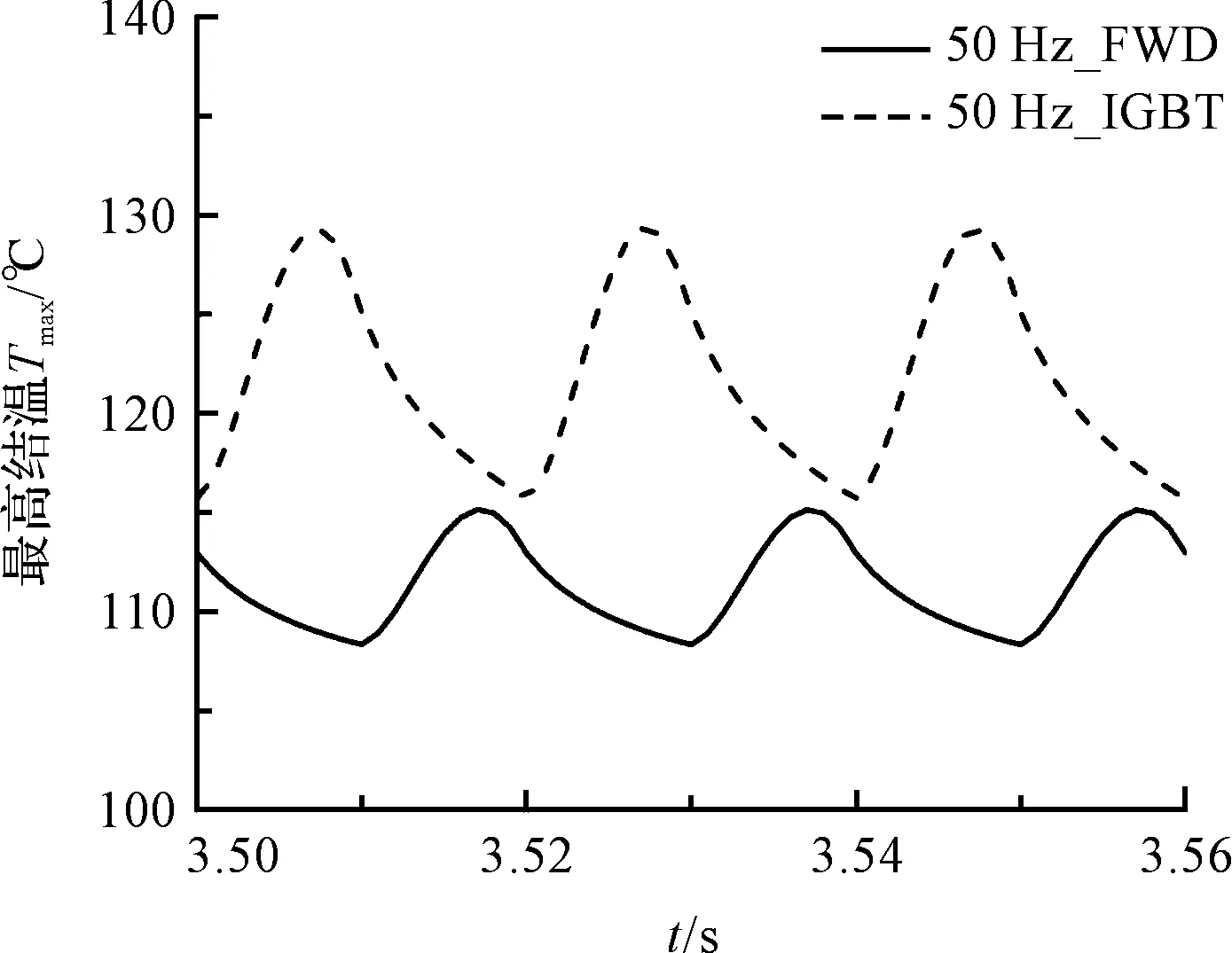
圖7 W相芯片結溫波動

圖7中，相電流頻率為50 Hz時，熱源的周期為0.02 s，結溫波動的周期也為0.02 s。在前三分之一周期內IGBT芯片溫度上升，后三分之二周期內溫度下降，最高結溫大約出現在周期的三分之一處。IGBT芯片的最高結溫達到129 ℃左右。

由于同一相中IGBT芯片溫度高于FWD芯片，本研究考察不同頻率下IGBT芯片的結溫波動。不同相電流頻率下IGBT芯片結溫變化如圖8所示。

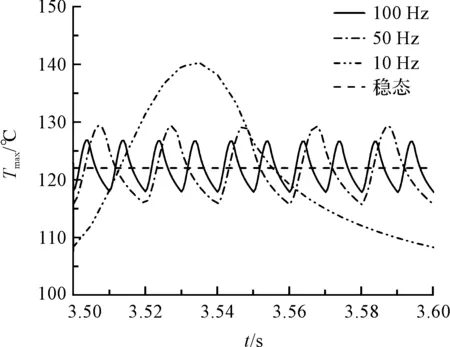
圖8 不同相電流頻率下結溫波動

圖8中，相電流頻率越高，最高結溫越低。可以解釋為：在芯片發熱的一個周期內，前部分周期芯片發熱，冷卻液帶走的熱量比發熱少，導致結溫升高；后部分周期內芯片不發熱，冷卻液持續帶走熱量，導致結溫降低。

4 結束語

本文以英飛凌FS800R07A2E3模塊為例，提出了一種新型的IGBT模塊的仿真方法,得到以下結論：

(1)IGBT模塊內部三相芯片的最高結溫存在2℃左右溫差，一維瞬態計算無法模擬三相間溫差與溫度分布云圖；

(2)IGBT模塊進行選型時，僅采用穩態仿真是不夠的，其結溫波動需要通過瞬態仿真得到；

(3)IGBT的實際結溫存在周期性波動，并且與相電流的頻率相關。在電機控制器設計階段，可以考慮采用提高頻率的方法以降低IGBT模塊的最高結溫；

(4)采用瞬態仿真和流固耦合結合的方法，既能仿真得到結溫分布云圖，也可以獲得結溫波動數據。