葉片中弧線的一種混合算法研究
方志陽,駱天舒,徐少杰,方 寅
(杭州汽輪機股份有限公司,浙江 杭州 310022)
0 引 言
透平葉片二維截面型線的中弧線是透平葉片氣動概念設計的出發點:透平葉片中弧線軌跡是構造葉片初始就要確定的數據,然后根據中心在中弧線上一系列內切圓半徑就可以給出葉片的延弦長方向分布的厚度,進而得到葉片二維截面型線;有了中弧線才可以給出進出氣角等數據,然后可以確定速度三角形。以上所述是正向設計的過程。
在逆向設計過程中,先有葉片二維截面型線數據,如果要得到進出氣角數據及速度三角形,就需要逆向求出中弧線數據,也就是葉片二維截面型線內部的一系列內切圓數據,一系列內切圓圓心就能構成和中弧線近似的插值曲線。以往的研究中有兩種傳統方法:陸啟韶[1]提出了一種逐次迭代方法來求葉片型線內切圓序列,徐旭嶺等[2-4]也采用了這種方法;LI等[5]提出了另一種不同的方法。但是這兩種傳統方法有一個共同的不足之處,即在前緣或尾緣附近很難得到內切圓。
針對以上問題,本文提出一種混合方法,即在葉片前緣和尾緣處利用最優化算法擬合出和前緣及尾緣型線最匹配的內切圓,而在葉片的其他部位使用前述的兩種傳統方法。
1 方 法
傳統方法1如圖1所示。
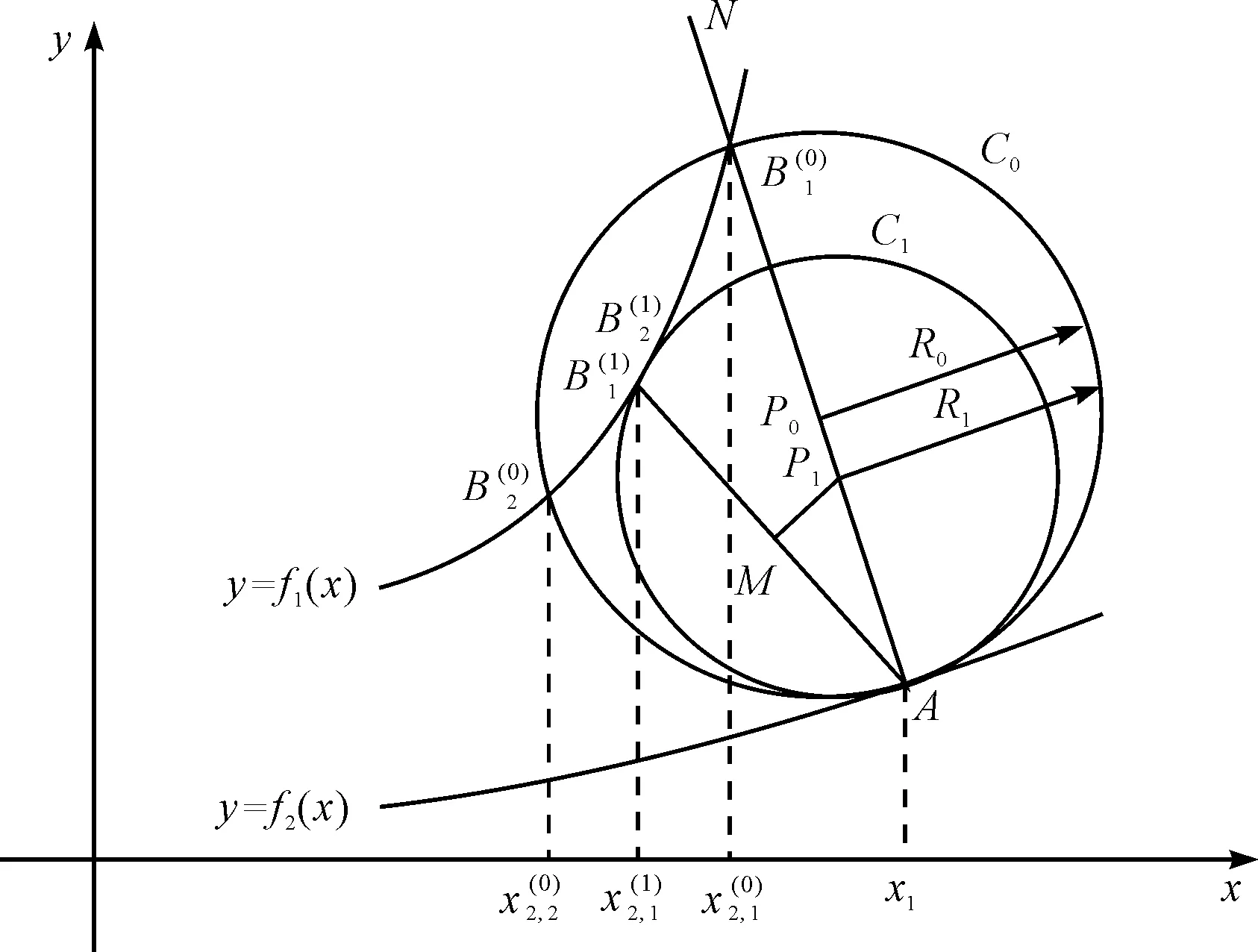
圖1 傳統算法1幾何演示
在傳統方法1中,一般葉片二維截面型線由壓力面型線和吸力面型線構成,其中一條型線由函數y=f1(x)描述,另一條型線表示為函數y=f2(x)。
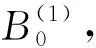

傳統方法2如圖2所示。

圖2 傳統算法2演示
在傳統方法2中,首先生成一條試探性的初始中弧線m(w)(w可以看作型線上一點在弦長上的投影),取內接圓的半徑r(w)為中弧線上一點m(w)到上下兩條型線最近點距離的平均值。每根型線q(t)離散為N個點。型線q(t)上一點q的法線矢量表示為n,該法線與初始中弧線交于m(w)。點q到m(w)的距離與r(w)之差為:dq,m(w)=[q-m(w)]gn-|r(w)|。
然后攝動修改初始中弧線m(w)及內接圓半徑r(w)使得dq,m(w)最小,此時點m(w)是內切圓圓心,r(w)是內切圓半徑。這樣逐點得到中弧線及內切圓系列。
這個方法在葉片的前緣及尾緣區有可能碰到這樣的問題:因為初始中弧線m(w)并不是真正的中弧線,前緣及尾緣處型線的法線不一定能和初始中弧線端點相交,迭代計算不一定能開始進行。
綜上所述,必須尋找一種求前緣和尾緣內切圓的辦法。
前緣擬合圓如圖3所示。
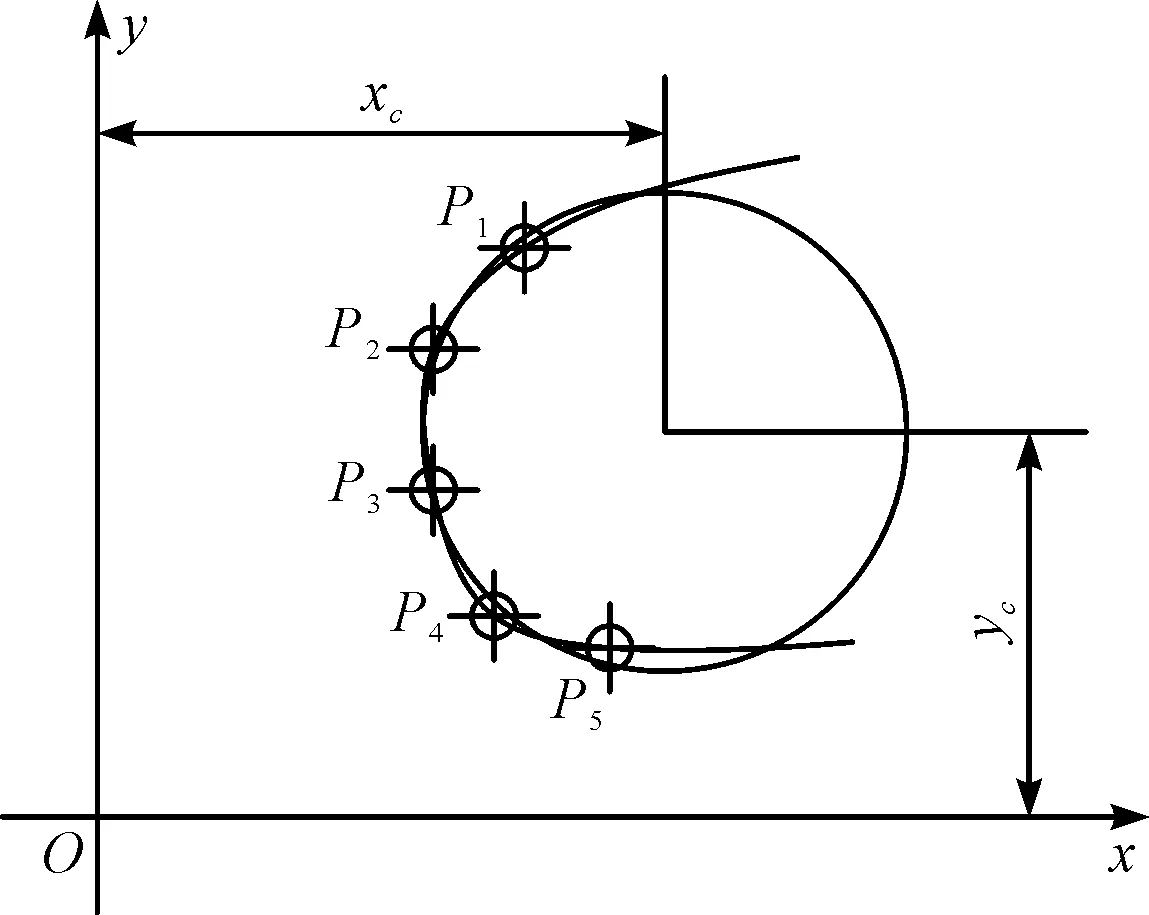
圖3 前緣擬合圓
一般葉片的前緣和尾緣處各有一段型線和中弧線內切圓系列中的第一個圓和最后一個圓是重合的,但這只是在數值上近似重合的。
這個特點用用下式描述:
(xi-xc)2+(yi-yc)2-R2=0,
(1)
式中:xi,yi—前緣或尾緣型線上點i的坐標;xc,yc—中弧線內切圓系列中的和前緣或者尾緣重合的圓心坐標(在下文表示要擬合圓的圓心坐標)。
如果點i不在此圓上,則有下式:
|(xi-xc)2+(yi-yc)2-R2|>0
(2)
上式可以看做是點i相對于要擬合圓的偏離量。利用上式,對于前緣或者尾緣上的n個點可以定義一個函數來表示這些點相對于要擬合圓偏離量總和:
(3)
從圖3可以直觀地看出:當Δ小于某一個非常小的數值時,可以認為擬合成功。如果令這個函數為目標函數,可以把這曲線擬合問題變成一個最優化問題:
(4)
式中:η1—上式中的xc;η2—上式中的yc;η3—上式中的R。
如此處理后就可以利用各種最優化數值方法求解該問題[6-10],得到了xc、yc、R的最優解,也就得到了擬合圓。還可以改變參與擬合點的位置和數量,反復求解問題,通過比較殘差Δ,確定參與擬合前后緣型線部分及擬合圓的最終參數。最后得到構成中弧線的內切圓序列的第一個和最后一個圓。
葉片其余部分的內切圓可以采用前述傳統方法求解。
2 算例及結果分析
本研究試算了NACA65系列葉型中的NACA65(10)-10葉型的中弧線及厚度分布[11]。NACA65(10)-10葉型是NACA65系列葉型的基準葉型。首先利用NACA456軟件在理論中弧線及厚度分布數據的基礎上生成葉型型線的坐標數據[12],然后利用本研究提出的算法從NACA65(10)-10葉型型線的坐標數據反向求得中弧線及厚度分布數據。
該數據和理論數據的比較如圖4所示。

圖4 NACA65(10)-10計算誤差
從圖4可以看到:在前緣(x/l→0)及尾緣處(x/l→1)相對誤差最大達到0.003 5,在型線中部最小,約在10-6數量級。整體上看誤差處于可以接受的范圍。
本研究試算了某型燃氣輪機一系列壓縮機及透平部分的葉型的中弧線。其中,透平部分有些葉型的中弧線最為難算的。這是因為這些葉型曲線部分近乎垂直于x軸,對于插值計算很不利的,特別是前尾緣處用前述傳統方法很容易發散。
本研究首先計算出了和前緣尾緣部分接近重合的圓,如圖5所示。
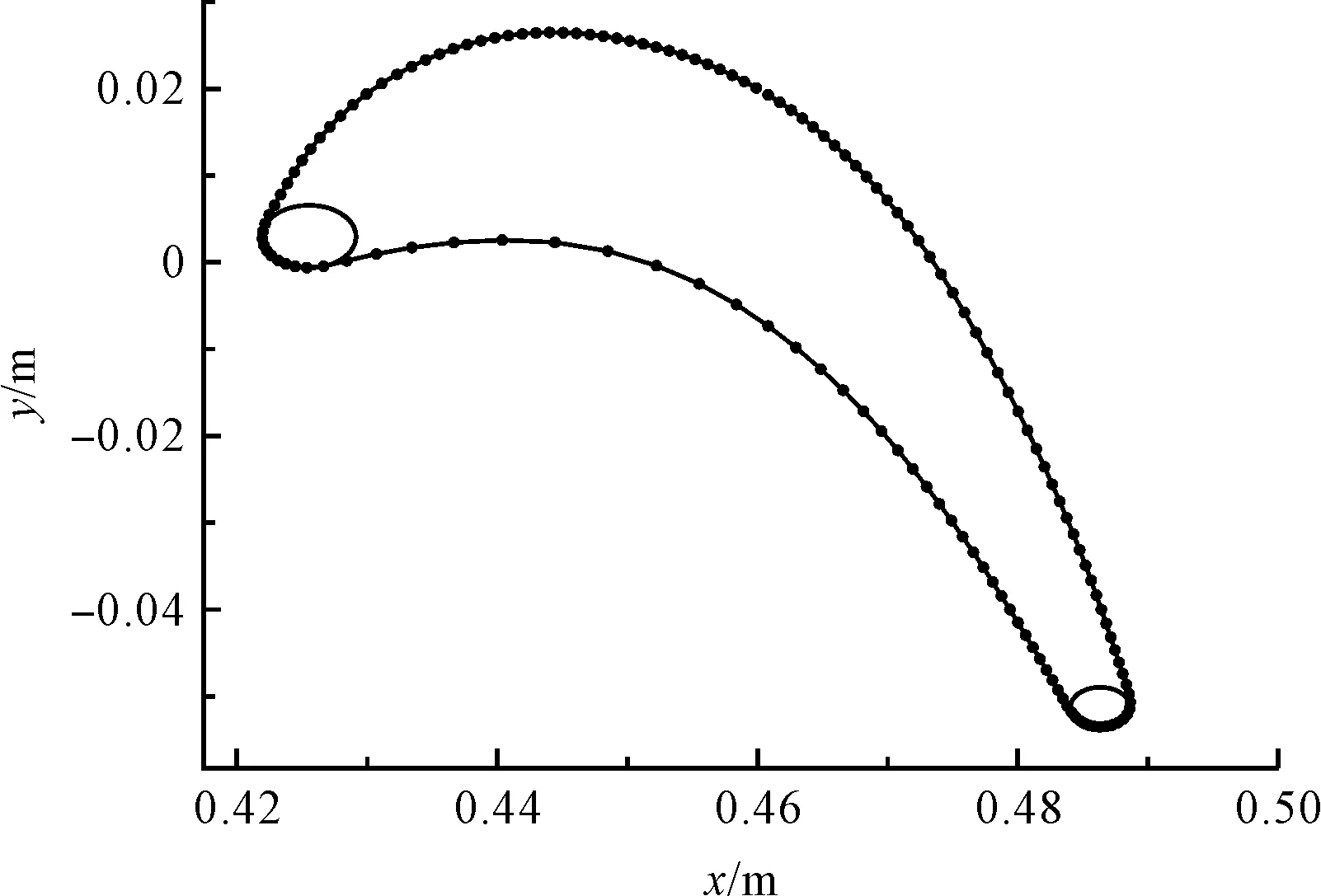
圖5 某型透平葉片截面型線
然后計算除前尾緣其他部分的內切圓序列,如圖6所示。

圖6 某型透平葉片截面內切圓序列
由此可知:這一系列圓和葉片型線相切很好,所以可認為其圓心序列構成了中弧線,其直徑序列構成了葉片厚度分布。
在試算中發現:如果整個葉型只用前述其中一種方法,在葉型前緣壓力面起點處就會計算就會發散,得不到結果。圖6中除了前緣和尾緣處(第一個和最后一個)兩個圓用最優化方法求出,其它的圓都是用傳統方法1或2求出的。這樣就可以完整地求出整個中弧線內切圓系列。
3 結束語
通過對經典NACA65系列葉型及某型燃氣輪機的壓縮機和透平所有葉片的型線進行計算分析驗證,本研究提出了一種在傳統方法基礎上的混合算法,可以比較穩定地求出前尾緣處的內切圓,即前尾緣處內切圓計算方法借助于成熟的最優化計算軟件包實現,其他部分使用傳統方法。
在接下來的研究中,在此基礎上還可以作進一步的改進:首先在型線不同點處,根據該點切線處的斜率旋轉整個型線,使切線不致于垂直于橫坐標軸,提高算法的收斂性;其次利用模式識別方法對于求出的中弧線及厚度分布規律做進一步的識別,判定是否是某種經典葉型的中弧線及厚度分布規律。

