學會轉化 激活思維 解決問題

陳美嬌

【摘要】在小學數(shù)學教學中，數(shù)學知識本身非常重要，但真正對學生以后的學習、生活和工作起長期作用，并使其終身受益的是數(shù)學思想方法。轉化思想是數(shù)學思想的核心，是解決數(shù)學問題的一個重要思想。在教學中，始終緊扣“轉化”這根弦，對提高學生的思維能力、分析問題和解決問題的能力是十分有效的。教師應把隱含在知識中的轉化思想加以揭示和滲透，使他們能用轉化的思想去學習新知識，分析并解決問題，讓學生明確轉化思想的作用，體會運用轉化思想的樂趣，提高學生的數(shù)學素養(yǎng)。

【關鍵詞】轉化思想；激活；思維；解決問題

轉化思想是數(shù)學中最普遍使用的一種思想方法，既是一般化的數(shù)學思想方法，也是攻克各種復雜問題的法寶之一。在小學階段，學生經常面對新知識、新問題，需要從已有的知識和經驗出發(fā)，采用恰當?shù)霓D化手段把陌生問題轉化為熟悉的問題，把復雜的問題轉化為簡單的問題，把未知轉化為已知……在轉化的過程中，學生通過學習嘗試不同的轉化方法，體會、領悟轉化思想的本質，將帶給學生成功的體驗，這是助推思維迅猛飛躍的用不完的燃料。因此，如何在不同的數(shù)學內容教學中挖掘轉化思想，適時向學生有機滲透，使學生通過提煉、總結、理解、應用等循環(huán)反復的過程中逐步感悟出數(shù)學知識、技能中蘊涵的轉化思想，激活思維，是我們數(shù)學老師的一項重要任務。

一、縱向轉化，化新為舊，解決問題

縱向轉化，就是把面臨的新問題轉化為已經解決了的舊問題來處理，通過解決轉化后的舊問題來解決新問題，這是轉化思想中最常用的方法。例如：在探究《平行四邊形的面積》時，我就適時引導學生進行縱向化歸，提出問題讓學生思考：我們學過哪些圖形的面積計算公式？能不能將要學習的平行四邊形的面積轉化為已學過的哪個圖形的面積來學習？學生很快就聯(lián)想到了長方形。接著，我再讓學生小組合作，動手操作，當學生通過“切割”“拼補”等方法將平行四邊形轉化成長方形后，我再引導學生觀察發(fā)現(xiàn)：拼成的長方形跟原來的平行四邊形有什么聯(lián)系？從而推導出平行四邊形面積的計算公式是：平行四邊形的面積=底×高。最后，我再與學生達成共識：把不知道怎樣求面積的圖形轉化為我們會求面積的圖形，就是“轉化”，轉化是解決問題中常用的一種方法，將新問題轉化為舊問題，就是化未知為已知，剛剛通過轉化，我們將要學習的平行四邊形轉化成已學過的長方形，從而獲得了新問題的解決方法。整個過程學生自己動手操作，自主探究，轉化思想就深深嵌入學生的心中，試想，有了這節(jié)課做基礎，后面再學習三角形、梯形和圓面積的計算公式時，學生就能對轉化的思想方法運用自如了。

二、橫向轉化，化繁為簡，解決問題

橫向轉化，就是把復雜、困難的問題轉化為熟悉、簡單的問題來處理，通過化繁為簡的方法解決問題。有些數(shù)學問題比較復雜，學生剛看到題目時不一定馬上就能發(fā)現(xiàn)其中的數(shù)量關系，這時就需要用一些方法將隱蔽的關系明了，使復雜的問題簡單化。轉化方法可以幫助學生使復雜問題簡單化，從而更加清晰地發(fā)現(xiàn)問題、解決問題。數(shù)學問題解決過程中的轉化，其形式多種多樣，由一個問題轉化為另一個問題，由復雜的問題轉化為簡單的問題，但總的轉化路徑是化繁為簡、化難為易、化未知為已知。在教學中應突出轉化思想在解題中的指導作用，注重轉化思想的應用，使學生體悟數(shù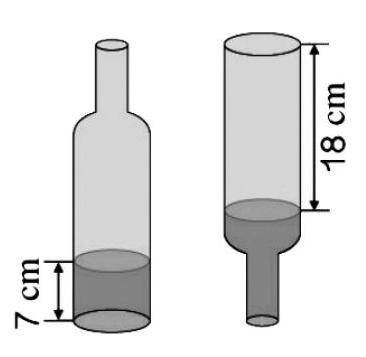)學思想。

例如“一個內直徑是8cm的瓶子里，水的高度是7cm，把瓶蓋擰緊倒置放平，無水部分是圓柱形，高度是18cm。這個瓶子的容積是多少？”教材呈現(xiàn)了一個裝了小半瓶水的礦泉水瓶，下部是圓柱形，而上部是一個不規(guī)則立體圖形。給出了瓶子平置時水的高度和倒置時無水部分的高度，要求這個瓶子的容積。這樣的問題對于小學生來說很難直接解決，教師必須啟發(fā)學生通過觀察瓶子圖，發(fā)現(xiàn)瓶子里的水倒置后，體積不變，水的體積加上18 cm高的圓柱的體積就是瓶子的容積。也就是把瓶子的容積轉化為兩個圓柱的體積，再引導學生列出算式：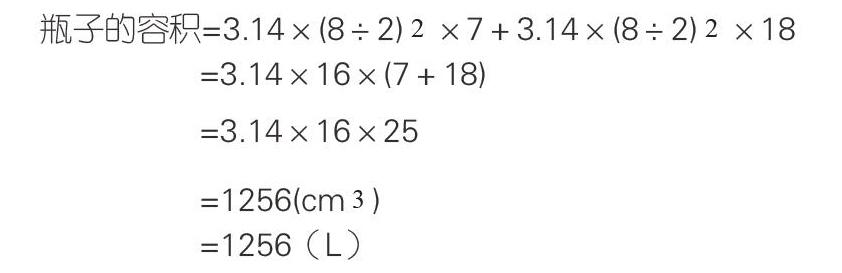

這樣利用了體積不變的特性，把不規(guī)則的圖形轉化成規(guī)則圖形來計算，化繁為簡，清晰有序，使學生對轉化的數(shù)學策略有更為深刻的理解和掌握。

三、同向轉化，分解問題，解決問題

同向轉化，就是把新問題轉化為某一個或幾個簡潔處理的子問題，通過解決子問題，從而解決了新問題。修訂后的人教版《義務教育教科書·數(shù)學》在編排時，注重學生綜合運用知識能力的培養(yǎng)，每一冊教材都出現(xiàn)一些綜合性比較強的題目。知識是一點一滴的積累起來的，學生對于簡單的問題能夠從容處理，而對于多個知識點組成的復雜問題就一籌莫展、束手無策了。因此，遇到復雜的極易混淆的綜合性問題時，教學時教師必須加強滲透數(shù)學教學中重要而又比較常用的一種教學策略，即“化整為零”，把綜合性強的知識細化，逐一擊破。如：“小明家住在電影院的正西650m，小冬家住在電影院的正東700m。周末兩人約好去看下午3時放映的電影。兩人下午2：45同時從家里出發(fā)走向電影院，小明每分鐘步行70m，小冬每分鐘步行65m，2：55兩人能在電影院相遇嗎？如果小明先到電影院后不停留繼續(xù)向東走，從出發(fā)到兩人相遇用了多長時間？相遇地點距離電影院有多遠？”這道題的綜合性較強，涉及方位、時間、速度和路程的數(shù)量關系等知識。教材所提的3個問題可以分別轉化成容易理解的數(shù)學問題。第一個問題“2：55兩人能在電影院相遇嗎？”可以轉化成“10分鐘后兩人是否都能到達電影院？”第2、3個問題是相遇問題中兩個相關問題，可以借助下面的線段圖幫助理解。

解答第2個問題時引導學生理解：“由于小冬家距離電影院更遠，且速度更慢，則他所需要時間更長，如果他能按時到達，那么小明也可以。”接著引導學生根據(jù)：路程和÷速度和=相遇時間，列算式：（650+700）÷（70+65）=1350÷135=10（分鐘）。再解答第3個問題時就比較容易，列式為10×70-650=50（m）。這樣，把綜合性較強的題目化為零碎的小問題，逐一轉化，使知識點更易講透，學生更容易更牢固地掌握知識。

四、逆向轉化，換位思考，解決問題

逆向轉化，就是當按照習慣的思維途徑進行思考出現(xiàn)較難或較繁的情形時，從問題的另一面入手進行思考，從而解決問題。例如：設法求出下面兩種物體的體積。

問題一出，同學A就說：將橡皮泥捏壓成規(guī)則的長方體或正方體形狀，再測量有關數(shù)據(jù)，就能求出它的體積。同學B就反問：那梨呢？梨是不能改變形狀的。同學C：可是梨也沒辦法測量出有關數(shù)據(jù)啊？同學D：……當學生吵得正熱烈，也沒見得有好辦法時，我就適時引導學生進行逆向化歸，讓學生思考：能不能借用我們前面認識的量杯或量筒來解決問題？再出示實驗材料：量杯、馬鈴薯、水、記錄單。請一組同學上臺合作，進行實驗。通過這組同學的實驗，終于得出梨的體積是250立方米。我再引導學生歸納：這種求梨體積的方法就是“排水法”，適合求不規(guī)則物體的體積，用“排水法”求梨的體積，要注意記錄數(shù)據(jù)和將梨完全浸沒到水中。接著我再演示一次實驗過程：先在量杯中倒入一定體積的水，讀出并記錄水的體積是200立方米；再將梨完全浸沒在水中，讀出并記錄水和梨的體積是450立方米；最后計算出梨的體積：450-200=250（立方米）。小結時，我再告訴學生：因為梨無法轉化成我們學過的某個立體圖形，所以我們再用以前學習的立體圖形的體積計算公式就計算不了梨的體積，這時，我們就得轉化思路，換位思考，從問題的另一面入手思考，只有這樣，才能找到解決問題的方法，正所謂“山窮水盡疑無路，柳暗花明又一村”。

實踐證明，在課堂教學中教師如果能夠以教材為媒介，堅持滲透轉化思想，久而久之，學生就會將轉化思想銘刻于心，運用自如，從而大大提高他們解決問題的能力。林碧珍老師將教學分為“三重境界”，分別是授人以“魚”、授人以“漁”和“悟其漁識”。數(shù)學思想方法多達十幾種，如果我們每位老師在課堂教學中都能加以滲透，那么這些思想方法就會慢慢轉化為學生自身解決問題的方法，從而達到“悟其漁識”、“不教而教”的境界。