對高中數學落實“雙基”教學的思考

☉江蘇省海門市四甲中學 王豐波

近年來的很多高考試題都在立足“雙基”的基礎上進行了由易到難的梯度設計與分步設問，入手相對容易的試題對于考生“雙基”的考查意向更加明顯.因此，高中數學教學在數學知識體系與應用基礎知識、方法解決問題的基本技能與能力上也應該傾注更多的關注.

一、數學“雙基”的新內涵

數學基本知識與基本技能是培養學生數學能力、心理品質的載體，學生繼續學習數學并獲得數學能力的發展都必須擁有扎實的數學基本知識與基本技能，不僅如此，其他知識的學習，以及其他能力的形成也都必須在具備“雙基”的基礎上進行.由此可見，“雙基”的教學在學生綜合能力的發展過程中是至關重要的.事實上，很多學生在實際的數學學習中并不重視基礎知識的學習和基本技能的訓練，這樣的意識在導致其他知識學習與技能難以形成的同時也制約了學生能力的提升.不過，值得教師注意的是，“雙基”教學應與能力培養相輔相成，否則，“雙基”教學的效果是難以顯現的.應試教育之下的題海戰、重復大量訓練、炒“夾生飯”、放棄后進生等教學行為極大地造成了“雙基”的異化.

當前人們對數學的認識和需求因為計算機的廣泛使用和信息技術的傳播也產生了巨大的改變，新時期的“雙基”教學也因此被賦予了新的內涵.“雙基”教學的行列中因此加入了培養學生數學應用意識與建模能力的教學任務，不僅如此，這一教學任務應該得到教師的重點關注.同時，與日常生活緊密聯系的算法、概率統計等數學內容也被納入數學課程“基礎”的范疇.簡單說來，現代技術在數學學習中的運用已經成為“雙基”的重要組成部分.

二、數學“雙基”教學的誤區

第一，很多教師在實際教學中更加側重知識、結果及教師的主導等環節，對于學生能力的培養、解題過程的關注及學習的主體地位則是比較容易被忽視的.重視教師“教”而輕視學生“學”的教學行為使得學生學習的意識形態產生了偏離；重視書本教學而輕視生活中數學的教學行為使學生的發現創造意識與能力無法得到激發和培養.很多教師在實際教學中將練習僅僅當作學生知識掌握的衡量工具，對于學生的知識認知過程卻不甚關注，大量重復性的強化訓練往往使學生在解題中更加“機械化”和“自動化”，很多學生在長期的重復練習中形成了不求甚解的消極心理與習慣，學生解題中的遷移能力無法得到應有的鍛煉和培養，一旦問題情境產生變化，學生在解題中不能機械套用解題方法時，也就停滯不前了.

第二，素質教育的口號雖然已為大家所熟知，但考試分數仍然是廣大教師與家長分外重視的“命根子”，因此，很多教師在實際教學中會根據考試要求對教學內容進行取舍與側重，很多不考試的內容也會刪除不教；很多教師在實際教學中對于知識、技能之間的整合也沒有關注，數學思想滲透不到位的情況也使得知識與技能的教學比較支離破碎；很多功利心太強的教師會將知識的發生與發展過程置之腦后，一味壓縮本應該屬于學生的思考時間與空間；也有很多教師為了考試復習的時間能更多一些就會在平時教學中搶進度，很多學生往往在知識掌握的半生不熟之時又面臨新的知識，很多學生在知識與技能的提高上也就失去了應有的前提和基礎.

第三，很多教師在實際教學中信奉“以題為綱”的教學策略，日常練習及各類復習中往往都是系列題、目標題或者成套的模擬題等，很多學校在高三數學后面兩輪復習中往往會讓學生大量練習全國各地的高考試題，深陷“題海”的高中學生更加難以發現數學學習的生動與活潑，數學學習對于這部分學生來說自是毫無興趣可言.

三、“雙基”教學的建議

1.以發展的觀點看待“雙基”

“雙基”的內涵會因為社會進步與數學自身發展而變得更加豐富與深刻.教師在實際教學中應強調“雙基”的形成過程以幫助學生更好地了解概念、結論所產生的背景及其應用.解題教學中應引導學生關注題目的結構形式并進行步步為營的分析與討論.

例1 已知數列{an}與{bn}的各項均為正數且滿足

分析：此題的解決需要注意以下四個關鍵：

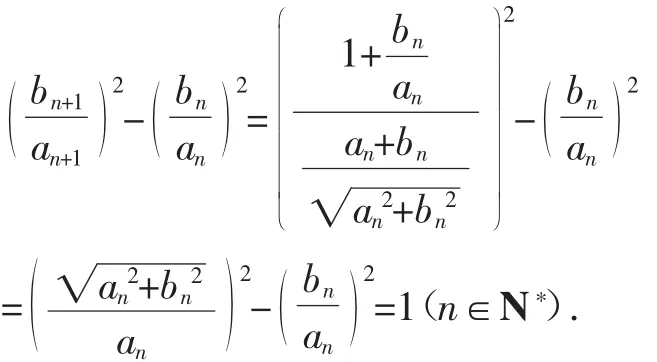
第三，因為等比數列{an}各項均為正數，根據1＜an+1≤可猜想{an}是常數列.設其公比為q，則q＞0.當q＞1時，由an＞0，數列{an}為單調遞增數列，因此必有自然數n，使an+1＞，因此不可能有q＞1；當0＜q＜1時，an＞0，因為數列{an}為單調遞減數列，則一定有自然數n，使得an+1＜1，因此不可能存在0＜q＜1，則q=1，an=a（1n∈N*）.

第四，由反證法可得b1.由b3中至少有兩項相同，與b1＜b2＜b3相矛盾.因此有a1=

2.關注基本方法

近年來的高考試題對于一些解題基本方法的考查還是有所側重的，因此，教師在解題教學中應遵循高考命題選拔性的原則以加強學生解題能力的訓練并發展其思維空間.

例2 已知等差數列{an}的前n項和為Sn，{bn}為等比數列，且a1=b1=2，a4+b4=27，S4-b4=10.

（1）求數列{an}，{bn}的通項公式；

（2）記Tn=anb1+an-1b2+…+a1bn，n∈N*，證明：Tn+12=-2an+10bn（n∈N*）.

分析：（1）根據題中條件易得an=3n-1，bn=2n.（2）關鍵在于求和方法的合理選擇.由（1）有Tn=2an+22an-1+23an-2+…+2na1，① 注意到數列通項由等差數列與等比數列的乘積組成，因此考慮錯位相減來求得數列前n項的和.可得Tn=10×2n-6n-10，而-2an+10bn-12=10×2n-6n-10，故Tn+12=-2an+10bn（n∈N*）.

3.處理好“雙基”與創新的關系

僅僅重視基礎的數學教育也是走不遠的，科學數學教育理論強調“基礎”與“創新”的齊頭并進.“基礎”與“創新”缺少任何一個都無法使數學學習的生命力得到綻放和展現.因此，教師在實際教學中應堅持以學生發展為本并將“雙基”和“創新”放在一起研究，平衡好兩者之間的關系及兩者在教學中的比重，使注重“雙基”與“創新”的教學能夠在科學、合理的設計與落實中都獲得更好的發展，使學生在數學學習過程中展現個性與創新能力并獲得符合學生實際“數學新雙基”的創新與發展.

4.突出能力培養

數學“雙基”水平綜合發展往往會在學生的數學綜合能力上體現出來，數學教學包含發展學生能力這一重要的教育目標，因此，教師在實際教學中應幫助學生牢固掌握基礎知識與基本技能，關注知識點之間的關聯、解題技能的變式進行教學，使學生能夠在重視“雙基”但突出能力培養的合理化教學中形成整體性的知識網絡并獲得能力的發展，學生在各種不同情境中靈活運用已學知識與技能正是其數學能力的最佳體現，數學教學中的變式教學正是基于這一目標而產生的.

數學這門基礎學科在解決實際問題、日常生活、其他學科學習中都會產生巨大的作用，高中數學教師應關注數學與其他學科、生活實際之間的聯系，著眼于學生數學應用意識的形成與發展，立足“雙基”進行科學的數學教育以促成學生數學能力、情感、態度、價值觀的長足發展.F