利用數學實驗研究同底指數函數和對數函數的圖像位置關系

☉湖北省武漢中學 劉志江☉湖北大學附屬中學 李 俊

在教學中適度有效地開展數學實驗，不僅能使學生掌握必要的數學知識，更重要的是有助于提高他們的積極性，培養他們樂于思考探索的品質，有利于提高他們動手操作及分析問題、解決問題的能力，是一種在新課程教學中值得借鑒的教學方法.以下介紹一次開展數學實驗的教學過程.

在學習對數函數時，類比同底的指數函數，根據對數函數的圖像得到對數函數的性質是教學中的一個重要環節，筆者用卡西歐fx-CG20圖形計算器開展數學實驗，讓學生動手、用心、入腦，并起到了事半功倍的效果.

我們的學生接觸圖形計算器時間不長，但同學們對新生事物天生有強烈的好奇心，在實驗的開始，在他們不斷摸索操作圖形計算器時，我給出了一些參考操作步驟，以下簡述操作過程（文字說明后的括號內是相應的順序按鈕操作）.

1.開機（ AC/ON ）.

2.切換到動態函數模式（ MENU6）（圖1）.

3.輸入函數y=A（x?ALPHA x，θ，T∧x，θ，T EXE）（圖2?）.?

圖1

圖2

圖3

圖4

5.設置變量A的初始值為0.1（ F40 1EXE）（圖4）.

6.設置變量A的開始值為0.1（ F20 1EXE）.

7.設置變量A的終止值為1.9（ 1 9EXE）.

8.設置變量A的變化步長為0.2（ 0 2EXE）（圖5）.

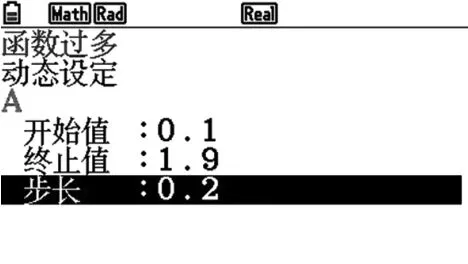
圖5

圖6

9.返回到上一頁面（ EXIT）.

10.設定動態速度為單步執行（ F3 F1）（圖6）.

11.返回到上一頁面并進入查看窗設置頁面（EXIT SHIFT F3 ）（圖7）.

圖7

圖8

12.設定查看窗為初始窗并返回到上一頁面（F1 EXIT）.

13.進入動態圖模式（ F6）.

14.改變A的值，顯示函數y=Ax與y=logAx的動態圖（?或?）（圖8）.

同學們對圖形計算器的功能和作用產生了濃厚的興趣，部分同學通過研究后建議在上述圖中一并作出y=x的圖像，這樣可以更好地體現互為反函數的圖像對稱性，于是有了如下的圖像（圖9）.

圖9

圖10

通過變化A的值，感受A的變化對圖像的影響（圖11）.

圖11

由此，同學們從動態圖中得到了同底指數函數與對數函數的相關性質：定義域、值域、單調性等，甚至不同底的對數函數在區間（0，1）和（1，+∞）上的比較也一目了然.可見，圖形計算器作為輔助教學工具在教學中起到了非常好的效果，同學們在探究過程中對圖形計算器的操作也相當熟練了.

讓人驚喜的是，居然有同學提出關于同底指數函數與對數函數圖像的交點個數問題，實現了“問題從學生中來，到學生中去”的良性循環.

在了解了圖形計算器的操作基礎上，絕大部分同學得到了y=Ax與y=logAx圖像交點個數的結論：

1.當A大于某一介于1.4和1.5之間的數（以下記這個數為M）時，兩函數圖像沒有交點（圖12、13）；

圖12

圖13

2.當A等于M時，兩函數圖像有一個交點（圖14、15）；

圖14

圖15

3.當A在（1，M）上變化時，兩函數圖像有兩個交點（圖16、17）；

圖16

圖17

4.當在（0，1）上變化時，兩函數圖像有一個交點（圖18）.

圖18

但上面結論4是錯誤的，很多同學表示不相信，問題在哪兒呢？經過研究，有同學把圖像放大了，有如下四個圖（圖19、20、21、22）.

圖19

圖20

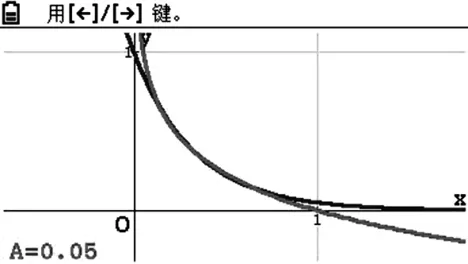
圖21

圖22

看來有一個數N介于0.05和0.08之間，有：

（1）當A在［N，1）上變化時，兩函數圖像有一個交點；

（2）當A在（0，N）上變化時，兩函數圖像有三個交點；

所以，同底指數函數與對數函數圖像的交點個數情況如下：

1.當A＞M時，兩函數圖像沒有交點；

2.當A=M時，兩函數圖像有一個交點；

3.當A∈（1，M）時，兩函數圖像有兩個交點；

4.當A∈［N，1）時，兩函數圖像有一個交點；

5.當A∈（0，N）上變化時，兩函數圖像有三個交點.

至此，同底指數函數與對數函數圖像的交點個數情況分類討論看似已結束，可是又有同學提出，上面的M和N這兩個數到底是多少？看來，問題如抽絲剝繭，被層層遞進，這樣就把函數另一相關知識點——“導數”被提出來了，同學們熱切期待著對這個相關知識點的探索與學習.

可見，通過圖形計算器這個實驗平臺，讓學生們自己動手一起探索，促進了師生之間的交流合作，在探索過程中，教師有意識地將數學研究的思想方法滲透到教學過程中，學生思維活躍，研究容量大，圖形計算器的結合使用既提高了課堂效率，也豐富了學生對數學研究的方法.在他們動手操作的同時，激發了他們的創造性思維，充分體現了數學實驗有利于培養學生的數學動手能力、表達能力、觀察能力和創新能力.

注：由導數相關知識推理，上述M和N這兩個數分別如下：