城市軌道交通網絡的優化模型
王國宇 張嘉琪 張永利 丁明明 呂文英 紀楠
摘 要:本文以城市軌道交通網絡建設問題為研究對象,將交通線路合理性和可達性作為限制條件,建立交通網絡的多目標優化模型。此模型以總出行時間最少、線路總長度最小以及總換乘次數最少為目標建立多目標函數,并對模型進行求解。該模型可對可能的軌道交通線路進行篩選,得到最優的線路網絡布局。
關鍵詞:城市軌道交通 優化模型 多目標函數
中圖分類號:U239.5 文獻標識碼:A 文章編號:1672-3791(2018)03(b)-0023-02
隨著科技的進步,城市軌道交通在公共交通中的重要性越來越高。20世紀至今,國內城市紛紛開展軌道交通的研究,取得了不錯的研究成果。本文通過分析軌道交通的特點,構建模型優化軌道交通的線路布局。
1 模型建立
1.1 模型目標及限制條件
1.1.1 模型目標。
目標Ⅰ:總軌道交通出行時間最少,即
式(1)中,為地區和之間的客流;為在其路徑上所需時間。
目標Ⅱ:總的軌道交通線路長度最小,即
式(2)中:為交通線路;為二進制變量;1代表選擇線路,0則不選。
目標Ⅲ:總換乘次數最少,即
式中:為總的換乘次數。
本文采取線性加權方法求解多目標規劃模型,此目標函數則為:
其中:為線路總長度的權重;為總換乘次數的權重。
1.1.2 限制條件
將軌道交通的線路合理性和可達性考作為限制條件。
(1)軌道交通線路合理性。
其中:和分別為線路總長度最小值和最大值。
(2)任意兩主要交通區域之間可達性:
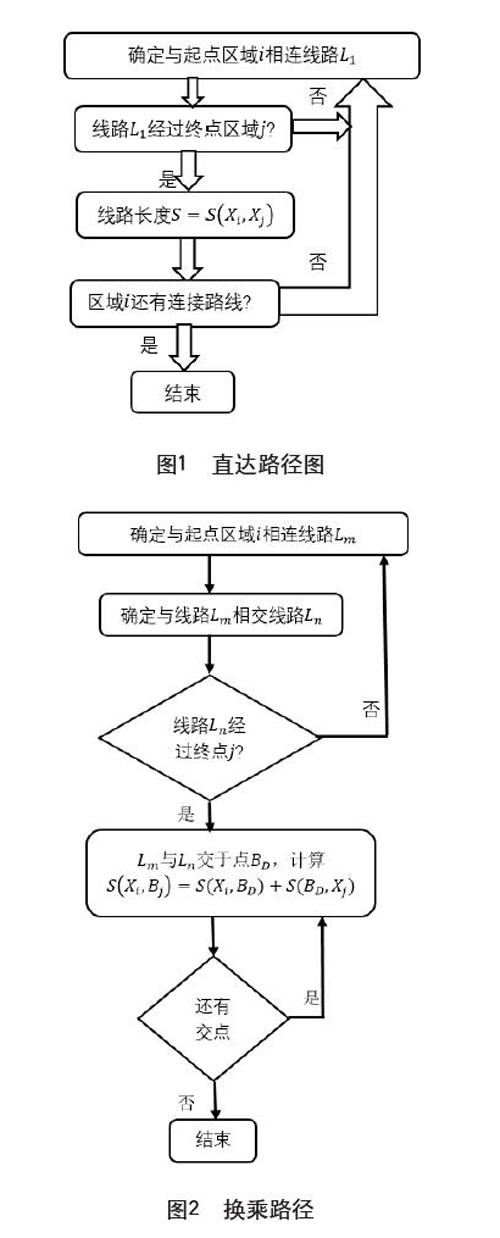
1.2 路徑
(1)直達路徑如圖1所示。
(2)換乘路徑如圖2所示。
2 模型求解
對此模型選取遺傳算法求解。
2.1 編碼與解碼
采用0-1編碼,假設備選軌道線路有條,代碼依次為,染色體長度為。用“1”表示選擇該線路,”0“表示不選該線路。
2.2 適應度函數
令為適應度函數。為第個個體的適應度,為目標函數最大值,為第個個體目標函數值。
2.3 限制條件處理
從群體中挑選兩個個體,按以下規則進行比較。
(1)兩個體均為可行解,適應度更大的更大概率進入下一代。
(2)兩個體為一可行解和不可行解,可行解更大概率進入下一代。
(3)兩個體均為不可行解,更接近最大適應度值的更大概率進入下一代。
2.4 遺傳算法流程
(1)初始化種群數目、染色體長度、迭代總代數、交叉概率和變異概率。
(2)隨機產生初始種群,迭代次數設為1。
(3)得出各個個體對應的解,代入模型中得到對應的路徑二進制碼,解碼后再計算每個個體的適應度。比較個體適應度值,若迭代次數,則輸出適應度值最小個體,否則進入下一步。
(4)使用精英機制,直接選擇前代最優個體。
(5)兩個不同的染色體根據交叉概率按照某種方式交換其部分基因。
(6)基因根據變異概率,進行變異,迭代次數,得到新種群,并轉到第三步。
3 結語
以總出行時間最少、出行線路總長度最小及總換乘次數最少為優化目標,將交通線路合理性和可達性做為限制條件,建立了城市軌道交通網絡優化模型。該模型為多目標優化函數,為城市軌道交通網絡的優化提供了理論建議。
參考文獻
[1] 胡汪源.基于時空網絡的城市軌道交通乘務排班優化模型與算法[D].北京交通大學,2017.
[2] 葉青.城市軌道交通網絡脆弱性分析與客流協同控制研究[D].西南交通大學,2016.
[3] 張旻沁.基于拓撲結構的城市軌道交通網絡連通可靠性分析與優化[D].東南大學,2016.
[4] 李麗.基于復雜網絡理論的城市軌道交通網絡可靠性研究[D].北京交通大學,2015.
[5] 呂曉東.城市軌道交通列車運行交路問題研究[D].西南交通大學,2012.

