培養中年級學生思維敏捷性

梁 寒

（南京民辦實驗學校，江蘇 南京）

數學是思維的“體操”，可以鍛煉學生的思維能力，使其不斷地發展。學生處在中年級向高年級過渡時期，思維能力的發展處在轉折時期，抽象概括、分類、比較和推理能力開始慢慢形成。題目量在增加，題目難度也在提高，這也決定了對學生思維敏捷性的要求也在提高。如何才能提高學生的思維敏捷性呢？

一、提高數學運算能力

針對中年級教材內容主要提高學生兩位數乘兩位數、三位數乘兩位數的筆算能力、除數是兩位數的除法計算以及運用運算律進行簡便運算的能力。首先學生應該在理解算理和算法基礎上進行正確計算，結合實際問題感受簡便運算。

①月星小區有16幢樓，平均每幢樓住128戶。月星小區一共住了多少戶？

例如上圖：在教學三位數乘兩位數筆算時，結合學生已有的認知，學生會說可以先計算6棟樓共住了多少戶，然后再算出10棟樓共住了多少戶，最后加起來。經歷這個過程學生就會理解豎式計算的算理，更能深入地理解每一步求出的是什么，真正學透，而不是機械式地計算。這樣舉一反三的能力也會慢慢提高。

再例如學習乘法結合律時：如下圖，

④華豐小學舉行跳繩比賽，規定每個班選派23人參加。每個年級有5個班，6個年級一共要選派多少人參加比賽？

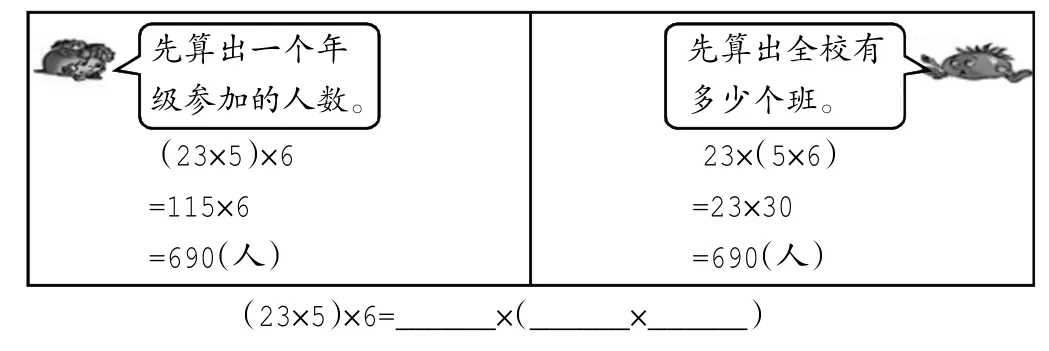
再寫幾組這樣的算式，算一算，比一比，你有什么發現？

如果用字母a、b、c分別表示三個乘數，上面的規律可以寫成：

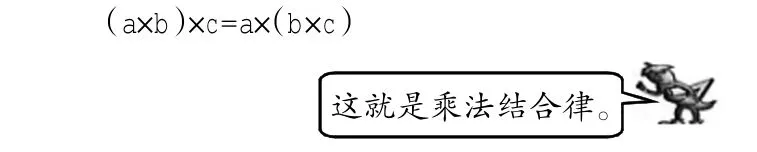
先出示例題，讓學生理解題意，出示問題：要求6個年級一共要選派多少人參加比賽？你是怎么想的，根據以前學過的連乘，學生會想到可以先求出6個年級一共有5×6=30（個）班，然后再根據每班23人就可以求出一共多少人參加比賽，列成綜合算式就是23×（5×6）；同樣也會有學生想到可以先求一個年級有多少人參加，列式是23×5，再乘6就可以求出6個年級一共要選派的人數，列成綜合算式是（23×5）×6，如果順序不同教師可以引導學生稍微調整，因為這樣比較可以看得更清晰。學生通過思考過程會知道兩種算法結果肯定相等，進而會得出乘法結合律。經歷這一系列過程學生就更能理解什么是乘法結合律，這樣在純計算時學生就不是冷冰冰地計算，腦子會想到這一場景，錯誤率就會減少。

還有教學乘法分配律時：如下圖

四、五年級一共有領多少根跳繩？

乘法分配律是個難點，學生掌握得一直不太好，這就要反思在教學例題時有沒有讓大部分學生理解這兩種方法之間的聯系。第一種方法學生可以先算出四五年級一共有10個班，再根據每班領24根跳繩，可以求出一共要領多少根跳繩。第二種方法是把四年級和五年級的跳繩分別求出來，然后把兩個年級跳繩加起來。最后根據兩種方法算出相等得出乘法分配律，這一步應該讓學生多說，點名說，同桌互說。理解清楚兩個數的和乘一個數應該等于這兩個數分別乘一個數再相加。

所以學生的計算能力的培養離不開情境教學，計算能力增強了，學生思維敏捷性也會得到提高。

二、增強空間想象能力

空間想象能力就是學生對客觀事物的空間形式進行觀察、分析和抽象思維的能力。這種數學能力的特點在于善于在頭腦中構成研究對象的空間形狀和簡明的結構，并能將對實物所進行的一些操作在頭腦中進行相應的思考。例如：

③你會把方格紙上的三角形繞點A逆時針旋轉90°嗎？

例3是教學旋轉知識，出示圖片后先讓學生動手旋轉試試，看看用實物旋轉后三角形位置，讓學生通過實際操作先在腦中建立表象，然后慢慢表象加深后學生就要通過空間想象旋轉后的圖形位置，最后動手畫出來。

三、提高解決問題的能力

“問題是數學的心臟”，通過解決問題培養學生自主性、創造性和解決問題的能力，學生平時會出現以下情況：有時，面對數學問題，無從下手；有時，明明思路很清楚，就是解不出來；有時解題到途中，卻是“山窮水盡”。所以在教學中老師要求學生通過認真審題—畫圖—分析數量關系—列式解答—檢驗等步驟來完成。還會通過一些對比練習進行區分理解。

例如在教學相遇問題時，如下圖：

小明和小紅同時從馬路的同一地點出發，同向而行。小明的速度是70米/分，小紅的速度是60米/分，出發4分鐘后兩人相距多少米？

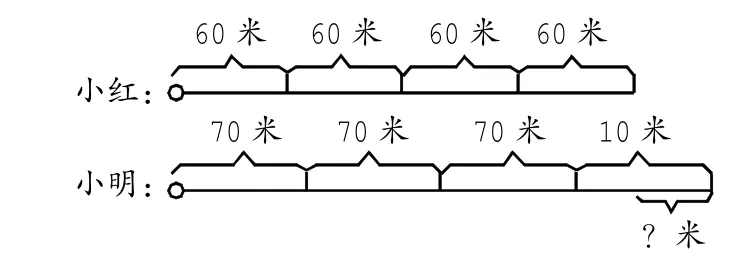
小明和小紅同時從馬路的同一地點出發，相背而行。小明的速度是70米/分，小紅的速度是60米/分，出發4分鐘后兩人相距多少米？

這兩種題型就是和學生做一個對比講解，同一個地點、同時同向行駛時求兩人相距路程是求兩人路程之差。同一地點、同時相背而行時求兩人相距路程是求兩人路程之和。這兩種題型不管是畫圖還是思路上都是有所不同的。

四、加強動手操作能力

動手操作是學生根據教師教學情景的創設，通過動手操作學具來探究數學問題，獲得數學結論，并因此更好地理解數學知識的教學手段。數學是一門抽象的學科，組織學生進行操作活動，促使學生手、腦、眼、口多種感官參與學習，提高感知效果，為學生認識抽象的數學概念打下良好的基礎。四年級下冊第七單元學習了認識三角形、平行四邊形和梯形，在學習中教師注重讓學生通過動手拼一拼、量一量、測一測等活動，讓學生發現知識。

例如在教學三角形內角和是180°時，如下圖：

想辦法把每個三角形的3個內角拼在一起，看看拼成了什么角。

自己再任意畫一個三角形，先剪下來，再拼一拼。

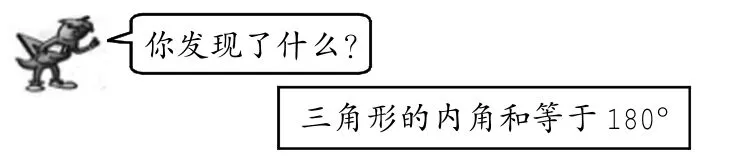
讓學生先動手操作，可以量一量三個角的度數再加起來；可以把三個角撕下來拼一拼；也可以把三個角折在一起。通過學生自己的探索會發現三角形內角和是180°。

基本技能的訓練是數學知識轉化為數學能力與素養的中心環節，它不僅在知識過程中對領會與鞏固知識起促進作用，而且在知識深化形成高層次新知識中起橋梁作用，使學生實踐能力、思維能力、創造能力得到培養，綜合素質得到提高！

強化技能訓練一定要在學生切實理解運算法則、定律、性質等基礎上，要求學生熟記一些常用的數據，平時堅持適量的口算和應用題練習，通過視算、聽算、口答、速算比賽等，采用“定時間比做題數量”“定做題數量比完成時間”的訓練方式，強化學生的基本技能，從而達到培養思維敏捷性的目的。