空間幾何體的截面

張小蓉，張秀蓉

（1.泉州第五中學(xué)，福建 泉州；2.泉州城東中學(xué)，福建 泉州）

高考文科數(shù)學(xué)對(duì)學(xué)生的空間想象能力有較高的要求，近幾年有多地的文科數(shù)學(xué)高考中直接或間接地出現(xiàn)了作圖題，其中如何做出空間幾何體的截面更是重難點(diǎn).

如2015年全國(guó)卷Ⅱ，第19題：

如圖 1，長(zhǎng)方體ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，點(diǎn)E，F(xiàn)分別在A1B1，C1D1上，A1E=D1F=4.過(guò)點(diǎn)E，F(xiàn)的平面 α 與此長(zhǎng)方體的面相交，交線圍成一個(gè)正方形.

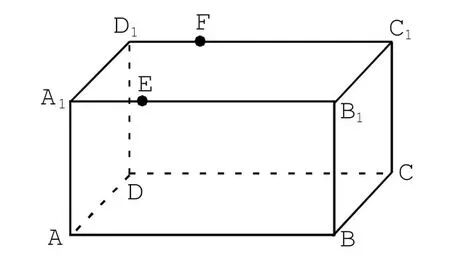
圖1

（1）在圖中畫(huà)出這個(gè)正方形（不必說(shuō)明畫(huà)法和理由）；

（2）求平面α把該長(zhǎng)方體分成的兩部分體積的比值.

那如何作出一個(gè)幾何體的截面？首先，截面的邊界必在幾何體的表面，作截面的本質(zhì)是找出平面與幾何體表面的交線；其次，判斷平面與幾何體的哪些表面有交線，由公理三可知兩個(gè)平面若有一個(gè)交點(diǎn)，必有一條交線；最后，作出交線即可.筆者將作交線分出以下兩種題型：

一、相交型

例1.（2015秋·石景山區(qū)期末）如圖2，有一個(gè)正方體的木塊，E為棱AA1的中點(diǎn).現(xiàn)因?qū)嶋H需要，需要將其沿平面D1EC將木塊鋸開(kāi).請(qǐng)你畫(huà)出平面D1EC截正方體的截面.

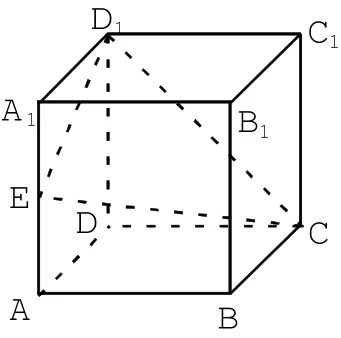
圖2

解法一：1.判斷線段EC并不在正方體表面，點(diǎn)C為平面D1EC與平面ABCD的交點(diǎn)，所以平面D1EC與平面ABCD存在交線；

2.顯然點(diǎn)C對(duì)邊D1E與平面ABCD不平行；

3.在平面A1D1DA內(nèi)，延長(zhǎng)D1E與直線DA相交于點(diǎn)F，則直線CF與直線AB相交于點(diǎn)G，聯(lián)結(jié)EG；

則易得四邊形CGED1為所求截面

二、平行型

同樣我們觀察例1，有解法二：

1.判斷線段EC并不在正方體表面，點(diǎn)E為平面D1EC與平面A1B1BA的交點(diǎn)，所以平面D1EC與平面A1B1BA存在交線；

2.且顯然點(diǎn)E對(duì)邊CD1與平面A1B1BA平行；

3.在平面A1B1BA內(nèi)，過(guò)點(diǎn)E作直線與直線CD1平行，與直線AB交于點(diǎn)G，聯(lián)結(jié)CG；

則易得四邊形CGED1為所求截面.

從例1的解答中，我們可以總結(jié)出，要得出兩平面的交線，只需先找出一個(gè)交點(diǎn)，并判斷該點(diǎn)的對(duì)邊與平面是否平行，并相應(yīng)地作延長(zhǎng)線或平行線即可.

除了題目直接要求作出截面或交線以外，以下兩個(gè)題型也與截面有關(guān)：

例2.如圖3，四棱錐P-ABCD中，點(diǎn)E，F(xiàn)分別為線段CD，PB的中點(diǎn)，在線段PC上是否存在一點(diǎn)Q使得AFQE四點(diǎn)共面，若存在求的值，不存在請(qǐng)說(shuō)明理由.

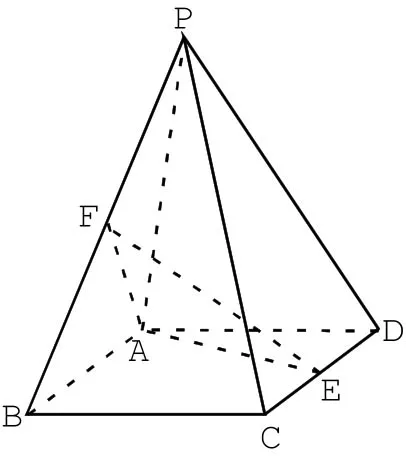
圖3

解題思路：延長(zhǎng)AE交BC于點(diǎn)G，聯(lián)結(jié)FQ交PC于點(diǎn)Q，即所求；

易得點(diǎn)Q是三角形PBG的重心，所以

例3.如圖4，直三棱柱AB悅-A1B1C1的底面為等腰直角三角形，粵月=粵悅；

點(diǎn)閱為線段月悅1的中點(diǎn)，證明：月悅⊥平面粵粵1閱.

解題思路：將三角形AA1D擴(kuò)大至截面，易證.

如例2，例3，立體幾何中很多題目的難點(diǎn)在于如何找出平面相關(guān)的平行和垂直關(guān)系，有時(shí)將圖形擴(kuò)大至截面可使問(wèn)題迎刃而解.

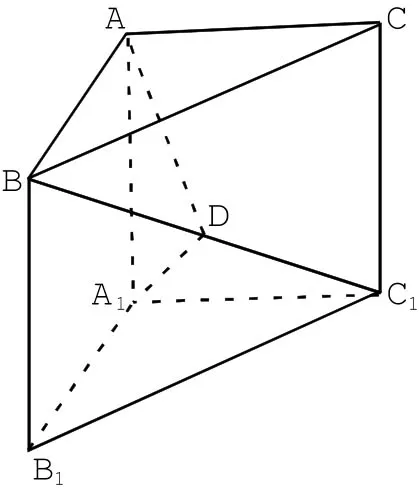
圖4