MATLB軟件在高等數(shù)學課程中的應用研究

熊 慧

（本溪廣播電視大學 遼寧 本溪 117000）

1 引言

近年來，科學技術的快速發(fā)展帶動了社會文明的進步，人們在發(fā)現(xiàn)新的知識的過程中，對于傳統(tǒng)理論知識的學習卻仍未停止。在高等教育規(guī)模不斷擴大的情況下，社會范圍內(nèi)對成人高等教育的各項要求也表現(xiàn)出明顯的提高，高等數(shù)學是普通高校和成人高校學生所接觸的基礎科目之一，在這一科目的學習過程中，除了需要扎實的數(shù)學基礎知識體系以外，還應當具有一定的創(chuàng)造力。基于社會發(fā)展對高校學生要求的提高，在高等數(shù)學課程的設計過程中，則需要對其內(nèi)容與實施方法加以創(chuàng)新，從而實現(xiàn)高等數(shù)學課堂教學質量與效率的提高。其中，MATLAB軟件作為一種普遍使用的應用型軟件，能夠適用于多種類型的基礎課程，它的全稱為“Matrix Laboratory”，也就是所謂的“矩陣實驗室”。由于MATLAB軟件的優(yōu)勢體現(xiàn)在對批量數(shù)據(jù)的處理上，借助大量的專業(yè)工具，實現(xiàn)了MATLAB軟件功能的不斷擴充，甚至可以根據(jù)使用環(huán)境的不同，進行專業(yè)工具的訂制設計。基于MATLA軟件語言的簡便性，便于本科生快速掌握該軟件的使用技巧和方法，這也是該軟件在課程教學中得到廣泛使用的根本原因之一。

2 MATLAB軟件可視化功能在高等數(shù)學課程中的體現(xiàn)

高等數(shù)學繼承了傳統(tǒng)數(shù)學科目的抽象性特點，在高等數(shù)學的學習過程中，為降低學習難度，則可以采取“數(shù)形轉換”的方式，將抽象的問題形象化處理，這里就需要使用到MATLAB軟件的可視化功能。所謂MATLAB軟件的可視化功能，就是利用MATLAB軟件自帶的繪圖工具，將數(shù)學關系中所有點的坐標在空間中進行呈現(xiàn)，也就是繪制圖形的過程。整個過程都是通過MATLAB軟件的程序運算完成的，且圖形繪制后任意一點的坐標值都滿足原函數(shù)的數(shù)學關系。

2.1 直角坐標系函數(shù)的MATLAB表示

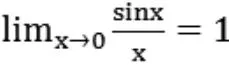
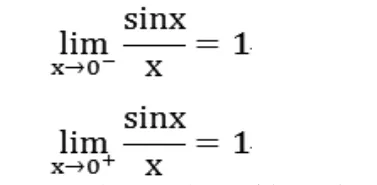
細心的人可以看出，當x從0的兩側無限接近于0的情況下，其最終結果為1，為更好的分析這一結果，我們可以通過設定取值區(qū)間加以深入研究，在這里，取值區(qū)間設定為x∈[-2，2]，x≠0時，則可以借助MATLAB軟件的數(shù)據(jù)分析功能，對固定區(qū)間內(nèi)數(shù)據(jù)進行等分處理，具體程序如下所示：

x=-2：（4/29）：%在現(xiàn)有區(qū)間的基礎上對其進行奇數(shù)等分；

x=sin（x）.（x/29）；%計算當前f（x）的函數(shù)的結果；

plot（x，y，‘o’）；%二維空間描點；

axis equal；%設定二維空間圖像的坐標比值；

grid on；%在二維空間內(nèi)繪制分格線；

xlabel（‘x’）；ylabel（‘y’）；%標記已經(jīng)明確的x，y坐標軸；

title（‘函數(shù)f（x）=sin（x）/x）的圖像’；

經(jīng)過MATLAB軟件的計算之后，則得到如圖1所示的二維圖形：函數(shù)f（x）=sin（x）/x的圖像

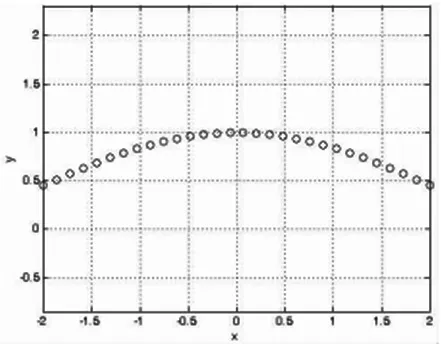
圖1 函數(shù)f（x）=sin（x）/x的圖像

2.2 隱函數(shù)圖像的表示

在高等數(shù)學中，對于無法進行顯化的圖像也就缺乏對應的函數(shù)表達式，則可以通過更加復雜的作圖方式進行求解，利用MATLAB軟件的繪圖工具，得到最終圖形的結果。

以方程ey+xy-e=0為例，通過一系列計算和變換之后，可以得出該方程的隱函數(shù)y=y（x）。為實現(xiàn)對隱函數(shù)中相對點的二維坐標確認，則需要對自變量x的值進行確認，并利用MATLAB軟件中的函數(shù)fsolve得出對應的函數(shù)值y，也就是非線性方程求解的過程。然而，這里需要提醒的是，MATLAB軟件中的fsolve函數(shù)所得到的y值并不是精確值，而是在一定精度范圍內(nèi)的近似值，即便如此，對于以圖形方式表示抽象函數(shù)關系已經(jīng)足夠，其中MATLAB程序編寫如下所示：

x=0：.1：10；%確定橫軸x上的各個點；

f=inline（‘exp（y）+x*y-exp（1）’）；%左函數(shù)的確認

for i=1：length（x）

y（i）=fsolve（@（y）f（x（i），y）…0，ptimset（‘Display’，‘off’））；%利用fsolve函數(shù)求解

end

plot（x，y，‘d’）；%繪制（x，y）圖形

grid on；%繪制分格線

xlabel（‘x’）；ylabel（‘y’）；%為x、y軸做標記

title（‘隱函數(shù)ey+xy-e=0的圖像’）

由于fsolve函數(shù)在實際使用過程中需要一定的運算時間，隨著x軸取點數(shù)量的增加，計算時間也將隨之延長，以上部分代碼所得到的圖像如圖2所示。隱函數(shù)ey+xy-e=0的圖像。

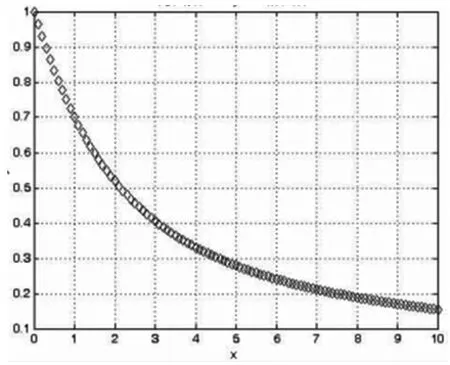
圖2 隱函數(shù)e^y+xy-e=0的圖像

2.3 極坐標解題中函數(shù)圖像的應用

theta=0：（2*pi/100）：2*pi；%從極坐標中取點

rho=1+cos（theta）；

x=rho.*cos（theta）；

y=rho.*sin（theta）；%完成極坐標系向直角坐標系的對應轉化

plot（x，y，‘o’）；%繪制直角坐標系圖像

grid on；%繪制分格線

xlabel（‘x’）；ylabel‘y’；%對應坐標軸的標記

title（‘函數(shù)ρ=1+cosθ的圖像’）

在實際計算過程中，由于極坐標系與直角坐標系之間需要完成多次轉化，因此，整個繪圖過程將持續(xù)一段時間，選點越多，繪制周期也就越長，心形圖的曲線也將更加美觀。圖3為函數(shù)ρ=1+cosθ的圖像。

圖3 函數(shù)ρ=1+cosθ的圖像

3 高等數(shù)學課程中MATLAB軟件的符號運算功能的應用

在MATLAB軟件的各種功能中，符號功能的存在解決了困擾了大多數(shù)學生在復雜導數(shù)、積分、微積分計算問題，通過科學的程序設計，能夠實現(xiàn)對應數(shù)學題目的快速解答，下面以MATLAB軟件的符號運算功能求冪指函數(shù)y=u(x)v（x）的導數(shù)為例進行介紹。

在使用MATLAB軟件冪指函數(shù)y=u(x)v（x）求導過程中，相關程序設計較為簡單，具體如下：

syms x；%設定符號變量

diff（U(x)V(x)）；%求導計算

經(jīng)過MATLAB軟件的求導計算，則可以得出最終個結果為：

由此可見，使用MATLAB軟件后之后，原來較為困難的求導過程也就僅僅是兩行代碼的問題，所以，在高等數(shù)學的學習過程中，學生們應善于使用類似于MATLAB的相關軟件，提高解題效率。

4 結語

高等數(shù)學課程所涉及內(nèi)容較多，且大量數(shù)學計算的存在導致其難度較其它學科明顯增加，為此，將MATLAB軟件融入高等數(shù)學課程之中，能夠實現(xiàn)課程內(nèi)容優(yōu)化，激發(fā)學生在高等數(shù)學學習方面的興趣，實現(xiàn)學生在理論知識水平和實踐水平的共同提高。