選擇梳理 區別利用

丁奎云

【摘 要】新課程理念強調以生為本，強調課堂互動，強調課堂生成。有效利用課堂生成問題，要分析選擇、梳理分類、區別應對，有效利用。提問題，引發思考，讓疑問成為學習的觸發點；議典型，鼓勵創造，讓創造成為教學的生長點；辨是非，強化認知，讓錯誤成為知識的鞏固點；釋歧義，拓展思維，使矛盾成為課堂的延伸點。在學生豐富的生成和教師的積極應對中，有序推進課堂教學，不斷提高課堂效率。

【關鍵詞】課堂；生成；策略

《課程標準》強調：“師生雙方的互動往往會‘生成一些新的教學資源，這就需要老師能夠及時把握，因勢利導，適時調整預案，使教學活動收到更好的效果。”

前蘇聯著名教育家蘇霍姆林斯基說過：“教育的技巧并不在于能預見到課堂的所有細節，而是在于根據當時的具體情況，巧妙的在學生不知不覺中做出相應的變動。”

生成是師生互動的必然。面對豐富的課堂生成，我們要如何應對，才能有效利用，推進課堂教學，促進課堂高效呢？

筆者就自己的一些經驗，與大家做個交流。

一、提問題，引發思考

愛因斯坦曾經說過：“提出一個問題比解決一個問題更重要。”“學起于思，思源于疑。”問，是思維的開端，創新的基礎。

從出示課題到情境呈現，從理解題意到分析關系，從計算到檢驗，從空間想象到操作驗證，學生的疑問貫穿課堂始終。教師要不斷地鼓勵學生發問，而后將問題“踢”給學生：“誰來幫助解答這個問題？”引發思考，使問題成為學生各階段學習的觸發點。

相信學生并平等對待他們，他們就敢于發問、勇于質疑、善于解疑。

有時，在出示課題階段，我們就可以問學生：看到這個課題，你知道我們這節課的學習內容是什么嗎？

比如，我出示課題“找質數”，學生問：“什么是質數？怎么找質數？”學習由此開始。

在教學過程中，學生又問：是不是所有的奇數都是質數，所有的偶數都是合數呢？

我說：“這個問題提的很好，大家一起來舉例比較一下吧。”

其實，學生提出這個問題，他自己一定就會往下思考。果不其然，這個學生最快舉手解釋了自己的問題：“不是所有的奇數都是質數，比如3、5、7等是質數，9、15等就是合數了，而1既不是質數也不是合數；除了2以外，所有的偶數都是合數。”

馬上又有學生問道：“那是不是所有的質數都是奇數，所有的合數都是偶數呢？”

學生的問題一個接著一個，教師不要去回答他的問題，而是將問題“還”給學生，讓他們自己去思考，由他們自己解決問題，更能激發他們的成就感。

黃愛華老師在上“圓的認識”時，將課題改成“井蓋為什么是圓的”，只講了不到10分鐘時間，就放手讓學生將自己想知道的問題自由上臺寫在黑板上。學生們寫了二十幾個問題，將黑板寫滿了，下課時間也到了，學生還意猶未盡。在與聽課老師的互動階段，黃愛華老師說：“學生能提出這些問題，其實他也能夠自己回答這些問題了。”之后，他還展示了這節課在全國十幾個城市教學時，學生提出來的各種問題。提出問題本身就能引發學生思考，一個個問題，就是一個個觸發點，將教學不斷往前推進。

二、議典型，鼓勵創造

《課程標準》指出：“評價不僅要關注學生的學習結果，更要關注學生在學習過程中的發展和變化。”

學生的想法，對學生來說，都是一種創造。將學生的典型創造放大，是對學生創造性的最大鼓勵，同時還可以使其成為課堂教學的生長點，一步步推進課堂教學，最終完成教學任務，實現教學目標。

學生的想法多數是再創造，有時也有原創造。教師要在巡視和交流中，了解學生的想法，并將典型的想法有序地提交給全班交流，“放大”這些想法，使這些想法成為一個個生長點，將教學一步步向前推進。

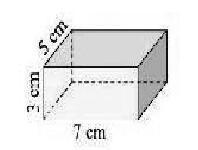
在“長方體的表面積”教學中，學生知道了長方體的表面積是指它6個面的總面積后，我就出示了課本中的情境和問題（如下圖）

學生自主解答，全班交流階段，我依次展示了以下想法：

1.逐個面計算，而后將6個面面積相加；

2.計算每相對的兩個面面積之和，而后將3組面面積相加；

3.（7×5+7×3+5×3）×2

借助這三種想法，同學們不但掌握了長方體表面積的意義，而且還能夠利用長方體相對面相等的特點進行列式計算，最后再應用乘法分配律進行簡便計算，部分同學還歸納出了計算公式。

從放心讓學生自己解答，到有序呈現，展示交流，再到歸納公式，學生的主體地位得到了充分體現。步步為營，依賴于學生的生成，課堂不斷生長，同時還培養了學生的創造意識和優化意識。

三、辨是非，強化認知

心理學家蓋耶認為：“誰不愿意嘗試錯誤，不允許學生犯錯誤，就將錯過最富有成效的學習時刻。”

學生在嘗試學習過程中，經常發生錯誤。教師要積極利用這些錯誤資源，組織學生討論，使學生在犯錯議錯糾錯的過程中，不斷強化概念、規則、規律，鞏固課堂知識。

下面這道題的計算錯誤是典型的：2.5×4÷2.5×4=1

我們可以利用這個錯誤，組織學生討論，進一步強化乘除混合運算的運算順序。

師：這道題的計算對嗎？為什么？

生的意見不一致。師讓他們自己討論，最后大家統一了意見：分數乘除混合運算，沒有小括號時，按從左到右的順序進行計算。這題的錯誤就在于改變了運算順序。

有學生反對，說：“如果應用乘法結合律就可以使計算簡便，答案就等于1啊！”

教師板書：2.5×4÷2.5×4=（2.5×4）÷（2.5×4）。問，是這樣嗎？學生回答說是。

教師又在“=”上寫了一個“？”

學生們立即展開討論，發現了問題，說“乘法結合律要在連乘中才能使用，這里是乘除混合運算，不能使用。”

有學生說：“那這題數字一樣，好像可以簡便啊！”

師問：“可以簡便嗎？”

學生再次展開討論，最后統一了認識：“2.5×4÷2.5×4=2.5÷2.5×4×4=16，題中本來是先乘4再除以2.5，但在乘除混合運算中，也可以先除以2.5再乘4，計算的結果不會改變”。

從一道錯題開始，層層剝筍，學生在討論中不斷產生問題，在問題解決中逐漸認識知識本質，認知因此得以鞏固和強化。

四、釋歧義，拓展思維

教學中學生往往會出現歧義甚至矛盾，教師不要急著做 “裁判”，而要及時捕捉這些矛盾，并組織辯論，使學生在辯論中應用知識、深化認識，拓展思維。

在教學“比的認識”時，學生舉出了許多生活中的比，其中有一個例子是：“2014年世界杯德國1：0勝阿根廷隊，奪得冠軍。”

我將這個例子也寫到黑板上，并不立即指出錯誤。

當教學到“比的后項不能為0”時，有學生問到：“那剛才舉例當中的足球比賽雙方比分為1：0，比的后項不就是0了嗎？”

我裝作為難的樣子：“嗯，是呀，這里比的后項不就是0嗎？”

就此，兩種不同意見的同學引用所學知識展開了激烈辯論。

“什么叫比？書上說了，兩個數相除，又叫做兩個數的比。而除法中的除數不能是0，所以比的后項也不能是0！”

“可這里1：0的后項不就是0了嗎？比賽中這種比經常見到！”

大家一下子陷入了困頓：比的后項肯定不能是0，但這里要怎么反駁呢？

我提示到：“比賽中的比，是我們數學里講的相除關系嗎？”

學生恍然大悟：“不是，這里是表示兩個隊的得分情況，不是相除關系。”

有同學總結道：“比賽中的‘比，名字和寫法都跟我們數學中的‘比一樣，但實際上表示的意義不一樣，不能混為一談。”

課堂教學經常會生成矛盾，這是一個很好的資源，在教師的組織下，同學們應用知識進行積極辯論，最后澄清了事實，統一了認識，并拓展了思維。

教學要有預設，但更要促進生成，這樣的課堂，是真實的、生動的、活躍的；應用不同策略，有效利用生成，這樣的課堂必然是靈動的、高效的、有價值的。

【參考文獻】

[1]《義務教育數學課程標準（2011年版）》.北京師范大學出版社，第50頁

[2]《義務教育數學課程標準（2011年版）》.北京師范大學出版社，第52頁