風險平價方法在中國市場的實證研究

一、引言

資產配置的研究對于金融經濟行業來說有著重要的意義。

等權法(1/N)是最古老的資產配置方法。兩千年前，《塔木德》一書中便記載了這種思想，“每個人應該將自己的資產分成三個部分，其中1/3投資于土地，1/3投資于商業，另外的1/3作為現金儲備”。等權法并不對任何參數進行預測，而只是簡單地對資本進行平均分配，卻因為其極簡的操作和優秀的業績，至今在資產配置實踐中保有其活力。

現代的資產配置理論起源于Markowitz(1952)提出的均值-方差模型(Mean-Variance Optimization，MVO)，通過輸入預期的各項資產收益率和協方差矩陣，在組合預期收益率給定的情形下，選擇使得波動率最小的資產組合。它開啟資產配置量化先河，許多新的資產配置模型皆是建立在其思想之上。

然而MVO在實際應用中效果并不能好于1/N，BernartzisndThaler(2001)，Windcliff and Boyle(2004)和DeMiguel(2009)的實證研究都證明了等權法在股市上的超凡表現。DeMiguel(2009)認為，雖然MVO是一種最優化的方法，理論上能夠最大化資產配置效率，但是實踐中由于輸入參數的估計誤差較大，抵消了最優化帶來的好處。

人們試圖在減輕估計誤差和提升配置效率之間進行權衡。由于MVO的配置結果對于收益率的預測結果十分敏感(Michaud，1989)，且對資產波動預測的準確性遠高于對資產收益率的預測準確性(Merton，1980)，所以MVO的估計誤差主要來自于收益率預測。也因此，一些僅僅根據風險指標進行資產配置的方法得到青睞，如最小方差法、風險平價法。

最小方差法(Minimum Variance，MV)是均值-方差方法的特解，它并不需要直接利用收益率的預測，而只需要根據各項資產的方差、協方差，試圖最小化整體波動。Chopra andZiemba(1993)的研究表明，運用MV得到的組合優于輸入收益率預測并通過MVO計算出來的資產組合。Clarke andThorley(2006)的研究指出，其構建的MV組合收益率優于市場組合，而風險卻只有市場組合的3/4。MV較之MVO，由于不直接考慮預期收益率的情況，而在最優化效率上有所降低，但同時估計的誤差也大大降低，導致總體來說MV實證表現優于MVO；但是其在資本市場的表現仍舊未能超越1/N。MV只考慮組合風險最小化，卻并未考慮風險在各個資產之間的分配。

風險平價法(Risk Parity，RP)的核心思想是將每種資產按風險貢獻平均分配，這實際上是資產配置的應有之義。20世紀90年代中期，RP已經作為一種經驗法則被應用于資產配置實踐中，但是直到2008年金融危機后，才因為其在危機中優秀的表現而聲名大噪，得到更多研究者的關注。

股債二元情形下，60/40組合中雖然債類資產占總資產的40%，但是實際上超過90%的波動是來自權益資產，風險分散效果并不好；而通過RP組合中對債類給予較大權重，從而可以達到近似的風險平均分配，再通過杠桿實現目標收益率。Edgar Peters(2011)指出，RP方法的優越性體現在權重的分配是波動性的函數，當波動性大的時候RP方法會給權益資產更小的權重，而在波動性小的時候會給股票更大的權重，而在波動性大的時候，債類資產往往表現得比權益資產更優。Maillard，et al. (2010)研究發現，從1995直到2008年，RP方法的表現始終優于1/N法。Ruban andMelas(2011)在股債二元情形下對比了RP和60/40，并對比了二者的收益率之差，發現在互聯網泡沫中，60/40遠好于RP；但是當互聯網泡沫破滅后的一個階段，RP顯示出驚人表現。Chaves et al.(2011)在更廣闊的時間區間上，發現RP并不總是優于60/40或1/N，但是它幾乎總是優于最小方差法。

必須注意的是，根據歷史數據做出的實證研究結果并不能成為各種方法孰優孰劣的絕對判斷，因為實證研究中，結果對很多因素敏感，如資產池的選取、時間段選取、評價指標等。舉例來說，Chaves et al.(2011)中RP方法表現較差的時段大多在1980-1999期間，而這些時間段剛好大多都在Edgar Peters(2011)研究的樣本期外。Chaves et al.(2011)的敏感性分析指出，選取不同的資產池對于RP實證的結果有很大的影響，但是不幸的是，我們并沒有很好的范式來指導資產池的選取。

這些研究給我們兩點啟示，1、實證研究的目的在于加深我們對RP方法優劣勢的了解，及其適用的情形，而并非為了在賽馬式比較中得出一個絕對的最優策略；2、市場情況變化多端，我們仍需要不斷跟蹤進行更多的實證研究。

在中國市場上，基于RP的大類資產配置策略能夠提供比其他資產配置方法更為穩定的長期業績(蔡文捷，2017)；RP在A股市場行業配置上亦有較強的適用性，甚至超越了等權法(鮑兵，2014)。但是總體而言，RP方法應用于中國資本市場的實證研究是不足的。

本文的研究目的是，將RP與其他方法在中國市場上做賽馬式實證研究，以彌補中國市場上RP的實證研究不足的現狀，并檢驗Edgar Peters(2011)、Maillard，et al. (2010)等人在美國市場上的研究結論移至中國市場是否仍舊成立。

另外，本文在對于賽馬式分析的基礎上，創新性地對這些方法分別從債類、權益類資產的選擇以及方差-協方差矩陣的輸入進行了敏感性分析，以檢驗實證結論在我國市場的穩健性。

本文總共分為四部分：第一部分為引言，綜述資產配置方法，尤其是風險平價方法的理論和實證研究進展；第二部分為實證方法概述，對本文使用的數據、資產配置方法的具體算法、業績度量指標進行介紹；第三部分展示風險平價方法在中國市場的實證研究結果，分為股市行業配置與股債二元配置兩方面進行，對風險平價法(RP)、等權法(1/N或60/40)、最小方差法進行賽馬式實證研究，并進行時間區間和資產池的敏感性研究；第四部分為結論與展望，本文在對風險平價法的理論闡述和實證研究的基礎上，得到其在中國市場上表現的實證結論，并且對于本文研究的局限與后續研究方向作出一定探討。

二、實證方法概述

數據概覽

實證部分所有數據均來自于Wind資訊終端。

在中國股票市場構建RP和其他方法的賽馬式實證研究時，選取WIND一級行業指數，共11個行業，分別是能源、材料、工業、可選消費、日常消費、醫療保健、金融、信息技術、電信服務、公用事業、房地產。樣本期間為2006年1月1日至2017年12月31日。11個行業指數在樣本期間的描述統計情況如表1所示。在2006-2017年間，總體來看，月平均收益率最高的行業是醫療，最低的行業是能源；波動率最低的行業是日常，最高的行業是房地產；夏普率最高的行業為醫療，最低的行業為能源。另外，可以發現11個行業之間的相關性是比較高的，最低也達到0.61，最高為0.96，且任意兩個行業的相關系數均大于0.5，說明各行業之間的聯動性很大。

在中國市場研究股債二元配置時，使用滬深300代表股市，中證全債代表債市；并在敏感性分析中換之以上證綜指、上證國債作為替代。樣本期間為2006年1月1日至2017年12月31日。滬深300、上證綜指、中證全債、上證國債在樣本期間的描述統計情況如表2所示；對四種指數作歸一化處理，基期設為2006年1月1日，則得到二者的凈值變化如圖1所示。

表1 WIND一級行業11種指數統計描述

相對于債券指數，股票指數的收益率和波動性都較大，但是債券指數的夏普率相對較高，這與美國市場的情形是一致的。股指與債指之間相關系數為負，適合構建資產配置策略的資產池。

表2 所使用股指與債指統計描述

圖1 所使用股指與債指歸一化凈值對比

另外，在計算資產權重時，每20個交易日進行一次權重的計算，并在第21天進行調倉，重新配置資產，每次測算的觀測期定為測算期往前推100個交易日，即將前100日估計的樣本方差-協方差作為輸入變量，通過不同方法進行權重計算。不斷重復該過程得到權重序列。

資產配置方法

1.風險平價方法(RP)

風險平價法在配置資產時，不需要將收益率因考慮在內，僅僅包含風險因素。其基本的思想是每種資產對于風險的貢獻是一樣的。考慮單個資產之間的協方差關系，我們首先定義每一種資產的總風險貢獻TRC(totalriskcontribution)：

風險平價方法要求各個資產對于組合整體的風險貢獻相同，也即：

定義方差協方差矩陣為∑，則上述等式寫作矩陣形式為：

2.最小方差法(MV)：

對比可知，MV致力于保證各個資產的邊際風險貢獻一致，而RP是保證了各個資產對于總風險的貢獻一致。

具體操作中，使用Matlab中Quadprog庫解決如下二次規劃問題：

minwT∑w，s.t.w=1

其中Σ表示方差協方差矩陣。

3.等權法(1/N與60/40)

本次實證中還采用了等權法作為參照。

在股市的行業配置研究中，1/N法計算出的每種資產占用總資本的比重：

在股債二元配置問題上，60/40法是基于傳統的1/N的方法的一種變體，部分偏離原來的50/50結構，即將60%的資本配置在權益類資產，40%的資本配置在債類資產上：

wequity=0.6

wbond=0.4

(三)業績度量指標

本文中，績效評價指標選用夏普率，其計算公式如下：

其中收益率和標準差均按日計算，并作年化處理。無風險利率以銀行間市場7天回購利率(R007)測度，并進行動態計算。

夏普率測度投資者承擔一單位風險得到的超額回報，使得不同波動的資產組合收益亦可以加以對比，夏普比較高的組合，其績效越好。

三、實證結果

(一)A股市場行業配置

選取Wind一級行業分類11項股指作為資產池，分別使用等權法(1/N)、風險平價法(RP)、最小方差法(MV)、跟蹤滬深300(equity)四種方法進行對比研究。圖2是四種策略的歸一化凈值變化對比，同在A股市場，11種行業指數之間相關性大，且與股票市場的相關性較大，故而四種策略構建的組合差異性不明顯。

圖2 股市行業分配2006-2017年 1/N、RP、MV、equity歸一化凈值對比

觀察全時期的指標(表3)，RP組合夏普率位居第二，相對于市場組合有較大增強，其收益率亦高于市場組合；但是無論收益率、波動率還是夏普率都次于MV組合；RP組合與1/N表現接近。

通過觀察RP、MV組合權重分配隨時間的變化(圖3左)，可以發現RP權重接近于1/N分配，而MV組合調整持倉更為頻繁(圖3右)，這將導致更大的交易成本。綜合權衡二者孰優孰劣仍有待進一步量化研究。

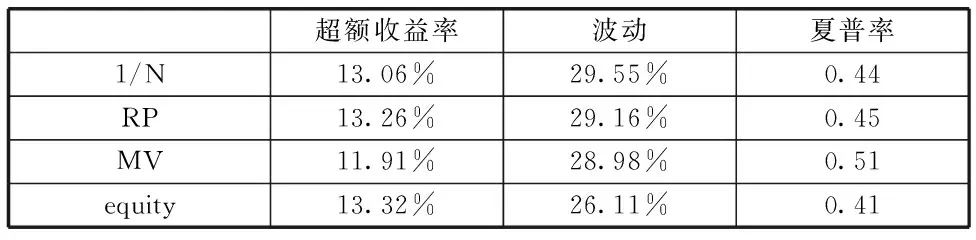
表3 股市行業分配2006-2017年全時期1/N、RP、MV、equity夏普率對比

圖3 RP(左)與MV(右)資產權重時間序列

具體考察四種組合每一年度的夏普率指標(圖4)，沒有一種策略絕對占優，1/N、RP、MV策略相似且在多數時間略優于市場組合。RP方法并沒能顯示出其優越性，原因就在于資產池中的11類行業之間較大的相關性，由于資產池自身的局限性，導致資產配置方法之間不能顯示出區別性和各自優劣勢所在。而當我們轉而進行股債二元配置時，差異性才體現出來。

圖4 股市行業分配2006-2017各年度1/N、RP、MV、equity夏普率對比

(二)大類資產配置之股債二元研究

我們使用滬深300、中證全債代表股債二元，并使用60/40、風險平價法(RP)、最小方差法(MV)三種方法進行賽馬式對比實證研究。

從圖5直觀來看，RP、MV組合凈值波動較小，在2006-2017的樣本期間呈現平穩上升趨勢，而60/40組合凈值波動劇烈，與股市聯動性較大。

考察三種策略組合的夏普率(表4)，RP組合在整個樣本期具有最高的夏普率(0.91)，MV組合次之(0.75)，60/40組合雖然具有最高的超額收益率，但是由于其波動相對更大，導致60/40組合的夏普率僅有0.37。

圖5 股債二元分配2006-2017年60/40、RP、MV歸一化凈值對比

超額收益率波動夏普率60/406.30%16.99%0.37RP1.87%2.05%0.91MV1.27%1.71%0.75

按各年度子樣本計算三種方法的夏普率并進行更進一步的對比(圖6)。

首先，將RP組合與60/40組合進行對比，可以更明顯地發現60/40組合與股市的聯動性，其在股市向好的年份(2006、2007、2014、2017年)表現優越，而在股災或說股市表現低迷的年份(2008、2011、2012、2015年)則均產生了負的夏普率，也即，在這些年份，60/40組合的平均收益率未超過無風險利率。相比之下，RP組合在股市向好的年份雖有超過無風險利率的收益率，但其夏普率表現不如60/40組合，但是RP組合在股災年份卻能夠保持堅挺，顯示出其避險作用。

第二，將RP組合與MV組合進行對比，MV組合在股災來臨時的夏普率表現更優于RP組合，然而由于其一貫過于穩健保守的策略風格，使得其績效在股市更好的年份中(2007、2009、2017年)表現平平。MV組合雖然亦有避險作用，但是相比于RP，其夏普比在股市表現較好時，則會明顯次于RP組合，總體來看其表現在年份間也有相當大的起伏。

總的來看，無論是在金融危機、股災期間，還是在平時，亦或是股市高昂的時候，RP組合表現出中等的避險能力與收益能力。具體地，在未來股債市場走勢未知的情形下，就避險與收益能力來看，60/40組合更為激進，更注重可能的收益；MV組合則極度保守，更注重可能到來的股災；RP組合則顯得更為中和，總是得到一個介于60/40組合與MV組合之間的夏普率。

圖6 2006-2017各年度60/40、RP、MV夏普率對比 (滬深300+中證全債)

進一步把兩種資產的風險貢獻量化為：

后驗計算不同策略中每種資產對于整體風險的貢獻比例(圖7)，可以發現，60/40策略幾乎所有風險全部來自于股市，而MV組合風險則大抵來自債券，RP組合的風險在兩種資產之間則有更加平均的分配。如果允許賣空(圖8，RP_without_res)，可以更清楚地看到，RP組合的風險在兩種股債資產之間的分配接近50/50均分。后驗風險貢獻占比的對比圖也能更好地展示出RP組合的在風險分配方面，介于60/40組合與MV組合之間的中和性質。

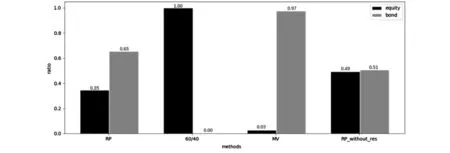
圖7 后驗風險貢獻占比

對于交易成本的研究，我們選擇兩個指標進行，第一個指標是每一次權重指標調整的絕對值的均值(AVE-ABS)，第二個指標是樣本期間所有權重的標準差(STDEV)，以反映權重的波動，而權重的波動正是代表每一次交易的量，所以在一定程度上，對于權重的波動性研究，可以反映其交易成本的變化。由于60/40的權重樣本區間不會發生變化，所以交易成本最小。其結果如表5。

兩種指標指向的結果是一致的，即，RP策略的換手率高于MV策略，從而RP方法將產生更多的交易成本。RP策略之所以產生較高的換手率，或許是因為其較MV策略更主動積極的調整所致。據Edgar Peters(2011)，當波動性大的時候RP方法會給予權益資產更小的權重，而在波動性小的時候會給股票更大的權重；在波動性大的時候，債類資產往往表現得比權益資產更優。相比于RP對于市場情況積極調整權重的策略，MV策略總是追求組合整體風險的最小化，因而債類資產總是保持在高位且較為穩定的權重(圖8)。

表5 RP與MV交易成本簡易對比

圖8 RP與MV權重時間序列

除滬深300+中證全債之外，本文進一步選取了滬深300+上證國債、上證綜指+中證全債兩組資產池，按照之前同樣的研究思路，進行對資產池的敏感性檢驗。

從2006-2017年總體的夏普率數據來看(表6)，RP組合與MV組合的夏普率總是遠高于60/40組合，然而RP組合和MV組合的優越性對比結果對于不同的資產池敏感。在滬深300+上證國債的資產池下，MV的總體夏普率(0.81)超越了RP組合(0.79)，而在滬深300+中證全債、上證綜指+中證全債的資產池下，RP總體的夏普率總是優于MV組合。

表6 資產池敏感性分析之全時期1/N、RP、MV夏普率對比

具體到每年夏普率對比圖(圖9、10)，可以觀察到，上證綜指+中證全債逐年夏普率的對比圖與前文近無不同，而滬深300+上證國債的組合略有差異。然而，總體來說，上文結論對不同資產池是穩健的，即，從避險能力和收益能力的權衡來看，RP組合確實更為中和，一般總是得到一個介于60/40組合與MV組合之間的夏普率。但是如果要在三種組合之間分出孰優孰劣，恐是不審慎的。

圖9 2006-2017各年度60/40、RP、MV夏普率對比 (滬深300+上證國債)

圖10 2006-2017各年度60/40、RP、MV夏普率對比 (上證綜指+中證全債)

四、結論與展望

通過風險平價方法和等權法、最小方差法在中國市場的對比實證研究，我們可以得出結論：

1.若是在股市范圍內做行業配置，RP組合從權重分配上看近于1/N組合，夏普率表現略優于1/N組合；RP組合夏普率表現不如MV組合，但是由于MV組合換手率較高，由此產生較高的交易成本，孰優孰劣有待進一步研究。總體而言，由于股市行業間聯動性強，三種方法差異性難以體現，在此語境下談論資產配置方法對比意義不大。

2.股債二元配置實證結果表明，并不能武斷地擇出一個在所有時期都占優的資產配置策略，每種策略有其不同的側重。就RP策略而言，從避險能力和收益能力的權衡來看，其相較于60/40策略(更注重潛在收益)和MV策略(更注重潛在風險)更為中和，一般總是得到一個介于60/40組合與MV組合之間的夏普率。

由于中國市場較為年輕，無法如同國外的實證研究一般回溯多個經濟周期的歷史數據，研究結果是否長期有效亦有待進一步的觀察和檢驗。本文可以進一步深入研究的方向有：進一步擴大研究中資產池以觀察結論對資產種類的敏感性；選擇多種方差-協方差矩陣估計方法檢驗敏感性；提高權益資產對組合整體的風險貢獻比例(RP-Enhanced方法)參與對比；對于交易成本進行量化的分析并從收益中扣除。