融合K均值聚類和低秩約束的屬性選擇算法

楊常清

(西安航空學院 材料工程學院, 陜西 西安 710077)

0 引言

高維特征雖然可以準確多樣化地表現物體特性，但使用高維數據不僅增大存儲空間，還增加運算復雜度。對高維數據進行屬性約簡，降低數據維度，挖掘數據內部具有代表性的低維屬性，已成為機器學習的一個研究熱點[1-2]。

屬性約簡的優點包括能降低處理時間和得到更具有泛化能力和更堅實的學習模型等[3-4]。常見的屬性約簡方法包含子空間學習和屬性選擇兩種方法。子空間學習是把高維屬性從高維空間投影到低維空間，并保持數據間的關聯結構，而屬性選擇是從原始屬性集中選擇最能代表整個屬性集的屬性。利用多方向理論，學者們提出了各種屬性選擇算法。文獻[5]將知覺理論赫姆霍茲原理作為特征選擇的度量，用于文本分類的特征選擇中，取得了較好的效果。文獻[6]將類特定變換的新型語義平滑核融入支持向量機模型中, 提出了一種使用語義分類方法來構建高性能的半監督文本分類算法。文獻[7] 將皮爾森相關系數(RRPC)的最大相關和最小冗余準則用于半監督學習方法中，利用增量搜索技術來選擇最優特征子集，平衡了文本特征提取中冗余特征與計算量間的矛盾。文獻[8]提出了一種基于圖稀疏的自表達屬性選擇算法。文獻[9]提出了一種基于稀疏學習的低秩屬性選擇算法，通過嵌入子空間學習方法來調整屬性選擇結果。文獻[10]在經典粗糙集絕對約簡增量算法的基礎上，提出了一種快速屬性選擇算法，快速有效地對大規模數據集進行屬性選擇。文獻[11]提出了一種多變量時間序列的無監督屬性選擇算法，有效解決了大數據集無類別信息問題。文獻[12]在卷積神經網絡算法中引入無監督特征學習方法，實現了無監督的特征學習方法。文獻[13]提出了一種基于蟻群優化的無監督特征選擇方法,該方法試圖通過幾次迭代找到最優特征子集，而不使用任何學習算法，并根據特征之間的相似性來計算特征相關性，從而導致冗余度的最小化。文獻[14]從無標注藏文語料中抽取邊界熵、鄰接變化數、無監督間隔標注等特征，并融入有監督的序列標注藏文分詞系統,實現了無監督特征的藏文分詞。如何在無監督屬性選擇中利用類別信息選擇屬性是當前需要解決的難題。本文借鑒聚類算法、子空間學習和屬性選擇各自的優點，提出一種有效的屬性選擇算法。

1 算法描述及推演

1.1 算法描述

本文算法在線性回歸的模型框架中有效地嵌入自表達方法,同時利用K均值聚類產生偽類標簽最大化類間距以更好地稀疏的結構；其次，在新模型中有效融合低秩約束的屬性選擇，即利用稀疏學習方法中的l2,p-范數參數p靈活控制結果的稀疏性。

設給定訓練集A=[a1,a2,...,an]∈Rn×d，類標簽矩陣B∈Rn×k，回歸系數矩陣C∈Rd×k，采用線性回歸模型如式(1)所示。

(1)

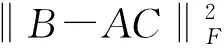
C=(ATA)-1ATB

(2)

任何數據集或多或少都有冗余屬性，而頗具代表性的屬性往往蘊含數據的空間和類別信息，為了著重凸顯數據的獨特屬性，本文引入低秩來滿足實際數據集合中的非滿秩需求。線性回歸模型可對每類響應變量分別求解，這種求解忽略了響應變量間的相關性，為此，利用低秩約束回歸系數矩陣C,如式(3)所示。

rank(C)=r,r≤min(d,k)

(3)

在式(3)上，利用屬性自表達方法把A作為響應矩陣，將問題轉化為式(4):

(4)

為了使算法獲得較好的分類效果，本算法利用K均值聚類將樣本聚類到偽類標簽中，以最小化類內距離和最大化類間距離。

假定m個類中心，變換后的聚類中心矩陣G=[g1,...,gm]∈Rd×m，利用K均值聚類最小化如下目標函數，如式(5)所示。

(5)

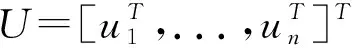
根據bi=aiC，通過回歸系數矩陣C的線性轉化，可得類內最小間距。把式(5)代入式(4)中可得式(6):

s.t. rank(C)≤min(d,k)

(6)

式(6)回歸系數矩陣C∈Rd×k具有低秩約束結構，所以式(6)具有監督分類功能。

lF-范數對噪聲和離群數據較為敏感，因此可將lF-范數嵌入到模型中作為正則化項，以此來去除噪聲和冗余屬性，如式(7)所示。

(aiCi-uiGT)

rank(C)=r≤min(d,k)

(7)

式(7)中β為正參數，調節正則化項對模型的懲罰。通過調節參數，在使回歸系數矩陣C中不相關或弱相關屬性收縮為零的同時，能使重要屬性獲得更大的系數權重。

秩最小化是一個非凸優化且NP問題，但秩約束目標函數是可解的，即全局解能夠得到[15]。為了更好地優化低秩結構和有效考慮類別間關聯結構，算法令C=XY，并且有低秩r，則目標函數為:

s.t. rank(XY)≤min(m,k)

(8)

式(8)中，A∈Rn×d,X∈Rd×r,Y∈Rr×d，重構的回歸系數矩陣C、矩陣X、Y都是低秩結構。U、G分別表示聚類指示矩陣、聚類中心矩陣，‖.‖F表示矩陣弗羅貝尼烏斯范數。

1.2 目標函數優化

由于式(8)的前半部分是凸的，lF-范數雖然對噪聲和離群數據較為敏感，但作為正則化項它是非光滑的，為了高效率地求解目標函數(8),本文通過固定不同矩陣依次優化的方法來最優目標函數(8)。首先將式(8)化簡，如式(9)所示。

βTr(YTXTDXY)

(9)

式(9)中D∈Rd×d為對角矩陣，其每個元素定義如式(10)所示。

(10)

ci表示矩陣C*=X*Y*的第i行，X*、Y*、C*分別為X、Y、C的最優解。

本文通過固定不同矩陣，依次優化對應矩陣，逐步實現最優目標函數的目的，其具體操作過程如下。

(1) 固定矩陣X、Y、G，優化矩陣U

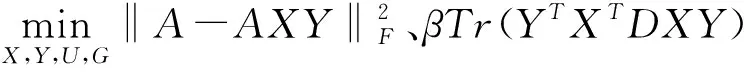
(11)

根據式(11)可知，經AXY原始數據轉換后，再K均值處理，可使轉換后的數據都分配到標簽。

(2) 固定矩陣U、X、Y,優化矩陣G

當固定矩陣U、X、Y后，對式(9)的優化矩陣G求偏導數，并令所得偏導數為零。

(12)

(3) 固定矩陣U、G,優化矩陣X、Y

固定矩陣U、G，將式(12)代入式(9)中，并令式(9)等于E，可得:

(13)

通過上述化簡，目標函數(8)就轉化為:

(14)

令H=ATA-αATU[(UTU)-1]TUTA+αATA+βD，通過優化矩陣X、Y，同時證明本文算法具有執行線性判別分析[16](linear discriminant analysis, LDA)的特點。

1.3 目標函數推理

經過1.2節的目標函數優化，將式(8)轉化為式(14)，但通過式(14)無法求解函數的最優值，本節通過對式(14)繼續推理，以期證明式(14)具有執行LDA過程的特點，構建全局最優與屬性向量間的橋梁。

固定聚類指示矩陣U和聚類中心矩陣G，對式(14)中的Y求偏導數，并令偏導數為零，如式(15)所示。

(15)

由式(15)可得YT=ATAX[(XTHX)-1]T，把得到的矩陣YT和Y代入式(14)中，有:

(16)

根據式(16)的推導，目標函數E只含有變量X，優化問題轉化如下:

其中Qt和Qb分別表示LDA類內矩陣和類間離散度矩陣。通過求解式(17)可得矩陣X的最終表達式如式(19)所示。

(19)

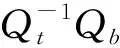
由于系數矩陣最優解C*=X*Y*的列空間和X的列空間相同，所以本文提出方法與正則化LDA具有同樣的列空間。

2 本文算法及其收斂性

本文借鑒聚類算法、子空間學習和屬性選擇各自的優點，提出一種有效的屬性選擇算法。在線性回歸的模型框架中有效地嵌入自表達方法,利用K均值聚類產生偽類標簽最大化類間距以更好地對結構進行稀疏化處理；運用l2,p-范數考慮屬性及其對應響應變量間的相關性，利用低秩約束來考慮不同類別間的相關性，消除數據冗余和不相關屬性，以實現最優屬性子集的選擇。算法偽代碼如下:

算法1: 本算法偽代碼Input: 訓練數據集A;正則化參數α,β;支持向量機參數(m,g)∈[-10: 2: 10];步驟1: 初始化分類器,類型選擇線性模式;步驟2: 通過自表達方法得到自表達矩陣A;步驟3: 根據模型(8): 調用算法2求解全局最優解,以求自表征矩陣C*=X*Y*;步驟4: 利用最優解C*對原始屬性集A進行屬性選擇,利用得到屬性集更新樣本屬性集;步驟5: 采用支持向量機對新屬性樣本分類;Output: 分類準確率。

算法2: 優化求解式(8)的偽代碼Input: 數據集A;參數α,β,r聚類中心數m;控制參數p;步驟1: 初始化 t=0,矩陣X(t)和Y(t),得到初始化C(t)=X(t)Y(t);步驟2: 利用K均值算法初始化矩陣U(t),初始化D(t)∈Rd×d; Do 步驟3: 通過公式(11)計算U(t+1); 步驟4: 通過公式(12)計算G(t+1); 步驟5: 通過公式(15)計算Y(t+1); 步驟6: 通過公式(19)計算X(t+1); 步驟7: 更新對角矩陣D(t+1),利用公式(10)計算第i個對角元素,ci=[X(t+1)Y(t+1)]i,t=t+1;While 目標函數(8)收斂;Output: 矩陣X,Y,聚類指示矩陣U。

對于迭代算法，收斂性是算法是否健壯有解的性能指標，對于本文提出的目標函數式(8)和其中的正則化項都非平滑，并且式中需要優化四個變量，求解目標函數最優解難度頗大，但首先要證明本算法是否收斂。

當迭代次數為t時，根據算法2中的步驟可知:

當迭代次數為t+1時，根據式(11)規則固定矩陣更新優化U(t+1)，可得如下不等式:

(22)

當迭代次數為t+1時，根據公式(14)規則固定矩陣U(t+1)，優化更新矩陣X(t+1)、Y(t+1)、G(t+1)可得如下不等式:

(23)

聯合不等式(22)和(23)可得:

(24)

通過式(24)可知，目標函數是單調遞減的，因此多次迭代后可收斂。

3 仿真實驗分析

3.1 實驗數據集

將本文算法、NFS(non feature selection)算法、LDA算法[16]、RFS算法[17]和RSR算法[18]等五種算法在BASEHOCK、PCMAC、Smk-can、ecoli-uni、CNAE-9、warpPIE10六個數據集上進行仿真，其中數據集ecoli-uni和CNAE-9屬于UCI[19]，Smk-can、PCMAC、BASEHOCK、warpPIE10來自數據集[20]，數據集詳見表1。

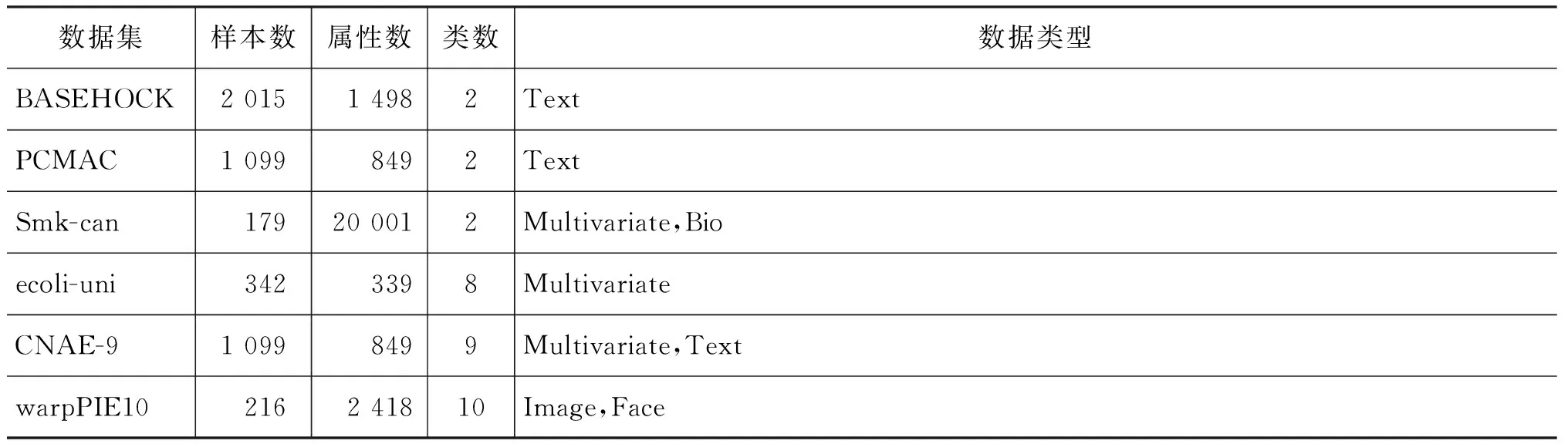
表1 數據集信息統計

仿真實現的環境及配置如下: 仿真是在Windows 7系統下，CPU: i3-3240@3.4GHz,RAM: 4GB，使用Matlab 2014a軟件進行編程實現。

3.2 實驗結果和分析

本文采用十折交叉驗證法將原始數據分成訓練集和測試集，再利用SVM進行分類，同時，把需要定義作為評價指標，即分類準確率越高表示算法效果越好。所有算法均保證在同一實驗環境下進行，最后提取十次運行的實驗結果的均值加減均方差來評估各算法的性能，以此評估實驗的穩定性，各算法在數據集上的結果如圖1所示。

通過圖1(a)～(f)可以得出: 隨著交叉驗證次數的增加，本文算法在有些數據集上的分類準確率并不是最好的，但經過十次實驗得到的平均準確率要比其他四種算法高。為了更直觀地對比各算法的分類準確率，將各算法的分類準確率(均值±方差)統計結果列表，如表2所示。通過分析表2可以發現在所測試的六個數據集上，本文算法分類準確率均好于其他四種對比算法。與NFS算法、文獻[16]、文獻[17]和文獻[18]相比，分類準確率平均提高了17.04%、13.95%、3.6%和9.39%。

從方差上看，本文算法的方差在大多數數據集上是最小的，說明算法分類準確率是穩定的。但在數據集CNAE-9上，文獻[18]的方差要比本文算法的方差小4.2%，但分類準確率卻高出文獻[18] 9.39%，總體上好于文獻[18]。作為有監督屬性選擇算法的文獻[17]，因其利用現有的類標簽在類少數據集上取得了較好的分類結果，平均分類準確率為84.17%，尤其在多類數據集上，文獻[17]相比其他三種算法不僅利用偽類標簽進行分類，還利用線性判別分析數據間相關性，利用數據相關性甄別最優屬性子集。文獻[18]利用原始數據得到的自表達系數矩陣嵌入稀疏學習模型中進行屬性選擇，但由于算法為無監督屬性選擇，實際分類效果一般，平均分類準確率僅為79.32%。本文算法在線性回歸的模型框架中有效地嵌入自表達方法,同時利用K均值聚類產生偽類標簽最大化類間距，以更好地對結構進行稀疏化處理，并利用稀疏學習方法中的l2,p-范數參數p靈活控制結果的稀疏性，取得了較高的分類準確率，實際平均分類準確率為87.54%。

圖1 各算法在不同數據集上的結果

表2 分類準確率(均值±方差)的統計結果單位: %

不同數據集有不同的數據分布和干擾因素，像ecoli-uni、CNAE-9、warpPIE10等多類數據集，可通過控制秩大小來得到分類識別率，本文在數據集上的分類結果如下:

通過圖2(a)～(c)結果可知，具有低秩約束的本文算法相比滿秩得到的分類結果更優，結合表2綜合分類結果可以看出，在多類數據集上，本文算法具有更佳的分類準確率和穩定的識別率，這是由于本文算法不僅能提取到數據集的重要屬性，還能利用子空間學習對重要屬性進一步微調，保證了數據自身結構。

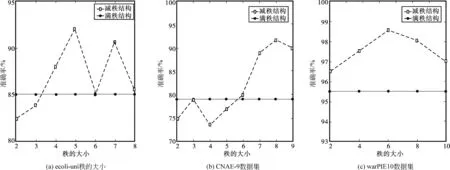
圖2 多類數據集分類結果

4 結束語

對無監督屬性選擇算法無類別信息和未考慮屬性的低秩問題，本文提出一種新屬性選擇算法。算法使用原始數據構建自表達矩陣，并融合K均值聚類、低秩屬性選擇和子空間于模型中，利用K均值聚類補充無監督選擇的缺陷，同時擴展子空間學習在回歸模型上的應用，彌補屬性選擇在數據調整中的不足。經實驗驗證，與其他四種屬性選擇算法相比，本文算法不僅有較高的分類準確率，并且分類結果也最為穩定，特別相比滿秩得到的分類結果更優。