基于時間序列的酒類飲品人均需求量預測

孟雪

摘要：酒類飲品是當今社會人民不可缺少的飲品及社交工具，酒類產(chǎn)品的生產(chǎn)與銷售也成為行業(yè)重要的組成部分。本文利用求和自回歸移動平均模型進行擬合，利用差分運算、ADF檢驗、ACF、PACF圖等方法，得到一個與時間相關的擬合方程。該模型通過了白噪聲檢驗。預測未來三年的酒類產(chǎn)品人均需求量，2007年～2009年，酒類產(chǎn)品人均需求量在（2.389372，2.526629）、（2.360950，2.555051）、（2.339141，2.576860）區(qū)間內。故酒類產(chǎn)品人均需求量在未來三年內平穩(wěn)且不下降的可能性較大，在生產(chǎn)和銷售過程中，應采取較為適中的銷售方案。

關鍵詞：時間序列；求和自回歸移動平均模型；差分運算；酒類產(chǎn)品人均需求量

在市場營銷活動中，預先知道產(chǎn)品未來幾年的需求量是十分有利的。本文通過對1890年至2006年的酒類飲品的年人均需求量的記錄，運用求和自回歸移動平均模型研究酒類飲品的年人均需求量規(guī)律，并預測未來三年的需求量。

一、數(shù)據(jù)來源

本文數(shù)據(jù)來自Time Series Library 酒類產(chǎn)品1890年至2006年人均需求量數(shù)據(jù)。

二、分析與結果

（一）模型求解

1.平穩(wěn)性檢驗

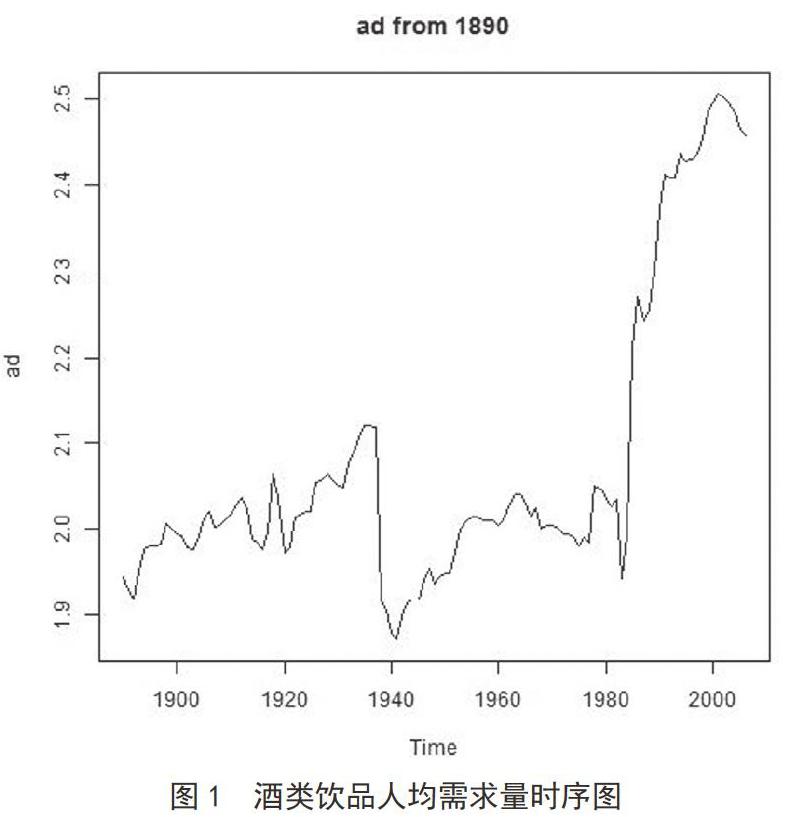
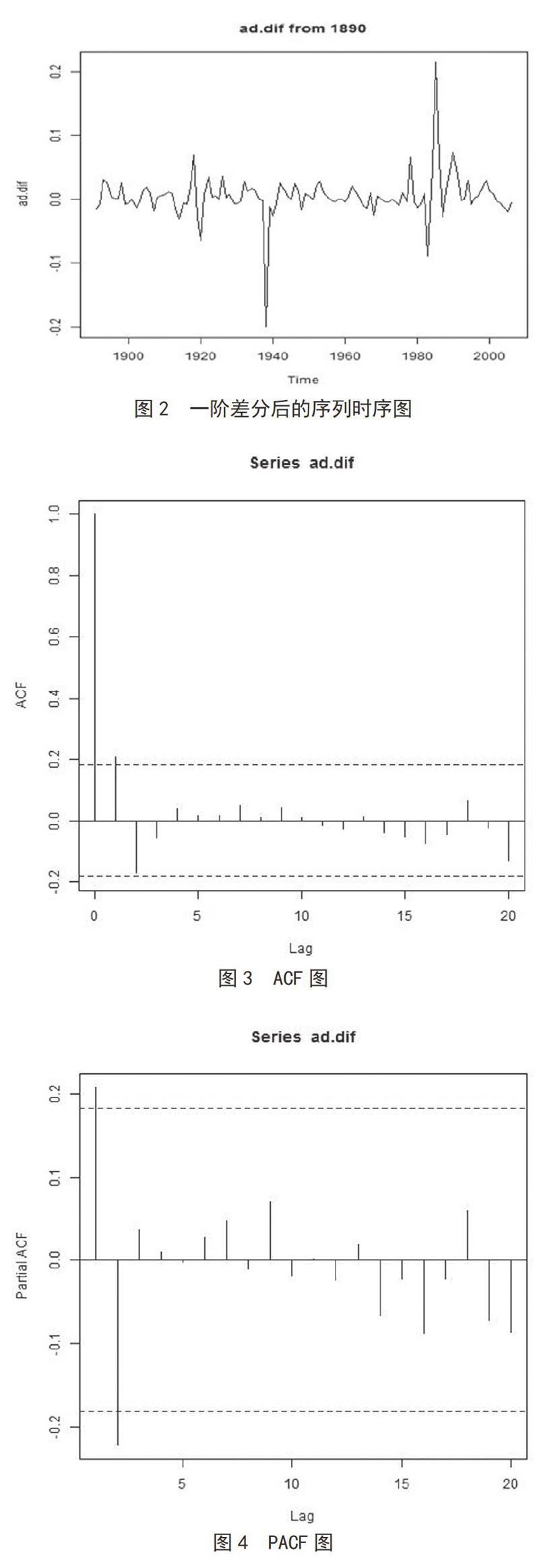
將搜集的數(shù)據(jù)繪制時序圖，進行ADF檢驗。繪制的時序圖如圖1所示。酒類飲品需求量是一個非平穩(wěn)序列。結果顯示，p值高達0.9，是非平穩(wěn)的。故對原序列進行一階差分，結果顯示一階差分后的p值小于0.01，所以一階差分后的序列就是平穩(wěn)的，差分后的時序圖見圖2。

2.模型的選擇

將ACk記為一些列觀測值（Yt）和k時期之前的觀測值（Yt-k）之間的相關性。繪制自相關函數(shù)圖、偏自相關圖，如圖3、圖4所示。可以確定模型為ARIMA（0， 1， 1）模型。

3.模型擬合

擬合ARIMA模型，這里指定了d=1，即函數(shù)將對序列做一階差分，因此我們直接將模型應用于原始序列即可。函數(shù)可以返回移動平均項的系數(shù)以及模型的AIC值。本文得到移動平均項的系數(shù)為0.3192，標準誤為0.0975，可以得到ARIMA模型的Θ（B），AIC值= - 452.19。如果我們還有其他備選模型，則可以通過比較AIC值來得到最合理的模型，比較的準則是AIC值越小越好。本文嘗試擬合了ARIMA（1， 1， 1）模型，AIC的值大于ARIMA（0， 1， 1）模型。故確認使用ARIMA（0， 1， 1）模型，為：

（1-B）xt=Θ（B）εt，

Θ（B）=1-0.3192B。

進行QQ檢驗，輸出結果為：X-squared = 8.9097，df=6，p-value=0.1787，模型的殘差沒有通過顯著性檢驗，認為殘差為白噪聲序列，ARIMA模型能較好地擬合本數(shù)據(jù)。

4.模型預測

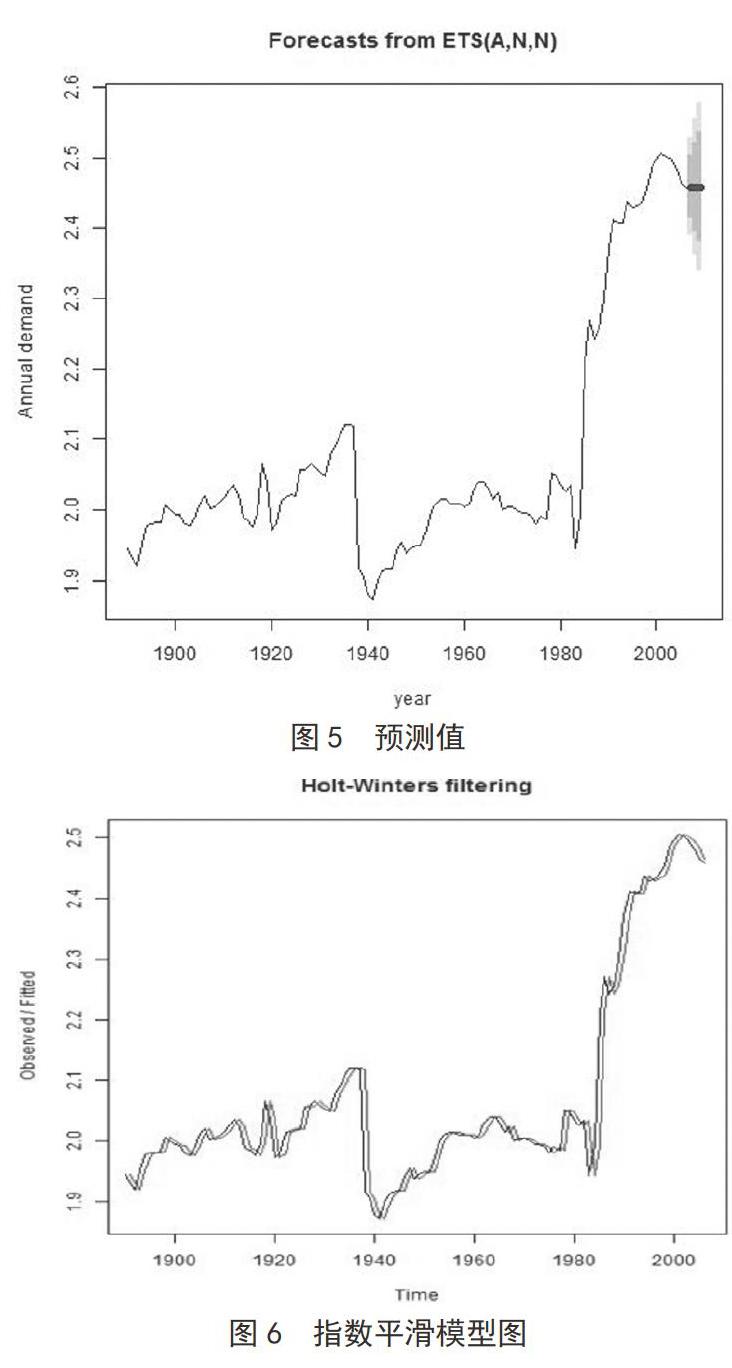
在模型擬合好并通過評價以后，就可以用來做預測。由于ARIMA模型只能用于短期預測，長期的預測是沒有意義的。故我們預測未來三年的值，得到的預測值2007年酒類產(chǎn)品人均需求量在（2.389372， 2.526629）

區(qū)間內，2008年， 為（2.360950， 2.555051） 區(qū)間內，2009年， 為（2.339141， 2.576860），見圖5。

5.模型進一步優(yōu)化

對于ARIMA模型，其擬合雖然契合度較高，但在進行預測時，實際上是對已經(jīng)差分過的平穩(wěn)序列進行的，所以其實際預測效果并不好。本文認為，酒類飲品存在著季節(jié)效應，例如：逢節(jié)假日、升學日或畢業(yè)季時，酒類飲品需求量較平時高，此時，可利用指數(shù)平滑法中的 Holt-Winters 三參數(shù)指數(shù)平滑模型進行預測。利用 R語言實現(xiàn) Holt-Winters 模型擬合以及預測，指數(shù)平滑模型圖如圖6，用這個模型在進行一次預測，如圖7。可以看出，原擬合效果還是比較好的，但其具有滯后性。

（二）結果分析

由上述模型求解過程我們可以得出人均酒類飲品的需求量的擬合模型為：由預測圖可以看出，在1980年后呈現(xiàn)出明顯的增長，21世紀以來一直處于較高的需求水平，預測結果顯示，未來三年仍然處于較高的需求狀態(tài)，根據(jù)時序圖的趨勢，我們可以認為，未來三年不會產(chǎn)生需求量的大幅下降或提升，人們雖有需求但并不急需。本文認為此時不應大幅提高酒類飲品的價格，可通過推出新產(chǎn)品等方式刺激消費。

參考文獻：

[1]Robert I.Kabacoff.R語言實戰(zhàn)（第二版）[M].人民郵電出版社，2016，5：337-339.

[2]王燕.應用時間序列分析（第四版）[M].中國人民大學出版社，2015，12：110-113.