雙基地角時變下的ISAR稀疏孔徑自聚焦成像
朱曉秀,胡文華,馬俊濤,郭寶鋒,薛東方
陸軍工程大學(石家莊校區) 電子與光學工程系,石家莊 050003
雙基地逆合成孔徑雷達(Inverse Synthetic Aperture Radar,ISAR)是發射站和接收站分開放置的ISAR系統[1-2],不僅能夠克服單基地ISAR成像中存在的幾何盲區問題,而且具有探測距離遠、隱身性能好、抗干擾能力強及獲取信息豐富等優勢,成為現代雷達技術研究熱點之一[3]。由于雙基地角的存在,其成像分辨率比相應的單基地雷達低,時變的雙基地角還容易引起越分辨單元徙動和圖像畸變等問題[4],影響成像質量。另外,在雷達成像時,通常需要不斷切換波束指向對多目標進行多視角觀測,對單個目標而言,其方位孔徑可能存在不連續性,當外界存在干擾導致某些回波數據誤差較大需要被剔除時,也會形成稀疏孔徑[5-8]。由于孔徑的缺失,經傳統的平動初補償后,回波數據中仍可能存在殘余的空變相位誤差,導致圖像散焦[9]。在雙基地角時變和稀疏孔徑的條件下,直接利用傳統的距離-多普勒(Range-Doppler, RD)算法會引起較高的旁瓣和能量泄漏,導致圖像散焦、分辨率低,因此有必要研究高分辨成像算法。
由于ISAR圖像有很強的空域稀疏性[10-11],不少學者將壓縮感知(Compressive Sensing,CS)理論[12]應用到ISAR成像中,實現了單基地ISAR高分辨成像。文獻[13]假設目標圖像各像元稀疏同分布,將ISAR圖像重構和相位誤差校正問題轉化為基于l1范數稀疏約束最優化問題,文獻[14]將該方法應用到稀疏孔徑當中,實現了ISAR稀疏孔徑自聚焦高分辨成像。文獻[15]假設像元稀疏非同分布,提出了一種基于加權l1范數稀疏約束最優化算法,能更好地實現目標圖像重構和相位自聚焦,提高了成像質量。但該類算法只利用了目標圖像的稀疏特性,有時候不能獲得最優稀疏解,且求解時涉及二維數據矢量化的操作,運算復雜度大。貝葉斯壓縮感知(Bayesian Compressive Sensing,BCS)[16]理論將貝葉斯推理與壓縮感知相結合,在利用目標圖像先驗信息的同時考慮了圖像的整體結構信息和噪聲統計信息,能夠求得更優的稀疏解。文獻[17]假設目標圖像服從Gaussian先驗建立稀疏先驗模型,利用貝葉斯推理進行求解,提出了基于稀疏貝葉斯學習(Sparse Bayesian Learning,SBL)的高分辨成像算法,相比于基于l1范數稀疏約束算法能進一步提高成像質量,文獻[18]在此基礎上,考慮了相位誤差,實現了自聚焦高分辨成像。但該類算法一般在實數域進行求解,在求解時需要先將復數回波信號轉為實數,增加了數據存儲量和運算復雜度。若雙基地角恒定,可將單基地中的成像算法直接應用到雙基地中,但雙基地角一般是時變的,存在一定的多普勒偏移可能引起越分辨單元徙動和圖像畸變等問題,影響成像質量。
綜上所述,在雙基地角時變以及方位向稀疏孔徑的情況下,雙基地ISAR成像存在圖像散焦、分辨率低等問題,相應的算法也存在稀疏效果不強、運算效率低等問題,基于此,本文提出了一種基于復BCS的雙基地ISAR稀疏孔徑自聚焦成像算法。該算法以平動補償后的二維數據為基礎,先構造補償相位將產生多普勒偏移的項補償掉,再根據變化的雙基地角和累積轉角構造稀疏基矩陣,將回波模型表示成符合CS理論的矩陣形式。在BCS理論中,Laplace先驗比Gaussian先驗具有更強的稀疏促進作用[19],所以本文假設目標圖像各像元服從復Laplace先驗建立稀疏先驗模型,將相位誤差作為模型誤差,利用貝葉斯推理通過迭代交替求得目標圖像和相位誤差,最后得到高精度的雙基地ISAR自聚焦圖像。求解時直接在復數域進行貝葉斯推理,通過“分布式”計算的方法將距離維和方位維進行分維處理,先逐距離單元處理實現目標圖像重構,再逐脈沖處理實現相位誤差更新,避免了將復數信號轉換為實數以及將二維矩陣矢量化處理,提高了運算效率。在不同相位誤差形式、不同孔徑缺失情況和不同信噪比(Signal to Noise Ratio,SNR)的條件下,仿真實驗驗證了算法的有效性和優越性。
1 雙基地ISAR成像模型
1.1 幾何模型
假設目標運動軌跡與收發雙站在同一平面上,建立雙基地ISAR成像幾何模型如圖1所示,發射站雷達為T,接收站雷達為R,基線長度為L,點E為等效單基地雷達位置。假設目標以速度V做勻速運動,成像起始時刻為t1,雙基地角為β1,以目標質心點O1為原點,雙基地角平分線方向為y1軸建立右手直角坐標系x1O1y1,散射點P1在x1O1y1坐標系中的坐標為(xP,yP),設O1P1長度為d,與x1軸夾角為α1,目標質心O1到發射站、接收站的距離分為記為Rt1、Rr1,散射點P1到發射站、接收站的距離分別記為RtP1、RrP1。在tm時刻,目標質心運動至Om點,此時的雙基地角為βm,等效單基地雷達視角變化為θm,可以看作是由坐標系x1O1y1旋轉得到坐標系xmOmym的旋轉角度。同樣以目標質心Om為原點,雙基地角平分線方向為ym軸建立右手直角坐標系xmOmym,散射點由P1運動至Pm,OmPm與xm軸夾角為αm且αm=θm+α1,目標質心Om到發射站、接收站的距離分別記為Rtm、Rrm,散射點Pm到發射站、接收站的距離分別記為RtPm、RrPm。
圖1 雙基地ISAR成像幾何模型Fig.1 Geometry model of bistatic ISAR imaging
1.2 信號模型
假設發射站雷達以脈沖重復周期Tr發射線性調頻信號
(1)
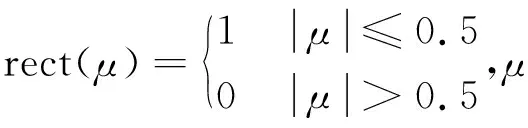
(2)
式中:c為光速。
(3)
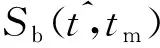
(4)
式中:ΔRPm為散射點到收發雙站的距離與目標質心到收發雙站的距離之差,表示為
(5)
假設在觀測范圍內累積轉角變化很小,可近似為:sinθ(tm)≈θ(tm),cosθ(tm)≈1,將式(5)代入式(4),則一維距離像可近似為
(6)
1.3 多普勒偏移相位補償
(7)
由式(7)可知,最后近似結果中的第一項與xP有關,用于提取散射點的多普勒信息,進行方位向高分辨,第二項與yP有關,將會引起圖像畸變,且畸變量與距離坐標成正比,也有可能引起多普勒徙動,由于該項是由式(6)相位中的第二項引起的,因此先構造相應的補償相位將該項補償掉,構造的補償項為
(8)
則相位補償后的一維距離像為
(9)
2 基于CS的自聚焦成像模型
2.1 稀疏基矩陣的構造
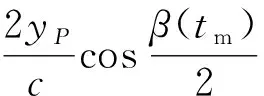
(10)
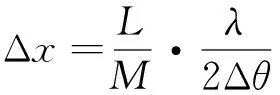
(11)
由于收發雙站的位置是固定已知的,即雙基地基線距離已知,并且雷達都具有測距功能,相當于各脈沖時刻目標到收發雙站的距離也是已知的,雙基地角就可以利用簡單的三角幾何關系計算出來,并且測距精度對稀疏矩陣的影響很小。因此,可將稀疏基矩陣Fall構造為
(12)
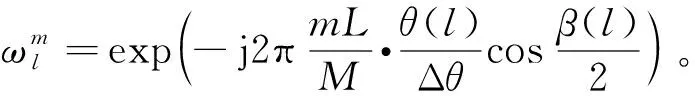
2.2 雙基地ISAR回波的稀疏表示
考慮到實際有噪聲的存在,將式(10)的回波數據用矩陣形式表示為
Sall=FallA+ε0
(13)
式中:Sall表示經過運動補償和相位補償后的全孔徑二維回波數據,共包含L個回波脈沖,N個距離單元;ε0為L×N維噪聲矩陣;Fall表示L×M維的橫向稀疏基矩陣,當M=L時,可得到高分辨ISAR圖像,當M>L時,算法可以實現超分辨,超分辨倍數為M/L;A表示需要求解的ISAR超分辨二維圖像,每一個元素對應散射點的復幅度。
2.3 稀疏孔徑條件下的自聚焦成像模型
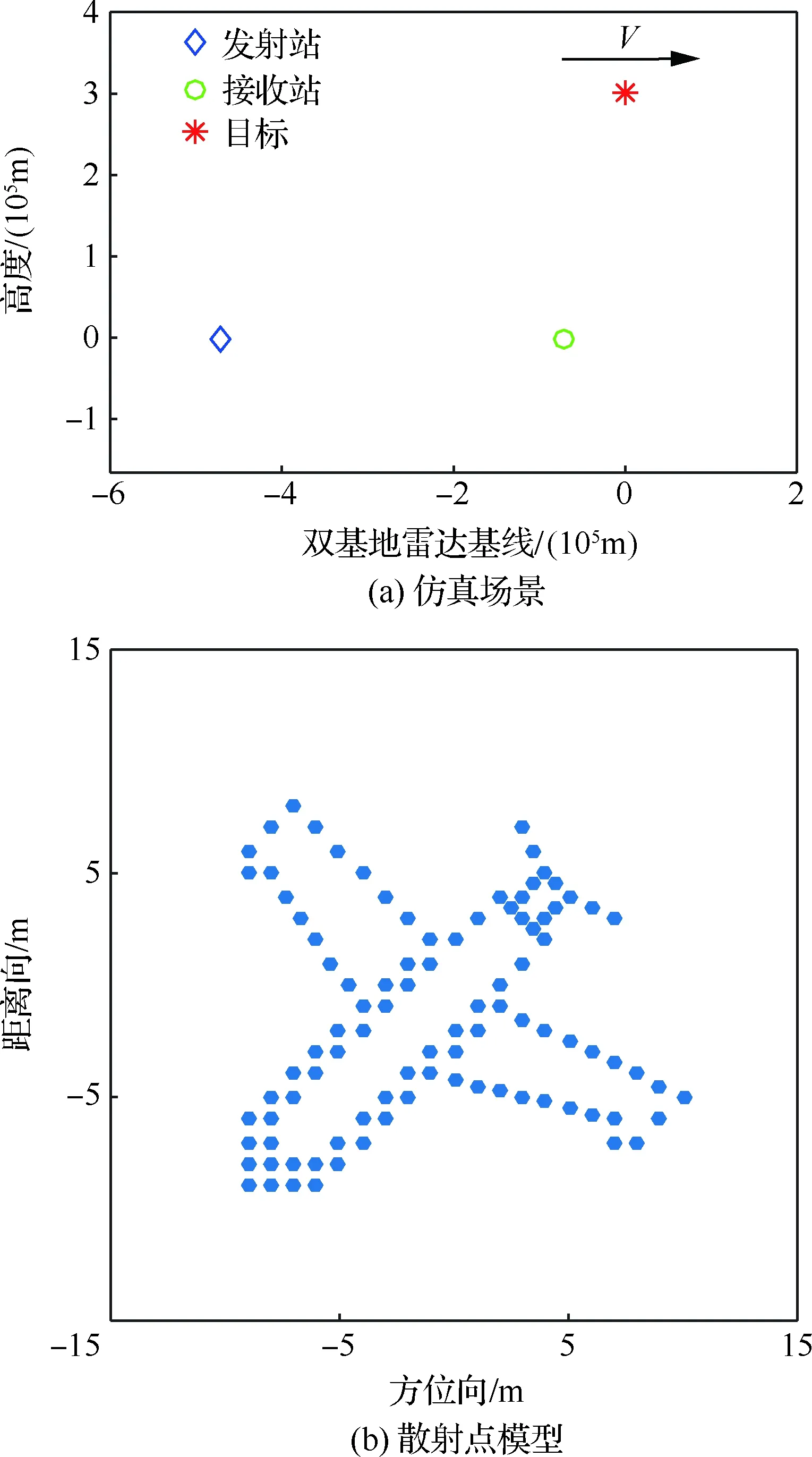
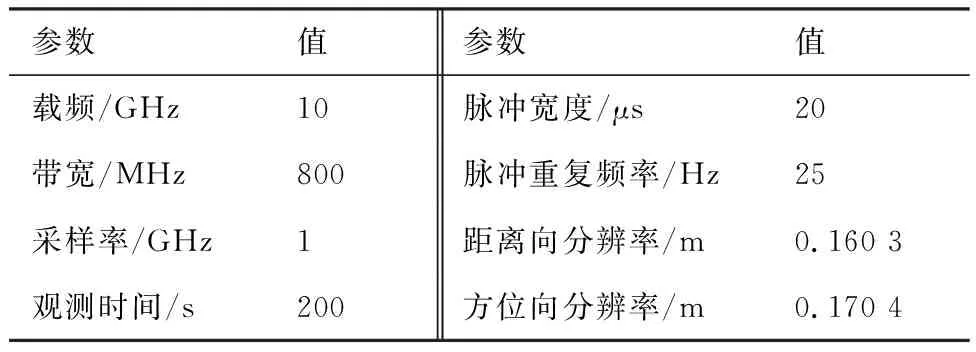
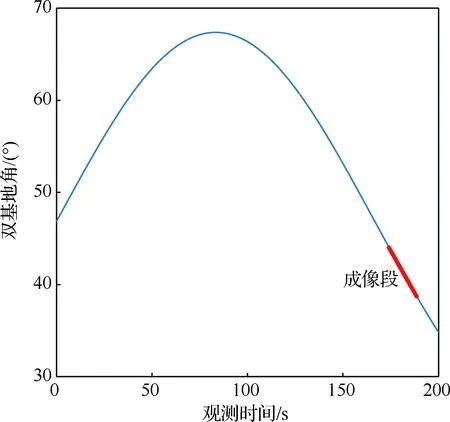
在稀疏孔徑的情況下,數據可能存在隨機缺失和塊缺失兩種缺失形式,其稀疏孔徑模型示意圖如圖2所示,其中黑色表示缺失孔徑數據,白色表示有效孔徑數據。假設S為融合的有效孔徑回波數據,共包含K(K SK×N=TK×LSall=TFallA+ε=FA+ε (14) 式中:T為有效數據選擇矩陣,具有去除缺失孔徑、合并有效孔徑的作用;F為在稀疏基矩陣Fall中去除缺失孔徑對應行后形成的K×M維部分稀疏基矩陣;ε為K×N維復噪聲矩陣。 圖2 兩種稀疏孔徑模型Fig.2 Two models of sparse aperture 假設ISAR回波信號經距離維脈沖壓縮之后,已經做過包絡對齊和相位校正的平動初補償處理,但由于孔徑缺失導致在傳統的相位校正方法后仍可能存在殘余的空變相位誤差,影響方位向成像處理。因此,考慮到相位誤差的存在,可將式(14)改寫為 S=EFA+ε (15) 式中:E=[diag(ejφ1,ejφ2,…,ejφK)]K×K為相位誤差矩陣,φk為第k個回波包含的殘余相位。 在BCS框架下的稀疏信號恢復算法一般假設涉及的數據為實數,但在雷達成像時,回波信號為復數,簡單的解決算法是將復數信號分解為實部和虛部兩部分,即把復數表達式轉換為實數形式,但這樣不僅會增加數據的存儲量和計算量,而且該算法將信號的實部和虛部視為兩個獨立的分量,對它們分別進行稀疏估計,由于重構過程相互獨立,存在的估計誤差必然會影響復數相位,進而影響后續的相位自聚焦過程,所以算法性能還有待提升。因此,本文研究了一種直接在復數域處理的基于BCS的雙基地ISAR稀疏孔徑自聚焦成像算法,對實部和虛部采用了相同的權約束,即直接對該復數像元的模進行約束,因此在重構過程中可以保留像元的相位關系,更有利于算法的自聚焦過程,與傳統的算法相比,不僅降低了計算量,而且還可以提高重構性能。 3.1.1 噪聲統計模型 假設ε是復高斯白噪聲,其虛部和實部分別獨立服從方差為σ2的實高斯分布,則回波信號的似然函數為 P(S|A,σ2)= (16) 對σ-2再施加Gamma先驗,利用超參數進行約束,即 p(σ-2)=Gamma(σ-2|c,d) (17) 3.1.2 目標圖像稀疏先驗模型 (18) 式中:αij≥0、λ≥0。為限制超參數λ的取值范圍,引入超參數ξ對λ施加Gamma先驗分布: p(λ|ξ)=Γ(λ|ξ/2,ξ/2) (19) 因此,通過式(18)和式(19)可知,Laplace先驗實際上等價于三層貝葉斯概率模型,即通過ξ→λ→αij→aij依次實現對像元aij的稀疏先驗,不同的像元使用不同的α體現一種獨立約束關系,而所有α都服從相同指數分布。 為方便求解,只考慮某一特定距離單元數據S·n,則式(15)可表示為 EHS·n=FA·n+ε·n (20) 式中:EHS·n表示相位誤差補償后的回波數據。若超參數αn、λ、σ2已知,則利用噪聲和目標圖像的稀疏先驗信息,根據貝葉斯準則,p(A·n|EHS·n,αn,λ,σ2)可看做是服從均值為μn、協方差為Σn-λ的復高斯分布[19],且 μn=σ-2Σn-λFHEHS·n (21) Σn-λ=(σ-2FHF+Λn)-1 (22) 要得到重構的目標圖像,就必須先進行超參數αn、λ、σ2的求解。由于p(αn,λ,σ2|EHS·n)=p(α,λ,σ2,EHS·n)/p(EHS·n),故p(αn,λ,σ2|EHS·n)∝p(α,λ,σ2,EHS·n),通過最大化聯合分布p(α,λ,σ2,EHS·n)就可估計出超參數αn,λ,σ2。根據貝葉斯準則,有 p(α,λ,σ2,EHS·n)= p(α|λ)p(λ)p(σ2)dA·n= p(α|λ)p(λ)p(σ2) (23) L=lgp(α,λ,σ2,EHS·n)= (24) 利用求導的方式求解超參數,即利用式(24)分別對lgαin、σ-2和λ求偏導等于零且取正值,可 得到超參數αin、σ2和λ的更新公式為 (25) (26) (27) 為計算簡便,令ξ→0[19],將式(27)代入式(25) 可得 (28) (29) (30) (31) (32) 假設原始回波數據經過了脈沖壓縮處理,并做包絡對齊和初相校正后得到了一維距離像,在此基礎上利用所提算法僅在方位向實現稀疏孔徑重構成像。根據式(32),要實現相位自聚焦,就需要在每次迭代中利用所有距離單元的回波數據,因此每次迭代時必須得到整個二維像的結果。傳統的求解算法通常采用矩陣矢量化的操作[14],即將二維回波數據逐距離單元拉直為一維矢量,則式(15)可表示為 (33) 步驟1雙基地ISAR原始回波經脈沖壓縮,并做包絡對齊和初相校正后得到一維距離像,為解決雙基地角時變帶來的多普勒頻移問題,構造補償相位,得到補償后的二維回波數據Sall。 步驟2利用數據選擇矩陣T,去除缺失孔徑,合并有效孔徑,得到包含殘余相位誤差的方位向稀疏孔徑二維回波數據S。 步驟3構造稀疏基矩陣F,初始化超參數αin=1,σ2=0.01,初始化E=IK,g=1,設定總迭代次數G和門限eps。 步驟4進行相位誤差補償,得到補償后的回波數據Scom=EHS。 步驟6重構的目標圖像為 利用本文算法逐距離單元進行目標圖像重構時,對于某一距離單元,F是K×M維矩陣,Λn和Σn-λ是M×M維矩陣,EH是K×K維矩陣,S·n是K×1維矩陣,根據式(21)和式(22),則σ-2FHF的計算量為O(KM2),Σn-λFHEHS·n的計算量為O(KM2+MK2+MK),所以更新Σn-λ的計算量為O(M3+KM2),更新μn的計算量為O(KM2+MK2+MK),則本文算法一次迭代中處理N個距離單元實現目標圖像重構的總計算量為O(NM3+2NKM2+NMK2+NMK),相比于傳統算法的O(N2(NM3+2NKM2+NMK2+MK))要小很多,可有效提高運算效率。 本文仿真實驗環境為Windows 7 64位操作系統,MATLAB2016A軟件平臺,仿真所用計算機主要參數為:處理器為Intel酷睿i5-6200U,主頻為2.30 GHz,內存為4 GB。本部分通過仿真實驗從不同的相位誤差形式、回波SNR和孔徑缺失情形這3個方面對本文算法性能進行驗證。為方便直觀比較算法性能,采用目標背景比(Target-to-Background Ratio,TBR)和圖像熵En作為衡量標準,其定義可表示為 雙基地ISAR仿真場景如圖3(a)所示,目標的散射點模型如圖3(b)所示,該模型由96個散射點組成,成像的仿真參數設置如表1所示。假設雙基地基線長度為400 km,目標在300 km的高度以3 km/s的速度從水平距離距發射站雷達靠左50 km處開始勻速向右運動,假設總觀測時間為200 s,觀測時間內雙基地角變化曲線如圖4所示。從圖中可以看出,在觀測時間內,只有一部分時間內雙基地角變化較小,大多數情況下雙基地角變化較大。為體現雙基地ISAR成像過程中雙基地角的時變特性,以水平距離距接收站雷達靠右70 km處為成像起點,截取400個脈沖回波數據為成像段數據,如圖4中粗線段所示,該觀測時間內累積轉角約為5.39°,平均雙基地角約為41.38°。考慮成像段結束時刻,此時對應的雙基地角為38.46°,累積轉角為5.39°,載頻fc為10 GHz,yP取最大值9 m,由于誤差相位數量級要求一般與λ/8相比擬,根據式(8),若考慮補償的相位誤差在λ/8范圍內,則計算出雙基角范圍可在(38.38°,38.54°)內,即雙基地角誤差為Δβ=±0.08°,此時利用雷達雙站與目標的三角關系可以計算出允許的測距誤差范圍約為Δx=±3.02 m,雷達測距精度能夠滿足該要求。 圖3 仿真場景和散射點模型Fig.3 Simulation scene and scattering point model 表1 成像參數設置Table 1 Imaging parameters setting 圖4 雙基地角變化曲線Fig.4 Variation curve of bistatic angle 在全孔徑條件下,通過對預處理(包絡對齊和初相校正)后的回波添加不同形式的相位誤差,在低SNR條件下驗證算法的自聚焦性能。不同形式的相位誤差可能會影響算法迭代的收斂性,進而影響成像結果,特別是低SNR條件下對算法性能要求比較高,否則無法得到良好的聚焦圖像。因此,有必要在不同的相位誤差條件下進行仿真實驗,驗證算法的有效性。 在本實驗中,為回波數據添加3種不同形式的相位誤差,以驗證不同運動形式下的算法性能。① 二次相位誤差,主要用于分析由高速運動引起的相位誤差時算法的性能;② 正余弦相位誤差,主要用于分析由復雜運動引起的相位誤差時算法的性能;③ 隨機相位誤差,主要用于分析在由外界干擾或其他不定因素引起的相位誤差時算法的性能。為進一步驗證算法在低SNR條件下的成像性能,設置SNR為5 dB,比較算法在3種不同的相位誤差形式下的自聚焦性能。應用本文算法進行自聚焦成像時,總迭代次數設為20。添加的相位誤差形式及其成像結果如圖5所示,其中,圖5(a)~圖5(c)表示二次相位誤差及利用相位梯度自聚焦(Phase Gradient Autofocus,PGA)算法后直接FFT成像結果和本文算法的成像結果,圖5(d)~圖5(f)表示二次正余弦相位誤差及利用PGA算法和本文算法的自聚焦成像結果,圖5(g)~圖5(i)表示隨機相位誤差及利用PGA算法和本文算法的自聚焦成像結果。從圖中可以看出,在3種 不同形式的相位誤差條件下,PGA算法雖有一定的自聚焦效果,但低SNR條件下對噪聲的抑制效果不強,存在的噪點嚴重影響了成像質量,而本文算法不僅具有良好的聚焦性能,而且能夠很好地抑制噪聲,得到較好的自聚焦成像效果,說明該算法的適用性和魯棒性較強,可在低SNR的情況應用,且應用時不用考慮相位誤差的具體形式。 圖5 不同相位誤差形式及其成像結果Fig.5 Different phase error forms and imaging results 另外,從表2的成像衡量指標中還可看出,本文算法所得圖像的TBR值在二次相位誤差條件下最大,隨機相位誤差條件下最小,熵值則相反,說明本文算法雖在3種不同相位誤差形式下均能較好地實現自聚焦,但隨機相位誤差對算法性能要求略高于其他2種誤差。 表2 不同相位誤差形式下的算法成像指標對比 在稀疏孔徑條件下,通過改變孔徑缺失情形,將本文算法與基于l1范數稀疏約束的自聚焦算法和基于SBL的自聚焦算法的成像結果進行對比,驗證算法在稀疏孔徑條件下的有效性和優越性。本實驗主要研究孔徑缺失較多的4種缺失情形下的成像結果,在SNR為10 dB下,為回波數據添加幅度浮動在-π~π的隨機相位誤差,4種缺失情形分別是50%數據隨機缺失、75%數據隨機缺失、50%數據塊缺失和75%數據塊缺失,孔徑缺失位置和對應的RD算法成像結果如圖6所示。3種 不同的高分辨算法下的成像結果如圖7所示,其中,圖7(a)~圖7(c)為50%數據隨機缺失時3種算法的成像結果,圖7(d)~圖7(f)為75%數據隨機缺失時3種算法的成像結果,圖7(g)~圖7(i) 為50%數據塊缺失時3種算法的成像結果,圖7(j)~圖7(l)為75%數據塊缺失時3種算法的成像結果,具體的評價指標數據如表3所示。在添加的隨機誤差范圍為-π~π時,從成像結果可以看出,當數據缺失率為50%時,3種算法都能重構出目標圖像輪廓,但基于l1范數稀疏約束算法將會丟失目標的一些細節信息,基于SBL算法存在一些虛假點影響成像質量,而本文算法能夠得到清晰的目標圖像。隨著孔徑缺失數據增加,特別是當缺失孔徑數為全孔徑的75%時,基于SBL算法成像質量迅速下降,與基于l1范數稀疏約束算法所恢復出的目標圖像輪廓不清晰,有散射點缺失、出現虛假散射點和噪聲抑制效果差的現象存在,自聚焦效果有所下降,但本文算法仍能重構出清晰的高質量目標圖像。從表3中的數據還可以看出,在同一孔徑缺失條件下,本文算法所得圖像的熵值最小,TBR值最大,而基于l1范數稀疏約束算法所得圖像的熵值最大,TBR值最小,這也說明了本文算法成像效果最好,其次是基于SBL算法,基于l1范數稀疏約束算法相比來說成像質量較差。另外,在同樣多的有效數據情況下,可以看出數據隨機缺失比塊缺失時成像質量要好,這是由于數據塊缺失所破壞的回波信號之間的相干性更大,導致恢復起來比較困難。在塊缺失數據為75%時,本文算法與其他2種算法相比仍能較好地恢復出目標圖像,說明了本文算法的優越性。 圖6 4種孔徑缺失情況及其RD成像結果Fig.6 Four sparse aperture cases and RD imaging results 圖7 4種孔徑缺失情況下3種算法成像結果Fig.7 Results of imaging with three algorithms in four sparse aperture cases 表3 不同孔徑缺失情況下的算法成像指標對比 為驗證算法在不同SNR條件下的成像性能,在方位向數據隨機缺失比為50%的情況下,利用基于l1范數稀疏約束的自聚焦算法、基于SBL的自聚焦算法和本文算法在不同SNR條件下進行稀疏孔徑成像,并畫出重構圖像的圖像熵和TBR隨SNR的變化曲線,如圖8所示。從變化曲線圖可以看出,在同一SNR條件下,相較于其他2種算法,利用本文算法所得圖像的熵值最小、TBR值最大,說明本文算法比其他2種算法的成像質量要好。另外,隨著SNR降低,雖然3種算法的成像結果的熵值都有所增大、TBR值有所減小,但本文算法變化較小,說明SNR對本文算法的影響較小,即本文算法在低SNR條件下仍然適用。 圖8 成像質量隨SNR變化曲線Fig.8 Curves of variation of imaging quality with SNR 1) 構造了元素隨雙基地角和累積轉角變化的稀疏基矩陣,更符合信號特性,有利于信號重構。 2) 直接在復數域進行基于Laplace先驗的貝葉斯推理,不僅減少了運算量,而且保留了復數信號的相位關系,有利于提高算法的相位自聚焦性能。 3) 采用“分布式”計算方法先逐距離單元再逐脈沖進行求解,實現目標重構和相位自聚焦,避免了傳統求解方法中將二維矩陣矢量化處理所帶來的運算復雜度高和數據存儲量大的問題,提高了運算效率。 但是,論文未考慮目標軌跡與雷達站不共面的情況,在這種情況下算法能否依然適用以及適用的邊界條件還需要進一步研究。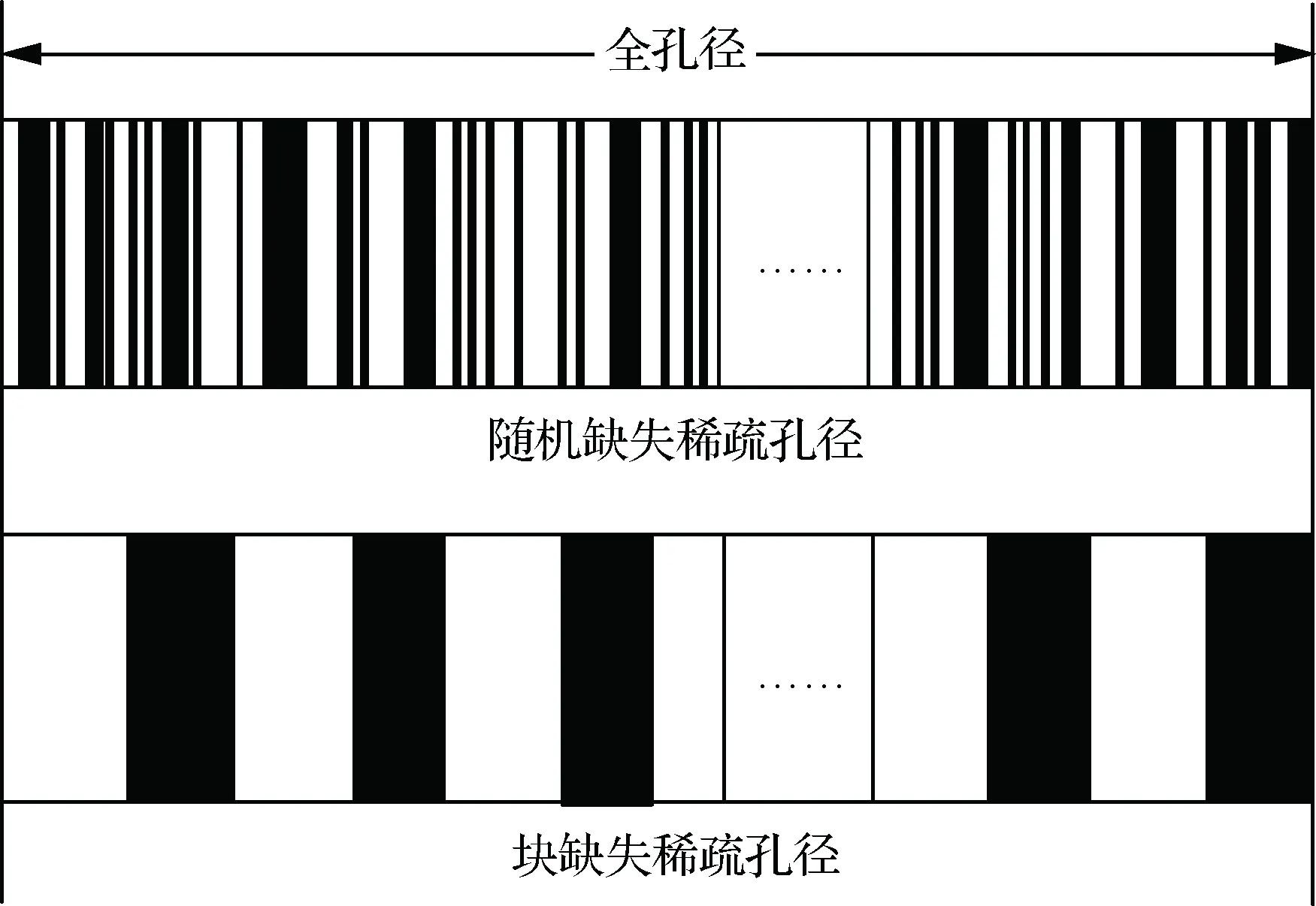
3 基于Laplace先驗的復BCS求解
3.1 目標圖像超參數模型


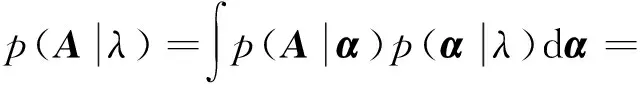
3.2 目標圖像重構
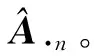
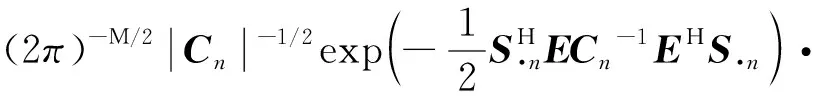
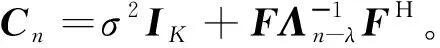
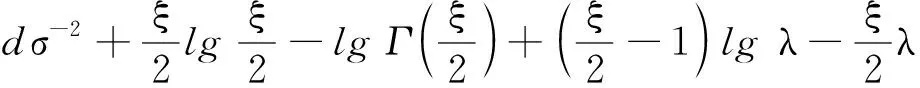
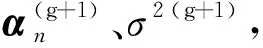

3.3 相位誤差更新補償
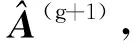
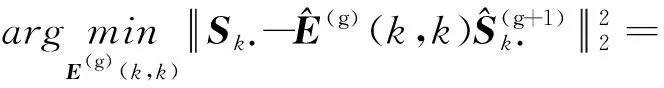
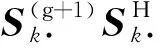
4 成像算法流程
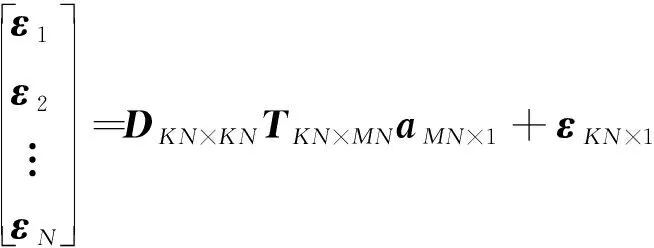
5 仿真實驗與分析
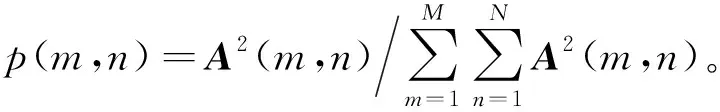
5.1 仿真場景和參數設置
5.2 不同相位誤差形式下性能驗證
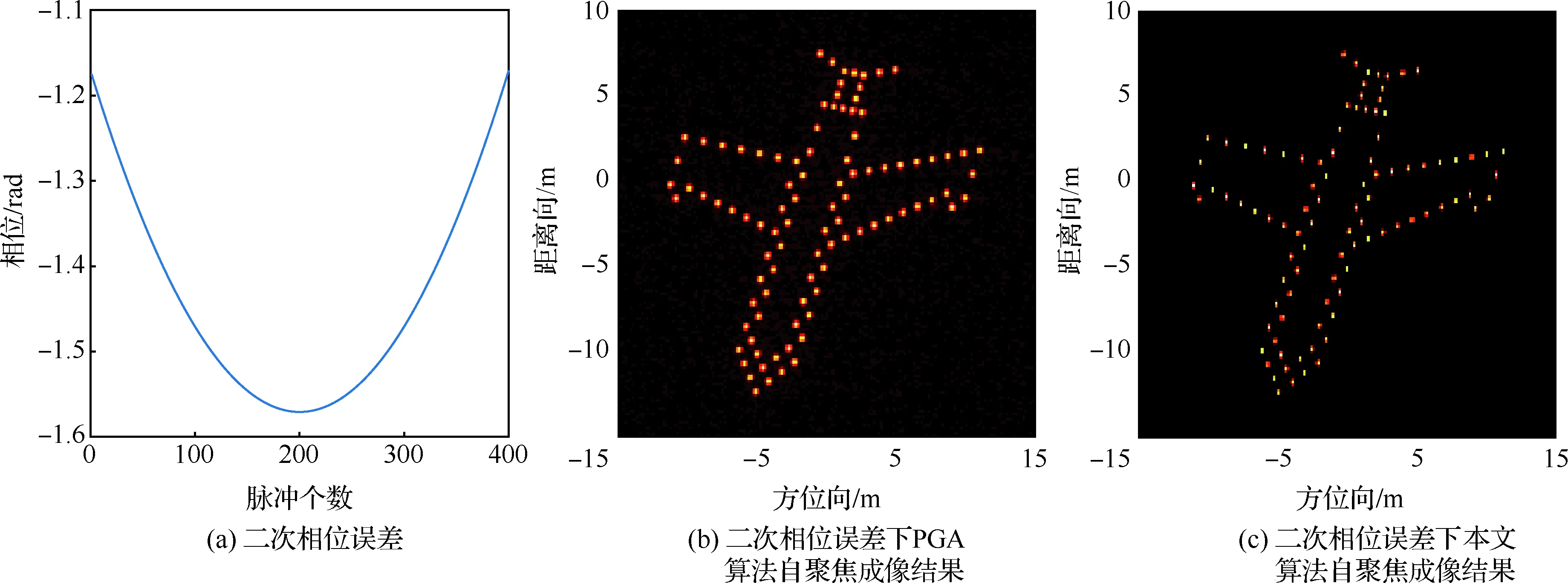
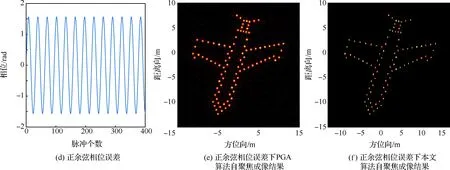
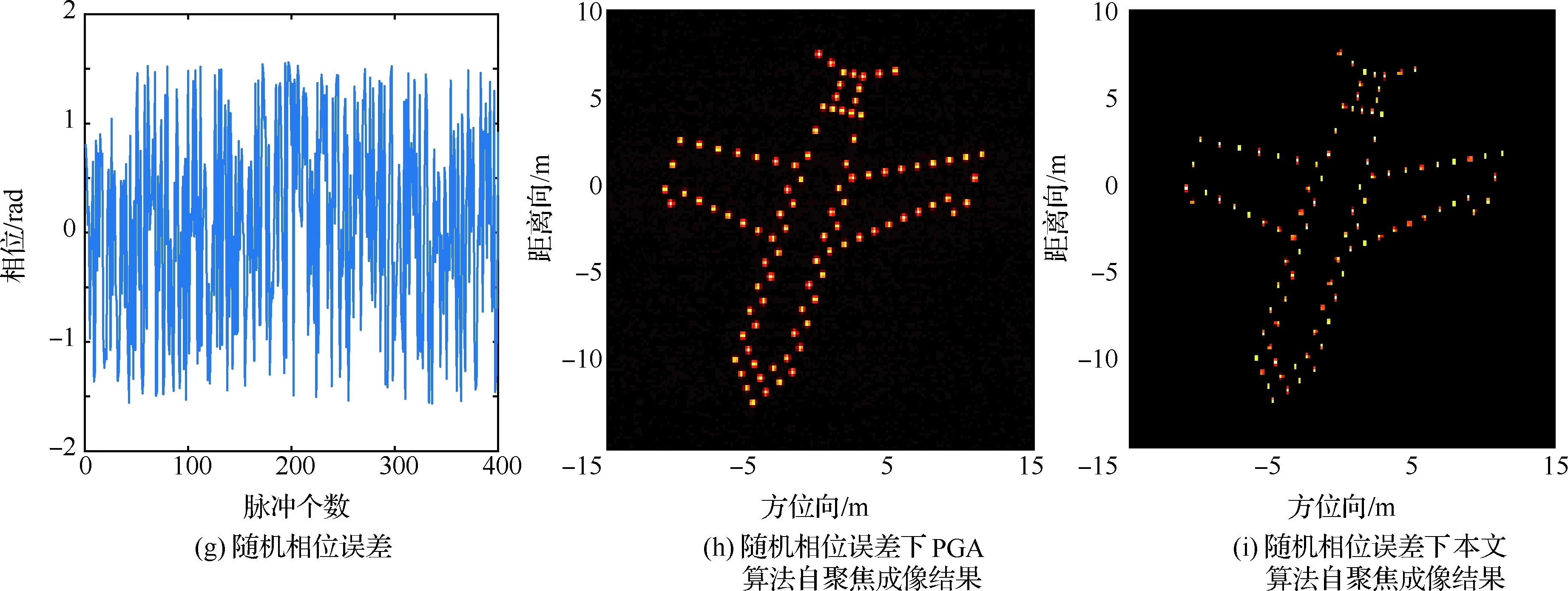
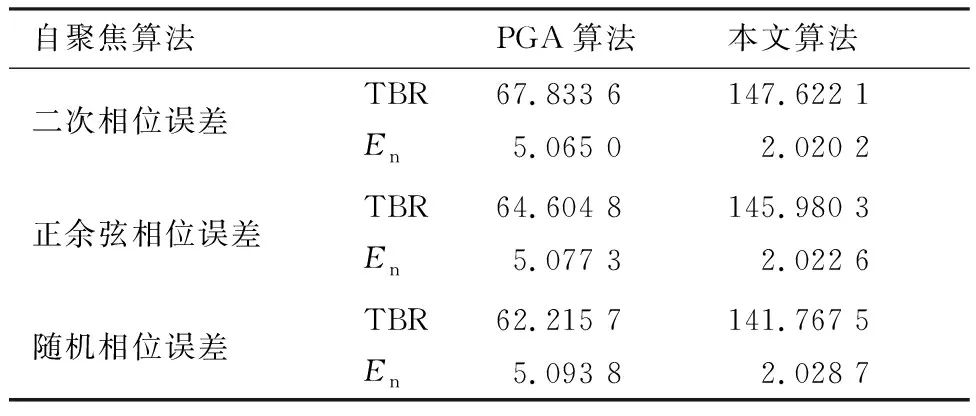
5.3 不同孔徑缺失情形下算法性能驗證
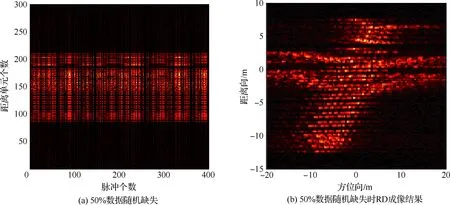
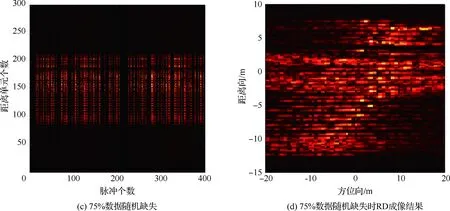
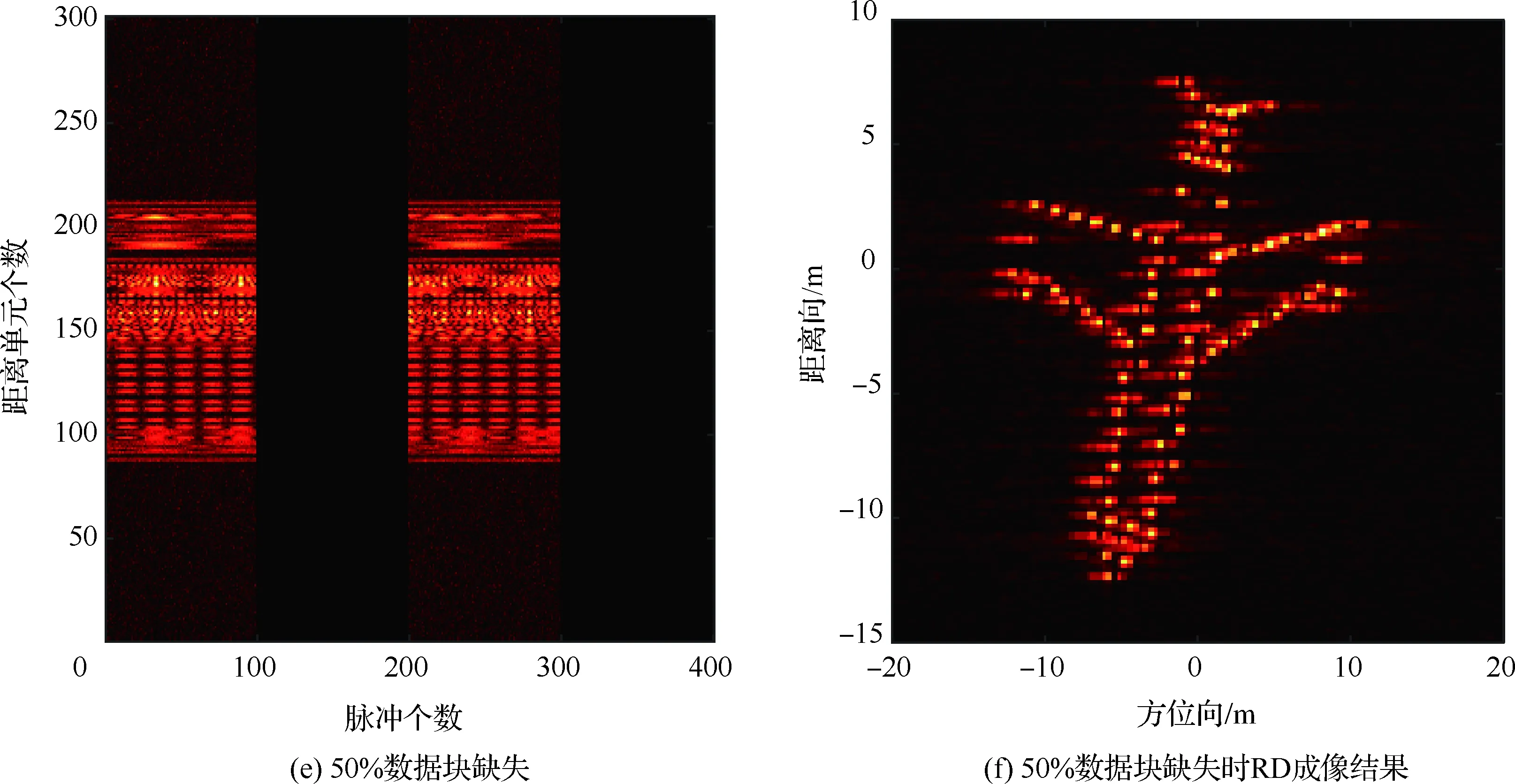

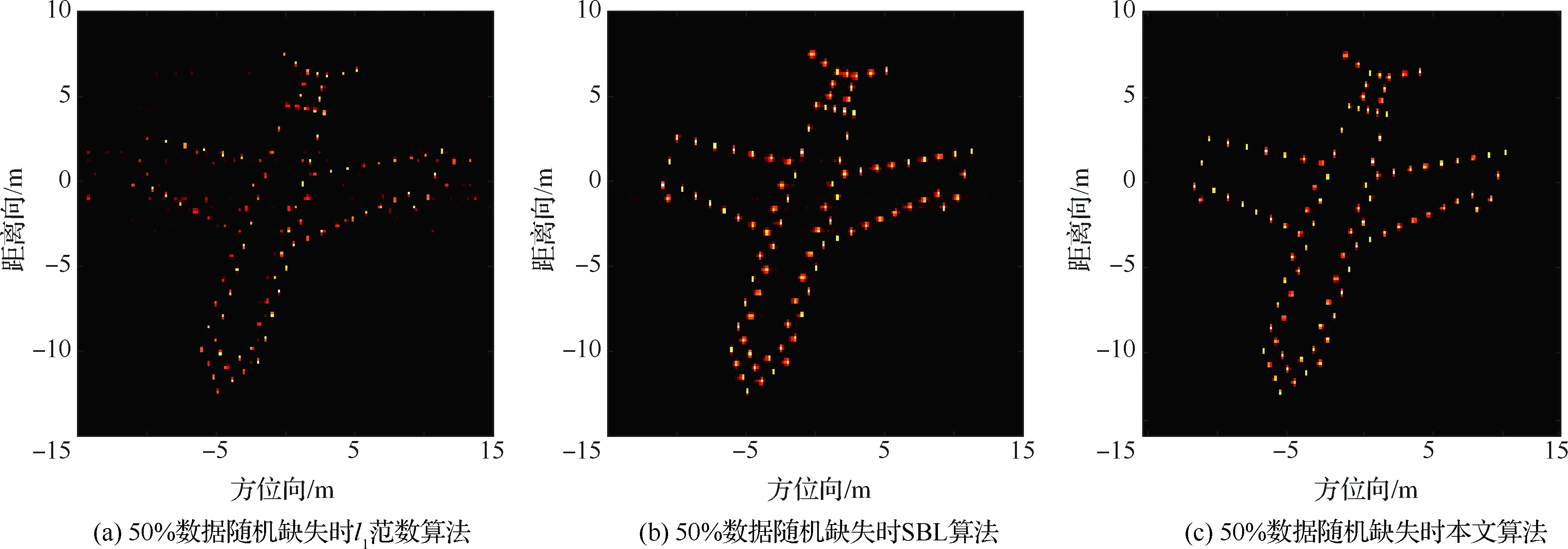
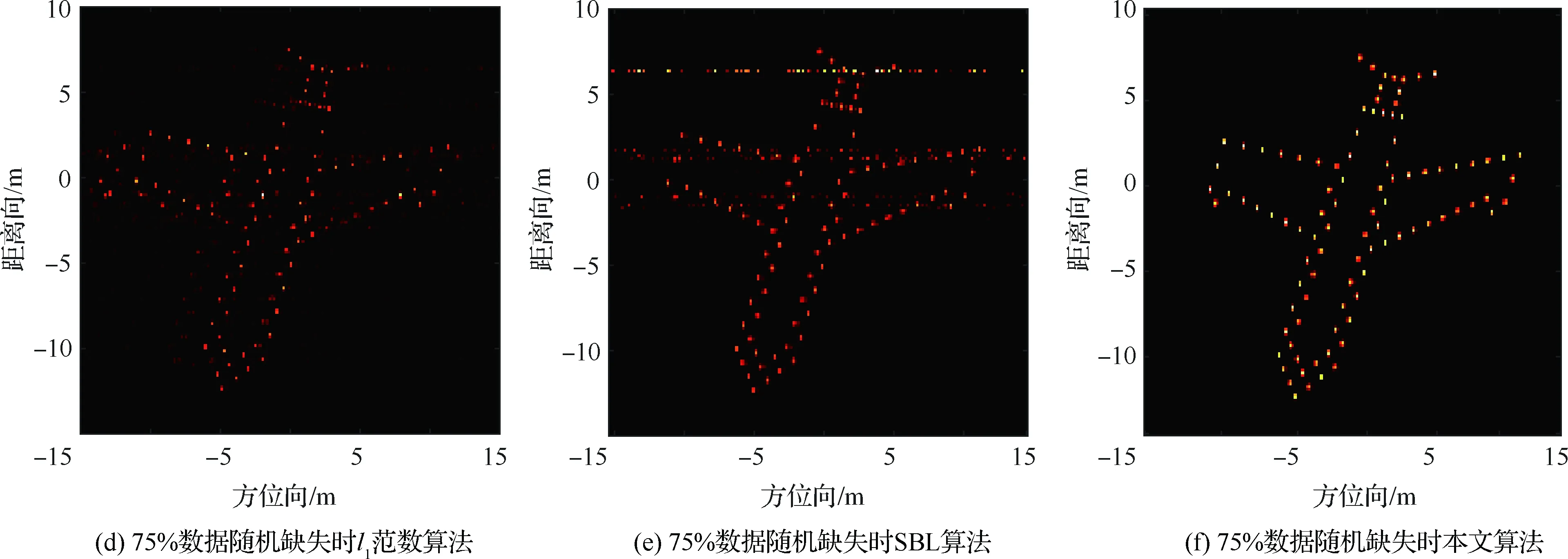
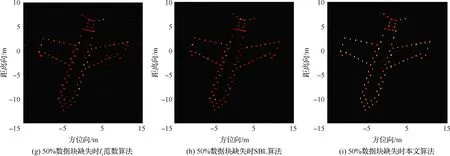
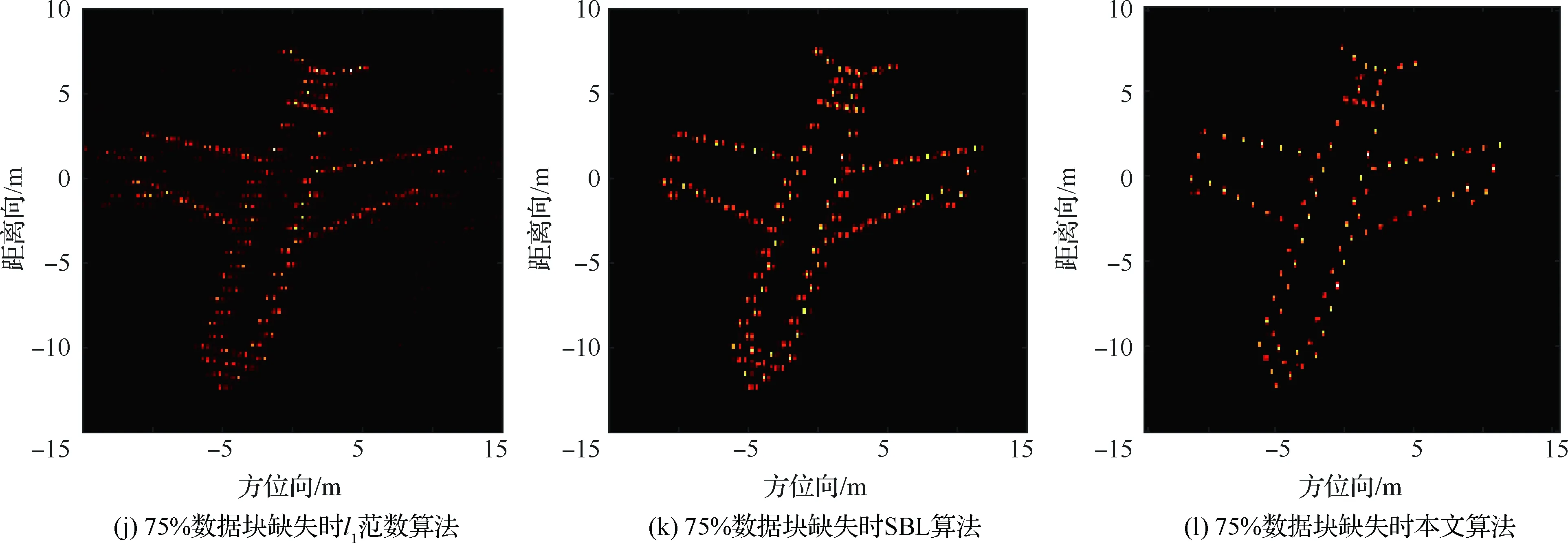
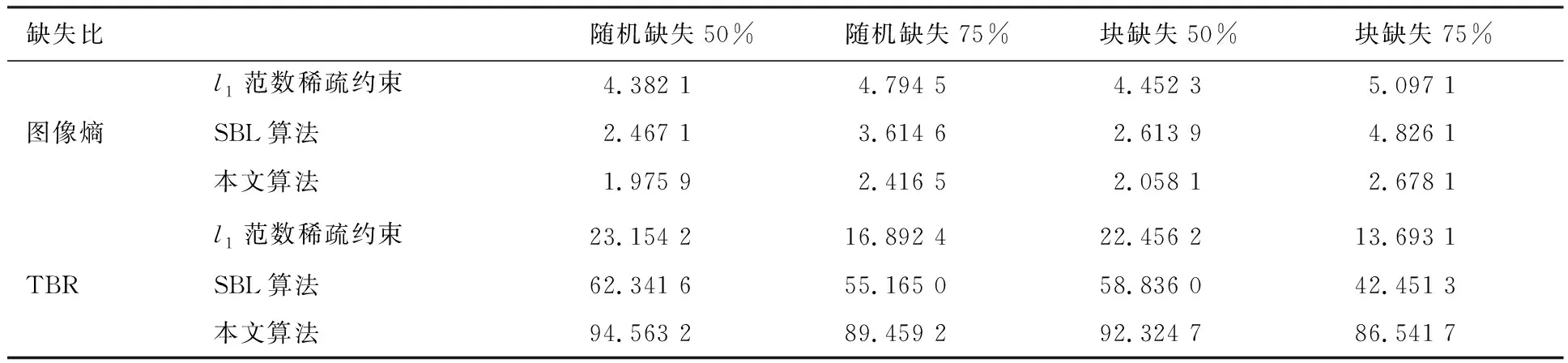
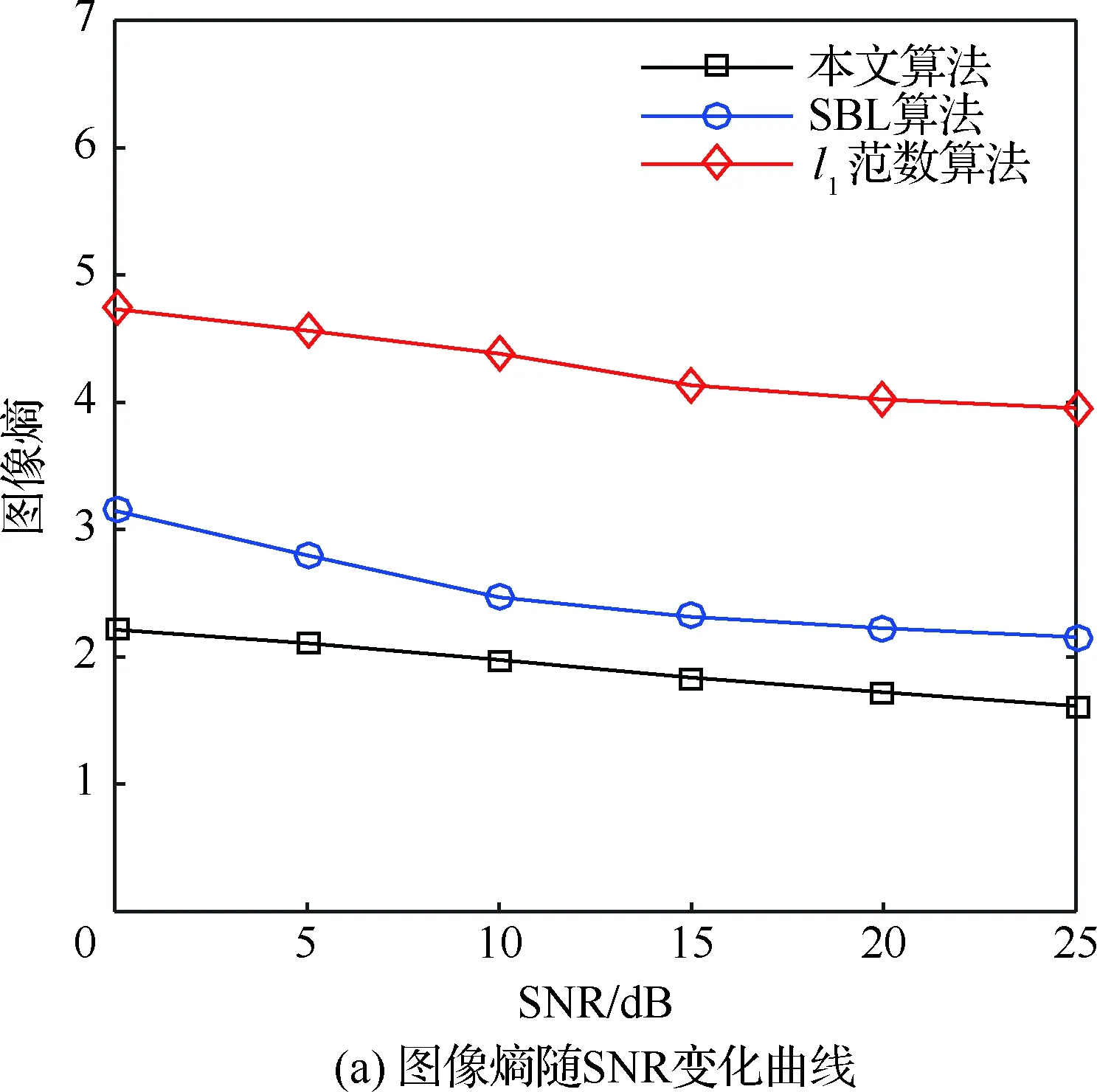
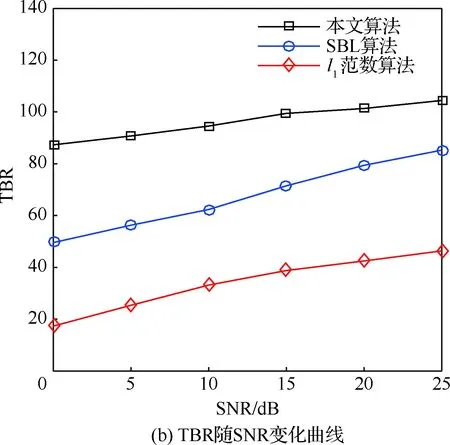
5.4 不同SNR條件下算法性能驗證
6 結 論

