帶異步相關噪聲的戰斗機蛇形機動跟蹤算法
盧春光,周中良,劉宏強,寇添,楊遠志
空軍工程大學 航空工程學院,西安 710038
蛇形機動是戰斗機飛行員在隱蔽接敵、機動規避及協同探測等戰術動作中經常采用的戰術機動類型。在一定的空戰態勢下,飛行員進行蛇形機動反映了其戰術意圖,因此在空戰中如何快速而又準確地識別出目標的蛇形機動模式對于明確其戰術意圖以及評估當前的戰場態勢具有十分重要的意義。目前,機動模式的識別主要從機動模式的幾何特征(宏觀)以及運動參量特征(微觀)兩個方面著手:文獻[1]通過將戰術機動進行分割并按時間序列進行編碼,采用隱馬爾科夫模型進行訓練、識別;文獻[2]通過提取目標航向角變化率、高度變化率等運動參量特征,設計了一個兩級識別方案,采用模糊推理和時間自動機方法實現了機動模式的識別。對于蛇形機動目標而言,轉彎角速度是其最為關鍵的運動參量,因此通過載機雷達的量測數據精確辨識出轉彎角速度對于提高戰斗機蛇形機動模式的識別率具有重要意義。
目前,機動目標轉彎角速度辨識的問題已經得到了許多學者的關注。Roth[3]、Arasaratnam[4]、Jia等[5]、Huang[6]等將轉彎角速度作為額外的狀態變量,從而對狀態進行擴維處理,分別使用擴展卡爾曼濾波/無跡卡爾曼濾波、容積卡爾曼濾波、基于5階球徑容積規則的高階容積卡爾曼濾波、高階魯棒容積卡爾曼濾波等非線性濾波方法辨識角速度和估計狀態變量。缺點是角速度估計的精度依賴于目標初始狀態及協方差、過程噪聲和量測噪聲等因素;黃偉平等[7]、Zhu和Cheng[8]、Efe和Atherton[9]分別根據轉彎角速度與目標速度方向角、速度、加速度之間的物理關系,首先采用非線性濾波算法估計出目標速度方向角、速度、加速度等狀態量,而后間接辨識出轉彎角速度。Yuan等[10]通過引入距離變化率量測,采用Cmin方法[11]并結合航向角的變化估計出兩個可能的轉彎角速度的值,基于此設計包含勻速模型和兩個勻速轉彎模型的交互多模型算法進行狀態估計。Frencl等[12]通過引入距離變化率量測估計轉彎角速度,并根據速度矢量在距離方向上的投影與距離變化率估計量之間的差異,對轉彎角速度進行進一步修正以提高估計精度,然后依據最優線性無偏估計準則,利用粒子濾波進行狀態估計。缺點是沒有考慮角速度與目標狀態之間相互耦合關系,增大了辨識風險;Bar等[13]通過采用勻速模型和擴維的勻速轉彎模型設計了交互多模型算法,用于估計轉彎角速度。缺點是辨識與估計精度依賴于模型切換概率與轉移概率的設置;Yuan等[14]提出了基于期望最大化(EM)算法的轉彎角速度辨識算法,該算法采取的是“先辨識-后估計”的策略,通過辨識出的轉彎角速度進而估計目標的運動狀態,缺點是依賴于初始值以及機動初始概率的設置。
在實際空戰中,非合作目標的轉彎角速度是未知且時變的,并且與目標狀態相互耦合、彼此影響,一方面目標狀態估計性能的提升有利于轉彎角速度的辨識,另一方面轉彎角速度辨識性能的提升有利于目標狀態估計精度的提高。上述文獻中所提到的轉彎角速度辨識方法均沒有考慮轉彎角速度與目標狀態之間的耦合關系以及這種耦合關系所帶來的影響,并且均采取的是開環序貫處理方式,沒有形成閉環反饋。而且上述文獻所提到的狀態估計與轉彎角速度辨識方法中,都需要假設量測噪聲與過程噪聲是相互獨立的,但是在實際跟蹤過程中,這種假設條件往往難以滿足,比如雷達在跟蹤目標時,受目標運動速度以及觀測角度的影響,導致過程噪聲與量測噪聲之間的相關性不能被忽略[15-16];在異步多傳感器信息融合過程中,由于量測值作為輸出反饋傳遞給網絡系統,同樣有可能使得量測噪聲與過程噪聲具有異步相關性[16-17];在自動目標識別系統和自動威脅識別系統中,當量測噪聲和過程噪聲同時依賴于系統狀態時,傳感器噪聲與過程噪聲之間也可能會存在相關性[18];同時由于連續系統離散化過程中,系統狀態離散化采樣時將引入額外的噪聲到量測模型中,導致量測噪聲與過程噪聲之間存在一定的時空相關性[19]。因此,在聯合狀態估計和角速度辨識的過程中必須考慮這種相關性。噪聲相關條件下的估計問題可以分為兩大類:同步相關和異步相關。針對噪聲同步相關條件下的狀態估計主要有以下3種框架:噪聲解耦框架、高斯近似遞歸濾波框架和相關高斯近似濾波框架。這3種框架對線性系統或者在最小均方誤差意義下的非線性系統而言是等價的[20]。Bar[13]、Chang[21]、Hu[22]等采用重構偽狀態方程的方式,來達到相關噪聲解耦的目的,并分別設計了擴展卡爾曼濾波、邊緣化的無跡卡爾曼濾波和無跡卡爾曼濾波進行狀態估計;Wang等[23]通過計算兩步狀態后驗預測概率密度函數和一步量測后驗預測概率密度函數,基于二階Stirling插值,設計了新的中心差分濾波器;Huang等[24]通過分析上述兩種框架的缺點,設計了一種新的相關高斯近似濾波框架。針對噪聲異步相關條件下的狀態估計的研究主要有:于浛等[17]針對隨機時滯和異步相關噪聲情況,提出了一種改進的高斯近似濾波算法;Souto和Ishihara[15]針對異步相關噪聲條件下的估計問題設計了一種魯棒擴展卡爾曼濾波算法。
針對上述問題,本文通過將狀態估計與轉彎角速度辨識聯合考慮,基于EM算法框架提出一種帶異步相關噪聲的聯合估計與辨識算法,該算法通過解除目標狀態與轉彎角速度之間的耦合關系,進而獲得轉彎角速度閉環形式的解析解,并引入滑窗思想,以提高辨識的實時性,主要包括E-step和M-step 2個部分:E-step基于當前估計的角速度并利用帶異步相關噪聲的高斯近似濾波器與平滑器獲得的后驗平滑概率密度和聯合分布密度,近似計算完整的對數函數似然函數的期望;M-step通過使期望最大化更新獲得下一次迭代的角速度估計量。
1 問題描述
蛇形機動可以分解成若干個具有不同轉彎角速度的圓弧轉彎機動,因此蛇形機動目標轉彎角速度的辨識問題相應地轉化為圓弧轉彎機動的角速度辨識問題。在帶異步相關噪聲背景下,假設目標在二維平面中運動,轉彎機動模型狀態方程及量測方程為
xk+1=fk(xk,Ωk)+wk
(1)
zk+1=hk+1(xk+1)+vk+1
(2)
式中:
fk(xk,Ωk)=

1.1 基于系統重構的角速度解耦策略
由于蛇形機動目標的轉彎角速度Ωk這一未知參數非線性耦合在狀態轉移矩陣之中,傳統的辨識算法僅能獲得轉彎角速度的近似解,辨識效果不佳,因此為了獲取轉彎角速度的解析解,就需要將轉彎角速度與狀態轉移矩陣之間的非線性耦合關系解除,即在原有系統模型的基礎之上,通過模型的轉換,重構一個新的狀態方程,將轉彎角速度從狀態轉移矩陣中提取出來,從而解除這種耦合性,如式(3)所示:
xk+ 1=F(xk)θ+xk+wk
(3)
式中:
θ3=1-cos(ΩkT)
θ4=sin(ΩkT)
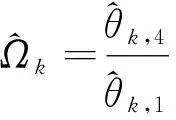
1.2 基于量測重構的異步相關噪聲解耦策略
由于在上述異步相關噪聲條件下,傳統的高斯近似濾波器性能不佳,甚至發散,進而影響EM算法的辨識效果,所以為了實現狀態的精確估計和轉彎角速度的準確辨識,本節通過采用“去相關框架”[25],基于原有的量測模型,對量測模型進行轉換,從而重構一個偽量測方程,使得重構的偽量測方程滿足過程噪聲與量測噪聲之間的相關性解除。在重構的偽量測基礎之上實現濾波和平滑,獲得后驗平滑概率密度和聯合分布密度,進而實現轉彎角速度辨識與狀態估計。
在量測方程式(2)右邊形式地加上一等于零的項:
fk(xk,Ωk)-wk)
(4)
式中:Gk+1為待定矩陣。
記
fk(xk,Ωk))
(5)
(6)
則量測方程轉換成為
(7)

(8)
E[(vk+1-Gk+1wk)(vk+1-Gk+1wk)Τ]=
(9)

(10)
可得
(11)
(12)
2 基于HCKS-EM的聯合估計與辨識算法
基于極大似然估計準則[26-27],本文提出了一種帶異步相關噪聲的聯合狀態估計與角速度辨識算法,具體的算法框架如圖1所示。在第t次迭代時,利用帶異步相關噪聲的高斯近似濾波器與平滑器,獲得目標狀態的平滑估計量,并采用EM算法進行參數θ的辨識,辨識后的參數θ用于第t+1次的狀態估計,不斷迭代直到滿足設定的要求為止。

圖1 聯合估計與辨識Fig.1 Joint estimation and identification
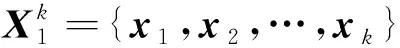
(13)
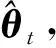
(14)
式中:
(15)
(16)
(17)
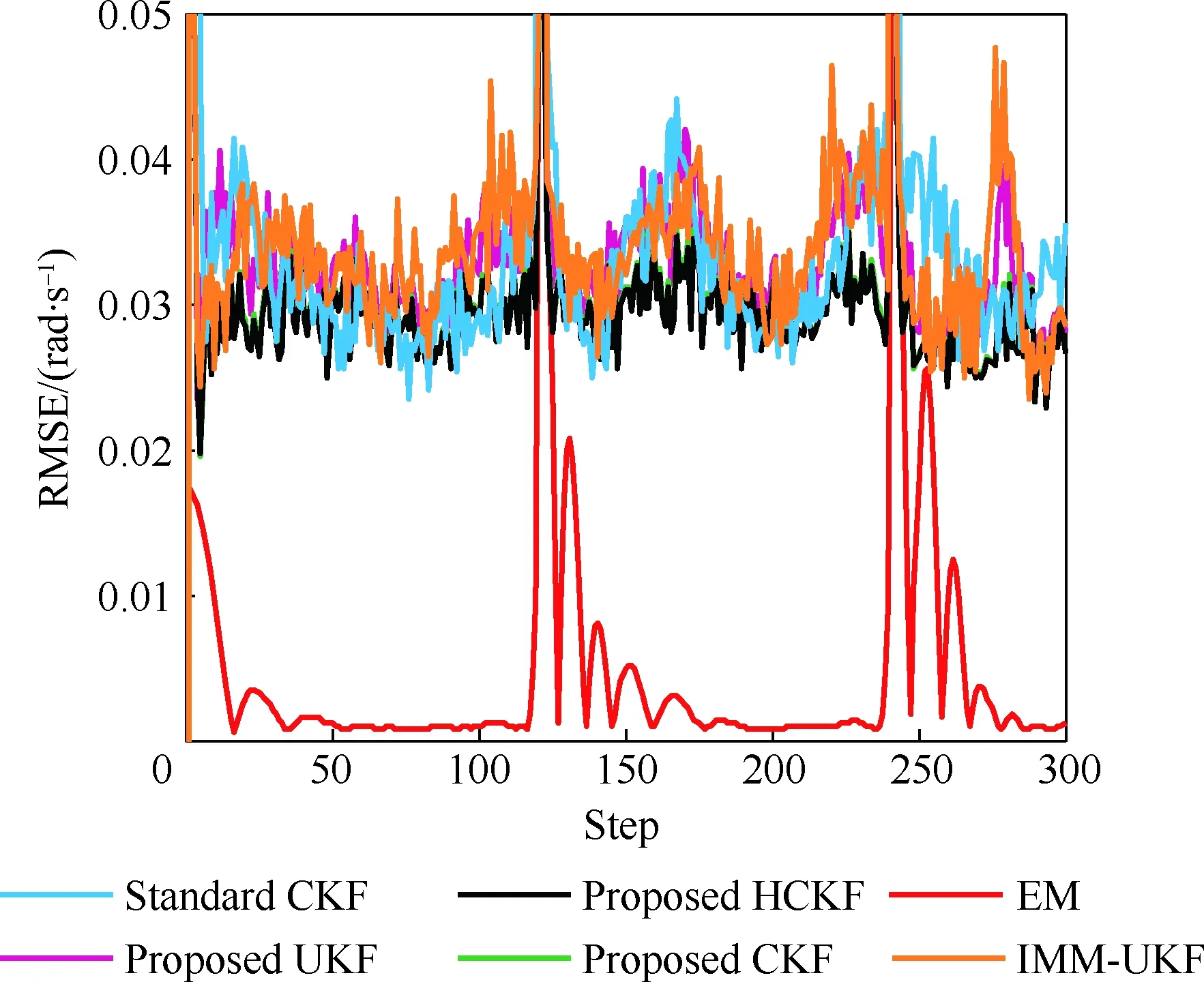
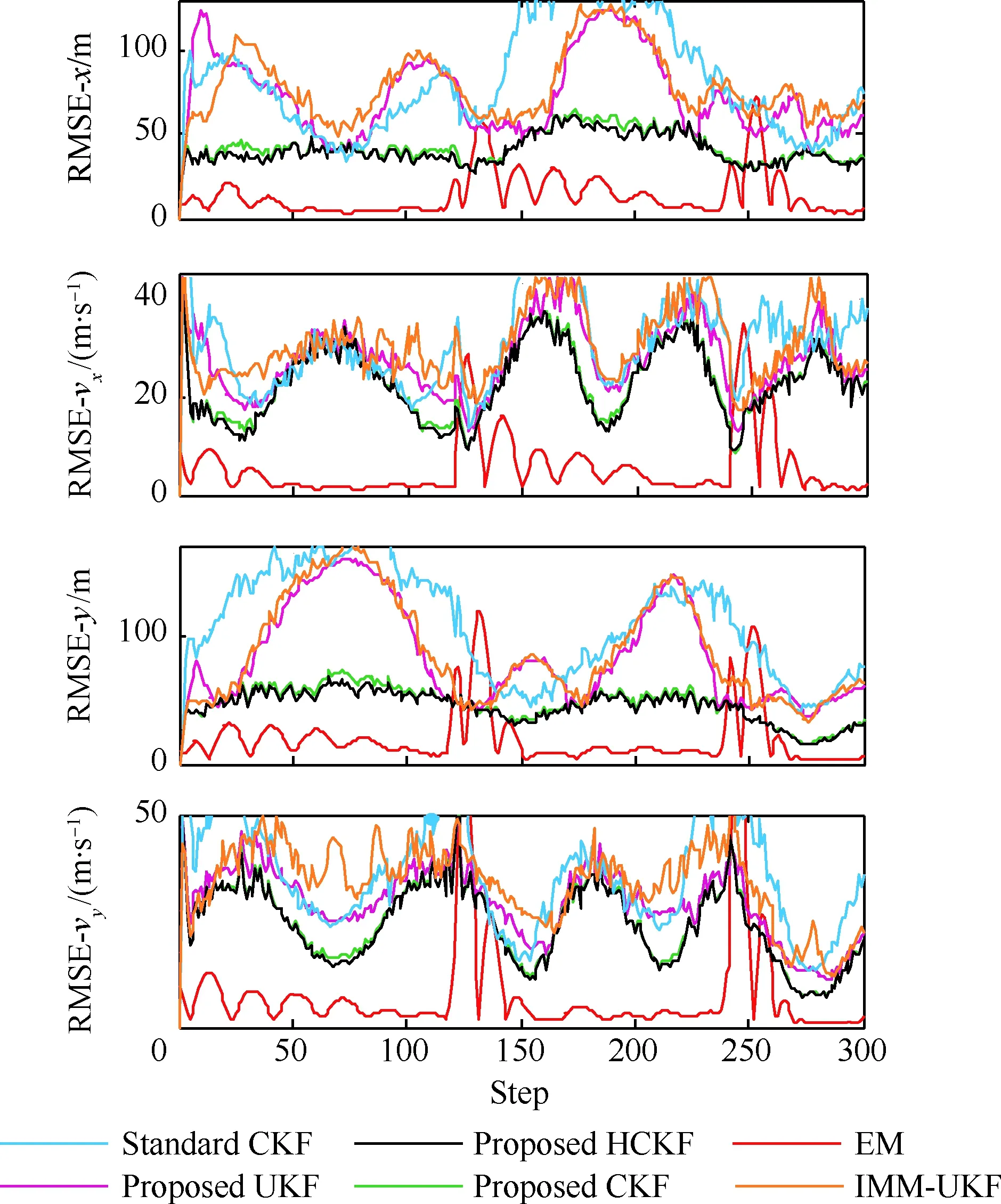
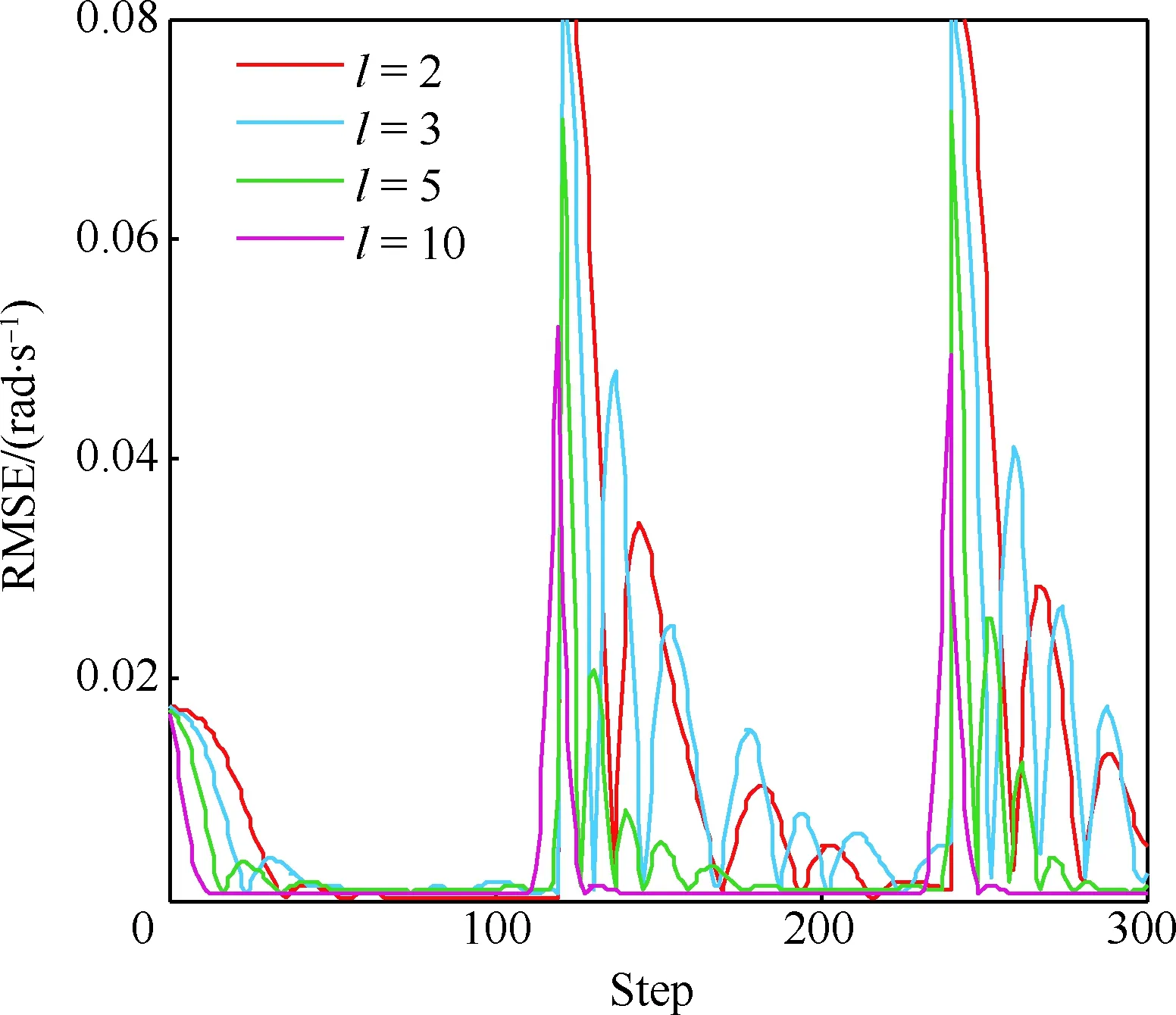
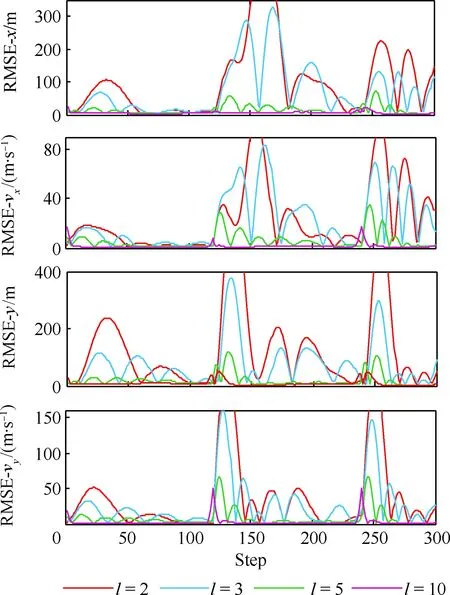
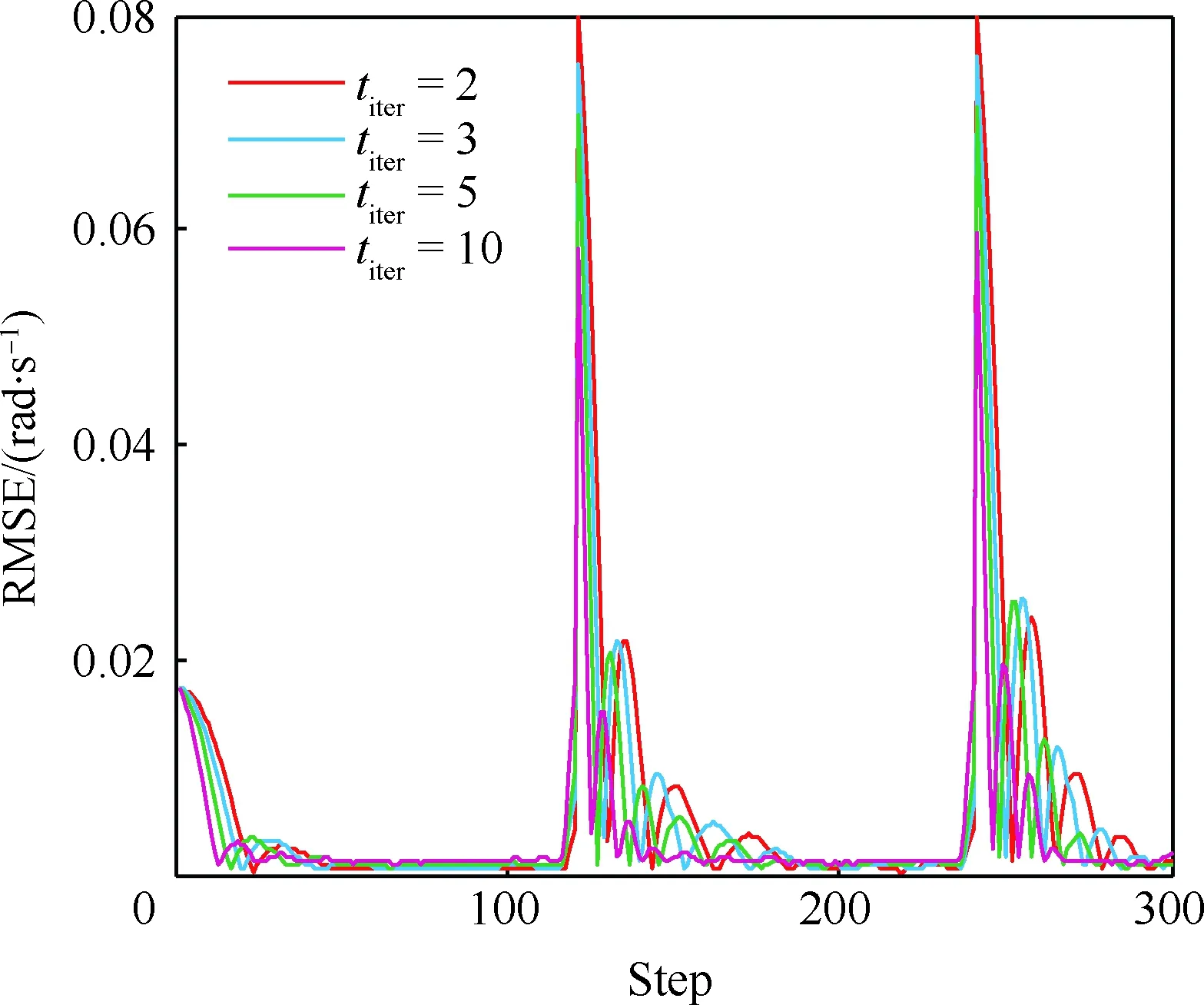
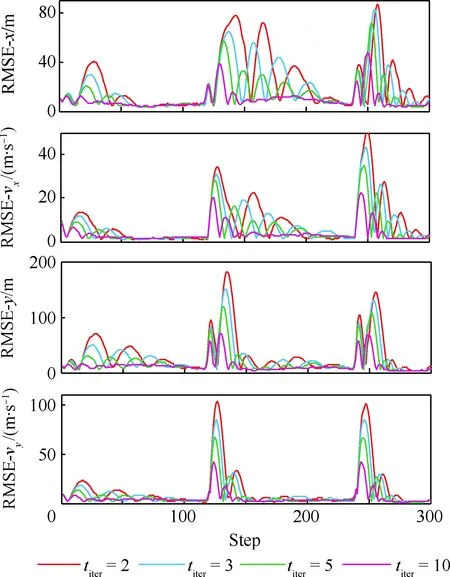
當l=k-1時,I1是一個常數,與待辨識量θ無關;當0≤l pθ(xk-i|xk-i-1)~N(xk-i;F(xk-i-1)θ+xk-i-1,Q) (18) (19) 跟據貝葉斯準則得到xk-i和xk-i-1的聯合概率密度分布: (20) 采用帶異步相關噪聲的HCKS平滑器得到平滑概率密度時,將基于以下假設: 服從高斯分布[29]。 (21) 式中: 則 (22) (23) (24) (25) 將式(21)和式(23)代入(20)的聯合分布,有 (26) 到k-i-1時刻的平滑分布為 (27) (28) (29) 為了求解I2,首先定義如下兩種積分函數: (30) Δ(xk-i,xk-i-1)=?F(xk-i-1)TQ-1(xk-i-xk-i-1)· (31) 然后分別將F(xi)、xi按xi的分量進行分解: (32) (33) (34) (35) 則 (36) (37) 本文采用Jia等提出的五階球面徑向容積規則[5]解決帶異步相關噪聲的高斯近似濾波器和平滑器中的非線性高斯積分的計算問題。基于容積規則的高斯積分求解可抽象成為 (38) (39) 式中:ej為空間Rn中的單位向量,其第j個元素為1;權值ws1和ws2分別為 (40) (41) 由矩匹配法可知,五階徑向規則當中,容積點與權重需要滿足: (42) (43) (44) 將式(39)、式(43)和式(44)代入式(38)可得 (45) 由式(45)可知五階容積規則的采樣點數量為 2n2+1。 M-step的主要任務是解決I2的極大化問題,即求解使I2滿足極大值時所對應的θt+1值,用于EM算法的下一次迭代更新: (46) 當I2取得極大值時滿足: (47) 則可求得參數θ的迭代表達式為 (48) 本文采用的是滯后窗口,即辨識k-l時刻的參數θ的值需要使用[k-l,k]時刻的量測,然后通過反解參數θ與參數Ω之間的函數關系,求得k-l時刻目標的轉彎角速度的辨識結果。 本文算法總結如表1所示。 表1 基于HCKS-EM的聯合估計與辨識算法 基于HCKS-EM的聯合估計與辨識算法的收斂性受帶異步相關噪聲濾波算法的收斂性以及EM算法的收斂性兩個方面的影響。 對于EM算法的收斂性而言,為了更好地說明該算法的收斂性,需要給出以下定理: ?t=1,2,… (49) (50) 令 (51) (52) (53) (54) (55) 對于式(54)右邊第二項而言,已知當x≥0時,滿足:lnx≤x-1,則 (56) 同樣從式(54)~式(56)可以看出 (57) 本文利用水平方向上的轉彎機動非線性動態模型,仿真出一條蛇形機動軌跡。假設機動目標在1~120 s以Ω1=-2 (°)·s-1作轉彎運動,在k=121 s時轉彎角速度突變為Ω2=3 (°)·s-1作轉彎運動,在k=241 s時轉彎角速度突變為Ω2=-2 (°)·s-1作轉彎運動,并持續到300 s。設置轉彎角速度初始值為Ω0=-1 (°)·s-1,采樣周期T=1,q1=0.1 m2/s3,wk為零均值高斯白噪聲,其協方差為Q。 通過載機雷達可以獲得目標與載機之間的相對距離r、方向角φ的信息,則可獲得系統的非線性量測方程為 本文提出的聯合估計與辨識算法和擴維法的初始狀態以及協方差分別設置為 初始狀態: 初始協方差: P0= diag(100 m2,10 m2·s-2,100 m2,10 m2·s-2) 擴維法初始狀態: 擴維法協方差: 100 mrad/s) 為了評估分析本文提出算法的性能,首先將本文算法與傳統的擴維法以及基于UKF的交多模型算法(IMM-UKF)[32]進行對比分析。IMM-UKF算法采用了標準維納過程速度模型和擴維的勻速轉彎模型兩種機動模型,并且兩種機動模型的狀態和協方差的初始值以及量測噪聲和過程噪聲設置與上文保持一致。維納過程速度模型的狀態轉移矩陣為F,量測矩陣為H,表達式分別為 IMM-UKF算法中模型之間的轉移概率矩陣為Π,初始模型概率矩陣為μ,表達式分別為 本文提出的聯合估計與辨識算法采用滑窗機制,窗口設置為5,最大迭代次數為5次,各執行100次蒙特卡羅仿真。圖2和圖3分別為上述3種 算法對角速度辨識和目標狀態估計的效果,從圖2和圖3中可以看出,本文提出的聯合估計與辨識算法在角速度辨識和目標狀態估計上比傳統的擴維法以及IMM-UKF算法誤差小,精度高,這主要是因為本文提出的算法解除了角速度與狀態方程之間的耦合關系,從而便于獲得角速度辨識的解析解,并且,采用了閉環反饋的處理方式,通過反復的迭代不斷修正角速度辨識與目標狀態估計的誤差,從而提高了辨識與估計的精度。而且從圖2和圖3中發現,基于IMM-UKF算法的角速度辨識和目標狀態估計的均方根誤差要比傳統的擴維法大,這主要是因為交互多模型算法處理的是目標跟蹤時發生的模型不匹配問題,但是本文設計的蛇形機動仿真采用的是單一的勻速轉彎模型,所以交互多模型算法的優勢并未體現出來,產生的辨識與估計效果不佳。從圖中可進一步看出,在異步相關噪聲背景下,帶異步相關噪聲的高斯近似濾波器的估計與辨識效果優于傳統的標準的高斯近似濾波器,這主要是因為,本文所提到的帶異步相關噪聲的高斯近似濾波與平滑算法采用了“去相關”框架,通過重構偽量測方程,解除了量測噪聲與過程噪聲之間的相關性,在目標狀態與量測相互獨立的基礎上設計的濾波算法顯然性能優于傳統的濾波算法,并從圖中可看出高階容積卡爾曼算法估計與辨識效果優于容積卡爾曼算法和無跡卡爾曼算法,尤其是在量測噪聲和過程噪聲增大時,這種優越性就越明顯,但是相應的計算量就會增加,計算時間增大,主要是因為高階容積卡爾曼算法的采樣點數量高于容積卡爾曼算法和無跡卡爾曼算法。 圖2 角速度辨識均方根誤差Fig.2 RMSE of turn rate identification 圖3 位置和速度估計均方根誤差Fig.3 RMSE of position and velocity estimation 其次,從該算法的本身結構著手,對該算法進行評估分析。主要從窗長和迭代次數兩個方面分析。采取滑動滯后窗口策略,窗口長度l分別設置為2、3、5、10,最大迭代次數均為5次,各執行100次蒙特卡羅仿真。從圖4和圖5中可以看出,隨著窗口長度的增大,該算法收斂于真實值的時刻就越早,精度越高,當角速度發生突變時,對于突變的角速度反應也越快。并且從圖6和表2可以看出,窗口長度越大,該算法估計的目標狀態整體精度就越高,但是消耗的時間越長,這顯然是時間與精度之間的“博弈”問題,從圖中還可以進一步看出,當窗長大于5時,由窗長帶來的精度效益不太明顯,相反時間消耗問題更加突出。 圖4 不同窗口長度下角速度辨識結果Fig.4 Identification result of turn rate with different window length 對于迭代次數而言,將窗口長度l設置為5,最大迭代次數titer分別設置為2、3、5、10,各執行100次蒙特卡羅仿真。從圖7和圖8中可以看出,隨著迭代次數的增加,該算法在收斂于真實值的時刻就越早,并且對于角速度突變反應的也比較靈敏,角速度辨識的精度也越高。 圖5 不同窗口長度下角速度辨識均方根誤差Fig.5 RMSE of turn rate identification with different window length 圖6 不同窗口下位置和速度估計均方根誤差Fig.6 RMSE of position and velocity estimation with different window length 表2 計算k=37 s時的角速度和狀態所耗費的時間 Table 2 Time cost for calculating turnrate and states at k=37 s 滑動窗口長度l=2l=3l=5l=10時間/s0.013 60.019 30.032 40.056 2 圖7 不同迭代次數下角速度辨識結果Fig.7 Identification result of turn rate with different iterations 圖8 不同迭代次數下角速度辨識的均方根誤差Fig.8 RMSE of turn rate identification with different iterations 表3 計算k=47 s時的角速度和狀態所耗費的時間 Table 3 Time cost for calculating turnrate and states at k=47 s 最大迭代次數titer=2titer=3titer=5titer=10時間/s0.010 30.016 30.026 40.054 2 圖9 不同迭代次數下位置和速度估計均方根誤差Fig.9 RMSE of position and velocity estimation with different iterations 從圖9目標狀態4個分量的RMSE可以看出,迭代次數越大,該算法估計的目標狀態整體精度就越高,但是從表3顯示的不同迭代次數下計算k=47 s時的角速度和狀態所耗費的時間越大,性價比不高。尤其是當迭代次數大于5時,由迭代次數帶來的精度效益遠遠比不上時間帶來的損耗,降低該算法的實時性。 1) 在E-Step,采用系統重構角速度解耦策略解除了轉彎角速度與狀態轉移矩陣之間的耦合特性,在此基礎上將完備似然函數進行分解,從而將其轉換成帶參數θ的解析表達式,降低了由于狀態擴維法擴維所帶來的復雜性;通過采用量測重構噪聲相關性解耦策略,解除過程噪聲與量測噪聲之間的異步相關耦合特性,基于貝葉斯框架,設計了帶異步相關噪聲的高斯近似濾波和平滑算法,并基于該算法獲得了目標狀態的平滑估計。 2) 在M-Step中,通過極大化完備似然函數求得轉彎角速度閉環形式的解析解,降低了辨識風險,提高了狀態估計精度。 3) 仿真實驗表明,本文提出的聯合估計與辨識算法性能優于傳統的擴維法以及交互多模型算法。
2.1 E-step


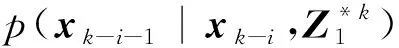

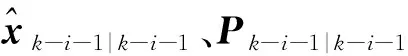
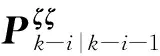

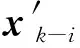
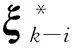


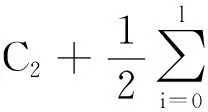


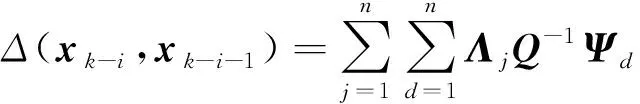
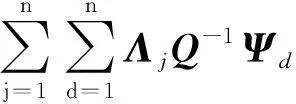
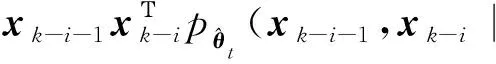
2.2 五階球面-徑向容積規則
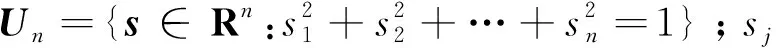



2.3 M-step

2.4 收斂性分析






3 仿真分析

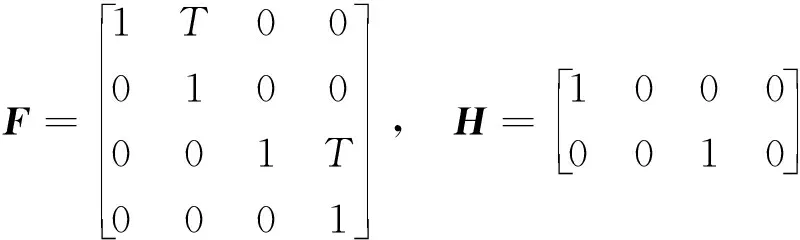
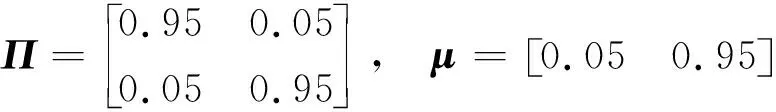




4 結 論

