改進型混合式永磁調速器的優化設計

高慶忠，袁 波，陳 鵬,呂鵬飛，李晟宇，邱力偉

(1.沈陽工程學院，沈陽 110136；2.遼寧蒲石河抽水蓄能有限公司，丹東 118000)

0 引 言

混合式永磁調速器(以下簡稱HAPMC)主要由導體轉子、永磁轉子以及調節裝置[1]構成，如圖1所示。它是一種純機械結構無外接電源利用渦流效應傳遞扭矩，放置于原動機與負載之間實現了能量的非接觸傳遞，并且可以通過調節機構調節扭矩和轉速。

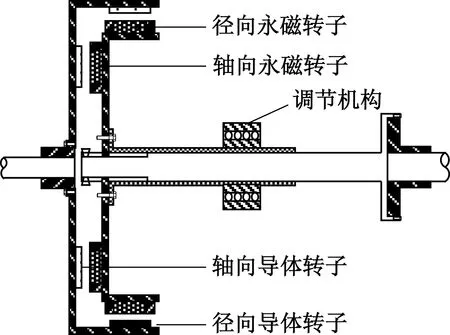
圖1 HAPMC結構圖

永磁調速器的優化設計方法大致可以分為有限元法[2]與優化算法2種。與有限元法相比，使用優化算法對永磁調速器進行優化設計會使得結果更加精確，國內外專家學者對此作了大量的研究。

2002年，英國學者Smith AC和美國學者Wallace A以經濟高效為目的，建立了永磁調速器的二維線性層解析模型，并且使用不同優化算法進行優化設計，對比了結果[3]。

2014年，美國愛達荷大學Amged S El-Wakeel 運用粒子群-單純形法混合算法對永磁渦流耦合傳動裝置進行優化設計，并與單純使用粒子群法或者單純形法的優化結果進行了對比，證明了該混合算法的先進性[4]。

2016年，山西農業大學李旭貞等人采用罰函數法建立永磁調速器主要設計參數與目標函數之間關系的解析模型，并完成了永磁調速器主要參數的優化。優化設計后的結果與傳統設計相比，可以提高設備使用范圍、傳動效率并可降低檢修頻率[5]。

上述方法均為針對單向永磁調速器的優化設計方法，未考慮HAPMC的優化，并且在優化過程中選擇的性能指標過少，難以達到設備性能的全面優化。鑒于這種情況，本文提出一種改進型和聲搜索算法，它基于和聲記憶庫信息構成反饋機制、轉變和聲搜索算法尋優策略，在此過程中充分考慮了和聲記憶庫外部信息引入及和聲記憶庫內部信息共享的有效性，從而較好地平衡了算法的探索和開采能力，并將其成功用于改進型HAPMC的優化設計。

1 優化問題的提出

1.1 優化參數的選擇

傳統的永磁調速器多采用瓦片形磁極，這導致其氣隙磁密中含有大量的諧波，對設備的性能造成了極大的負面作用。為了減少氣隙磁密的諧波含量，本文對永磁轉子結構以及陣列排布進行改進，設計了一種改進型HAPMC來解決磁場耦合問題，圖2為改進前后永磁轉子示意圖。

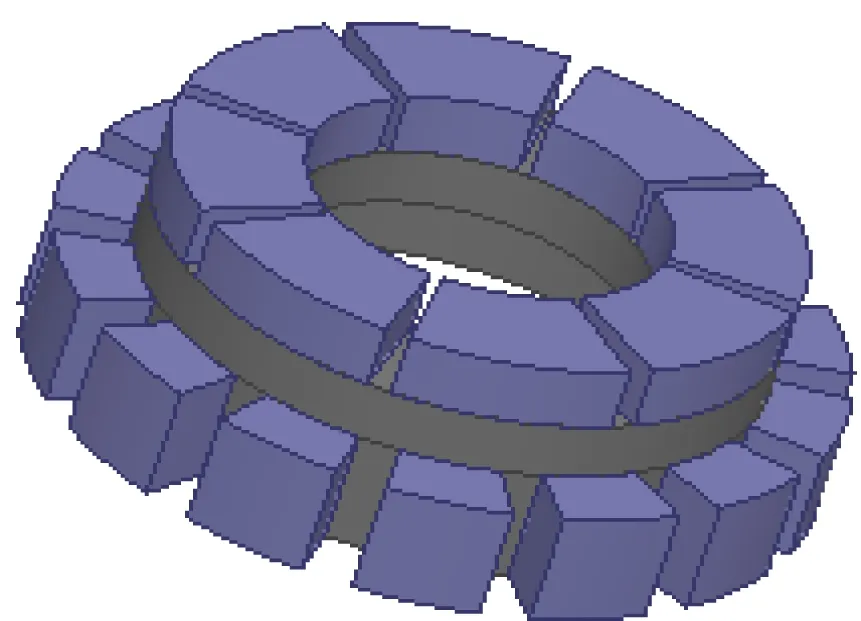
(a) 改進前的永磁轉子

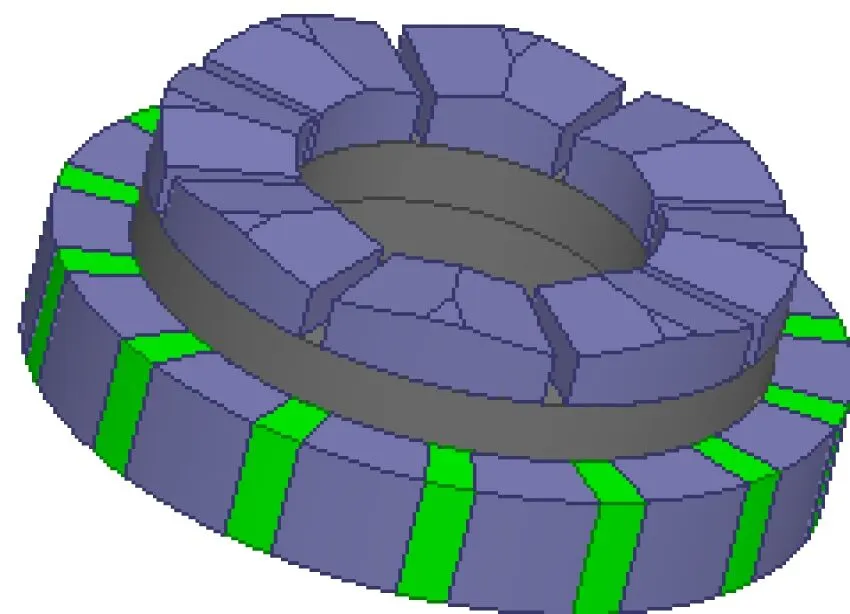
(b) 改進后的永磁轉子圖2 永磁轉子改進示意圖

在軸向永磁轉子的設計中，本文擬采用弧形表面磁極代替瓦片形磁極，但是考慮到弧形表面工藝的復雜程度及高成本，故采用梯形表面磁極取代弧形表面磁極。由正弦優化原理可知，采用梯形磁極可以改善氣隙磁密波形質量，進而優化設備性能，文獻[6]對此結論已有相關證明。徑向永磁轉子的磁路結構采用90°Halbach永磁陣列[7]，一方面該結構的單邊聚磁效應[8]能夠顯著增強氣隙磁密進而提高其輸出轉矩;另一方面采用Halbach型永磁體陣列還能夠改善氣隙磁密的正弦性，進而削弱設備的電磁轉矩脈動。

為了便于下文對改進型HAPMC參數的優化，對改進后的永磁轉子相關參數作出如下定義：軸向磁極的切割角度θ、切割高度h如圖3所示，磁極配比以及極弧系數定義見文獻[8]。

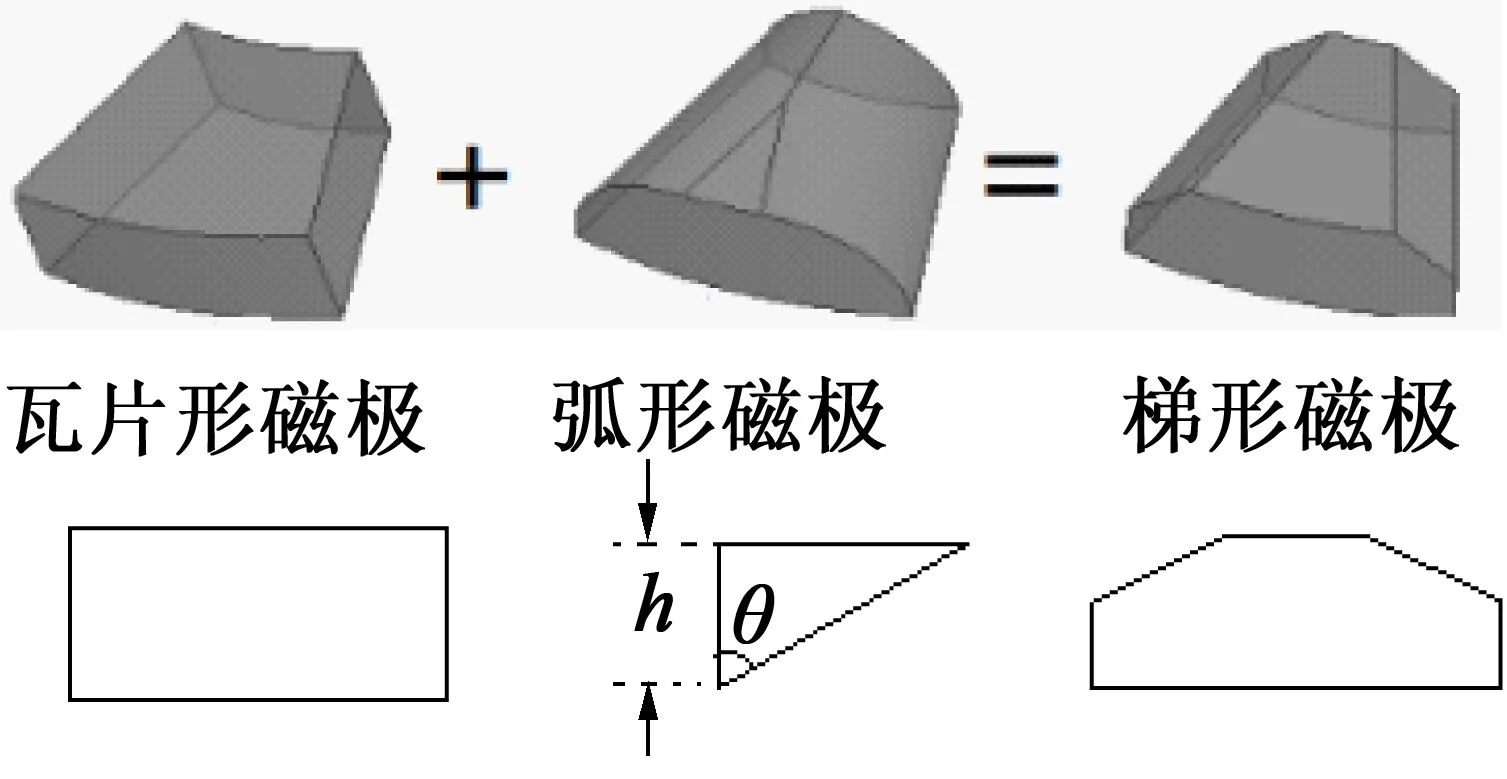
圖3 軸向磁極優化參數示意圖

對永磁調速器性能產生影響的主要結構有銅環(盤)尺寸、永磁轉子對數以及尺寸，而背襯(內襯)鋼環對其性能的影響微乎其微，可以忽略。綜上所述，本文優化設計參數的選擇如下：徑向永磁轉子磁極對數pj，徑向永磁轉子厚度hMj，Halbach永磁陣列的磁極配比αj，徑向銅環厚度hjt，軸向永磁轉子磁極對數pz，軸向永磁轉子厚度hMz，軸向磁極的極弧系數αz，切割角度θ，切割高度h以及軸向銅盤厚度hzt,改進型HAPMC的原始參數范圍如表1所示。

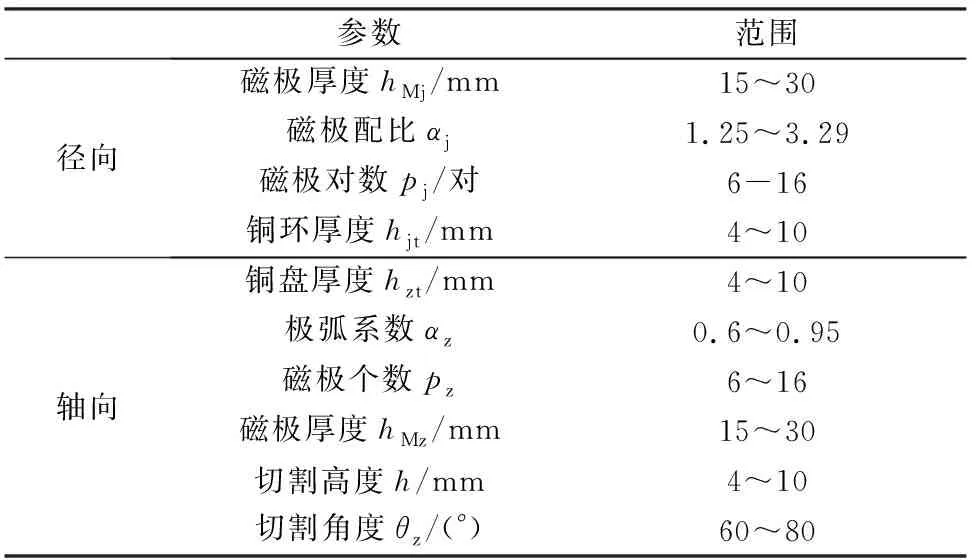
表1 原始參數范圍

2.2 優化函數的提出

盡管永磁轉子改進結構以及設備整體結構得以確定，但是如果參數選擇不當，仍然會對設備乃至整個系統造成危害，因此需要確定一種參數優化方法對改進設備進行優化。優化參數在前文已經確定，本文選擇HAPMC的輸出轉矩T、渦流損耗ploss以及氣隙磁密波形畸變率kBδ為優化的性能指標。

根據表1的改進型HAPMC的參數范圍，建立改進型HAPMC優化問題的數學模型，并確定了目標函數的約束條件，如式(1)和式(2)所示。其他結構參數設為固定值，范圍如表1所示。

(1)

(2)

運用優化算法，多個性能指標同時進行優化是一個多目標求解問題。多目標優化問題比較復雜并且陷入局部最優的概率更大，因此在優化之前需要對其進行處理，這類問題的處理方法：一是求取非劣解集，然后手動選取最優解；二是轉為單目標問題求解。本文采用第二個方法，將多目標轉為“綜合滿意度”這一單目標問題進行求解。定義T，ploss和kBδ的“滿意度”分別為式(3)、式(4)和式(5)，定義3個指標的“綜合滿意度”為式(6)。

(3)

(4)

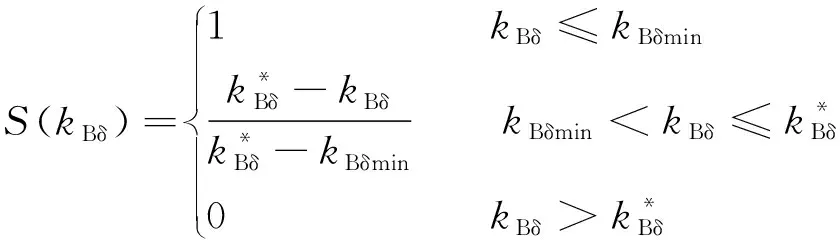
(5)

Sc(T,ploss,kBδ)=min {S(T),S(ploss),S(kBδ)}

(6)

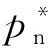
obj:max {Sc(T,ploss,kBδ)}

(7)

即求解滿意度最大時的結構參數，此時約束條件不變，仍然是式(2)。至此，多目標的優化模型式(1)轉化為單目標模型式(7)。

3 預測模型的建立

HAPMC目標函數是復雜的非線性函數，不難看出，式(1)難以用確切的公式表達，因此建立性能指標與優化參數之間關系的預測模型是一個行之有效的方法。建立預測模型的方法之一是支持向量回歸機，在這方面諸多的專家學者進行了深入研究[9-12]。本文采用文獻[13]的永磁調速器的預測模型建模方法，對改進型HAPMC進行建模，步驟如下：

1) 構造訓練樣本

利用面心立方復合設計方法[13]構造出具有50個訓練的輸入樣本，并利用Maxwell Ansoft軟件計算輸出樣本后得到訓練樣本，表2為部分訓練樣本。 2) 建立預測模型基于支持向量機建立改進型HAPMC預測模型，定義均方根誤差和復測定系數2個指標[13]，用以保證預測模型的準確性。性能指標T,ploss,和kBδ的均方根誤差和復測定系數為0.273 1,0.897 5,0.198 4和0.224 5,0.913 2,0.210 3，這說明回歸預測模型準確度較高。

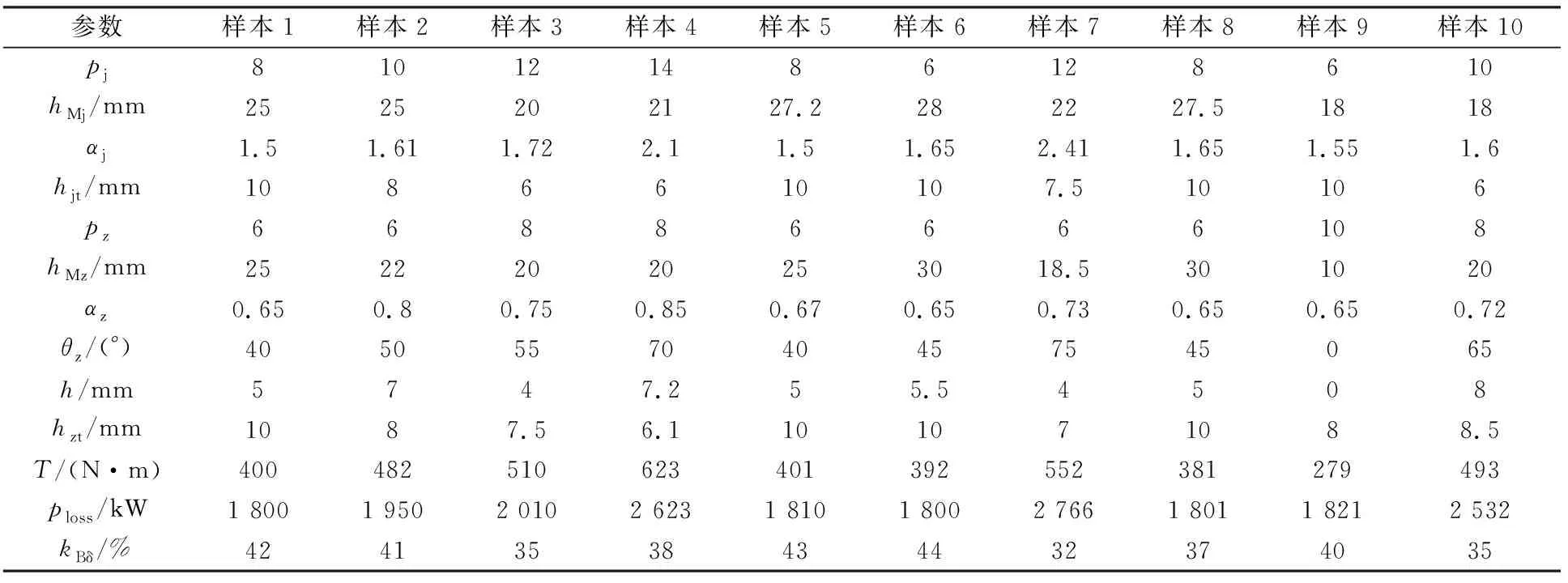
表2 部分訓練樣本

3) 預測結果分析

改進型HAPMC的渦流損耗ploss、輸出轉矩T以及氣隙磁密波形畸變率kBδ的預測模型建立后，進行仿真測試，隨機選取10組訓練樣本外的試驗數據作為測試樣本對預測回歸模型進行測試，表3列出了部分用于測試的數據及性能的試驗值與預測值。

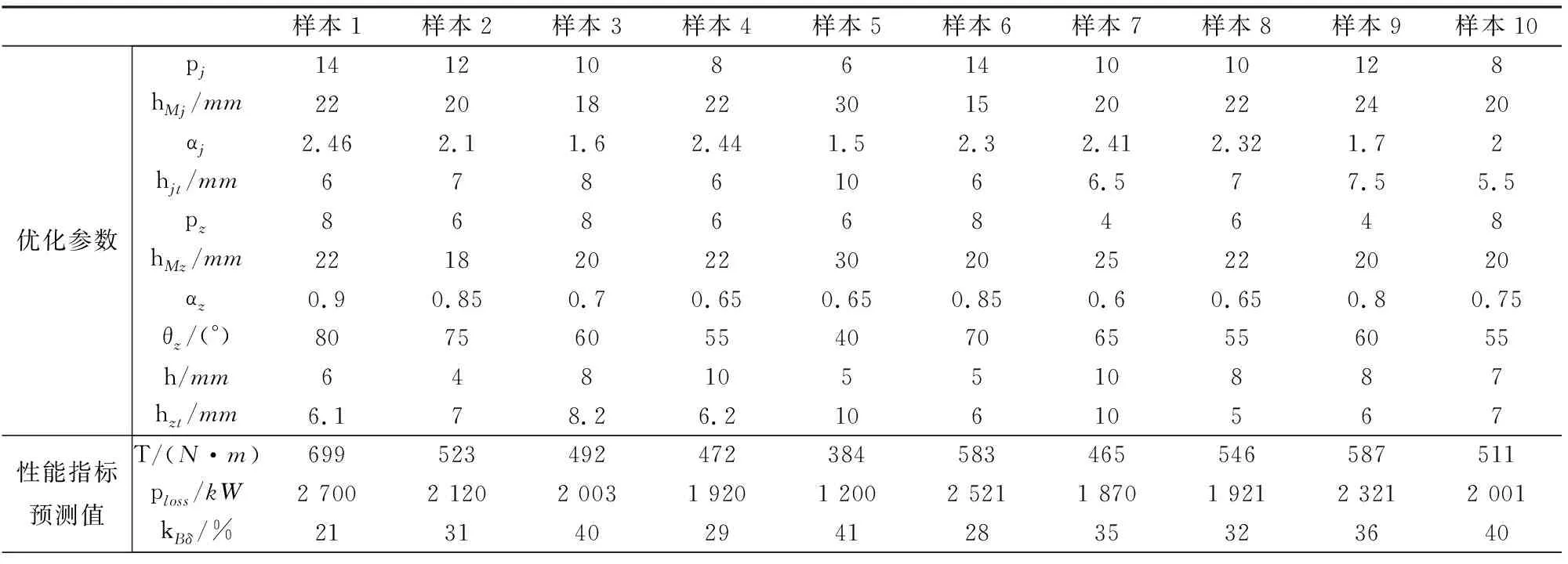
表3 試驗值與預測值的對比

續表

從表3中可以明顯看出,本文預測方法預測值與有限元試驗的數值基本吻合，但是仍存在一定誤差。誤差產生的原因有很多,可能是訓練樣本數量較少造成的,可能是有限元模型的環境因素造成的，也有可能是其它因素造成的。以上誤差幾乎是難以避免但也是允許的，因此在誤差允許的范圍內，認為本文構造的預測模型是準確的。

4 預測模型的優化求解

和聲搜索算法將樂器聲調的和聲類比于優化問題的解向量，評價即是各對應的目標函數值[14]。本文的改進和聲搜索算法，是在給定種群多樣性、停滯狀態定義的基礎上，對算法的新和聲產生機制和搜索策略進行改進，以便使算法既具有較好的全局探索能力，又具有較好的局部開采能力。

4.1 改進和聲搜索算法

4.1.1 探索策略

恰當的探索策略可以提高優化算法探索能力，進而增強其全局尋優能力，避免算法陷入局部最優。為了對該搜索策略進行描述，本文進行如下定義：

定義1 分量熵值

設和聲記憶庫中包含m個和聲向量，每個向量包含n個變量，則群體中第j個分量的熵值Hj可定義[13]：

(8)

(9)

4.1.2 開采策略

開采策略旨在提高算法開采能力，具有優秀開采能力的個體具有更強的局部探索能力。為了說明開采策略，本文進行如下定義：

定義2 和聲記憶庫熵值[15]

整個群體的熵值H定義為群體中所用分量熵值Hj的平均值，即：

(10)

定義3 停滯狀態

和聲搜索算法經過有限次迭代后，和聲記憶庫中的和聲記憶庫熵值未發生變化，則稱算法處于停滯狀態。

算法處于停滯狀態時，說明基于探索策略目標函數的數值不理想，即和聲記憶庫中的和聲向量不會更新，只會徒勞地增加搜索時間，因此需要改變搜索策略。本文提出利用和聲記憶庫中當前和聲向量信息進一步深入開采最優解，開采策略主要融入了人工螢火蟲算法思想，把和聲記憶庫中的每一個和聲向量看作一只螢火蟲，其搜索機制就轉化為基于每一只螢火蟲的熒光亮度這一參數，確定螢火蟲的移動方向；基于螢火蟲的吸引度這一參數，確定螢火蟲的移動距離。這2個參數的具體定義[16,17]如下：

定義4 螢火蟲的熒光亮度

I=I0·e-γrij

(11)

式中：rij表示螢火蟲i與j的路徑長度；γ是常數，稱為光強吸收系數，代表螢火蟲亮度隨路徑長度增加而逐漸減弱的特征；I0為rij=0時的最大熒光亮度，其數值與目標函數值成正比。

定義5 螢火蟲的吸引度

(12)

式中：β0為rij=0螢火蟲的吸引度，即最大吸引度。

位置更新方式見定義6。

定義6 螢火蟲i向螢火蟲j運動路徑的位置更新公式

xi=xi+β(xj-xi)

(13)

4.1.3 算法的流程

算法的流程如下：

1) 相關定義與參數處理

優化問題的定義如下：

f(x) :xi∈Xi(i=1,2,…,N)

(14)

式中：f(x)是目標函數，X是由決策變量xi構成的和聲向量，Xi是每個決策變量xi的所有可能解，N是決策變量的數目。改進和聲搜索算法需要初始化的參數包括和聲記憶庫大小nα，最大迭代次數nmax，嘗試次數n和極限次數nlimit。

2) 初始化和聲記憶庫

隨機生成nα個和聲向量構成初始和聲記憶庫，可表示：

(15)

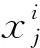
3) 產生一個新的和聲

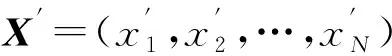
① 探索策略

新解的分量從解分量可行域中隨機選擇產生，但對其分量熵值具有一定的要求，可用下式表示：

(16)

若新和聲的分量滿足式(16)，則接收該新和聲的分量；否則，拒絕該和聲分量，重新產生一個新的和聲分量，執行n次后如仍不滿足要求，則基于和聲記憶庫考慮產生新的和聲。如果和聲記憶庫熵值連續nlimit次迭代未發生變化，則執行開采策略。

② 開采策略

計算每一個和聲向量目標函數值作為每一只螢火蟲的最大熒光亮度I0，由式(11)、式(12)計算螢火蟲的相對亮度I和吸引度β，根據式(13)更新螢火蟲的空間位置。

4) 更新和聲記憶庫

X′是新產生的和聲向量，如果其目標函數值優于最差的Xworst的目標函數值，則用X′代替Xworst，否則保留Xworst到下一代。

5) 核查終止準則

終止運行的條件是當前迭代次數大于最大迭代次數nmax，否則返回流程3)。

4.2 預測模型的優化求解流程

改進型永磁調速器的優化流程如圖4所示，優化步驟具體如下：

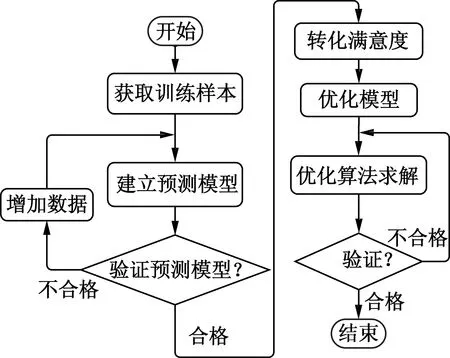
圖4 優化求解流程

1) 獲取建模數據。利用面心立方復合設計方法建立待優化參數的集合，使用Maxwell Ansoft軟件建立三維有限元模型并計算出參數集和對應性能指標，最終構造出訓練樣本。

2) 基于合成核分類近似支持向量回歸機方法，建立預測模型并采用后重交叉驗證法確定各參數值[13]，選取訓練樣本以外的參數驗證預測模型的準確性。

3) 將多目標優化問題轉化為單目標優化函數及滿意度函數，并建立轉化之后優化問題的數學模型。

4) 利用改進和聲搜索算法對預測模型進行求解，通過仿真分析驗證其合理性。

根據圖4的優化設計流程，計算得到改進型HAPMC的結構參數以及對應的性能指標，同時給出了文獻[18,19]的優化結果，對比結果如表4所示。

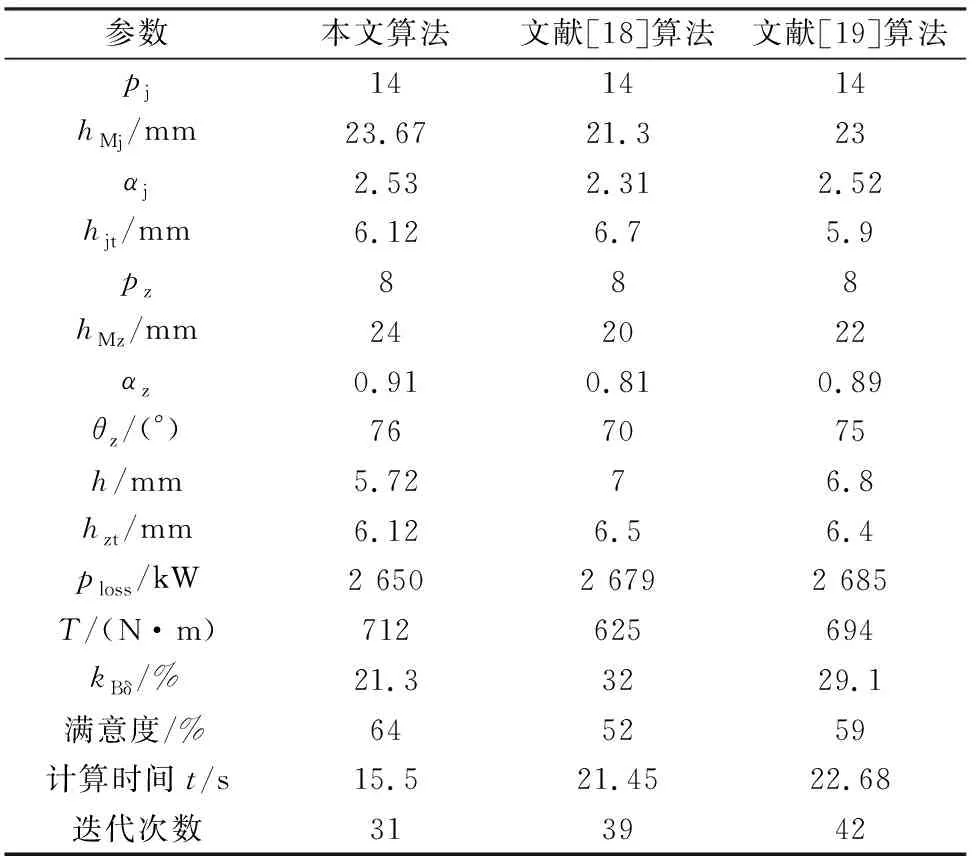
表4 優化結果

由表4可以得出如下結論：

1) 文獻[18,19]的優化算法已經被應用于永磁調速器的優化設計,并取得了較好的效果，但是，本文的優化算法結果更好，滿意度最大，達到了64%；

2) 從計算時間上來看，本文完成優化求解所用的時間少,為15.5 s，這說明了本算法的優化求解速度快。

3) 從迭代次數上來看，本文完成優化求解的迭代次數少,為31次，這說明了本算法的優化求解效率高。

4.3 仿真驗證

4.3.1 渦流仿真研究

分別對采用本文優化方法以及采用文獻[18,19]優化方法得到的改進型HAPMC進行渦流仿真，圖5為不同優化方法得到的徑向銅環以及軸向銅盤渦流分布的仿真結果。

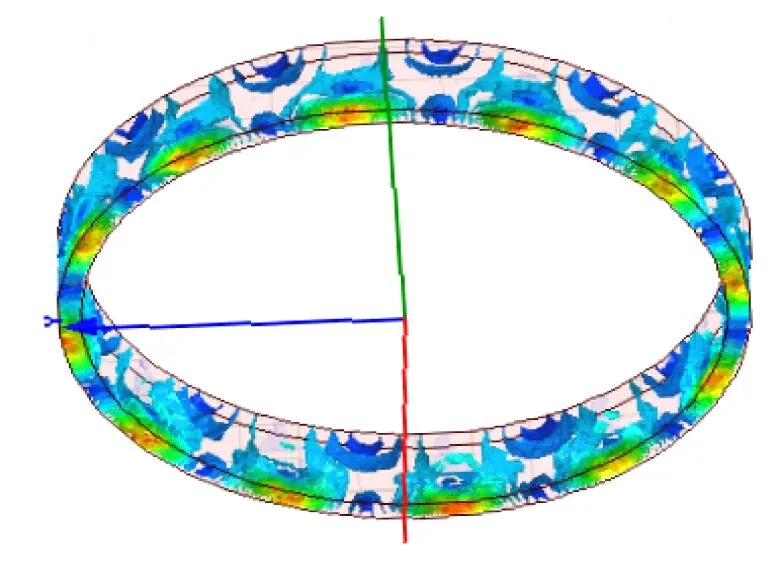
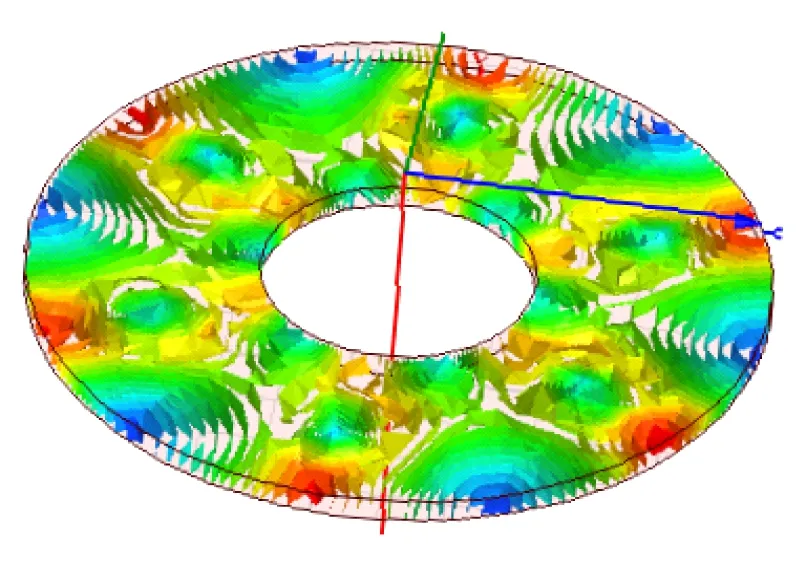
(a) 文獻[18]優化結果

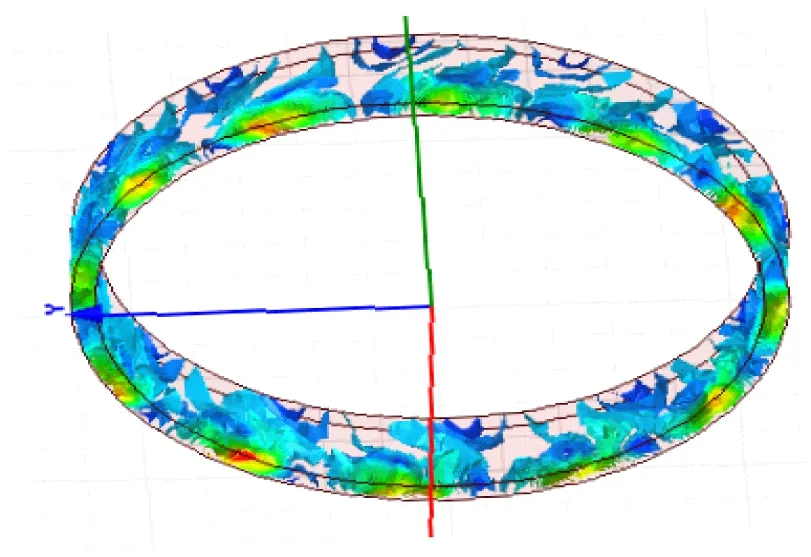
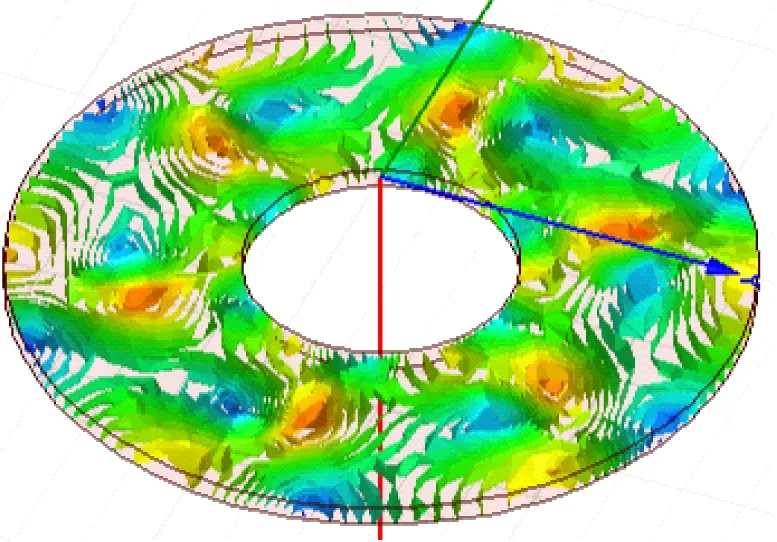
(b) 文獻[19]優化結果

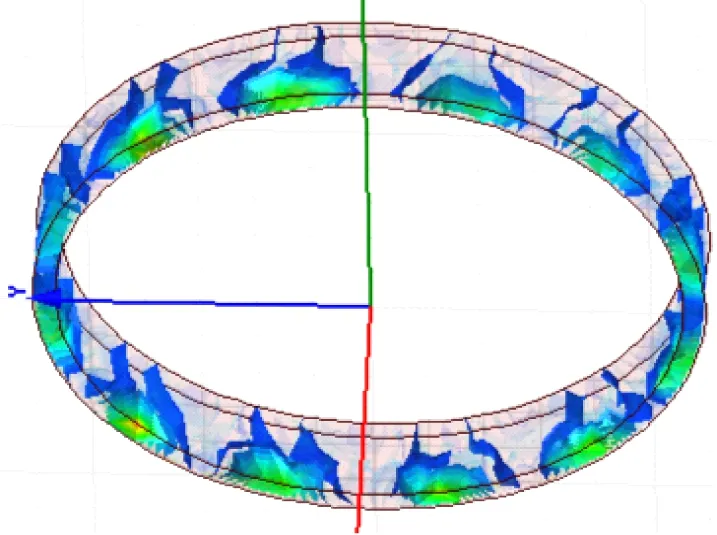
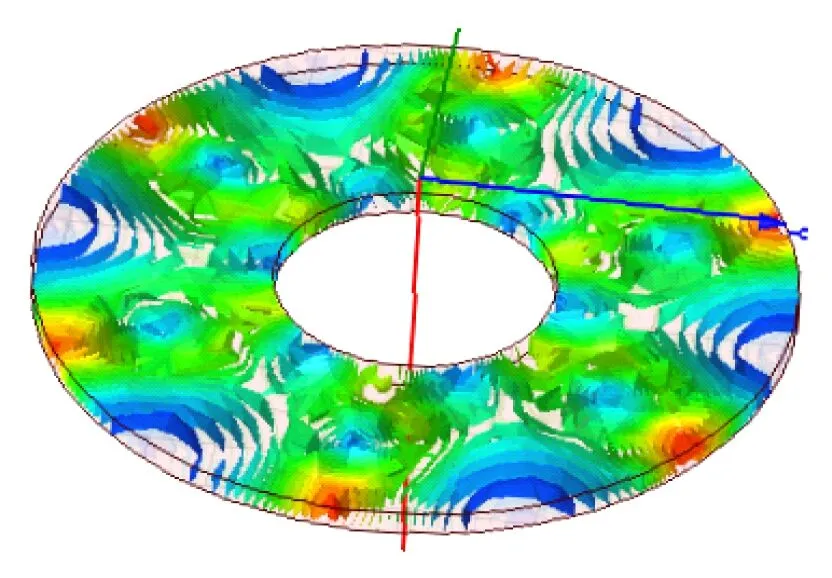
(c) 本文優化結果圖5 銅環渦流分布仿真圖

圖5(a)為采用文獻[18]優化方法的改進型HAPMC渦流分布；圖5(b)為采用文獻[19]的方法；圖5(c)為采用本文的優化方法。從圖5可以看出,本文設計的改進型HAPMC的渦流分布比較合理。

4.3.2 氣隙磁密波形畸變率仿真研究

分別對3種優化方法設計的改進型HAPMC進行氣隙磁密的仿真，并將仿真結果進行傅里葉分解，仿真位置為軸向氣隙與徑向氣隙的公共部分，圖6為文獻[18，19]和本文的仿真結果。

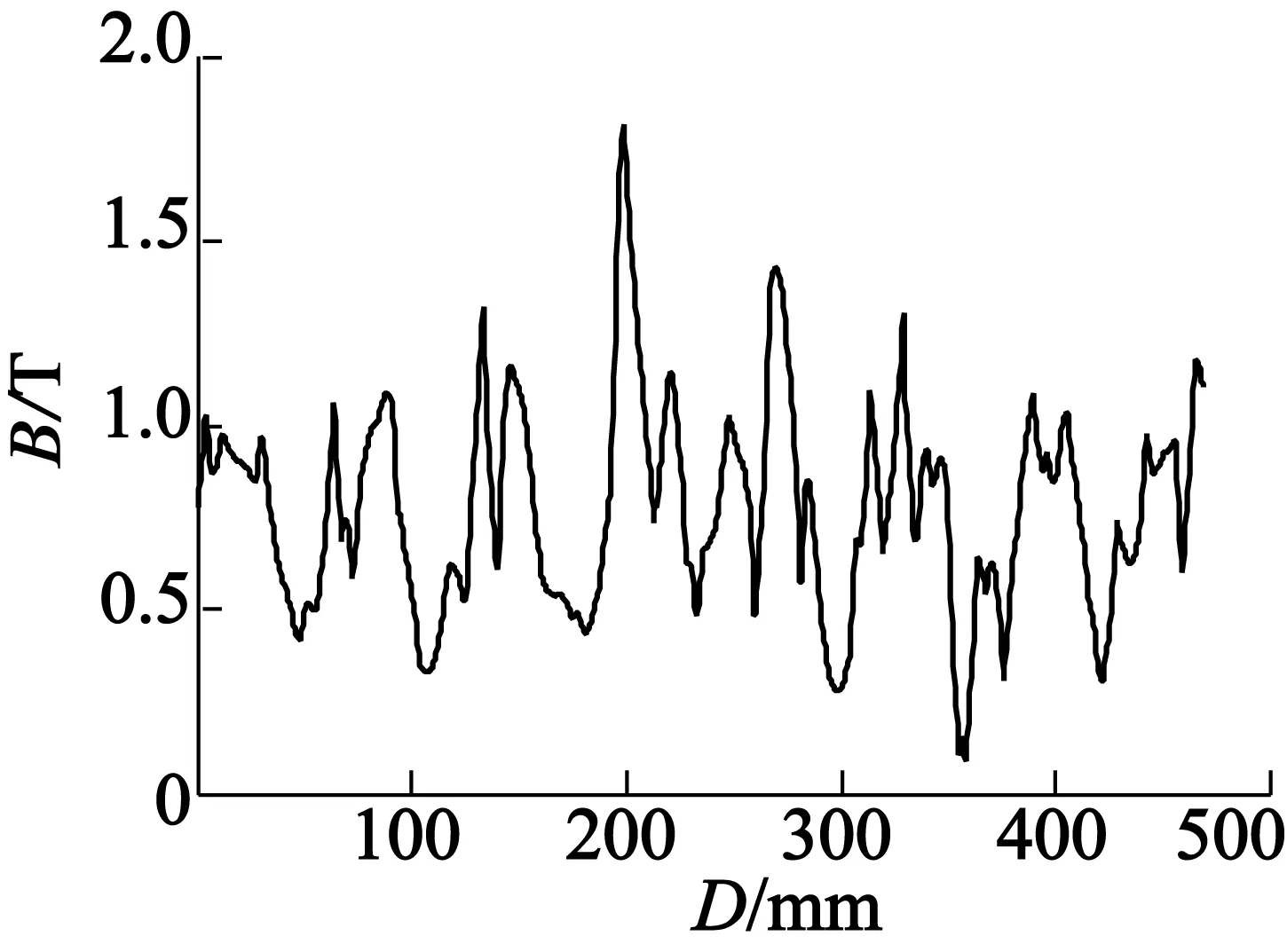
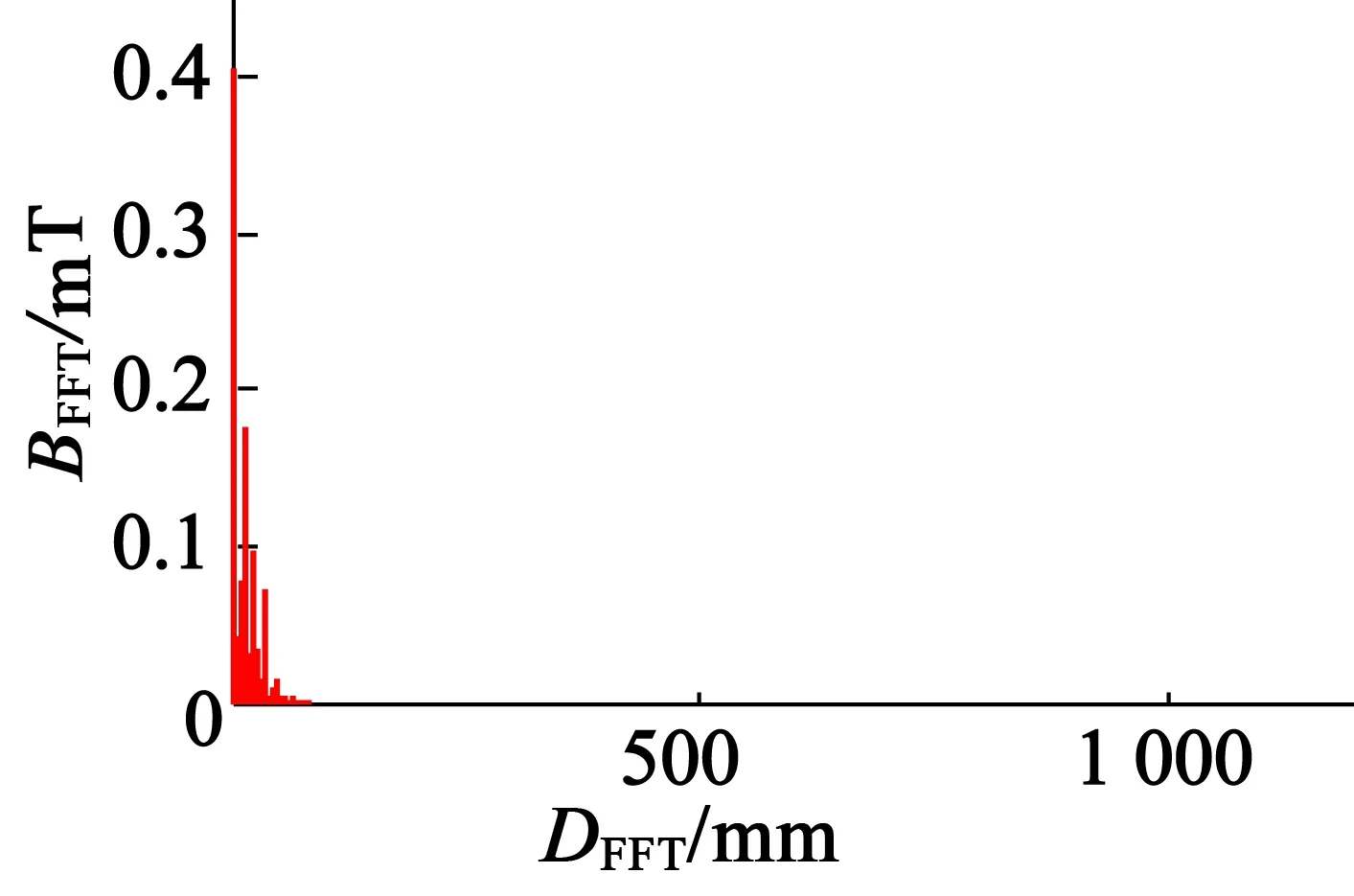
(a) 文獻[18]優化結果

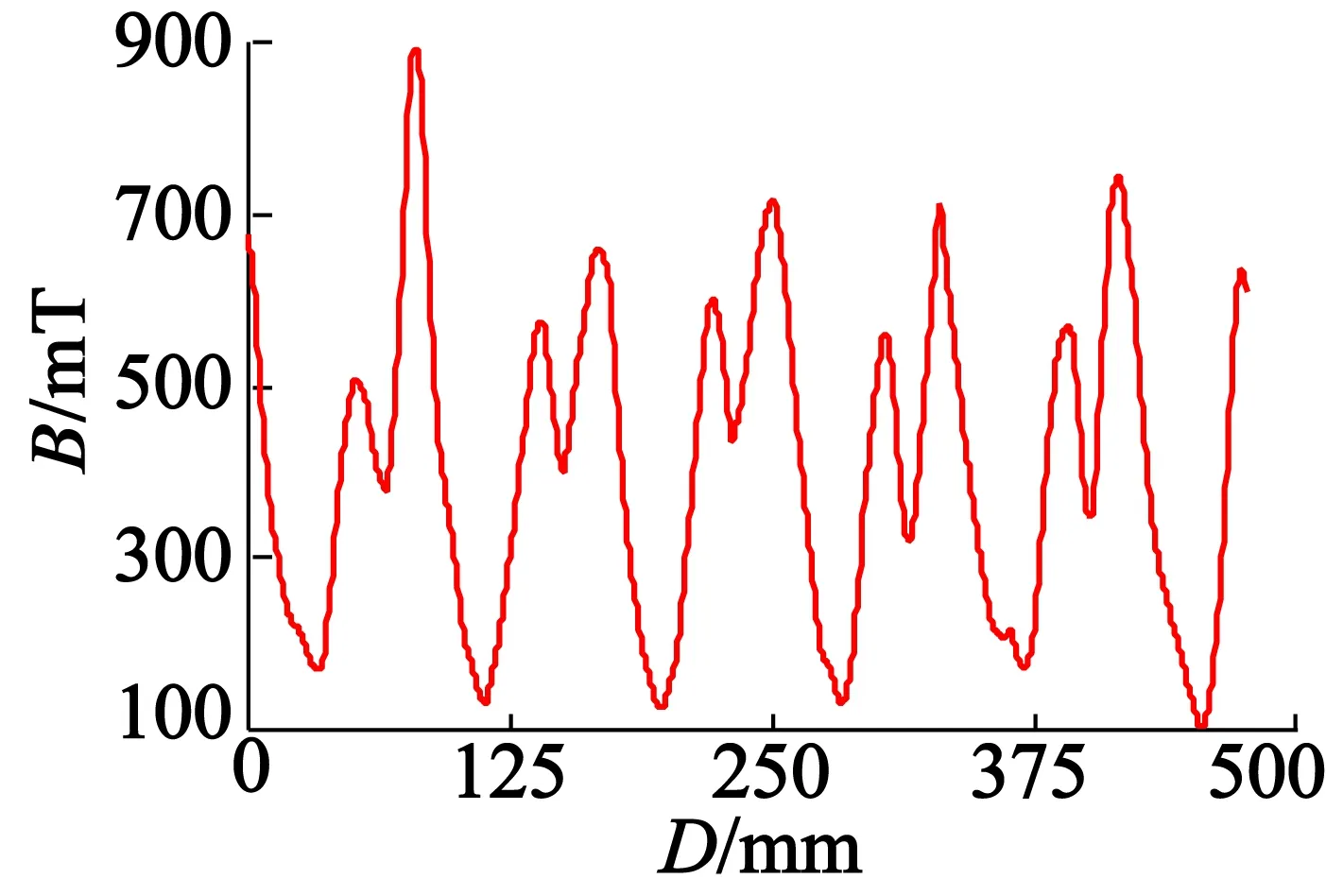
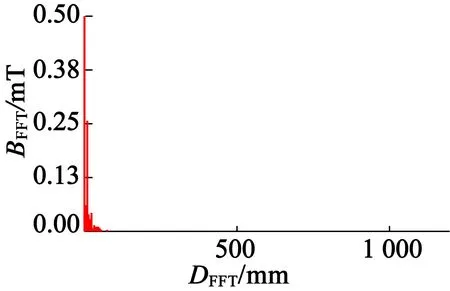
(b) 文獻[19]優化結果

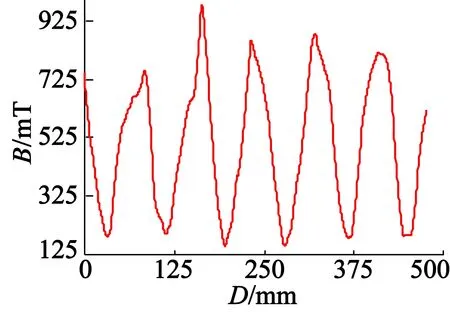
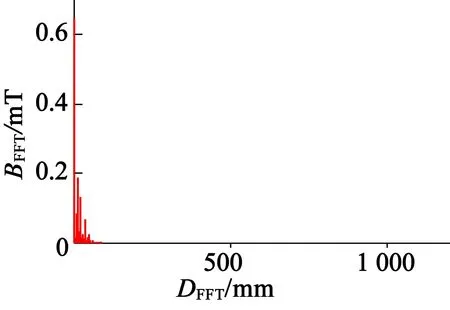
(c) 本文優化結果圖6 氣隙磁密仿真圖

從圖6氣隙磁密波形的仿真結果可以明顯看出，采用本文的優化方法設計的改進型HAPMC公共氣隙中諧波含量較少，這表明本文設計的改進型永磁轉子結構以及優化算法能夠有效削弱磁場的耦合。

4.3.3 輸出轉矩的仿真研究

圖7為3種優化設計的HAPMC的輸出轉矩仿真曲線。

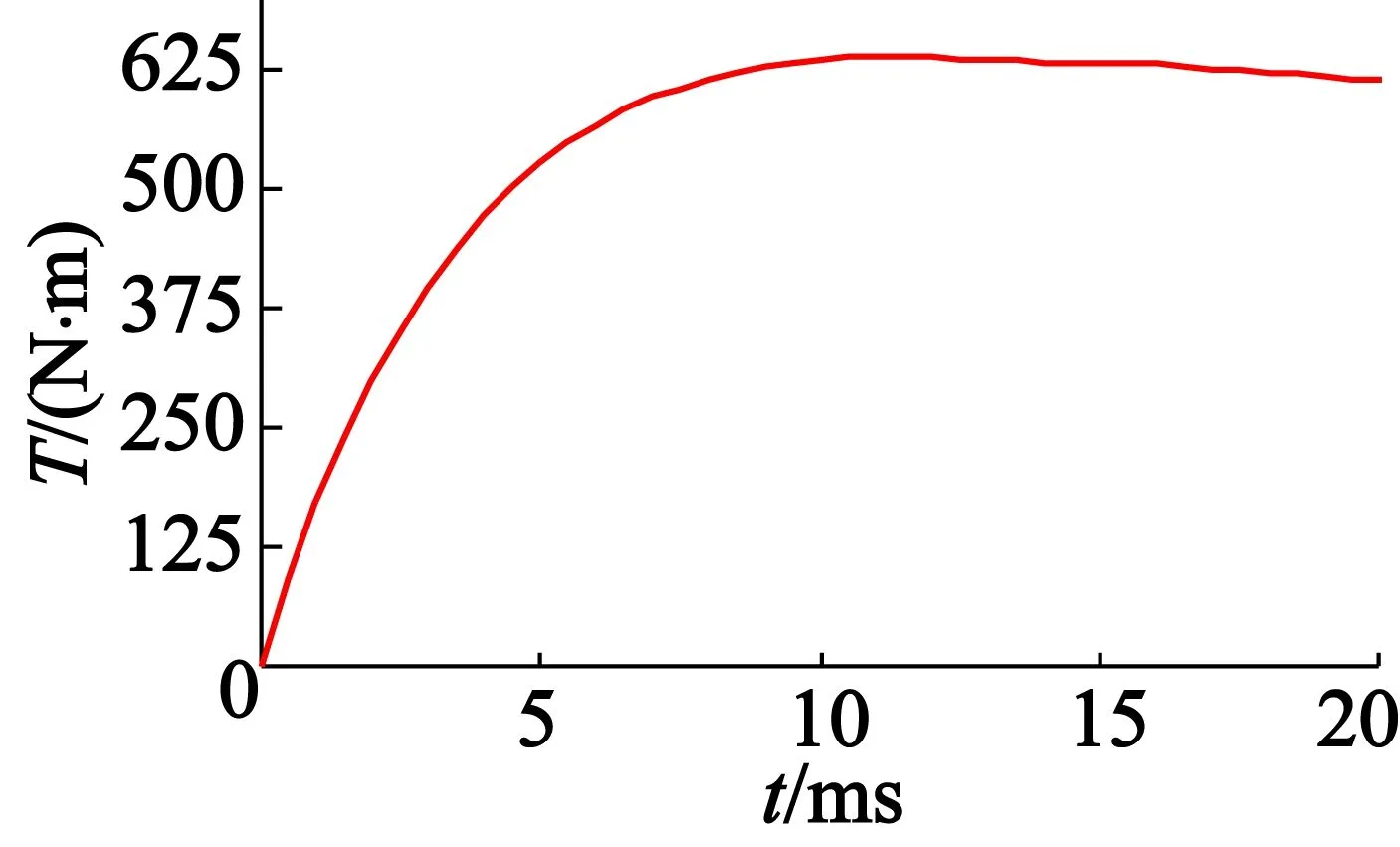
(a) 文獻[18]優化結果

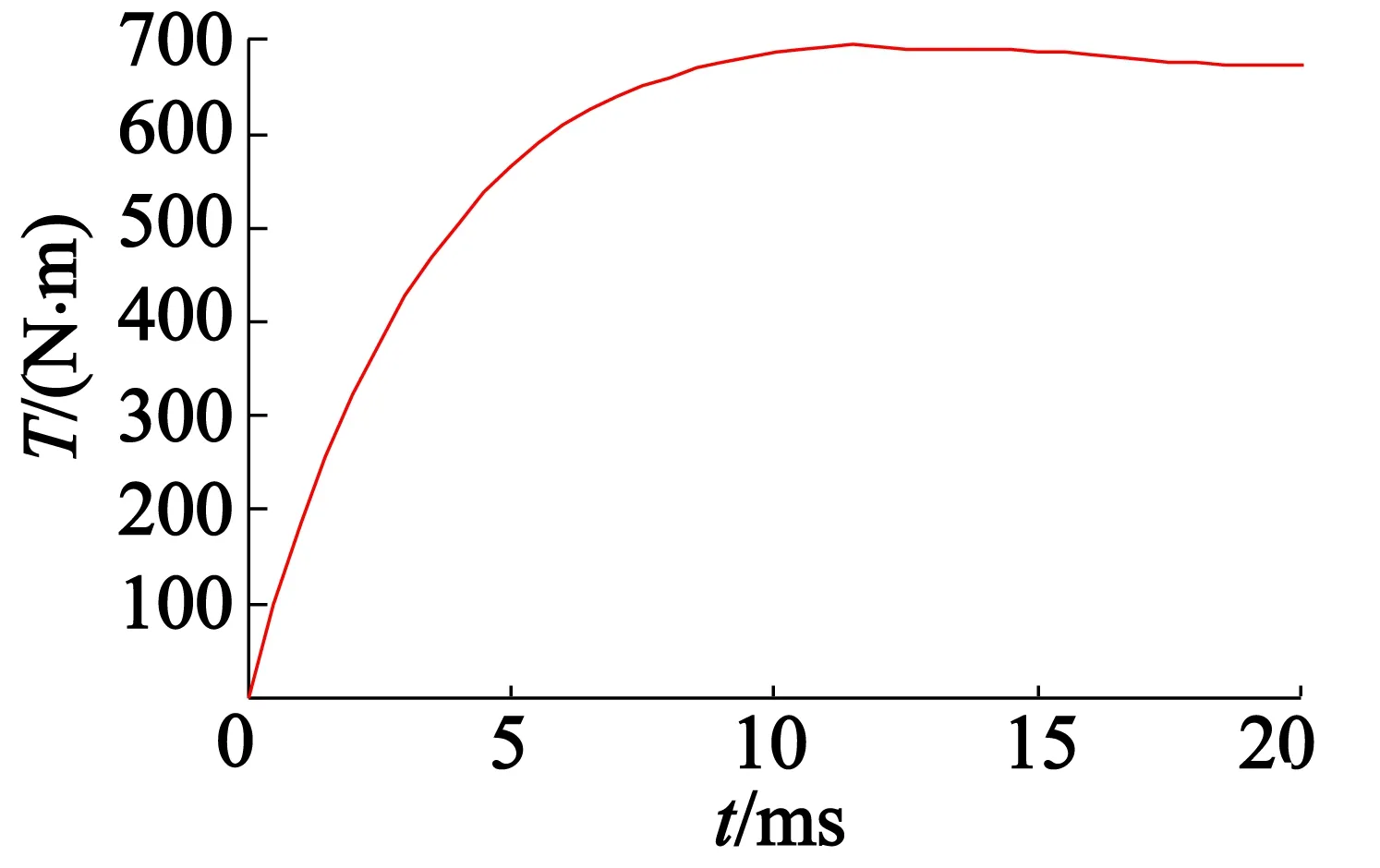
(b)文獻[19]優化結果

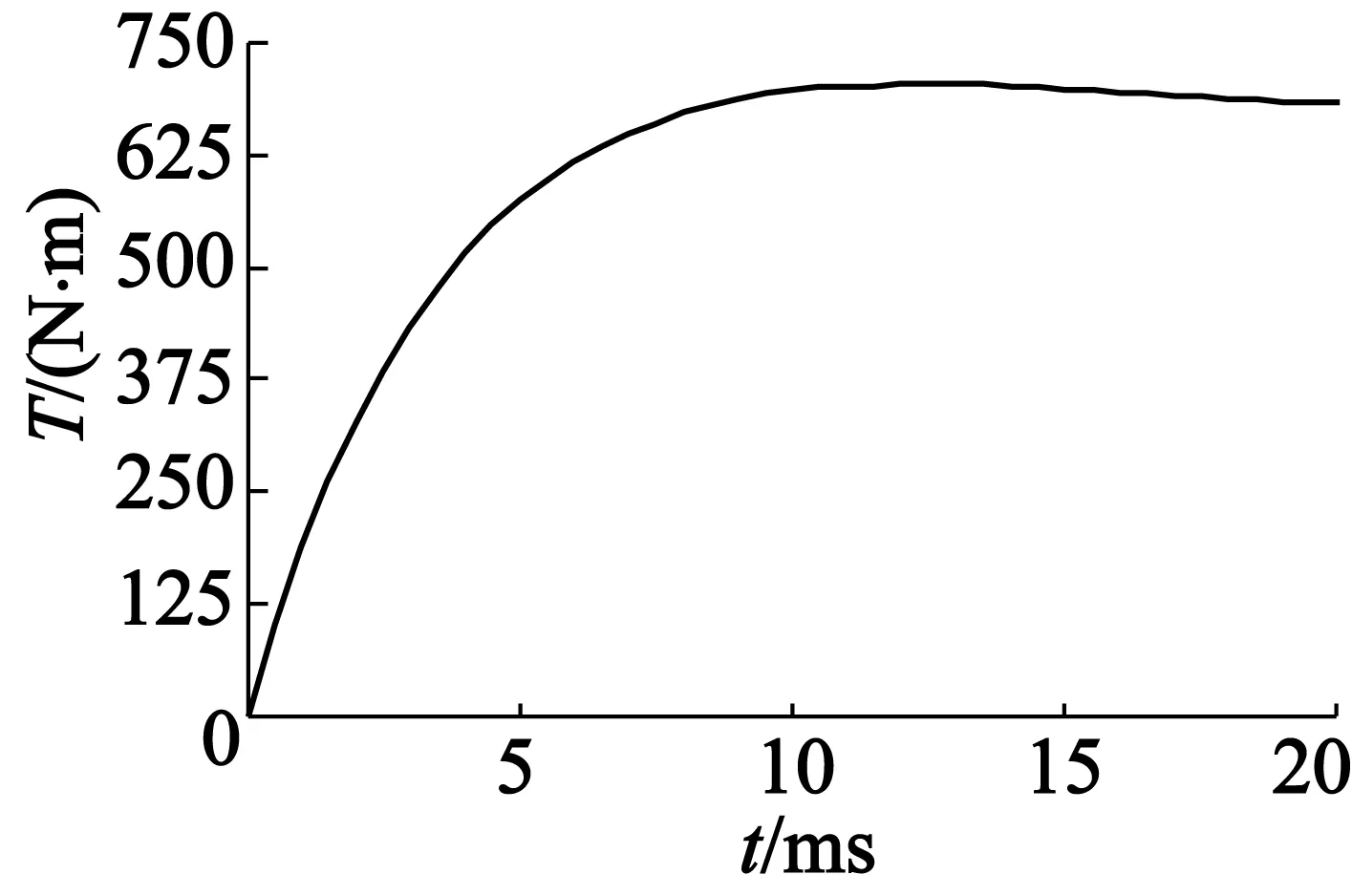
(c)本文優化結果圖7 輸出轉矩仿真圖

從圖7輸出轉矩的仿真結果可以明顯看出，采用本文優化方法設計的HAPMC輸出轉矩得到提高，這也間接說明了本文優化方法是可行的，有效的。

5 結 語

本文研究了一種新型結構的改進型HAPMC，選擇需要優化設計的參數并建立有限元仿真模型；采用面心立方設計進行試驗設計，確定訓練樣本；首次提出改進和聲搜索算法，并將之用于HAPMC預測模型的求解，得出了HAPMC的最優參數；最后，通過對比仿真驗證本文的優化設計方法可用于永磁調速器的設計并且效果較好，這也為其它耦合類傳動設備的優化設計提供了借鑒 。